2.5. The Applications of Quotient Space Theory
2.5.1. Introduction
In this section, we will present a new constructional definition of fuzzy sets by using fuzzy equivalence relations, and discuss its properties. We will also discuss the isomorphism and similarity principles of fuzzy sets, the necessary and sufficient condition of the isomorphism and ε-similarity of two fuzzy equivalence relations. These principles and results can overcome the subjectivity of the concept of fuzzy sets defined by membership functions to a certain extent, and deepen the understanding of fuzzy set theory so that a more objectively fuzzy set theory can be established probably. More details can be seen in (Zhang and Zhang, 2003b, 2003d, 2005b, 2005c).
Zadeh (1965) presented a fuzzy set theory that is an efficient tool for describing uncertainty, and has wide applications, for example, fuzzy control, fuzzy reasoning, etc. But the concept of fuzziness defined by membership functions that many people pay close attention to is subjective. The definition of fuzziness that Zadeh proposed is the following.
Definition 2.21
X is a domain. If 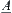 is a fuzzy subset of X, for any
is a fuzzy subset of X, for any 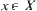 , assigning a number
, assigning a number  to x,
to x, 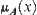 is called a membership of x with respect to
is called a membership of x with respect to 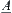 .
.
Mapping 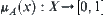 ,
, 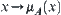 is called a membership function of
is called a membership function of 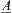 .
.
It is noted that in the following discussion, domain X is assumed to be infinite (not limited to finite). For simplicity, the membership function is denoted by 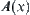 rather than
rather than 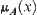 .
.
The main operations of fuzzy sets: given two fuzzy sets 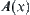 and
and 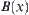 , the union, intersection, and complement operations are defined as follows:
, the union, intersection, and complement operations are defined as follows:
![]()
In practice such as fuzzy control, designers may choose the membership functions optionally in some degree, i.e., the membership functions of the same fuzzy variable may (slightly) be different, but the controllers designed from the different membership functions still have the same (or approximate) performances. The robustness of the fuzzy analysis method, based on (more or less) optionally chosen membership functions, has brought many people’s attention. Some researchers (Liang and Song, 1996; Lin and Tsumoto, 2000; Mitsuishi et al., 2000; Verkuilen, 2001; Lin, 2001a) presented the probabilistic interpretation of membership functions. For example, Lin (2001a) interpreted memberships as probabilities. Each sample space has a probability, and each point is associated with one sample space. So the total space is like a fiber space. Each fiber space is a probability space. Liang and Song (1996) regarded the values of a membership function as independent and identically distributed random variables, and proved that the mean of the membership function exists for all the elements of the universe of discourse. He interpreted the meaning of a subjective concept of a group of people as the mean of a membership function for all people within the group. Mitsuishi et al. (2000) introduced a new concept of empty fuzzy set, in order to define the membership functions in the probabilistic sense. That is, although different persons may assign (slightly) different membership functions to a fuzzy concept, when solving a real problem (fuzzy control or fuzzy reasoning), in average they can get an approximate result. Unfortunately, these results were obtained based on a strong assumption, i.e., the values of a membership function are assumed to be independent and identically distributed random variables. Verkuilen (2001) introduced the concept of membership functions by the multi-scale method, and discussed its corresponding properties. Lin (1988, 1992, 1997) presented a topological definition, topological rough set, of fuzzy sets by using neighborhood systems, discussed the properties of fuzzy sets from their structure, and then presented a definition of the equivalence between two fuzzy membership functions, and the necessary and sufficient conditions of the equivalence between two membership functions. He also discussed the concept of granular fuzzy sets in Lin (1998, 2001b), and ‘elastic’ membership functions in Lin (1996, 2000, 2001b). Lin’s works provide a structural interpretation of membership functions (fuzzy sets).
It can be seen that the membership function of a fuzzy set can be interpreted in two ways: one probabilistic, the other structural. We will show below that for a fuzzy set (concept), it may probably be described by different types of membership functions, as long as their structures (see the structural definition of fuzzy sets below) are the same, it still appears with the same characteristics. That is, although these membership functions are different in appearance, they are the same in essence. Therefore, the structural interpretation of fuzzy sets would be better than the probabilistic one. And it seems that in a given environment, most persons would have a similar structural interpretation for the same fuzzy concept. We will introduce a structural definition of fuzzy sets, and discuss its properties below, since the structural description is more essential to a fuzzy set.
2.5.2. The Structural Definition of Fuzzy Sets
2.5.2.1. The Structural Definition of Membership Functions
Definition 2.22
![]() (2.11)
(2.11)
A(x) is called a structural definition of membership functions.
Therefore, A is a fuzzy set extended from a crisp set A by fuzzy equivalence relation R and with A as its core. The new definition is induced from a fuzzy equivalence relation, and represents the relationship between a crisp set and its corresponding fuzzy set so that it deepens the understanding of fuzzy sets.
The following example shows that two different equivalence relations may correspond to the same hierarchical structure.
Example 2.16
Fuzzy equivalence relation 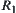 :
:  ,
, 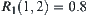 ,
, 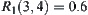 .
.
Its corresponding hierarchical structure is 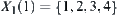 ,
, 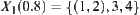 ,
, 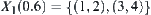 , and
, and 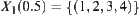 .
.
Fuzzy equivalence relation  is
is 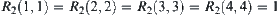 ,
, 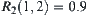 ,
, 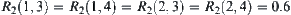 , and
, and 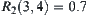 .
.
Its corresponding hierarchical structure is 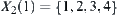 ,
,  ,
, 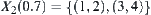 , and
, and 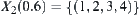 .
.
Fuzzy equivalence relations 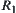 and
and 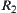 are different, but they have the same hierarchical structure {{1,2,3,4},{(1,2),3,4},{(1,2),(3,4)},{(1,2,3,4)}}. Certainly, there are countless fuzzy equivalence relations corresponding to the above hierarchical structure.
are different, but they have the same hierarchical structure {{1,2,3,4},{(1,2),3,4},{(1,2),(3,4)},{(1,2,3,4)}}. Certainly, there are countless fuzzy equivalence relations corresponding to the above hierarchical structure.
Definition 2.23
Definition 2.24
If 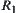 and
and 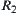 are two fuzzy equivalence relations corresponding to the same hierarchical structure, then
are two fuzzy equivalence relations corresponding to the same hierarchical structure, then 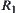 and
and 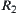 are called isomorphic.
are called isomorphic.
Definition 2.25
Given a fuzzy subset A and its membership function 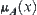 . Defining an equivalence relation
. Defining an equivalence relation 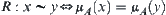 on X, we have a quotient space
on X, we have a quotient space  corresponding to R. Furthermore, define an order ‘<’ on
corresponding to R. Furthermore, define an order ‘<’ on 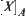 such that
such that 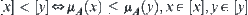 , space
, space 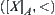 obtained is a totally ordered quotient space corresponding to fuzzy set A.
obtained is a totally ordered quotient space corresponding to fuzzy set A.
Definition 2.26
If two fuzzy subsets 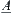 and
and 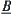 correspond to the same totally ordered quotient space, then
correspond to the same totally ordered quotient space, then 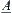 and
and  are called isomorphic.
are called isomorphic.
2.5.2.2. The Isomorphism Discrimination of Two Fuzzy Equivalence Relations
We will show below the properties of two equivalent fuzzy equivalence relations, and the necessary and sufficient condition of isomorphism for two fuzzy equivalence relations.
Proposition 2.14
If two fuzzy equivalence relations R1 and R2 on X are isomorphic, then we have the following properties.
1. For 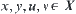 ,
, 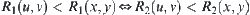 .
.
2. 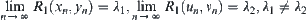
3. For  ,
, 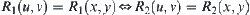 .
.
For simplicity, in the following discussion, we use the symbol 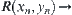 instead of
instead of 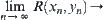 .
.
Proof:
1. Assume 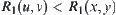 . Let
. Let 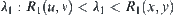 . f is an isomorphic mapping.
. f is an isomorphic mapping.
Since 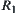 and
and 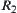 are isomorphic, there exists a one-one, strictly increasing, and onto mapping
are isomorphic, there exists a one-one, strictly increasing, and onto mapping 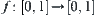 . Letting
. Letting 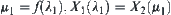 , we have x and y equivalent in
, we have x and y equivalent in 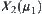 , but u and v are not equivalent in
, but u and v are not equivalent in 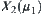 . Thus,
. Thus, 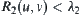 and
and 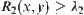 , i.e.,
, i.e., 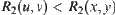 .
.
Similarly, we have 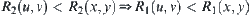 .
.
2. Let 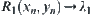 and
and 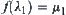 . We will show
. We will show 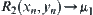 .
.
Otherwise, in assuming that 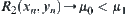 , for
, for 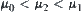 , let
, let 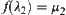 . Since f is a one-one, strictly increasing and onto mapping, we have
. Since f is a one-one, strictly increasing and onto mapping, we have 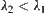 . In assuming
. In assuming 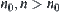 , we have
, we have 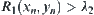 . Thus,
. Thus, 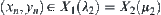 . Again, from
. Again, from 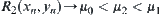 , we have
, we have 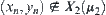 . This is a contradiction. So
. This is a contradiction. So 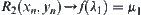 .
.
Since f is a one-one mapping, we have
![]()
![]()
3. Property 3 is the deduction of Property 1. Otherwise, there exist 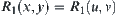 and
and 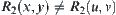 . But from Property 1, we have
. But from Property 1, we have 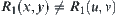 . This is a contradiction. So Property 3 holds.
. This is a contradiction. So Property 3 holds.
Definition 2.27
R1 and R2 are two fuzzy equivalence relations on X. Property 1 of Proposition 2.14 holds. Let 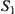 and
and 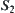 be the ranges of R1 and R2, respectively. Define
be the ranges of R1 and R2, respectively. Define  as
as 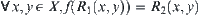 .
.
From Proposition 2.14, when Property 1 holds, Property 3 holds as well. From Definition 2.27, assume that 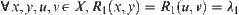 . From Property 3, we have
. From Property 3, we have 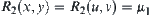 . Then,
. Then, 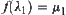 . Therefore, mapping f is defined as single valued and unique. From Property 1 of Proposition 2.14, f is a one-one and strictly increasing.
. Therefore, mapping f is defined as single valued and unique. From Property 1 of Proposition 2.14, f is a one-one and strictly increasing.
Proposition 2.15
R1 and R2 are two fuzzy equivalence relations on X, and satisfy Property 1 of Proposition 2.14. Let 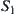 and
and 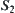 be the ranges of R1 and R2, respectively. Then, the mapping f defined by Definition 2.27 can be extended to a one-one, strictly increasing, and onto mapping from
be the ranges of R1 and R2, respectively. Then, the mapping f defined by Definition 2.27 can be extended to a one-one, strictly increasing, and onto mapping from 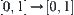 .
.
Proof:
Letting 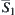 and
and 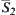 are closures of
are closures of 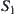 and
and 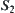 , respectively, set
, respectively, set 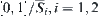 , is open and may be represented by the union of at most countable many open intervals. Their starting and finishing points are
, is open and may be represented by the union of at most countable many open intervals. Their starting and finishing points are 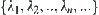 and
and 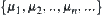 , respectively.
, respectively.
For any 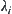 , there exists
, there exists 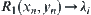 . Define
. Define 
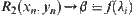 .
.
We will show next that 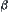 must be some
must be some 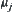 .
.
Otherwise, in assuming that 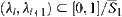 , there exists
, there exists 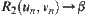 (monotonously decrease to
(monotonously decrease to 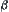 ). From Property 1 and 2, we have
). From Property 1 and 2, we have 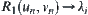 (monotonously decrease to
(monotonously decrease to 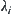 ). Then there exists
). Then there exists 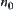 , when
, when 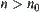 ,
, 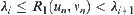 .
.
This contradict with 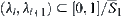 . Then, we have that
. Then, we have that 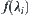 is some
is some 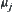 .
.
Similarly, when 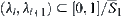 , we have
, we have 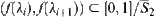 .
.
Now, f will be expanded to [0,1]. For  , let
, let 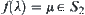 . When
. When 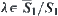 let
let 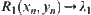 . And let
. And let 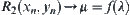 . When
. When 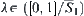 assume that
assume that 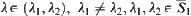 . Letting
. Letting 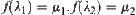 we have
we have 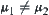 . When
. When 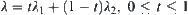 define
define 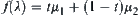 .
.
Therefore, f is expanded to a one-one, strictly increasing, and onto mapping from 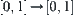 .
.
Assume that 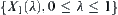 and
and 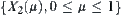 are hierarchical structures corresponding to
are hierarchical structures corresponding to 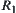 and
and 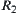 , respectively, then
, respectively, then 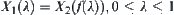 .
.
Theorem 2.7: The Discrimination Principle of Isomorphism
R1 and R2 are two fuzzy equivalence relations on X. The necessary and sufficient conditions of isomorphism of R1 and R2 are that the following two properties hold.
1. Property 1 of Proposition 2.14
2. Property 2 of Proposition 2.14
Proof:
The expansion process is the following.
From Property 2 of Proposition 2.14, for point  , let
, let  . Letting
. Letting 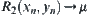 , we define
, we define  . For
. For 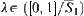 , i.e.,
, i.e., 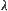 is an external point of S, there exists an interval
is an external point of S, there exists an interval  such that
such that 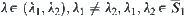 .
.
Letting 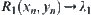 and
and  , we have
, we have
![]()
Letting 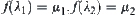 , and
, and 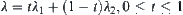 , define
, define 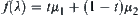 .
.
Therefore, f is expanded to a one-one, strictly increasing, and onto mapping from 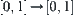 , i.e., an isomorphic mapping corresponding to R1 and R2.
, i.e., an isomorphic mapping corresponding to R1 and R2.
Proposition 2.16
The ranges of R1 and R2 are [0,1]. The isomorphism of R1 and R2 ⇔ their corresponding function  is a strictly increasing and continuous function.
is a strictly increasing and continuous function.
Proof:
⇐: Since f is a strictly increasing and continuous function, for any  , and Property 2 of Proposition 2.14 holds. From Proposition 2.15, R1 and R2 are isomorphic.
, and Property 2 of Proposition 2.14 holds. From Proposition 2.15, R1 and R2 are isomorphic.
⇒: Assume that R1 and R2 are isomorphic. From the Basic Theorem, it’s known that their corresponding isomorphic mapping 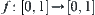 is a one-one, strictly increasing, and onto mapping. So f is continuous.
is a one-one, strictly increasing, and onto mapping. So f is continuous.
Corollary 2.2
Assume  is a distance function on
is a distance function on  . Two fuzzy equivalence relations on X are defined as follows.
. Two fuzzy equivalence relations on X are defined as follows.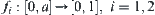 are strictly decreasing and continuous functions. Then, R1 and R2 are isomorphic.
are strictly decreasing and continuous functions. Then, R1 and R2 are isomorphic.
![]()
Proof:
We have 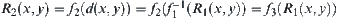 , where
, where  , and
, and 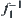 is the inverse of
is the inverse of 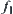 . Since
. Since 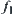 and
and 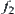 are strictly decreasing and continuous,
are strictly decreasing and continuous, 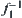 is also strictly decreasing and continuous. Since
is also strictly decreasing and continuous. Since 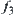 is the combination of two strictly decreasing and continuous functions,
is the combination of two strictly decreasing and continuous functions, 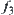 is strictly increasing and continuous. Then, we have that R1 and R2 are isomorphic.
is strictly increasing and continuous. Then, we have that R1 and R2 are isomorphic.
Corollary 2.3
Assume 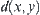 is a distance function on
is a distance function on 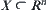 . Two fuzzy equivalence relations on X are defined as follows.
. Two fuzzy equivalence relations on X are defined as follows.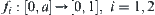 .
.
![]()
If  , then R1 and R2 are isomorphic.
, then R1 and R2 are isomorphic.
Example 2.17
Assume 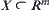 . Let
. Let
![]()
![]()
Choose a proper 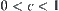 such that
such that  .
.
![]()
We have 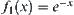 ,
, 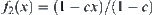 ,
, 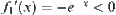 , and
, and 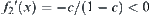 . From Corollary 2.3, R1 and R2 are isomorphic.
. From Corollary 2.3, R1 and R2 are isomorphic.
2.5.3. The Robustness of the Structural Definition of Fuzzy Sets
2.5.3.1. The Isomorphism of Fuzzy Sets
Proposition 2.17
R1 and R2 are two isomorphic fuzzy equivalence relations on X. f is isomorphic transformation. A is a common set on X. For 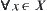 , fuzzy subsets
, fuzzy subsets 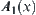 and
and 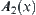 are defined by
are defined by  and
and 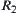 , according to Definition 2.22. Then,
, according to Definition 2.22. Then,  and
and 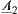 are isomorphic, and
are isomorphic, and 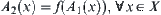 .
.
Proof:
From Definition 2.22, we have
![]()
From 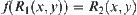 and that f is one-one and strictly increasing, there exists
and that f is one-one and strictly increasing, there exists 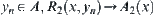 such that
such that
![]()
Again, sine f is strictly increasing and continuous, we have  . Thus,
. Thus,  and
and 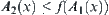 .
.
Similarly, we have  , i.e.,
, i.e., 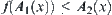
Finally, 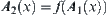 .
.
Proposition 2.18
R1 and R2 are two isomorphic fuzzy equivalence relations on X. A and B are two common sets on X. Fuzzy subsets  and
and  are defined by
are defined by 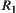 and
and 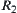 , according to Definition 2.22. Then,
, according to Definition 2.22. Then, 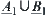 and
and 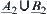 (or
(or 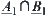 and
and 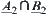 ) are isomorphic.
) are isomorphic.
Proof:
In order to show that 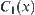 and
and 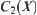 are isomorphic, it is only needed to show
are isomorphic, it is only needed to show 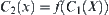 ,
, 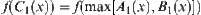 . Since f is one-one and strictly increasing, from Proposition 2.15, we have
. Since f is one-one and strictly increasing, from Proposition 2.15, we have
![]()
Therefore, 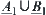 and
and  are isomorphic.
are isomorphic.
Similarly, 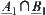 and
and 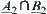 are isomorphic.
are isomorphic.
Proposition 2.19
R1 and R2 are two isomorphic fuzzy equivalence relations on X. A and B are two common sets on X. Fuzzy subsets 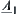 and
and 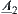 are defined by
are defined by 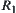 and
and 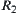 , according to Definition 2.22, then
, according to Definition 2.22, then 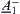 and
and 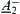 are isomorphic, where
are isomorphic, where 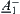 is the complement of A1, and its membership function is
is the complement of A1, and its membership function is 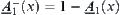 .
.
Proof:
Since the corresponding totally ordered quotient space of the complement of  has the same elements with that of
has the same elements with that of  and the only difference is their opposite order,
and the only difference is their opposite order, 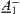 and
and 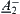 are isomorphic.
are isomorphic.
Theorem 2.8: Isomorphism Principle
R1 and R2 are two isomorphic fuzzy equivalence relations, and 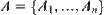 is a set of common subsets on X. Define two sets
is a set of common subsets on X. Define two sets 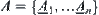 and
and 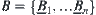 of fuzzy subsets from
of fuzzy subsets from 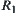 and
and 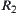 respectively, and carry out a finite number of union, intersection and complement operations on them, we have two sets
respectively, and carry out a finite number of union, intersection and complement operations on them, we have two sets 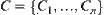 and
and 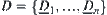 of fuzzy subsets. Then, the two sets C and D of fuzzy sets are isomorphic.
of fuzzy subsets. Then, the two sets C and D of fuzzy sets are isomorphic.
Proof:
The conclusion can be obtained from Propositions 2.15 and 2.16.
The theorem shows that the corresponding totally ordered quotient space of a fuzzy subset is its essential property. For the isomorphic fuzzy subsets, although they might have different membership functions, after a finite number of operations (inference), the fuzzy subsets obtained are still isomorphic. Therefore, as long as the essential property of fuzzy subsets remains the same, the usage of different membership functions does not affect the final results.
Example 2.18
Define fuzzy subsets 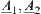 and
and 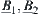 from
from 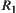 and
and 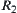 , respectively. Their membership functions as follows.
, respectively. Their membership functions as follows.
![]()
Then we have
![]()
Fuzzy sets 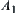 and
and 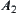 have different membership functions on X, but they are isomorphic since they correspond to the same totally ordered quotient space
have different membership functions on X, but they are isomorphic since they correspond to the same totally ordered quotient space 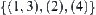 .
.
Similarly, fuzzy sets 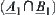 and
and 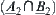 also have different membership functions, but they correspond to the same totally ordered quotient space
also have different membership functions, but they correspond to the same totally ordered quotient space 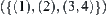 as well.
as well.
From the structural relation view point, both fuzzy subsets 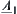 and
and 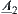 indicate that elements 1 and 3 belong to their core A, and element 2 is closer to the core than element 4. Due to the different understanding of each person, their descriptions of the degree of closeness might be different, but the mutual relationships among elements should be the same.
indicate that elements 1 and 3 belong to their core A, and element 2 is closer to the core than element 4. Due to the different understanding of each person, their descriptions of the degree of closeness might be different, but the mutual relationships among elements should be the same.
The structural definition, given in Definition 2.22, of fuzzy sets is defined from fuzzy equivalence relations. This is very significant. For example, if using neighborhood systems to defined fuzzy sets directly, the isomorphism principle might not hold. The following is a counter-example.
Example 2.19
Assume that the structures of fuzzy subsets 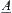 and
and 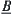 are the following.
are the following.
![]()
Define their membership functions as follows
Carry out set operations on 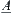 and
and 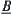 with membership functions
with membership functions 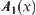 ,
, 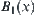 and
and 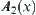 ,
, 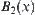 , respectively, we have
, respectively, we have
![]()
After the set operations, the results with respect to different membership functions are no long isomorphic. This shows that using fuzzy membership functions to define fuzzy sets, although it is a structural definition but cannot satisfy the isomorphism principle generally (Lin, 1997).
2.5.3.2. The  -Similarity of Fuzzy Sets
-Similarity of Fuzzy Sets
The Definition of  -Similarity of Fuzzy Sets
-Similarity of Fuzzy Sets
In the above section, we presented a structural definition of fuzzy sets, which answers the cause of the robustness of fuzzy analysis in some degree. But the conditions that two fuzzy equivalence relations are isomorphic are too strong. We present a weaker condition, i.e.,  -similarity of fuzzy sets, below.
-similarity of fuzzy sets, below.
Definition 2.28
Given two fuzzy equivalence relations 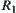 and
and 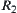 , and
, and 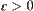 . If there exists fuzzy equivalence relation
. If there exists fuzzy equivalence relation 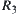 such that (1)
such that (1) 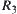 and
and 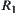 are isomorphic, (2)
are isomorphic, (2)  , then
, then 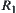 and
and 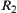 are called
are called  -similarity.
-similarity.
Definition 2.29
Given two fuzzy equivalence relations  and
and 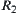 , and
, and 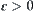 . If there exists fuzzy set
. If there exists fuzzy set 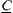 such that (1)
such that (1) 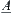 and
and 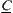 are isomorphic (or
are isomorphic (or 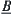 and
and 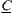 are isomorphic), (2)
are isomorphic), (2) 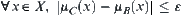 (or
(or 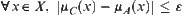 ), then
), then 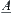 and
and 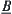 are called
are called  -similarity.
-similarity.
Proposition 2.20
Assume that 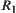 and
and 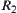 are two
are two  -similarity fuzzy equivalence relations on X. A is a common set on X. Fuzzy subsets
-similarity fuzzy equivalence relations on X. A is a common set on X. Fuzzy subsets 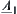 and
and 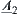 are defined by
are defined by  and
and 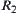 , respectively, according to Definition 2.22, then
, respectively, according to Definition 2.22, then 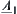 and
and 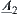 are called
are called  -similarity.
-similarity.
Proof:
Assume that 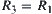 , i.e.,
, i.e., 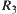 and
and 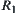 are isomorphic, and
are isomorphic, and 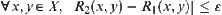 .
.
For x, assume that 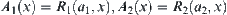 . Thus
. Thus
![]()
Similarly, 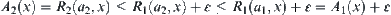 .
.
That is, 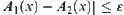 . We have that
. We have that  and
and 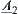 are
are  -similarity.
-similarity.
Proposition 2.21
Assume that 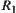 and
and 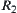 are two
are two  -similarity fuzzy equivalence relations on X. A and B are two common sets on X. Fuzzy subsets
-similarity fuzzy equivalence relations on X. A and B are two common sets on X. Fuzzy subsets 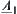 ,
,  and
and 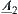 ,
, 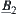 are defined from
are defined from 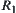 and
and 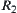 , according to Definition 2.22. Then,
, according to Definition 2.22. Then, 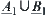 and
and 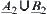 (or
(or 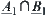 and
and 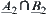 ) are
) are  -similarity.
-similarity.
Proof:
The membership functions corresponding to the four fuzzy sets are 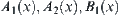 and
and 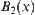 , respectively. The membership functions of
, respectively. The membership functions of 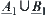 and
and 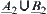 are denoted by
are denoted by 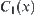 and
and 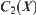 , respectively. From Definition 2.22,
, respectively. From Definition 2.22,
![]()
Assume that 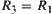 , i.e.,
, i.e.,  and
and  are isomorphic, and
are isomorphic, and 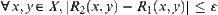 .
.
Assume that 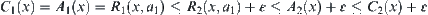 .
.
Similarly, 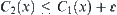 . Finally, we have
. Finally, we have 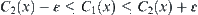 , i.e.,
, i.e., 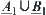 and
and 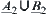 are
are  -similarity.
-similarity.
Similarly, 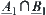 and
and 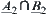 are
are  -similarity.
-similarity.
Theorem 2.9: Similarity Principle
Proof:
Assume that  and
and 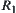 are isomorphic, and
are isomorphic, and 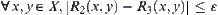 . Let
. Let  be a set of fuzzy sets defined by
be a set of fuzzy sets defined by 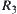 . After a finite number of set operations, we have a set
. After a finite number of set operations, we have a set 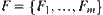 of fuzzy sets. From the isomorphism principle, C and F are isomorphic.
of fuzzy sets. From the isomorphism principle, C and F are isomorphic.
On the other hand, using the same method of Proposition 2.21, we have  , i.e., D and C are
, i.e., D and C are  -similarity, where
-similarity, where 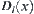 and
and  are membership functions of fuzzy sets
are membership functions of fuzzy sets 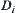 and
and  .
.
The Discrimination of  -Similarity of Fuzzy Sets
-Similarity of Fuzzy Sets
Theorem 2.10
Assume that the ranges of 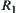 and
and 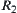 are [0,1]. Then, we have
are [0,1]. Then, we have 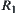 and
and 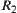 are
are  -similarity ⇔ there exists a strictly increasing function F such that
-similarity ⇔ there exists a strictly increasing function F such that 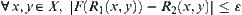 .
.
Proof:
Let  . From Proposition 2.16, we have
. From Proposition 2.16, we have 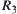 and
and 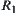 are isomorphic. Then, from Definition 2.28, we have
are isomorphic. Then, from Definition 2.28, we have 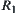 and
and 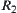 are
are  -similarity.
-similarity.
3. The Structural Property of  -Similarity of Fuzzy Equivalence Relations
-Similarity of Fuzzy Equivalence Relations
Assume that 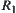 and
and 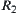 are two equivalence relations.
are two equivalence relations. 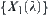 and
and 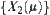 are their corresponding hierarchical structures. If
are their corresponding hierarchical structures. If 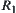 and
and 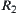 are
are  -similarity, then there exists a strictly increasing function
-similarity, then there exists a strictly increasing function 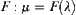 for
for 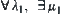 such that
such that 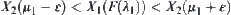 .
.
Conversely, for 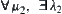 such that
such that  .
.
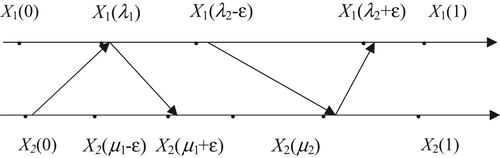
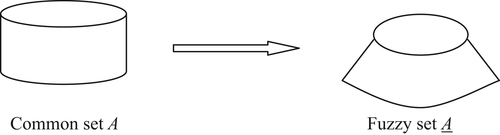
Fig. 2.3 shows that the hierarchical structures corresponding to 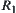 and
and 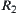 cannot be merged into one structure, but for any quotient space
cannot be merged into one structure, but for any quotient space 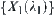 within
within 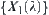 , there exist two quotient spaces
, there exist two quotient spaces 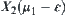 and
and  in
in 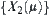 , one is in front of
, one is in front of 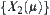 , and the other is behind
, and the other is behind 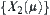 . Conversely, for any
. Conversely, for any 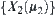 within
within 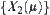 , there exist two quotient spaces
, there exist two quotient spaces 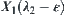 and
and  in
in 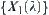 , one is in front of
, one is in front of 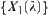 , and the other is behind
, and the other is behind 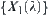 .
.
2.5.3.3. The Geometrical Meaning of the Structural Definition of Fuzzy Sets
In the structural definition of fuzzy sets, their membership functions are induced from equivalence relations. Now, we discuss the geometrical meaning of structures of fuzzy sets by using structures of fuzzy equivalence relations.
A fuzzy equivalence relation 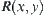 is given. First, assume that fuzzy subset
is given. First, assume that fuzzy subset 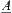 is induced from a singleton
is induced from a singleton 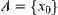 . The membership function of the fuzzy set defined by
. The membership function of the fuzzy set defined by 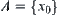 is
is 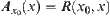 . From Basic Theorem, letting
. From Basic Theorem, letting 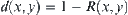 , then
, then  is a normalized isosceles distance of some quotient space [X] of X. Under the distance,
is a normalized isosceles distance of some quotient space [X] of X. Under the distance,  is the neighborhood system of
is the neighborhood system of 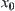 , where
, where 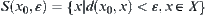 corresponds to the structure of fuzzy set
corresponds to the structure of fuzzy set 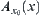 .
.
According to Definition 2.25, a totally ordered quotient space 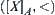 can be defined by the neighborhood system. The order of the quotient space is decided by the distance from point
can be defined by the neighborhood system. The order of the quotient space is decided by the distance from point 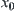 .
.
Generally, for any set A, define a fuzzy set A based on Definition 2.22, and A(x) is its membership function. Letting 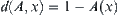 ,
, 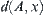 is the distance from point x to set A in the sense of distance
is the distance from point x to set A in the sense of distance 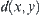 . If
. If 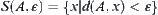 is a ε-neighborhood of A, then a corresponding totally ordered quotient space can be defined by the neighborhood system
is a ε-neighborhood of A, then a corresponding totally ordered quotient space can be defined by the neighborhood system 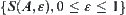 of A, according to Definition 2.25, where the order of the quotient space is decided by the distance from a point to set A.
of A, according to Definition 2.25, where the order of the quotient space is decided by the distance from a point to set A.
From the isomorphism principle in Section 2.5.2, it’s known that the structure of the totally ordered quotient space, corresponding to a fuzzy subset, is the essential property of the fuzzy subset.
Fig. 2.4 shows the geometrical intuition of common set A, and its corresponding fuzzy set A, where a crisp set A corresponds to a ‘platform’ with a vertical boundary face, while a fuzzy set A corresponds to a ‘platform’ with a slant boundary face.
From Definition 2.25, it’s known that a fuzzy set A decides an order relation of some quotient space [X] on X. The order is the essential property of A, and provides the relationship of distances from a spatial point to the core  of fuzzy set A. In common membership functions, an absolute value is used to describe the relation between a fuzzy set and any element within the set. While in the structural definition of fuzzy sets, the relative order relationship among elements is used to describe the fuzziness. Using the structural definition, as long as people have the same understanding of the relative order relation (or
of fuzzy set A. In common membership functions, an absolute value is used to describe the relation between a fuzzy set and any element within the set. While in the structural definition of fuzzy sets, the relative order relationship among elements is used to describe the fuzziness. Using the structural definition, as long as people have the same understanding of the relative order relation (or  -similarity) among elements, even different membership functions are used, the results they have are isomorphic (
-similarity) among elements, even different membership functions are used, the results they have are isomorphic ( -similarity), and after a finite number of fuzzy set operations, the results are still isomorphic. We show an example below.
-similarity), and after a finite number of fuzzy set operations, the results are still isomorphic. We show an example below.
Example 2.20
Fuzzy equivalence relation 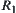 is as Example 2.16. Letting
is as Example 2.16. Letting 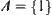 , define A and its corresponding membership function as
, define A and its corresponding membership function as
![]()
Its corresponding totally ordered quotient space is {(1),(1,2),(1,2,3,4)}.
Letting  be
be 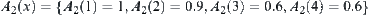 , then its corresponding totally ordered quotient space is {(1),(1,2),(1,2,3,4)}.
, then its corresponding totally ordered quotient space is {(1),(1,2),(1,2,3,4)}.
There are three elements (1),(2),(3,4) in quotient space [X]A. Their order relation is (1)<(2)<(3,4). And the order relation is the essential property of fuzzy set 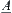 .
.
2.5.4. Conclusions
In the section, from the quotient space theory, we present the structural definition of a fuzzy set based on fuzzy equivalence relations, and the isomorphism and similarity principles of fuzzy sets. These principles may interpret the cause of robustness of fuzzy analysis, and answer the question why the same (or similar) results can be had, even using different membership functions in real fuzzy analysis.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
