5.4. Dimension Reduction Method
The RMG of moving object A among obstacles is usually high-dimensional. The judgment of the connectivity of 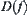 is rather difficult when the environment of A is cluttered up with obstacles. Based on the multi-granular computing strategy, we may observe the connectivity of the high-dimensional graph from its quotient space, if the connectivity is preserved in that space. Since the quotient space is simpler than the original one generally, this will make the complexity reduced.
is rather difficult when the environment of A is cluttered up with obstacles. Based on the multi-granular computing strategy, we may observe the connectivity of the high-dimensional graph from its quotient space, if the connectivity is preserved in that space. Since the quotient space is simpler than the original one generally, this will make the complexity reduced.
Based on the basic idea above, we present a dimension reduction method for investigating the connectivity of high-dimensional graph. Roughly speaking, if E is a subset in a high-dimensional space 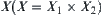 there exists a unique mapping
there exists a unique mapping  such that
such that 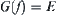 . If f satisfies certain conditions, the connectivity of E can be inferred from the connectivity of the domain
. If f satisfies certain conditions, the connectivity of E can be inferred from the connectivity of the domain 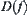 of f and
of f and  . This is called a dimension reduction method.
. This is called a dimension reduction method.
5.4.1. Basic Principle
We now use some topologic terminologies and techniques to show the basic theorems of the dimension reduction method. Readers who are not familiar with the contents are referred to Eisenberg (1974) and Sims (1976).
The mappings discussed in point set topology are usually single-valued. But the mappings concerned here are multi-valued. It is necessary to extend some concepts of topology to the multi-valued mappings.
For simplicity, the spaces addressed here are assumed to be metric spaces.
Definition 5.11
Definition 5.12
If  is semi-continuous at any point of
is semi-continuous at any point of 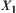 , then
, then  is semi-continuous on
is semi-continuous on 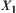 .
.
Definition 5.13
Definition 5.14
F is a mapping from 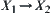 and is called a union mapping of
and is called a union mapping of 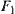 and
and 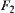 .
.
Theorem 5.2
Proof
Assuming that 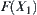 is not connected, then
is not connected, then 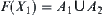 , where
, where  and
and  are mutually disjoint non-empty open sets. Let
are mutually disjoint non-empty open sets. Let
![]()
Since 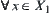 ,
,  is connected and sets
is connected and sets  and
and  are separated, then either
are separated, then either 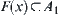 or
or  holds. We assume that
holds. We assume that 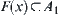 .
.
For any 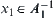 , there exists
, there exists 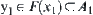 . Let
. Let  . Since
. Since  is open,
is open,  is a neighborhood of
is a neighborhood of 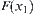 .
.
From the semi-continuity of F, for 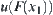 there exists a
there exists a 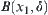 such that when
such that when 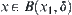 ,
, 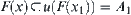 holds. Namely,
holds. Namely, 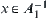 . We have
. We have 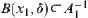 . Thus,
. Thus, 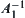 is open.
is open.
Similarly, 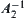 is also open.
is also open.
Finally, we show that  must hold. Otherwise, there exists
must hold. Otherwise, there exists 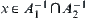 , that is,
, that is, 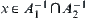 and
and 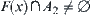 . Since
. Since  is connected and sets
is connected and sets  and
and  are separated, we have
are separated, we have 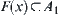 and
and  . This is in contradiction to
. This is in contradiction to 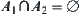 .
.
Therefore, 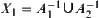 , i.e.,
, i.e., 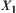 can be represented by the union of two mutually disjoint non-empty open sets. This is in contradiction to that
can be represented by the union of two mutually disjoint non-empty open sets. This is in contradiction to that 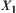 is connected.
is connected.
The theorem is proved.
Theorem 5.3
Proof
Let mapping 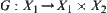 be
be 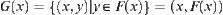 .
.
From the definition of the product topology, it is known that given  and a neighborhood
and a neighborhood  of
of 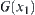 , for
, for  , there exists a neighborhood of z such that
, there exists a neighborhood of z such that 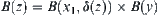 , where
, where 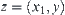 and
and 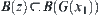 .
.
Since 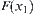 is compact
is compact 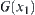 is also compact in
is also compact in 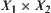 . Besides,
. Besides,  is an open covering of
is an open covering of 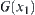 , then there exists a finite number of sub-coverings
, then there exists a finite number of sub-coverings 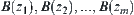 .
.
Let 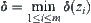 ,
, 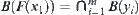 , where
, where 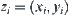 .
.
Therefore, we have 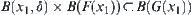 .
.
Finally, from the semi-continuity of F, for 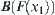 , there exists a neighborhood
, there exists a neighborhood  of
of 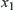 such that
such that 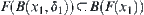 .
.
Letting 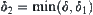 , for
, for 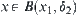 we have
we have
![]()
Thus, for 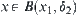 we have
we have
![]()
![]()
Namely, G is semi-continuous at 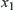 . Since
. Since 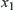 is an arbitrary point in
is an arbitrary point in 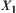 , G is semi- continuous on
, G is semi- continuous on 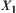 .
.
On the other hand, since  is connected, we have that
is connected, we have that 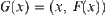 is also connected.
is also connected.
From Theorem 5.2, we conclude that 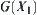 is a connected set in
is a connected set in 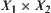 .
.
Theorem 5.4
For 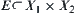 , E is compact.
, E is compact. 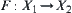 is a mapping corresponding to E, i.e.,
is a mapping corresponding to E, i.e., 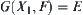 . Then, F is a semi-continuous mapping from
. Then, F is a semi-continuous mapping from 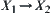 .
.
Proof
Since 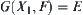 is compact, if F is not semi-continuous, there exist
is compact, if F is not semi-continuous, there exist 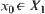 and
and 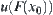 such that for any n, there has
such that for any n, there has 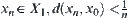 such that
such that  , where
, where  is a metric function on
is a metric function on 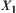 . Namely,
. Namely, 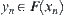 and
and 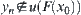 exist.
exist.
Let 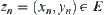 . Since
. Since 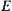 is compact, there exists a sub-sequence (still denoted by
is compact, there exists a sub-sequence (still denoted by 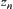 ) such that
) such that 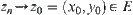 , i.e.,
, i.e., 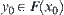 .
.
Since 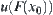 is open and
is open and 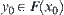 , there exists a positive number
, there exists a positive number 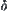 such that
such that  . Thus, there exists
. Thus, there exists 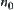 when
when 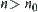 have
have  . This is in contradiction with
. This is in contradiction with 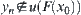 .
.
Therefore, F is semi-continuous.
Corollary 5.2
If moving object A is a polyhedron and the obstacles consist of a finite number of convex polyhedrons 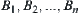 , then the rotation mapping
, then the rotation mapping  of A among the obstacles is a semi-continuous mapping, where D is the activity range of A, S is a unit sphere and C is a unit circle.
of A among the obstacles is a semi-continuous mapping, where D is the activity range of A, S is a unit sphere and C is a unit circle.
Proof
From Theorem 5.4, it’s only needed to prove that the RMG corresponding to A is compact.
Assume that 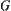 is a RMG corresponding to
is a RMG corresponding to 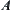 . Since
. Since 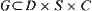 and sets
and sets 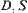 and
and 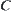 are bounded subsets in three-dimensional Euclidian space, from topology, it’s known that in n-dimensional Euclidian space, the necessary and sufficient condition of a compact set is that it’s a bounded closed set. Thus, in order to show the compactness of set
are bounded subsets in three-dimensional Euclidian space, from topology, it’s known that in n-dimensional Euclidian space, the necessary and sufficient condition of a compact set is that it’s a bounded closed set. Thus, in order to show the compactness of set 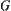 , it’s only needed to show that set
, it’s only needed to show that set 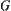 is closed.
is closed.
First we made the following agreement. When object 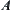 only touches obstacles, its state is still regarded as a point in
only touches obstacles, its state is still regarded as a point in 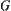 . When object
. When object 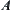 overlaps with obstacles, i.e., they have common inner points, its state is regarded as not belonging to
overlaps with obstacles, i.e., they have common inner points, its state is regarded as not belonging to 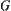 .
.
In order to show that 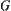 is closed, it’s only needed to show that the complement
is closed, it’s only needed to show that the complement 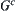 of
of 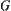 is open.
is open.
For any 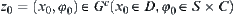 , from the above agreement, it’s known that when
, from the above agreement, it’s known that when 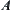 and obstacle
and obstacle 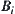 (may as well assume that
(may as well assume that 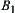 ) have common inner points, i.e., there exists
) have common inner points, i.e., there exists 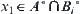 , where
, where 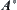 is an inner kernel of
is an inner kernel of 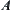 . Thus, there exists a neighborhood
. Thus, there exists a neighborhood 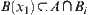 of
of 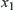 .
.
Assume that 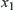 is a fixed point O. Some direction via point
is a fixed point O. Some direction via point 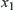 is denoted by
is denoted by 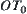 . Then
. Then 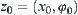 can be represented by
can be represented by 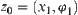 . In fact,
. In fact, 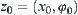 and
and 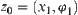 correspond the same position of A. The different representations of the same position in A due to the different options of its fixed point and direction.
correspond the same position of A. The different representations of the same position in A due to the different options of its fixed point and direction.
Let 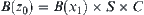 . Obviously,
. Obviously,  is a neighborhood of
is a neighborhood of 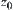 . Since
. Since  no matter A locates at arbitrary position of
no matter A locates at arbitrary position of  ,
, 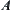 and
and 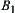 always have common inner points. In other words, any point in
always have common inner points. In other words, any point in  always belong to
always belong to 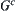 . Thus,
. Thus, 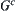 is open, i.e.,
is open, i.e., 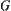 is closed.
is closed.
Theorem 5.5
Proof
From Theorem 5.3, we have that 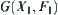 and
and 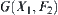 are connected. Since there exists a
are connected. Since there exists a 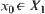 such that
such that 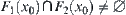 then
then 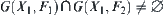 . From Property 5.3 in Section 5.3, we know that
. From Property 5.3 in Section 5.3, we know that 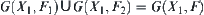 is a connected set.
is a connected set.
Theorems 5.2–5.5 underlie the basic principle of the dimension reduction method that related to the connectivity structure of a set in a product space. Namely, the connectivity problem of a set 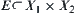 , or an image
, or an image 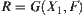 in the product space
in the product space 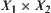 , under certain conditions can be transformed to that of considering the connectivity of domain
, under certain conditions can be transformed to that of considering the connectivity of domain 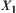 and
and  , respectively. Since
, respectively. Since  obviously the dimensions of both
obviously the dimensions of both 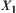 and
and  are lower than that of
are lower than that of 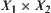 . So the dimension is reduced.
. So the dimension is reduced.
Furthermore, if 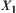 or
or  is also a product space, then a set on
is also a product space, then a set on 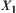 or
or  can be regarded as an image of a mapping in an even lower space. By repeatedly using the same principle, a high-dimensional problem can be decomposed into a set of one-or two-dimensional problems.
can be regarded as an image of a mapping in an even lower space. By repeatedly using the same principle, a high-dimensional problem can be decomposed into a set of one-or two-dimensional problems.
In the collision-free paths planning, its state space can be regarded as an image of mapping  . From Theorem 5.2, the state space can also be regarded as an image of mapping
. From Theorem 5.2, the state space can also be regarded as an image of mapping 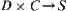 ,
, 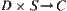 or
or 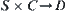 . Therefore, according to the concrete issue, we can choose state space representations based on different mappings which will bring considerable convenience to path planning.
. Therefore, according to the concrete issue, we can choose state space representations based on different mappings which will bring considerable convenience to path planning.
In fact, the dimension reduction method is one of the specific applications of the truth and falsity preserving principles in quotient space theory.
5.4.2. Characteristic Network
In Section 5.3, we presented a general principle for constructing a characteristic network which represents the connected structure of a set. In this section, we will use the dimension reduction method for constructing the characteristic network.
The Connected Decomposition of a Mapping
In Section 5.3, the concept of the homotopically equivalent class is introduced. We now extend the concept to sets in general product spaces.
Definition 5.15
(1) 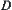 and
and 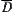 are arcwise connected on X
are arcwise connected on X
(2) Assume that 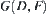 , the image of F on D, has m connected components
, the image of F on D, has m connected components 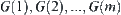 , then
, then 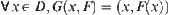 has just m connected components.
has just m connected components.
(3) If 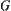 has m components
has m components 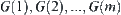 then
then 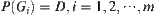 , where
, where 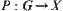 is a projection. Then,
is a projection. Then, 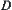 is said to be a homotopically equivalent class of
is said to be a homotopically equivalent class of 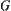 with respect to X, or
with respect to X, or 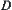 is a homotopically equivalent class for short.
is a homotopically equivalent class for short.
If 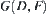 has m connected components, denoted by
has m connected components, denoted by 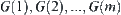 , letting
, letting 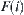 be a mapping corresponding to
be a mapping corresponding to 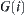 , then
, then 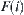 is called the connected decomposition of F with respect to D.
is called the connected decomposition of F with respect to D.
Let's see an example.
Example 5.6
Now, 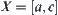 is decomposed into two homotopically equivalent classes
is decomposed into two homotopically equivalent classes 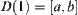 and
and 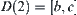 .
.
Graph  has two connected components
has two connected components 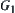 and
and 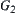 . Their corresponding mappings are
. Their corresponding mappings are 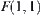 and
and 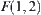 , respectively.
, respectively.
Graph 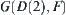 has one component
has one component  . Its corresponding mapping is
. Its corresponding mapping is 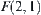 .
.
Thus,  is the connected decomposition of
is the connected decomposition of 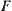 .
.  is called a connected component of
is called a connected component of 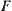 on
on 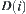 .
.
The Construction of Characteristic Networks
The connected decompositions of 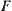 on
on 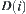 are
are 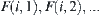 . Let
. Let
![]()
The construction of a characteristic network is as follows.
(1) For each 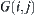 , constructing a node
, constructing a node 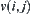 , we have a set
, we have a set 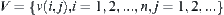 of nodes.
of nodes.

(2) For  and
and 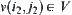 , if their corresponding components
, if their corresponding components 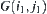 and
and 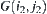 are neighboring in
are neighboring in 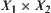 , i.e., the intersection of their closures is non-empty, then
, i.e., the intersection of their closures is non-empty, then  and
and 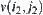 is said to be neighboring.
is said to be neighboring.
(3) Linking each pair of neighboring nodes in 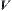 with an edge, we have a network
with an edge, we have a network 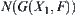 . It is called a characteristic network corresponding to
. It is called a characteristic network corresponding to 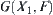 , or a characteristic network corresponding to F.
, or a characteristic network corresponding to F.
Proposition 5.6
Note that a 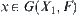 corresponds to a node
corresponds to a node 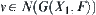 that means
that means 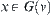 , where
, where 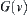 is a set of
is a set of 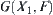 corresponding to node
corresponding to node  .
.
Example 5.7
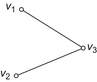
A set 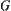 as shown in Fig. 5.17 is given.
as shown in Fig. 5.17 is given. 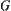 is decomposed into sets
is decomposed into sets  and
and  as shown in Fig. 5.17. Its characteristic network is shown in Fig. 5.18.
as shown in Fig. 5.17. Its characteristic network is shown in Fig. 5.18.
Note that to judge the neighboring relationship between 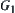 and
and 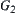 , their closures
, their closures 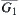 and
and 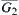 are constructed only on
are constructed only on  . Since the intersection between their closures is empty,
. Since the intersection between their closures is empty, 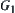 and
and 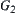 are not neighboring. However, to judge the neighboring relationship between
are not neighboring. However, to judge the neighboring relationship between 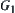 and
and  , their closures are constructed on
, their closures are constructed on 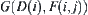 .
.
Generally, to judge the neighboring relationship between two sets 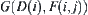 and
and 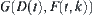 , their closures are constructed on
, their closures are constructed on 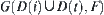 .
.
Certainly,  can also be decomposed into three homotopically equivalent classes
can also be decomposed into three homotopically equivalent classes  and
and 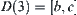 . And we have a characteristic network as shown in Fig. 5.19.
. And we have a characteristic network as shown in Fig. 5.19.
Where
![]()
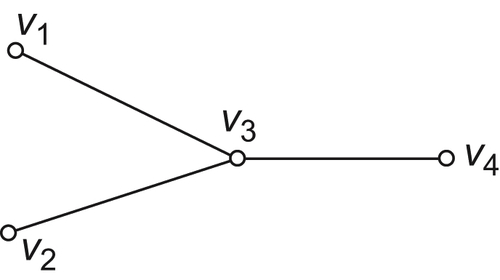
Obviously, if  is decomposed into the union of maximal sets of homotopically equivalent classes, the number of nodes in the corresponding characteristic network will be minimal.
is decomposed into the union of maximal sets of homotopically equivalent classes, the number of nodes in the corresponding characteristic network will be minimal.
Finally, we analyze the dimension reduction method from quotient space based granular computing view point.
Now 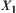 is decomposed into the union
is decomposed into the union 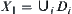 of homotopically equivalent classes. For
of homotopically equivalent classes. For 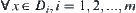 ,
,  , is regarded as a quotient space composed by equivalence classes and is denoted by
, is regarded as a quotient space composed by equivalence classes and is denoted by  . Each element on
. Each element on  is a connected set on
is a connected set on 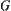 . The problem solving in space
. The problem solving in space 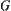 can be transformed into the corresponding problem solving on
can be transformed into the corresponding problem solving on  since these two spaces have the truth preserving property.
since these two spaces have the truth preserving property.
If regarding 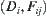 as an equivalence class, we have a quotient space
as an equivalence class, we have a quotient space  . It still has the truth preserving property; so the original problem can also be transformed into a corresponding problem in
. It still has the truth preserving property; so the original problem can also be transformed into a corresponding problem in  space. Moreover, the problem in
space. Moreover, the problem in  can be further transformed into a corresponding problem in a characteristic network. Thus, the characteristic network method of path planning is an application of quotient space theory.
can be further transformed into a corresponding problem in a characteristic network. Thus, the characteristic network method of path planning is an application of quotient space theory.
Collision-Free Paths Planning
Assume that a moving object A is a polyhedron with a finite number of vertices and the obstacles 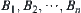 are convex polyhedrons with a finite number of vertices.
are convex polyhedrons with a finite number of vertices.
Let 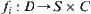 be the rotation mapping of A with respect to obstacle
be the rotation mapping of A with respect to obstacle 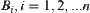 , i.e.,
, i.e., 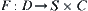 is an intersection mapping of
is an intersection mapping of 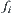 .
.
Let  be the connected decompositions of
be the connected decompositions of 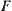 .
.
According to the preceding procedure, we may have a characteristic network 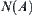 and the following proposition.
and the following proposition.
Proposition 5.7
Given an initial state 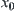 and a goal state
and a goal state 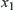 , if
, if 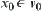 and
and 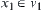 then object A can move from
then object A can move from 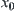 to
to 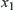 without collision, if and only if there exists a connected path from
without collision, if and only if there exists a connected path from 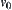 to
to 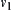 on
on 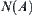 .
.
An Example
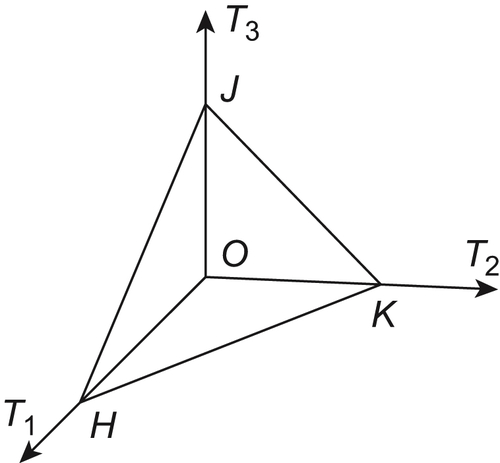
Assume that the moving object A is a tetrahedron (Fig. 5.20). The initial coordinates of its four vertices are 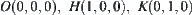 and
and 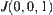 . Plane
. Plane 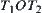 is an obstacle.
is an obstacle.
We next analyze the topologic structure of the RMG of the tetrahedron A due to obstacle 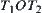 .
.
The state of a rigid object A can be defined by the coordinates of any non-colinear three points on A, e.g.,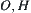 and
and  . The coordinate of the point O is
. The coordinate of the point O is 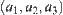 . Its range is the upper half space, i.e.,
. Its range is the upper half space, i.e., 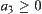 and is denoted by D. If point O is fixed, the range of H is a unit sphere S with O as its center and
and is denoted by D. If point O is fixed, the range of H is a unit sphere S with O as its center and 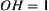 as its radius, i.e.,
as its radius, i.e., 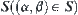 . If points O and H are fixed, the range of K is a unit circle C with O as its center. And the circle is on the plane perpendicular to line OH via K, i.e.,
. If points O and H are fixed, the range of K is a unit circle C with O as its center. And the circle is on the plane perpendicular to line OH via K, i.e.,  . Generally, D, S and C are represented by rectangular, sphere and polar coordinate systems, respectively.
. Generally, D, S and C are represented by rectangular, sphere and polar coordinate systems, respectively.
The RMG of the moving object A is a subset of space 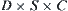 (six-dimensional), i.e., the state space of A.
(six-dimensional), i.e., the state space of A.
From Section 5.3, we know that the RMG of A can be regarded as an image of mapping 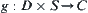 . Since the obstacle is a plane, the state space of A remains unchanged for coordinates
. Since the obstacle is a plane, the state space of A remains unchanged for coordinates 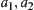 and horizontal angle
and horizontal angle 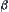 on S; so it’s only related to three parameters, i.e.,
on S; so it’s only related to three parameters, i.e., 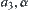 and
and  .
.
Now, we discuss its characteristic network.
(1) Fix 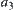 and
and  , to find
, to find 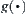 .
.
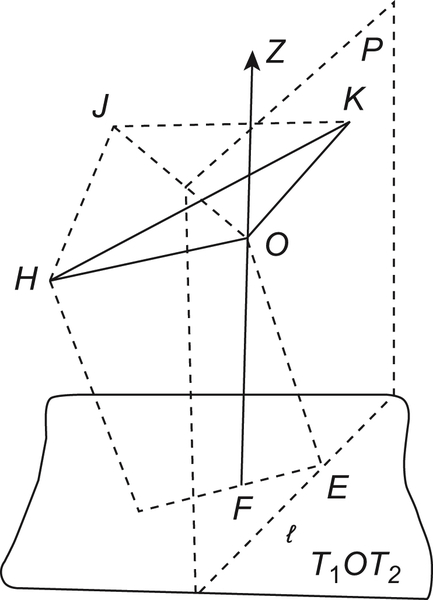
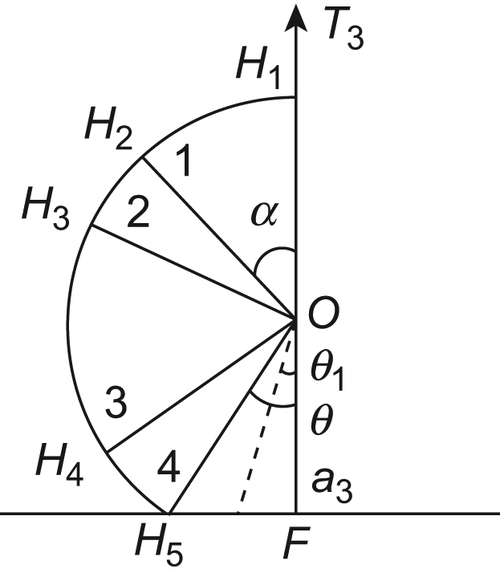
As shown in Fig. 5.21, through K we compose a plane P perpendicular to line OH. l is an intersecting line between planes P and 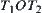 . Through line OH we compose a plane perpendicular to
. Through line OH we compose a plane perpendicular to 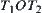 . OE is an intersecting line between the composed plane and P.
. OE is an intersecting line between the composed plane and P.
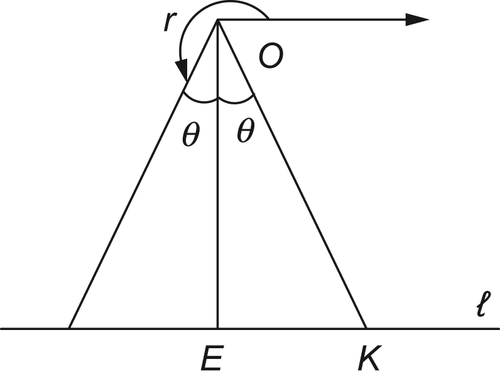
As shown in Fig. 5.22, in plane P, the line through point O and parallel to l is used as a reference axis. The position of point K can be represented by the angle  related to the axis.
related to the axis.
Obviously, if 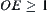 , the range of point K is the entire unit circle and is denoted by
, the range of point K is the entire unit circle and is denoted by 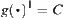 .
.
Similarly, the range of point J is also the same circle when it is transformed to a constraint of point K, i.e., 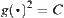 .
.
Thus, 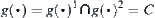 , i.e.,
, i.e., 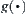 has only one component.
has only one component.
When 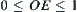 ,
, 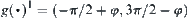 and
and 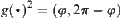 , where
, where  .
.
The second component will disappear when 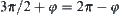 , i.e.,
, i.e., 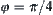 . Therefore, when
. Therefore, when  , the mapping has two components. When
, the mapping has two components. When 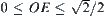 , it has only one component.
, it has only one component.
(2) The relationship between 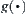 and OH
and OH
In (1) we discuss the relation between 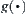 and OE. Actually, the length of OE depends on the position of OH, i.e., coordinate
and OE. Actually, the length of OE depends on the position of OH, i.e., coordinate 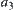 and
and  .
.
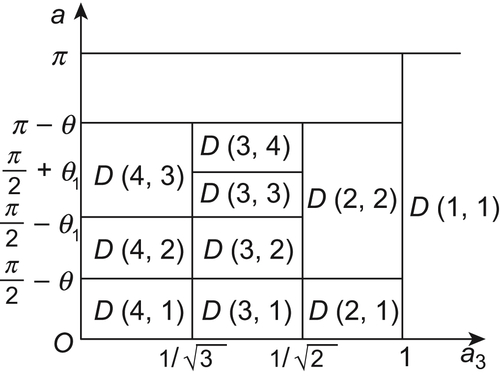
Assume that the coordinate of the point O is 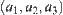 . The coordinate
. The coordinate 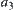 is divided into four intervals: (i)
is divided into four intervals: (i)  , (ii)
, (ii) 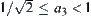 , (iii)
, (iii) 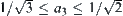 , (iv)
, (iv) 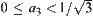 . Each interval of
. Each interval of 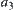 is further divided into several sub-intervals based on the value of
is further divided into several sub-intervals based on the value of  .
.
The partition of 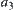 and
and  is shown below (Fig. 5.23), where
is shown below (Fig. 5.23), where  ={the i-th interval of
={the i-th interval of 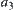 , the j-th interval of
, the j-th interval of  }.
}.
To show the procedure of calculating 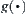 , we take interval
, we take interval 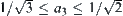 as an example.
as an example.
Fixing point O, through O we compose a line  parallel to
parallel to 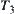 -axis (Fig. 5.24). The position of OH is defined by angle
-axis (Fig. 5.24). The position of OH is defined by angle  . Then, angle
. Then, angle  is divided into four intervals.
is divided into four intervals.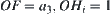 . When
. When 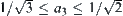 , the range of point H on S is
, the range of point H on S is 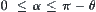 , where
, where 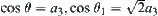 and
and 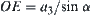 .
.
![]()
We can write that
When  ,
, 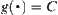 since
since 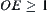 .
.
When 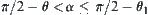
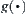 has two components since
has two components since 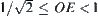 .
.
When 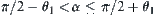 ,
, 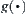 has one component since
has one component since 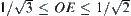 .
.
When 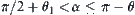 ,
, 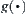 has two components since
has two components since 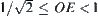 .
.
Let 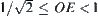 be the k-th component of
be the k-th component of 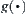 on
on  . If
. If  is connected, then it is denoted by
is connected, then it is denoted by 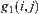 .
.
Let  , i.e.,
, i.e.,  is the image of
is the image of 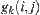 .
.
Similarly, we have the following results.
When  ,
,  has one component, i.e.,
has one component, i.e., 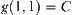 ,
,  .
.
When 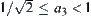 ,
,
When 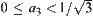
(3) Characteristic network
Each  corresponds to a node
corresponds to a node 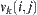 . We have a set V of nodes.
. We have a set V of nodes.
Nodes 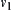 and
and  of V are neighboring if their corresponding
of V are neighboring if their corresponding 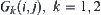 , are neighboring in the state space.
, are neighboring in the state space.
Linking any pair of neighboring nodes by an edge, we obtain a characteristic network 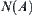 (Fig. 5.25).
(Fig. 5.25).
(4) Find collision-free paths
And given a goal state 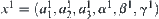 , where
, where
![]()
![]()
![]()
![]()
Then,
![]()
From the characteristic network 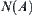 , we have a collision-free path of A.
, we have a collision-free path of A.
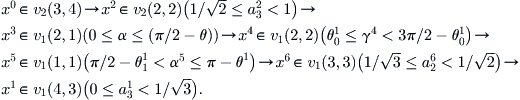
Note that only one parameter changes in each step. For example, from state  , only the coordinate
, only the coordinate 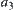 changes from
changes from 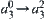 . The range of each parameter is indicated in the brackets.
. The range of each parameter is indicated in the brackets.
The moving process of A is shown in Fig. 5.26.
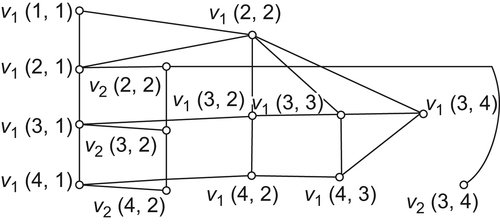
(5) Conclusions
The configuration space representation and the like are usually used in both geometric and topologic approaches to motion planning. The main difference is that in the geometric model the geometric structure of 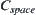 is investigated, while in the topologic model only the topologic structure is concerned.
is investigated, while in the topologic model only the topologic structure is concerned.
Taking the ‘piano-mover’ problem as an example, by the subdivision algorithm presented in Brooks and Lozano-Perez (1982), the real 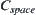 is divided. Even though the connectivity network constructed consists of 2138 arcs linking 1063 nodes, it is still an approximation of the real
is divided. Even though the connectivity network constructed consists of 2138 arcs linking 1063 nodes, it is still an approximation of the real 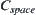 . But in the topologic algorithm (see Section 5.5 for the details), the characteristic network constructed only consists of 23 nodes linked by 32 arcs, however, it is homotopically equivalent to the real
. But in the topologic algorithm (see Section 5.5 for the details), the characteristic network constructed only consists of 23 nodes linked by 32 arcs, however, it is homotopically equivalent to the real 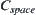 . Therefore, from the connectivity point of view, the topologic model is precise (Zhang et al., 1990a).
. Therefore, from the connectivity point of view, the topologic model is precise (Zhang et al., 1990a).

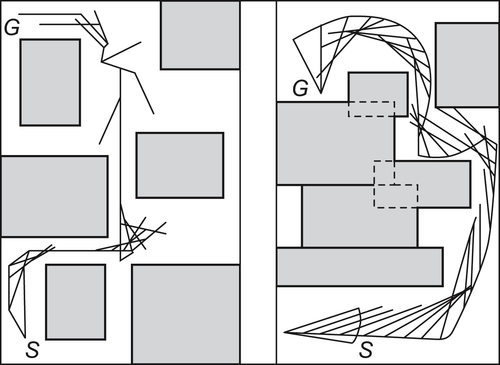
Since in topologic model, the motion proceeds in the coarse-grained world the computational complexity may be reduced under certain conditions. In 1980s we implemented the ‘piano-mover’ problem by topologic method on PDP 11/23 machine. The program is written by FORTRAN 4 and takes about dozens of seconds CPU time for implementation. More results will be given in Section 5.5. We also implemented dozens of experiments on ALR-386/II machine for a 2D rod moving among obstacles using programing language PASCAL and take less than 15 seconds time for implementation. One of the examples is shown in Fig. 5.27.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
