4.7. Fuzzy Reasoning Based on Quotient Space Structures
In this section, we present a framework of fuzzy reasoning based on quotient space structures. They are: (1) introduce quotient structure into fuzzy set theory, i.e., establish fuzzy set representations and their relations in multi-granular spaces, (2) introduce the concept of fuzzy set into quotient space theory, i.e., fuzzy equivalence relation and its reasoning, (3) the transformation of three different granular computing methods, (4) the methods for transforming statistical reasoning models into quotient space structures. The combination of the two (fuzzy set and quotient space) methodologies is intended to embody the language-processing capacity of fuzzy set method and multi-granular computing capacity of quotient space method (Zhang and Zhang, 2003a, 2003b, 2003d).
There are three basic methods for granular computing, fuzzy set (Zadeh, 1979, 1997, 1999), rough set (Pawlak, 1982, 1991, 1998) and quotient space theory (Zhang and Zhang, 2003c). In fuzzy set theory, concepts are represented by natural language. So the theory is a well-known language-formalized model and one of granular computing favorable tools. We believe that a concept can be represented by a subset. Different concepts reflect different grain-size subsets. A family of concepts composes a partition of whole space. Thus, different families of concepts constitute different quotient spaces (knowledge bases). The aim of granular computing is to investigate the relation and translation among subsets under a given knowledge base. The same problem can be studied in different quotient spaces (knowledge bases). Then the results from different quotient spaces are synthesized together to further understand the problem. We intend to combine the two methods and apply to fuzzy reasoning.
4.7.1. Fuzzy Set Based on Quotient Space Model
Definition 4.4
is a fuzzy set on quotient space 
. Define its membership function as 
, where 
. f is a given function.When the membership function of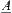 
is regarded as attribute function f on X, the fuzzy processing on quotient spaces is equivalent to the projection, synthesis and decomposition of attribute function f under the quotient space framework. Let us see an example.
is regarded as attribute function f on X, the fuzzy processing on quotient spaces is equivalent to the projection, synthesis and decomposition of attribute function f under the quotient space framework. Let us see an example.A reasoning rule: ‘if u is a, then u is b’. When a and b are fuzzy concepts, the rule becomes a fuzzy reasoning rule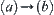 
.
.Assume that a and b are described by fuzzy sets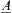 
on X and 
on Y, respectively. Then rule 
can be represented by a fuzzy relation from X to Y, or a fuzzy subset on 
denoted by 
. We have
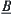on X and on Y, respectively. Then rule 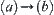can be represented by a fuzzy relation from X to Y, or a fuzzy subset on 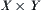denoted by 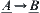. We have
Using the above rule, if input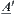 
then we have 
as follows
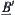then we have as follows
(4.21)
Assume that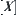 
is a quotient space of X. If regarding 
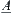and 
as f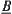uzzy sets on 
, two questions have to be answered, i.e., what is the result obtained when regarding Formula (4.21) as a reasoning rule? What is the relation between the above result and the reasoning result obtained from space X?
is a quotient space of X. If regarding and as fuzzy sets on 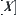, two questions have to be answered, i.e., what is the result obtained when regarding Formula (4.21) as a reasoning rule? What is the relation between the above result and the reasoning result obtained from space X?
is a fuzzy set on X. 
is an induced fuzzy set on 
and defined as follows.
(4.22)
(4.23)
The quotient membership functions defined by Formulas (4.22) and (4.23) are quotient fuzzy subsets defined by the maximal and minimal principles.
For notational simplicity, in the following discussion, the underline below the signs of fuzzy sets is omitted.
Theorem 4.2 (Weakly Falsity- or Truth-Preserving Principle)
and B are fuzzy subsets on 
and 
, respectively. 
is a quotient space of X. 
and 
are fuzzy subsets on 
and 
induced from 
and B, according to the maximal and minimal principles. 
is inferred from 
based on rule 
. 
is inferred from 
based on rule 
. We have
(4.24)
(4.25)
Formulas (4.24) and (4.25) show the falsity- and truth-preserving principles of fuzzy reasoning on quotient spaces in some sense. For example, if a fuzzy concept having degree of membership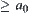 
is regarded as ‘truth’, otherwise as ‘falsity’, Formula (4.24) embodies the falsity-preserving principle of fuzzy reasoning. If 
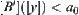, then 
. Namely, if the degree of membership of a conclusion (y) on a quotient space is 
then degree of membership of the corresponding conclusion (y) on the original space must be 
. Similarly, Formula (4.25) embodies the truth-preserving principle of fuzzy reasoning, where 
, then 
.
is regarded as ‘truth’, otherwise as ‘falsity’, Formula (4.24) embodies the falsity-preserving principle of fuzzy reasoning. If , then . Namely, if the degree of membership of a conclusion (y) on a quotient space is 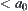then degree of membership of the corresponding conclusion (y) on the original space must be 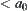. Similarly, Formula (4.25) embodies the truth-preserving principle of fuzzy reasoning, where 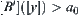, then 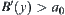.The definition of membership functions on quotient spaces can be defined in different ways. Then, the relation of fuzzy reasoning between quotient spaces is different. However, the fuzzy reasoning can always benefit by the truth- and falsity-preserving principle and the like.
4.7.2. Fuzzified Quotient Space Theory
Fuzzy concepts can be introduced to quotient space theory in different ways, for example, introduce fuzzy concepts to domain X, fuzzy structures to topologic structure T, etc. In the section, fuzzy equivalence relations are introduced to fuzzy reasoning.
From Section 2.4, the following theorem holds.
Basic Theorem
The following three statements are equivalent:
(1) A fuzzy equivalence relation on X
(2) A normalized isosceles distance on some quotient space of X
(3) A hierarchical structure on X.
From the theorem, it’s known that a fuzzy equivalence relation is equivalent to a deterministic distance so that a fuzzy problem can be handled under the deterministic framework. Second, in quotient space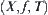 
, T is an inherent topologic structure of X and independent of distance d introduced from fuzzy equivalence relation. Third, quotient space 
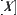is composed by 
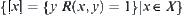. If we define a quotient space as 
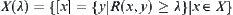, then define a distance function on 
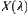as 
, where 
and
, T is an inherent topologic structure of X and independent of distance d introduced from fuzzy equivalence relation. Third, quotient space is composed by . If we define a quotient space as , then define a distance function on as 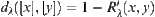, where 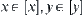and
(4.26)
It can be proved that the definition by Formula (4.26) is unique for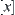 
and 
. 
is a distance function on 
. 
is a sequence of nested quotient spaces (metric spaces). If 
, then 
is a quotient space of 
. Space 
consists of one point.
and 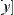. 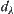is a distance function on 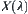. 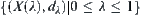is a sequence of nested quotient spaces (metric spaces). If 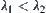, then 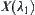is a quotient space of 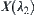. Space 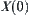consists of one point.
is a topologic space. Now a quotient topology 
is introduced to each quotient space 
of 
. Then, 
has two structures 
, i.e., a multi-structure space, one induced from topology, one induced from fuzzy concept. Actually, for example, the interpersonal relationship is a multi-structure space, where the relationship of their place of residence amounts to T and their blood relationship amounts to 
.Fixed x, regarding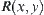 
as a membership function of a fuzzy subset, we have a space 
composed by fuzzy subsets on 
. If the reasoning on 
is the same mode as in common quotient spaces, then 
represents the precision of its conclusions, i.e., the nearer the distance 
the more accurate the conclusions.
as a membership function of a fuzzy subset, we have a space 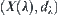composed by fuzzy subsets on 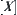. If the reasoning on 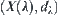is the same mode as in common quotient spaces, then 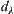represents the precision of its conclusions, i.e., the nearer the distance 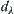the more accurate the conclusions.4.7.3. The Transformation of Three Different Granular Computing Methods
Fuzzy set, rough set and quotient space-based granular computing have different perspectives and goals. But they have a close relationship.
In rough set, a problem is represented by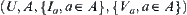 
, where U is a domain, A is a set of attributes, 
is an attribute function, and 
is the range of a. When 
is discrete, domain U is generally partitioned by 
. By combining different 
then we have different partitions of U. When 
is continuous, 
is discretized. Then, U is partitioned as the same as the discrete case.
, where U is a domain, A is a set of attributes, 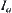is an attribute function, and 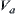is the range of a. When 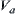is discrete, domain U is generally partitioned by 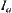. By combining different 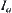then we have different partitions of U. When 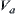is continuous, 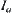is discretized. Then, U is partitioned as the same as the discrete case.In other words, normalizing the attribute function, i.e.,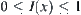 
, it can be regarded as a fuzzy set on U. If given a data table, it can be transformed to a set of fuzzy sets on U. Then, mining a data table is equivalent to studying a set of fuzzy sets.
, it can be regarded as a fuzzy set on U. If given a data table, it can be transformed to a set of fuzzy sets on U. Then, mining a data table is equivalent to studying a set of fuzzy sets.On the other hand, given a set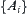 
of fuzzy sets on X, for each fuzzy set 
, letting 
be a family of open sets, then from 
we have a family of open sets. Using the open sets, a topologic structure T on U can be uniquely defined. We have a topologic space 
. Then, the study of a family 
of fuzzy sets can be transformed to that of topologic space 
. The study of space 
may use the quotient space method. Thus, the quotient space method is introduced to the study of fuzzy sets. The concept of granularity represented by fuzzy set is transformed to a deterministic topologic structure. So the quotient space method provides a new way of granular computing.
of fuzzy sets on X, for each fuzzy set 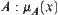, letting 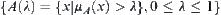be a family of open sets, then from 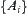we have a family of open sets. Using the open sets, a topologic structure T on U can be uniquely defined. We have a topologic space 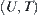. Then, the study of a family 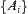of fuzzy sets can be transformed to that of topologic space 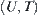. The study of space 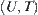may use the quotient space method. Thus, the quotient space method is introduced to the study of fuzzy sets. The concept of granularity represented by fuzzy set is transformed to a deterministic topologic structure. So the quotient space method provides a new way of granular computing.Conversely, given a topologic space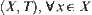 
, letting 
={all open sets containing x}, 
is called a neighborhood system of x. According to (Yao and Zhong, 1999), neighborhood system 
can be regarded as a qualitative fuzzy set. So a topology space 
can be regarded as a family of fuzzy sets. A neighborhood system description of a fuzzy set is presented in Lin (1996, 1997) and Yao and Chen (1997).
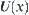, letting ={all open sets containing x}, 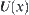is called a neighborhood system of x. According to (Yao and Zhong, 1999), neighborhood system 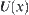can be regarded as a qualitative fuzzy set. So a topology space 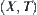can be regarded as a family of fuzzy sets. A neighborhood system description of a fuzzy set is presented in Lin (1996, 1997) and Yao and Chen (1997).The three granular computing methods can be converted to each other. The integration of these methods is a subject worthy of further study.
4.7.4. The Transformation of Probabilistic Reasoning Models
In the section, we will discuss how to transform a probabilistic description to a deterministic model.
We have given reasoning model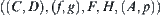 
based on quotient space theory (Sections 4.1–4.4). A function 
defined on edge 
is regarded as a probability, i.e., the conditional probability of b given a. Let 
, i.e., 
is regarded as a distance from a to b (a topologic structure 
). The finding of a solution from A to goal p with maximal probability is equivalent to that of the shortest path from A to p under distance d. Assume that if 
is the solution with maximal probability, then its probability is 
, from 
, we have 
. So the maximal probability solution (the former) is equivalent to the shortest path finding (the latter).
based on quotient space theory (Sections 4.1–4.4). A function 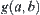defined on edge 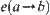is regarded as a probability, i.e., the conditional probability of b given a. Let 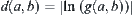, i.e., 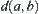is regarded as a distance from a to b (a topologic structure 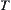). The finding of a solution from A to goal p with maximal probability is equivalent to that of the shortest path from A to p under distance d. Assume that if 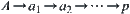is the solution with maximal probability, then its probability is 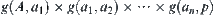, from 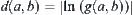, we have 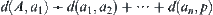. So the maximal probability solution (the former) is equivalent to the shortest path finding (the latter).Reasoning on a probabilistic model can be transformed to a deterministic shortest path-finding problem, i.e., non-deterministic concepts such as fuzzy and probability are transformed to deterministic structures. Therefore, deterministic and non-deterministic problems can be studied under the same framework. Especially, in multi-granular computing, under quotient space structures, the falsity- and truth-preserving principles, projection, and synthetic methods that we have discussed in the previous sections can be used in either deterministic or non-deterministic case.
4.7.5. Conclusions
In the section, the falsity- and truth-preserving principles of reasoning are proposed. The principles show that introducing structure into the quotient space model is very important, that is, domain structure is an important concept in granular computing. We also show that the combination of quotient space method and other methods will provide a new way for granular computing.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.