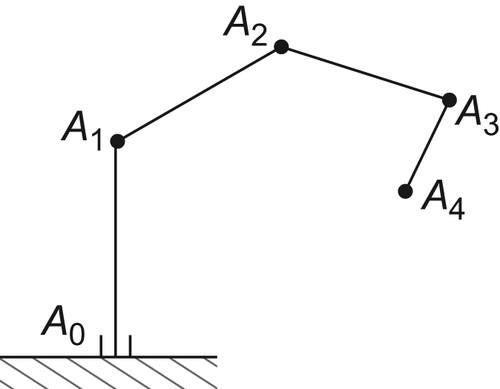
5.5. Applications
In this section, the theory and technique presented in the preceding sections will be applied to two motion planning problems. One is the planning for a planar rod moving among obstacles. The other is the planning for a multi-joint arm (Zhang and Zhang, 1982a, 1982b, 1988b, 1990a).
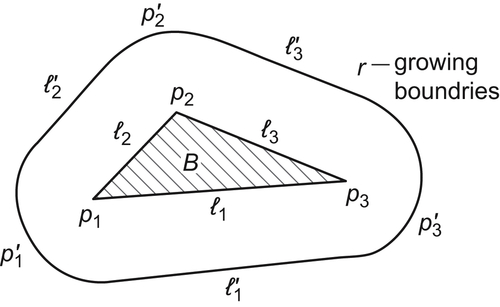
The main point for using the theory to a real motion planning problem is how to decompose the domain into homotopically equivalent classes. There are three kinds of boundaries which are used for the decomposition. Namely, the original boundaries of the obstacles, the r-growing boundaries of the obstacles, and some specific curves called the disappearance curves arising in the regions cluttered up with the obstacles.
5.5.1. The Collision-Free Paths Planning for a Planar Rod
Assume that the length of rod A is r. The obstacles are assumed to be composed of a finite number of convex polygons. One of the end points of rod A is regarded as a fixed point O. The activity range of point O is a region in a two-dimensional plane. The rod itself is regarded as a reference axis OT. The activity range of OT-axis is its orientation angle.
The state space of A is X. We regard X as an image of mapping 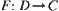 , where D is the activity range of point O and C is a unit circle.
, where D is the activity range of point O and C is a unit circle.
The Homotopically Equivalent Decomposition of Domain D
Definition 5.16
Assume that the length of rod A is r. We define the r-growing boundaries of obstacles as follows.
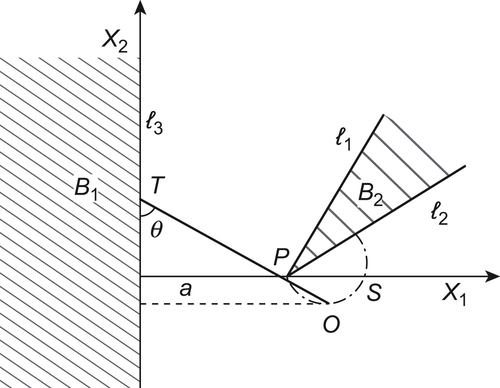
As shown in Fig. 5.28, B is an obstacle. We construct new lines parallel to and at a distance r from each edge of B, and draw arcs with each vertex of B as its center and r as its radius which are tangent to the new lines. The boundary composed of these new lines and arcs is called the r-growing boundary of obstacle B (Fig. 5.28).
Definition 5.17
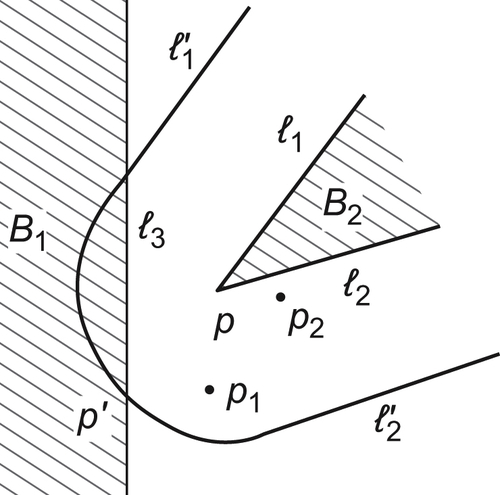
As shown in Fig. 5.29, at point 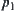 there exist the feasible orientations of OT along the direction of the lane, but at point
there exist the feasible orientations of OT along the direction of the lane, but at point 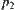 there does not have any feasible orientation since it is blocked by obstacle
there does not have any feasible orientation since it is blocked by obstacle 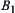 . Under the edge
. Under the edge 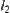 , there is an area where rod A does not have any feasible orientation along the direction of the lane. It is called a shaded area. The boundary of the shaded area can be computed as follows.
, there is an area where rod A does not have any feasible orientation along the direction of the lane. It is called a shaded area. The boundary of the shaded area can be computed as follows.
As shown in Fig. 5.30, we regard the boundary 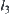 as
as 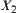 -axis, the line perpendicular to
-axis, the line perpendicular to 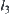 through point p as
through point p as 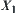 -axis and the angle
-axis and the angle  formed by OT and
formed by OT and 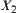 -axis as a parameter. The equations of the boundary S of the shaded area are shown below.
-axis as a parameter. The equations of the boundary S of the shaded area are shown below.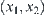 is the coordinate of the points on S,
is the coordinate of the points on S, 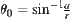 ,
,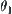 is the angle formed by
is the angle formed by  and
and  -axis, and a is the distance between point p and boundary
-axis, and a is the distance between point p and boundary  .
.
![]()
![]()
The boundary S is called a disappearance curve, since some orientation components will disappear when the rod going across the boundary.
The Decomposition of the Homotopically Equivalent Classes
The original boundaries and r-growing boundaries of obstacles and the disappearance curves will divide domain D into several connected regions denoted by 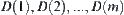 .
.
We will show that 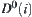 is a homotopically equivalent class, where set
is a homotopically equivalent class, where set 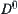 is the inner kernel of D.
is the inner kernel of D.
Let 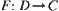 be the rotation mapping of A. Given
be the rotation mapping of A. Given 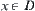 , it is easy to find
, it is easy to find 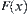 or each component of
or each component of 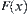 .
.
Given 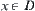 , using x as center and r as radius, we draw a circle C counter clockwise. C is divided into several arcs by the central projections of obstacles from x on C. Then each arc corresponds to a component of
, using x as center and r as radius, we draw a circle C counter clockwise. C is divided into several arcs by the central projections of obstacles from x on C. Then each arc corresponds to a component of 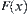 .
.
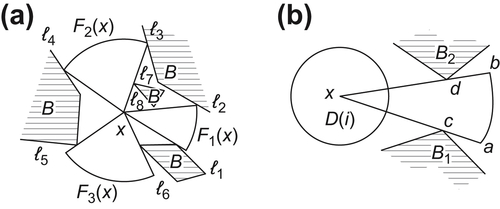
As shown in Fig. 5.31(a), 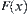 is decomposed into three components
is decomposed into three components 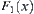 ,
,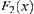 and
and 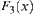 . As shown in Fig. 5.31(b), each arc
. As shown in Fig. 5.31(b), each arc 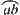 corresponds to a component
corresponds to a component 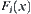 . c(d) is the point of intersection between obstacle B1 (B2) and radius ax(bx). Points c and d are called intersection points of component
. c(d) is the point of intersection between obstacle B1 (B2) and radius ax(bx). Points c and d are called intersection points of component 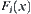 on obstacles or simply the intersection points of
on obstacles or simply the intersection points of 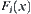 . As shown in Fig. 5.31(a), component
. As shown in Fig. 5.31(a), component 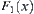 can be represented by (1,2) or (8,2), where numbers 1, 2 and 8 indicate the numbers of edges l1, l2 and l8 of obstacles, respectively. And the intersection points of
can be represented by (1,2) or (8,2), where numbers 1, 2 and 8 indicate the numbers of edges l1, l2 and l8 of obstacles, respectively. And the intersection points of 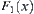 locate in edges l1, l2 and l8. Similarly,
locate in edges l1, l2 and l8. Similarly, 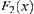 is denoted by (3,4), (7,4) or (9,4), etc. By this notation a component may have different representations but they should be regarded as being the same component.
is denoted by (3,4), (7,4) or (9,4), etc. By this notation a component may have different representations but they should be regarded as being the same component.
Definition 5.18
Then F is said to be continuous at 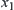 . If
. If 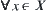 , F is continuous, then F is said to be continuous on X.
, F is continuous, then F is said to be continuous on X.
Proposition 5.8
The 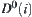 defined above is a homotopically equivalent class with respect to the rotation mapping F of rod OT, i.e., F is continuous on
defined above is a homotopically equivalent class with respect to the rotation mapping F of rod OT, i.e., F is continuous on 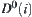 .
.
Proof
If arc 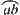 is degraded into a point, then x is a point at the boundary of some shaded area or a is a concave vertex of some obstacle. This is a contradiction.
is degraded into a point, then x is a point at the boundary of some shaded area or a is a concave vertex of some obstacle. This is a contradiction.
If 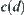 is a vertex of some obstacle, then
is a vertex of some obstacle, then 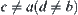 . Otherwise, x belongs to a vertex of some r-growing boundary. This is a contradiction, too.
. Otherwise, x belongs to a vertex of some r-growing boundary. This is a contradiction, too.
Thus, the length of 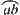 is assumed to be positive, a and b are not vertices of obstacles and sector
is assumed to be positive, a and b are not vertices of obstacles and sector 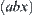 is at a positive distance from the rest of obstacles except
is at a positive distance from the rest of obstacles except  and
and  . Therefore, given
. Therefore, given 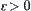 ,
,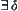 for
for 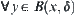 , we construct every rounds with y as its center and r (the length of the rod) as its radius. The sectors, parts of the rounds that locate between obstacles
, we construct every rounds with y as its center and r (the length of the rod) as its radius. The sectors, parts of the rounds that locate between obstacles 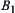 and
and 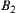 , are non-empty. And the sector is at a distance from the rest of obstacles except
, are non-empty. And the sector is at a distance from the rest of obstacles except 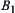 and
and 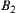 . Thus, the arc corresponding to the sector is a connected component of
. Thus, the arc corresponding to the sector is a connected component of 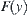 denoted by
denoted by 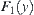 satisfying
satisfying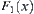 is continuous at x.
is continuous at x.
![]()
For each component 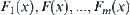 of
of 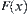 , we conduct the same analysis and obtain that when x changes from
, we conduct the same analysis and obtain that when x changes from 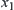 to
to 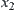 in
in 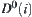 continuously, each component
continuously, each component 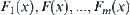 will change from
will change from 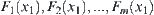 to
to 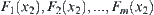 continuously, respectively. Thus,
continuously, respectively. Thus, 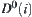 is a homotopically equivalent class.
is a homotopically equivalent class.
The Construction of Characteristic Network
(1) Domain 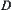 is divided into several connected regions by the original boundaries, r-growing boundaries of obstacles, and the boundaries of the shaded areas. The connected regions are denoted by
is divided into several connected regions by the original boundaries, r-growing boundaries of obstacles, and the boundaries of the shaded areas. The connected regions are denoted by 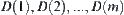 .
.
(2) To find the components of 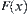 on each region
on each region 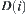 , it only needs to find the components of
, it only needs to find the components of 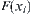 for any
for any 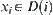 . Then, we have a set
. Then, we have a set 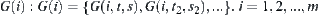 of components.
of components.
Where, 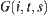 denotes the image of component
denotes the image of component 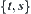 of
of 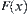 on
on 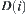 , and component
, and component  represents the component lied between edges
represents the component lied between edges  and
and 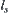 .
.
(3) Node 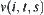 is constructed with respect to each
is constructed with respect to each 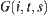 . We have a set V of nodes.
. We have a set V of nodes.
Assume that 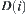 and
and 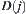 are neighboring. According to different forms of their common edge, there are four different linking rules.
are neighboring. According to different forms of their common edge, there are four different linking rules.
(a) 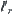 is their common edge, where
is their common edge, where 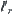 is the r-growing boundary of edge
is the r-growing boundary of edge 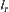 . Assume that
. Assume that 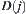 is on the inside of
is on the inside of 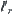 , i.e.,
, i.e., 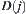 is located between
is located between 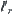 and
and 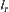 . Then
. Then 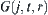 and
and 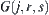 in
in  are linked with
are linked with 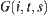 in
in 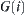 .
.
(b) 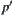 is their common edge, where
is their common edge, where 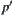 is a r-growing boundary of vertex p.
is a r-growing boundary of vertex p. 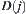 is on the inside of
is on the inside of 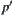 . Then
. Then 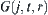 and
and 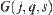 in
in 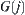 are linked with
are linked with 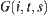 in
in 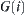 .
.
If p is a concave vertex, i.e., the angle corresponding to vertex p is greater than 180, then 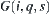 in
in 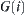 is not linked with any
is not linked with any 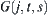 in
in 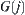 .
.
(c) If s is their common edge, where s is the boundary of the shaded area corresponding to lane 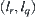 and
and 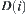 is on the inside of s, then
is on the inside of s, then 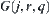 in
in 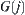 is not linked with any
is not linked with any 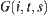 in
in 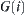 .
.
(d) 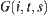 in
in 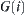 is linked with
is linked with 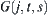 in
in 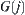 , i.e., the components with the same name in
, i.e., the components with the same name in 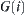 and
and 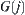 .
.
Based on the preceding rules, linking the nodes in the set V, we have a network 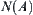 .
. 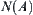 is the characteristic network corresponding to the rod A.
is the characteristic network corresponding to the rod A.
Examples
Example 5.8
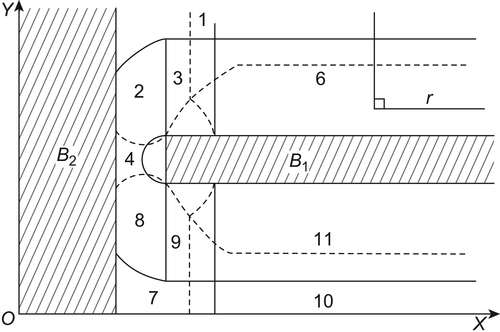
The obstacles are shown in Fig. 5.32. Find the characteristic network of rod OT.
Solution
D is divided into 13 regions shown in Fig. 5.32. Taking the number of each region 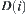 as the horizontal ordinate, and the number (double index) of each component as the vertical ordinate, if
as the horizontal ordinate, and the number (double index) of each component as the vertical ordinate, if 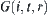 exists, and then we draw a node
exists, and then we draw a node 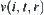 in the point where the horizontal ordinate is i and the vertical ordinate is
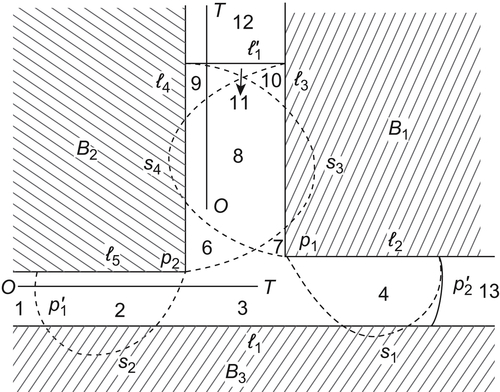
in the point where the horizontal ordinate is i and the vertical ordinate is 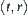 . Then, we have the characteristic network as shown in Fig. 5.33.
. Then, we have the characteristic network as shown in Fig. 5.33.
If  , the boundary of shaded area, is the common edge of
, the boundary of shaded area, is the common edge of 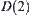 and
and 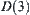 , then
, then 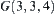 is not linked with any point in
is not linked with any point in 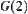 , according to the rule.
, according to the rule.
If 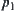 is the common edge of
is the common edge of 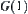 and
and 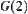 , where the two included sides of
, where the two included sides of  are
are 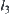 and
and 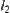 , then
, then 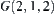 and
and 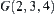 are linked with
are linked with 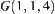 , according to the rule. But
, according to the rule. But 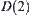 is on the inside of
is on the inside of 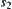 , component
, component 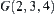 disappears. Finally,
disappears. Finally, 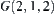 is connected to
is connected to 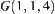 . Moreover,
. Moreover, 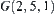 is connected to
is connected to 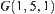 with the same name.
with the same name.
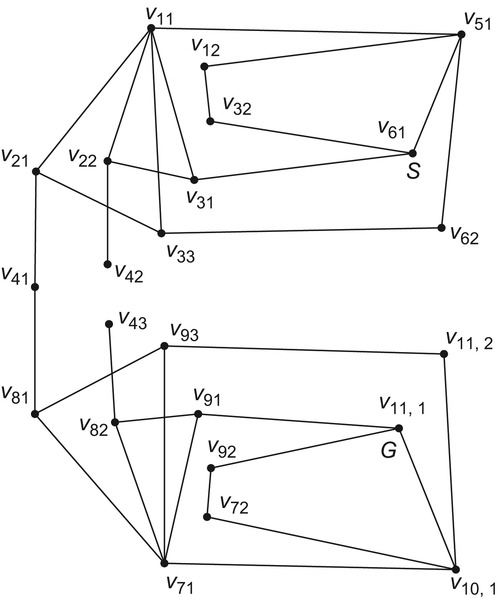
The same rules are applied to other components. Finally, the characteristic network we obtained is shown in Fig. 5.33.
From Fig. 5.33, we can see that the characteristic network consists of three disconnected sub-networks. This implies that rod OT can't move from a state to an arbitrary state, e.g., from state 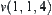 rod OT can't move to state
rod OT can't move to state 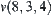 , since there is no connected path from node
, since there is no connected path from node 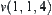 to node
to node 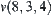 in the network (Fig. 5.33).
in the network (Fig. 5.33).
Example 5.9
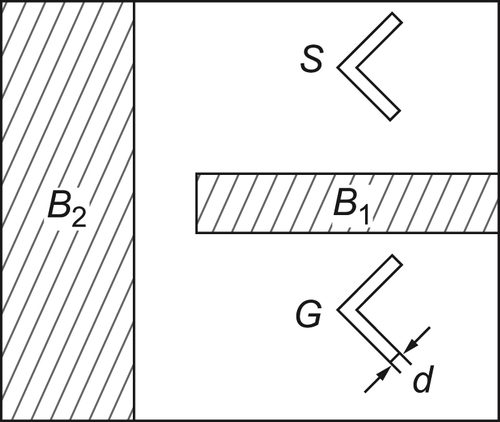
The ‘Piano Mover’ problem is that given a ‘piano’ A and the obstacles as shown in Fig. 5.34, find a path from the initial position S to the goal position G.
For simplicity, piano A is shrunk to a broken-line while the boundaries of obstacles B1 and B2 are enlarged by the size 1/2 d, where d is the width of the piano A.
Its characteristic network is shown in Fig. 5.36.
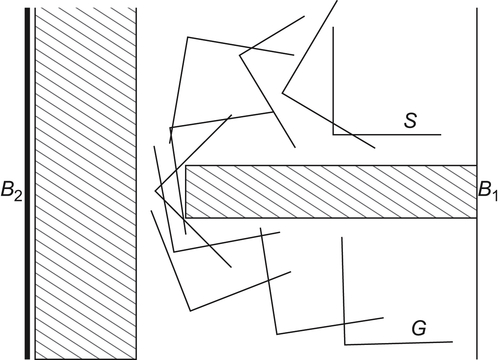
The final result implemented by computers is shown in Fig. 5.37.
5.5.2. Motion Planning for a Multi-Joint Arm
Multi-Joint Arm
The rotation angle about 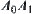 is denoted by
is denoted by 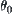 . The rotation angle of each arm
. The rotation angle of each arm 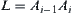 around
around 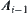 is represented by
is represented by 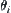 . The length of arm Li is
. The length of arm Li is 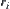 . The obstacles are assumed to be composed by a finite number of convex polyhedrons.
. The obstacles are assumed to be composed by a finite number of convex polyhedrons.
The problem is to find a collision-free path for the arm from the initial position to the goal position.
Rotation Mapping
Assume that 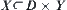 is the state space of a moving object and
is the state space of a moving object and 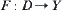 is its rotation mapping. X is assumed to be compact. In fact, when D and Y are the subsets of Euclidean space, so long as X is bounded and closed X is compact.
is its rotation mapping. X is assumed to be compact. In fact, when D and Y are the subsets of Euclidean space, so long as X is bounded and closed X is compact. 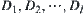 are the homotopically equivalent classes of D.
are the homotopically equivalent classes of D. 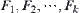 are the connected decompositions of F.
are the connected decompositions of F.
Let 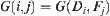 be the image of component
be the image of component 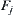 on
on 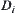 .
.
Some properties of the image of the rotation mapping are given below.
Proposition 5.9
F is a mapping from 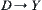 .
. 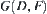 is the image of F. Assume that
is the image of F. Assume that 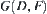 is compact and
is compact and 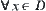 ,
, 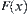 has a finite number of connected components. Let
has a finite number of connected components. Let 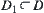 be a homotopically equivalent class of F.
be a homotopically equivalent class of F. 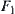 is a connected component of F on
is a connected component of F on 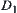 . Then we have that
. Then we have that 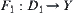 is semi-continuous.
is semi-continuous.
Proof
Let 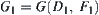 and
and 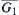 be the closure of
be the closure of 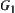 . Let
. Let 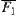 be a mapping corresponding to
be a mapping corresponding to 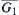 . Since
. Since 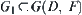 ,
, 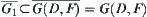 .
. 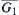 is a closed subset of the compact set
is a closed subset of the compact set 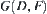 .
. 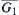 is also compact. From Theorem 5.4, we have that
is also compact. From Theorem 5.4, we have that 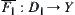 is semi-continuous.
is semi-continuous.
Again, 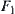 is a connected component of F on
is a connected component of F on  . So
. So  is a closed set on
is a closed set on 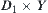 , i.e.,
, i.e., 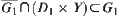 . We have
. We have 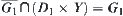 .
.
Namely, 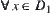 , have
, have 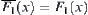 . We conclude that
. We conclude that 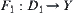 is semi- continuous.
is semi- continuous.
Definition 5.19
Corollary 5.3
If 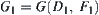 and
and 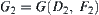 are regular neighboring, by letting
are regular neighboring, by letting 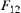 be the union mapping of
be the union mapping of 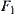 and
and 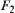 , then
, then 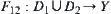 is semi-continuous.
is semi-continuous.
Proposition 5.10
Under the same assumption of Corollary 5.3, by letting 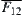 be a mapping corresponding to
be a mapping corresponding to 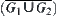 , and
, and 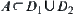 be a connected subset, then
be a connected subset, then 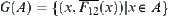 is a connected set.
is a connected set.
Proof
From Corollary 5.3 and dimension reduction principle, it now only needs to prove that 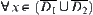 ,
, 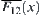 is connected.
is connected.
From the definition of the homotopically equivalent class, it easy to show that 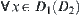 ,
, 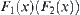 is connected. We now show that
is connected. We now show that 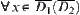 ,
, 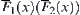 is connected.
is connected.
By reduction to absurdity, assume that for 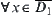 ,
, 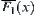 is not connected. Since
is not connected. Since 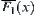 is compact, there exists
is compact, there exists 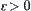 such that
such that 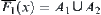 , where
, where  and
and 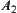 are non-empty,
are non-empty,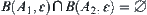 , and
, and 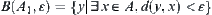 .
.
Since 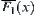 is semi-continuous, there exists
is semi-continuous, there exists 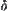 ,
, 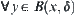 such that
such that
![]()
We obtain
![]()
However, 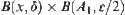 and
and 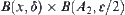 are separated sets. Again, it is known that
are separated sets. Again, it is known that 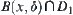 is connected.
is connected. 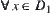 ,
, 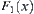 is connected and
is connected and 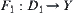 is semi-continuous. Thus,
is semi-continuous. Thus, 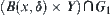 is a connected set, so it can only belong to either
is a connected set, so it can only belong to either 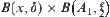 or
or 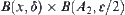 .
.
Assume 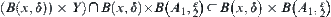 , i.e.,
, i.e., 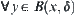 , we have
, we have 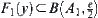 . Hence,
. Hence, 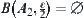 . This is in contradiction with the assumption. We have that
. This is in contradiction with the assumption. We have that 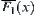 is connected.
is connected.
Similarly, 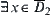 ,
, 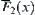 is connected.
is connected.
Similarly,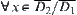 , we have
, we have 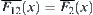 . Therefore,
. Therefore, 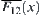 is connected as well.
is connected as well.
When 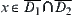 , since
, since 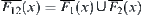 and
and 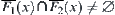 , we have that
, we have that 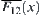 is connected.
is connected.
Finally, since 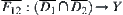 is semi-continuous and A is a connected set, from the dimension reduction theorem, we conclude that
is semi-continuous and A is a connected set, from the dimension reduction theorem, we conclude that 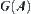 is connected.
is connected.
From the proposition, we can see that if two images 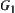 and
and 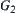 are regular neighboring, then the problem of considering the connectivity of
are regular neighboring, then the problem of considering the connectivity of 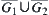 can be transformed into that of the connectivity of
can be transformed into that of the connectivity of 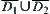 . If
. If 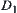 and
and 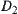 are regular neighboring, then the connectivity of
are regular neighboring, then the connectivity of 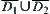 can also be transformed into that of still lower dimensional space. This is just the principle of dimension reduction.
can also be transformed into that of still lower dimensional space. This is just the principle of dimension reduction.
Characteristic Network
(1) 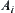 is the end point of a robot arm. All possible positions of
is the end point of a robot arm. All possible positions of 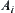 among obstacles are called the domain of
among obstacles are called the domain of 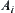 denoted by
denoted by 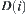 .
.
(2) 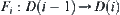 is a mapping,
is a mapping, 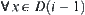 ,
, 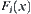 denotes all possible positions of the end point
denotes all possible positions of the end point 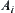 of arm
of arm 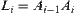 among obstacles, when the other end point
among obstacles, when the other end point 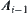 is located at x.
is located at x.
In fact, 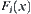 is the rotation mapping of x. The only difference is that
is the rotation mapping of x. The only difference is that 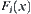 is represented by the positions of
is represented by the positions of 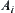 rather that the rotation angle
rather that the rotation angle 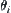 .
. 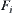 is the rotation mapping of the robot arm on
is the rotation mapping of the robot arm on  .
.
Let 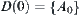 . i.e.,
. i.e., 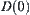 is a point
is a point 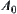 .
.
If 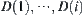 have been defined, then we define
have been defined, then we define 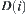 as follows.
as follows.
(3) The connected decomposition mapping 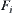 .
.
Assume that the connected decomposition sub-mapping 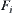 on
on 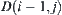 is
is 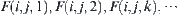 .
.
The image of 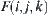 on
on 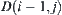 is
is 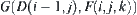 denoted by
denoted by 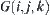 . Moreover, let each pair
. Moreover, let each pair 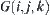 of neighboring images be regular neighboring.
of neighboring images be regular neighboring.
When the moving object is a polyhedron and the obstacles consist of a finite number of polyhedrons, the homotopically equivalent set decomposition of D and the connected decomposition of F will make the neighboring images 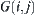 become regular neighboring.
become regular neighboring.
(4) Characteristic network of arm 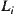
Using the same method presented in Section 5.4.2, we have the characteristic network of 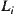 denoted by
denoted by 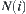 .
.
The Construction of Characteristic Network
Assume that 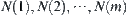 are characteristic networks corresponding to
are characteristic networks corresponding to 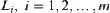 , respectively.
, respectively.
We compose a product set 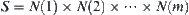 .
.
Let 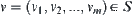 and
and 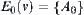 .
.
Assuming that 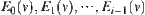 have been obtained, we define
have been obtained, we define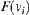 is a connected component with respect to point
is a connected component with respect to point 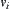 ,
, 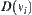 is a domain corresponding to
is a domain corresponding to 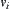 .
.
![]()
![]()
Definition 5.20
Given 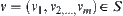 , if
, if 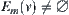 then v is a node of characteristic network
then v is a node of characteristic network 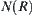 , i.e., we have a set V of nodes,
, i.e., we have a set V of nodes, 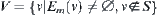 .
.
Definition 5.21
Given 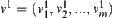 and
and 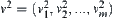 , where
, where 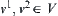 .
. 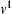 and
and 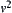 are called neighboring if and only if
are called neighboring if and only if 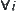 ,
, 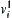 and
and 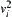 are neighboring in
are neighboring in  .
.
Linking each pair of neighboring nodes in V with a line, we have a network  , or N for short. It is called a characteristic network of a multi-joint arm R.
, or N for short. It is called a characteristic network of a multi-joint arm R.
Next, an example of motion planning for a 3D manipulator is shown below.
Example 5.10
A manipulator and its environment are shown in Fig. 5.39. The initial and final configurations are shown in Fig. 5.39(a) and Fig. 5.39(b), respectively. Based on the dimension reduction principle, we have developed a path planning program for a three-joint arm among the obstacles composed by a finite number of polyhedrons and spheres, using C language. The program has been implemented on SUN 3/260 workstation. One of the results is shown in Fig. 5.39. The CPU time for solving the problem is 5–15 seconds in average.
5.5.3. The Applications of Multi-Granular Computing
In motion planning for a multi-joint arm, the concept of multi-granular computing has been used for solving several problems.
In the construction of characteristic network 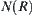 , we regard
, we regard 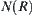 as a subset of the product set
as a subset of the product set 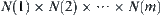 . To find a connected path from the initial state
. To find a connected path from the initial state 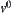 to the final state
to the final state 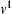 in
in 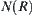 , a connected path from
, a connected path from 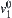 to
to 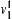 in
in 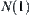 is found first, then a connected path from
is found first, then a connected path from 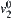 to
to 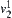 in
in 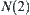 is found such that the path merged from these two is a connected path from
is found such that the path merged from these two is a connected path from 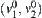 to
to 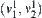 in the product space
in the product space 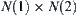 . The process continues until a connected path from
. The process continues until a connected path from 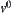 to
to 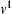 is found, or the existence of collision-free paths is disproved.
is found, or the existence of collision-free paths is disproved.
This is a typical application based on multi-granular computing. Since 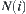 is the projection of
is the projection of 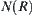 , however, ‘projection’ is one of the multi-granular computing approaches as mentioned in the above chapters.
, however, ‘projection’ is one of the multi-granular computing approaches as mentioned in the above chapters.
The dimension reduction method itself is an application based on the multi-granular computing technique as well. The original problem of finding the connected structure of a set 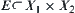 is transformed to that of finding the connected structure of
is transformed to that of finding the connected structure of 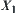 and
and 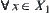 ,
, 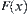 , where F is a mapping corresponding to E. Since
, where F is a mapping corresponding to E. Since 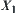 and
and 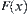 both are the projections of E on different spaces, the multi-granular computing technique underlies the dimension reduction method.
both are the projections of E on different spaces, the multi-granular computing technique underlies the dimension reduction method.
In the proceeding applications, the multi-granular computing technique is used mainly through the projection method. Next, other methods are discussed.
The Hierarchical Planning of a Multi-Joint Arm
R is a multi-joint planar manipulator composed of m arms. To find a collision-free path from state 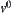 to state
to state 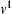 among the obstacles, the motion planning can be made in the following way. First, a primary plan is found by some heuristic knowledge. Then, the plan is refined.
among the obstacles, the motion planning can be made in the following way. First, a primary plan is found by some heuristic knowledge. Then, the plan is refined.
As shown in Fig. 5.40, R is a multi-joint arm moving among the planar environment consisting of obstacles 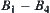 .
.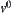 and
and 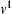 are the initial and final positions of R, respectively.
are the initial and final positions of R, respectively.
To plan the primary path, we compose a loop from 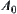 along the direction
along the direction 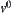 . i.e.,
. i.e.,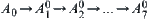 , then from
, then from 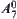 to
to 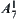 , finally from
, finally from 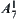 along the direction
along the direction 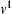 back to
back to 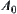 . i.e.,
. i.e., 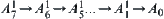 . If there is no obstacle inside the loop, then the manipulator can ‘move’ from
. If there is no obstacle inside the loop, then the manipulator can ‘move’ from 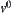 to
to 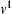 directly without collision. Therefore, in this case only a limited portion of N(r) needs searching in order to find the path.
directly without collision. Therefore, in this case only a limited portion of N(r) needs searching in order to find the path.
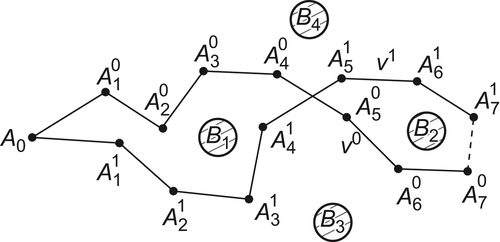
If there are obstacles inside the loop, as shown in Fig. 5.40, obstacles 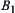 and
and 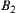 are inside the loop. Then, to move the manipulator around the obstacles, the initial positions of end points
are inside the loop. Then, to move the manipulator around the obstacles, the initial positions of end points 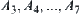 of each arm must first move from
of each arm must first move from 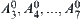 to the left of obstacle
to the left of obstacle 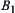 . In other words, from a high abstraction level, we first estimate the primary moving path of R by ignoring the interconnection between arms. Namely, the end point
. In other words, from a high abstraction level, we first estimate the primary moving path of R by ignoring the interconnection between arms. Namely, the end point 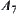 of arm 7 first moves along the direction
of arm 7 first moves along the direction 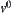 from
from 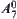 to the left of obstacle
to the left of obstacle 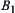 , i.e., point
, i.e., point 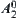 , then moves to
, then moves to 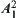 , finally moves to
, finally moves to 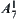 along the direction
along the direction 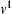 .
.
End points 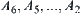 move in a similar way.
move in a similar way.
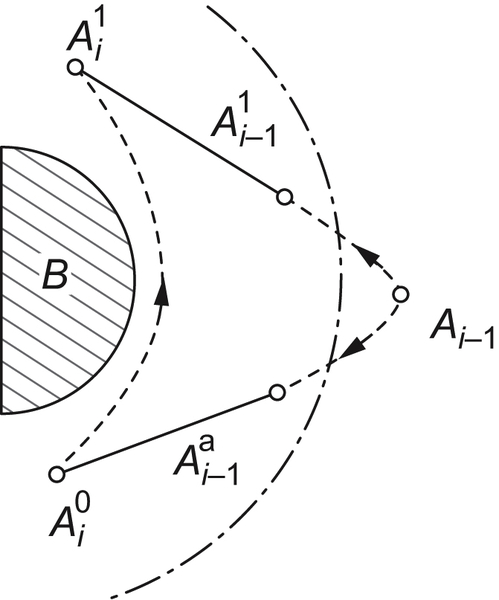
If the end point 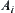 of arm
of arm 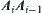 needs to move from one side of obstacle B to the other (Fig. 5.41), then the end point Ai−1 must move from the inside of the r-growing boundary to the outside of the boundary and then back to the inside of B. Namely, the moving trajectory of point
needs to move from one side of obstacle B to the other (Fig. 5.41), then the end point Ai−1 must move from the inside of the r-growing boundary to the outside of the boundary and then back to the inside of B. Namely, the moving trajectory of point 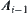 is constrained by the trajectory of point
is constrained by the trajectory of point 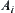 .
.
By using these kinds of heuristic information, the primary moving path of R can be worked out. Then under the guidance of the primary path, a final path can be found.
In three-dimensional case, some proper sections can be used. The two-dimensional characteristic networks can be constructed on these sections. By using the neighboring relationship between the nodes on the neighboring two-dimensional characteristic networks, the characteristic network of the three-dimensional case can be constructed.
As shown in Fig. 5.42(a), we construct the sections 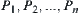 . Let
. Let 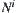 be the two-dimensional characteristic network on section
be the two-dimensional characteristic network on section 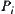 .
.
If 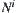 on
on 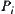 is a connected network,
is a connected network, 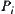 is said to be a connected section. Therefore, when net
is said to be a connected section. Therefore, when net 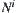 is a connected one, section
is a connected one, section 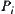 does not intersect with any obstacle.
does not intersect with any obstacle.
Assume that 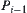 and
and 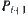 are two neighboring sections of
are two neighboring sections of 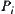 . If one of
. If one of 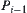 and
and 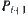 is a connected section, then when finding a connected path from state
is a connected section, then when finding a connected path from state 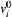 to
to 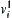 on
on 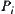 , we first transform the state
, we first transform the state 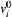 to a state
to a state 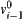 on
on 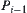 , then on
, then on 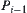 move state
move state 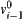 to state
to state 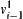 . Finally,
. Finally, 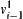 is transformed to state
is transformed to state 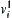 on
on 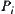 .
.
Thus, the three-dimensional case can be handled in the similar way as in the two- dimensional case.
5.5.4. The Estimation of the Computational Complexity
Schwartz and Shatic (1983a) presented a topologic algorithm for two-dimensional path planning. Its computational complexity is 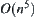 , where n is the number of edges of polygonal obstacles. Schwartz and Shatic (1983b) also presented a topologic algorithm for solving ‘piano-mover’. Its computational complexity is
, where n is the number of edges of polygonal obstacles. Schwartz and Shatic (1983b) also presented a topologic algorithm for solving ‘piano-mover’. Its computational complexity is 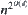 , where n is the number of obstacles and d is the degree of freedom of moving object.
, where n is the number of obstacles and d is the degree of freedom of moving object.
Reif (1979) and Reif and Sharir (1985) presented a revised algorithm. Its complexity is 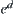 , and proved that the general ‘piano-mover’ is a PSPACE-hard problem, i.e., NP-hard problem at least.
, and proved that the general ‘piano-mover’ is a PSPACE-hard problem, i.e., NP-hard problem at least.
In a word, the complexity of collision-free paths planning increases with d exponentially even though by using topologic approaches.
Next, we estimate the complexity of the dimension reduction method by taking motion planning for a planar rod as an example.
Fig. 5.42(a) shows a rod AT and its environment. When the end point A of rod AT moves from the initial state 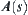 , there are three possible moving directions, i.e.,
, there are three possible moving directions, i.e.,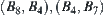 and
and 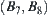 , or (8, 4), (4, 7) and (7, 8) for short, as shown in Fig. 5.42(b). There is no path along the direction (7, 8). Along the direction (8, 4), from point 1 there are two possible moving direction (8, 1) and (1, 4). Along direction (1, 4), from point 2 there also exist two possible moving directions (1, 2) and (2, 4). But direction (2, 4) is a blind alley, etc. We finally have a network shown in Fig. 5.42 (c). It is called a characteristic network of point A denoted by
, or (8, 4), (4, 7) and (7, 8) for short, as shown in Fig. 5.42(b). There is no path along the direction (7, 8). Along the direction (8, 4), from point 1 there are two possible moving direction (8, 1) and (1, 4). Along direction (1, 4), from point 2 there also exist two possible moving directions (1, 2) and (2, 4). But direction (2, 4) is a blind alley, etc. We finally have a network shown in Fig. 5.42 (c). It is called a characteristic network of point A denoted by 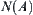 .
.
Network 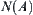 represents the connected structure of the domain of point A. Each edge
represents the connected structure of the domain of point A. Each edge 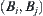 represents an area surrounded by obstacles
represents an area surrounded by obstacles 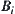 and
and 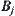 .
.
Based on network 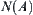 , the movement of rod AT among obstacles can be planned.
, the movement of rod AT among obstacles can be planned.
Although point A can move freely along each edge of 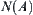 , rod AT may not. For example, when AT moves from point 1 to 3 through point 2, i.e., turns from direction
, rod AT may not. For example, when AT moves from point 1 to 3 through point 2, i.e., turns from direction 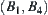 to direction
to direction 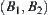 , if we consider the entire rod movement, the movement may not be possible at the intersecting point. Therefore, we must consider the movement at each intersecting point.
, if we consider the entire rod movement, the movement may not be possible at the intersecting point. Therefore, we must consider the movement at each intersecting point.
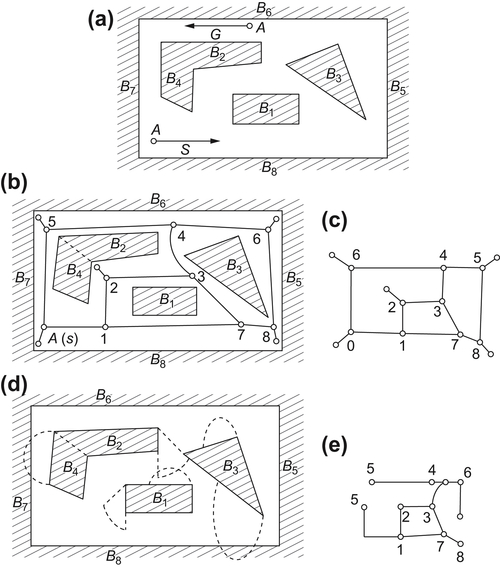
Whether rod AT can turn from one direction to the other may be judged by finding the boundary of the shaded area, presented in the above sections. In the example, the boundaries of each shaded area are shown in Fig. 5.43(d) by the dotted lines.
From Fig. 5.43(d), we can see that turning from direction (4, 7) to (2, 6), from (8, 3) to (5, 3), or from (3, 2) to (6, 2) is impossible. The others are possible. The characteristic network is shown in Fig. 5.43(e).
Given the initial state corresponding to direction (8,4) and goal state corresponding to direction (6,2), we now plan a collision-free path. From (8,4) we search the collision-free paths as shown below.
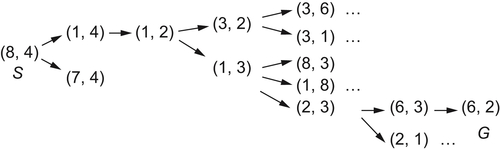
Next, we estimate its computational complexity.
Assume there are n convex polygons. By using the concept of dual network and the Euler formula concerning the relationship between points and edges of a planar network, it can be proved that the number of edges in network 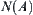 is less than or equal to cn, where c is a constant.
is less than or equal to cn, where c is a constant.
Each edge in 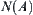 represents a direction
represents a direction 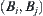 , or a ‘channel’ surrounded by obstacles
, or a ‘channel’ surrounded by obstacles 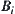 and
and 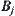 . Strictly speaking, if
. Strictly speaking, if 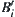 and
and 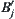 are r-growing areas of obstacles
are r-growing areas of obstacles 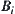 and
and 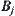 , respectively, then
, respectively, then 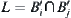 is the channel surrounded by
is the channel surrounded by 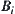 and
and 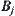 .
.
To make the turn from the channel 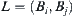 to channel
to channel 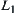 possible, the necessary condition is that
possible, the necessary condition is that 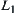 must intersect the r-growing area of
must intersect the r-growing area of 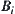 or
or 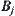 , i.e., the channel corresponding to edge
, i.e., the channel corresponding to edge 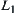 on
on 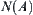 intersects
intersects 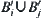 , where
, where 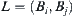 is an edge of N (A),
is an edge of N (A), 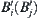 is the r-growing boundary of
is the r-growing boundary of 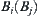 . If the complexity of each judgment is regarded as 1, we have the following proposition.
. If the complexity of each judgment is regarded as 1, we have the following proposition.
Proposition 5.12
If the environment consists of n convex polygons, the computational complexity for planning the motion of two-dimensional moving rod is 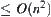 , if using the above hierarchical planning method.
, if using the above hierarchical planning method.
Certainly, this is just a rough estimation. It is shown that the multi-granular computing strategy has a potential in reducing the computational complexity.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.