1.4. The Relation Among Different Grain Size Worlds
Generally, we treat a problem under various grain sizes. Thus, it is necessary to establish the relationship between the worlds at different granularities.
1.4.1. The Structure of Multi-Granular Worlds
Semi-Order Lattice
Proposition 1.2
Under the relation ‘<’ defined in Definition 1.8, the family of quotient sets corresponding to 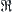 , or simply
, or simply 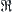 , is a complete semi-order lattice.
, is a complete semi-order lattice.
Note: Definition of complete semi-order lattice (Davey and Priestley, 1992) is the following.
A semi-order relation ‘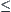 ’ is defined on X (X may be infinite).
’ is defined on X (X may be infinite). 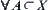 , if A has the supremum and infimum, i.e., there exist
, if A has the supremum and infimum, i.e., there exist  , for
, for 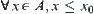 if
if 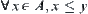 , then
, then 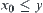 (supremum) and there exist
(supremum) and there exist 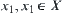 , for
, for 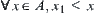 if
if 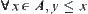 , then
, then 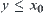 (infimum), then
(infimum), then 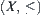 is called a complete semi-order lattice.
is called a complete semi-order lattice.
Proof:
For a family  of relations, define
of relations, define 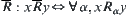 .
.
Now we prove that 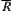 is the supremum of
is the supremum of 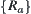 below.
below.
First, we show that 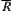 is an equivalence relation. Its reflexivity and symmetry are obvious.
is an equivalence relation. Its reflexivity and symmetry are obvious.
We show its transitivity. Assume 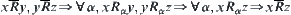 . Assume that R satisfies
. Assume that R satisfies 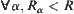 . Then,
. Then, 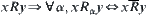 , i.e.,
, i.e., 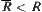 . Thus,
. Thus, 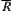 is the supremum.
is the supremum.
Now we prove that 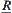 is the infimum of
is the infimum of 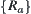 below.
below.
First, we show that 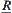 is an equivalence relation. From the definition of
is an equivalence relation. From the definition of 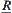 , its reflexivity and symmetry are obvious.
, its reflexivity and symmetry are obvious.
From 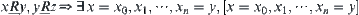 and
and
Now we show that 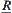 is the infimum. Assume that R is any lower bound of
is the infimum. Assume that R is any lower bound of 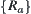 , i.e., for
, i.e., for 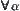 ,
, 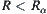 . Assume
. Assume 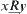 , i.e.,
, i.e., 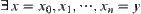 such that
such that 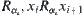 ,
, 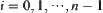 . From
. From 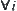
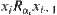 and
and  , we have
, we have  .
.
From its transitivity, we have that 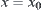 and
and 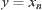 are R equivalent, i.e.,
are R equivalent, i.e., 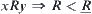 . Again,
. Again,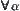 ,
, 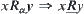 , then
, then 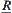 is the infimum.
is the infimum.
Finally, 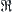 is a complete semi-order lattice.
is a complete semi-order lattice.
Obviously, when 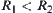 ,
,  is a quotient set of
is a quotient set of 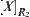 , where
, where 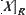 is a quotient set of X corresponding to equivalence relation R. The proposition shows that given a domain X, all its quotient sets compose a complete semi-order lattice based on the inclusion relations of the sets. We can implement various supremum and infimum operations over the lattice.
is a quotient set of X corresponding to equivalence relation R. The proposition shows that given a domain X, all its quotient sets compose a complete semi-order lattice based on the inclusion relations of the sets. We can implement various supremum and infimum operations over the lattice.
In Fig. 1.3, if under the equivalence relation R0, the whole factory is regarded as an equivalence class, i.e., all elements of X are equivalent, then 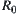 is the coarsest relation among R. If the factory is decomposed into several equivalence classes such as machining, assembly and welding workshops, etc., we have a new equivalence relation
is the coarsest relation among R. If the factory is decomposed into several equivalence classes such as machining, assembly and welding workshops, etc., we have a new equivalence relation 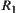 . Similarly, each workshop can be further divided into fine-grained cells, and so on. Finally, we have
. Similarly, each workshop can be further divided into fine-grained cells, and so on. Finally, we have 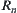 such that
such that 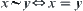 . This means that
. This means that 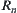 is the finest relation among R. And we have
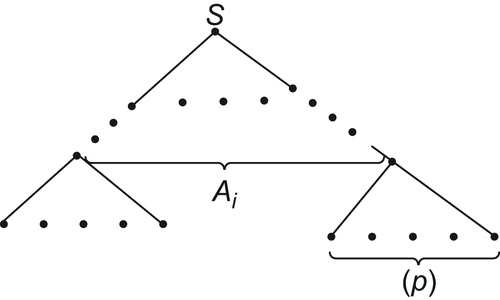
is the finest relation among R. And we have be a node of G.
be a node of G. 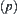 denotes all leaves of the subtree rooted at p. Let
denotes all leaves of the subtree rooted at p. Let 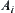 be a set of nodes at depth i. Then each Ai corresponds to a partition of X, i.e., for
be a set of nodes at depth i. Then each Ai corresponds to a partition of X, i.e., for 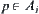 ,
, 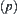 is an equivalence class and corresponds to an equivalence relation
is an equivalence class and corresponds to an equivalence relation 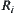 .
.
![]()
Obviously,  .
.
Conversely, a sequence of monotonic relations  can be represented by a tree with n levels.
can be represented by a tree with n levels.
If a function f (x) is assigned to each leaf  , then a heuristic search of G can be regarded as a hierarchical inference over a sequence of monotonic equivalence relations, that is, a heuristic tree search can be transformed into a hierarchical problem solving. We will further discuss it in Chapter 6.
, then a heuristic search of G can be regarded as a hierarchical inference over a sequence of monotonic equivalence relations, that is, a heuristic tree search can be transformed into a hierarchical problem solving. We will further discuss it in Chapter 6.
1.4.2. The Structural Completeness of Multi-Granular Worlds
In Section 1.4.1, we show the structural completeness of a family of quotient sets, i.e., given domain X, all equivalence relations defined on X compose a complete semi-order lattice. This is a structural completeness theorem of a family of quotient sets. We’ll extend the theorem to a family of quotient spaces, i.e., the structural completeness theorem of multi-granular worlds.
We’ll discuss the properties of three different complete lattice structures in a family of quotient spaces. And we’ll show that the three complete lattice structures correspond to the closures of three main operations on quotient-based granular computing, respectively.
Definition 1.9
Basic Theorem (Completeness Theorem)
Under the relation ‘<’ defined in Definition 1.9, the family of quotient spaces corresponding to 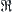 , or simply
, or simply 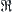 , composes a complete semi-order lattice.
, composes a complete semi-order lattice.
Compared to other methods such as rough set theory, quotient space theory pays more extension to the concept of ‘structures’. So it is needed to investigate families of all quotient spaces composed from topologic space 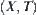 and to establish the corresponding structural theorem. We will establish three different complete lattice structures of families of quotient spaces and their properties, relations and applications below.
and to establish the corresponding structural theorem. We will establish three different complete lattice structures of families of quotient spaces and their properties, relations and applications below.
1.4.2.1. The Basic Theorem of Families of Quotient Spaces
A topologic space 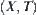 is given. Let
is given. Let 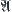 be a set of all possible quotient sets on X, and
be a set of all possible quotient sets on X, and  denotes its element.
denotes its element.
Definition 1.10
Assume  . If
. If  is a quotient set of
is a quotient set of 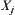 , then
, then 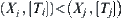 .
.
Theorem 1.1
Under the Definition 1.10, 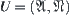 composes a complete semi-order lattice.
composes a complete semi-order lattice.
From the basic theorem, we have the theorem above.
If the topology on quotient sets is unrestricted, i.e., it is not limited to the quotient topology induced from quotient set, the theorem does not necessarily hold. This means that the supremum (or infimum) of a family of topologies is not a quotient topology induced from quotient set. Namely, there exists a subset of U such that it does not have the supremum (infimum) within U. The following example shows the fact.
Example 1.7
Topologic space 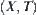 is given, where
is given, where 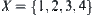 and
and 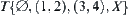 . Let
. Let 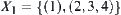 and
and 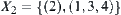 . We have
. We have 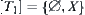 and
and 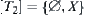 , the induced quotient topologies from
, the induced quotient topologies from 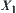 and
and 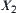 , respectively. Thus, their supremum topology
, respectively. Thus, their supremum topology 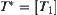 .
.
In the other hand, the supremum of 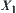 and
and 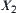 is
is 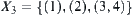 . The induced topology from X3 is
. The induced topology from X3 is  . Thus,
. Thus,  .
.
Definition 1.11
A topologic space 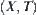 , if
, if 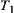 is another topology on X and
is another topology on X and 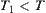 ,
, 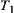 is called a ‘lower topology’ of T.
is called a ‘lower topology’ of T.
Definition 1.12
Assume 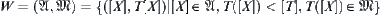 , where
, where 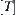 is a quotient topology on
is a quotient topology on 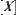 induced from
induced from 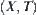 .
. 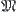 is a set of all lower topologies of T on X. Define a semi-order ‘<’ on
is a set of all lower topologies of T on X. Define a semi-order ‘<’ on 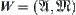 as follows:
as follows: 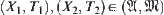 , if
, if 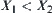 and
and 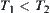 , then
, then 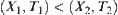 .
.
First, two lemmas are introduced below (Eisenberg, 1974).
Lemma 1.1
Assume that  . There exists a maximal (finest) topology among all topologies that makes each fa continuous on Y.
. There exists a maximal (finest) topology among all topologies that makes each fa continuous on Y.
Lemma 1.2
Assume that 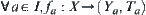 . There exists a minimal (coarsest) topology among all topologies that makes each
. There exists a minimal (coarsest) topology among all topologies that makes each  continuous on X.
continuous on X.
Definition 1.13
Given 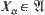 . Let
. Let 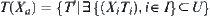 , where
, where 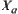 is the supremum (infimum) of
is the supremum (infimum) of 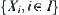 , T′ is the supremum (infimum) of
, T′ is the supremum (infimum) of 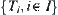 . Define
. Define
![]()
Definition 1.14
Definition 1.15
It’s noted that for any subset on V, based on Definitions 1.13 and 1.14 we can also define its corresponding supremum and infimum quotient spaces, respectively.
Theorem 1.2
Under the supremum and infimum operations defined by Definitions 1.13 and 1.14, V (or W) composes a complete semi-order lattice.
Proof:
First, we prove that W is a complete semi-order lattice.
Similarly, for any subset B, there exists its infimum. Therefore, W is a complete lattice.
Similarly, we can prove that V is a complete semi-order lattice.
Obviously, V is a sub-lattice of W and a complete lattice obtained by the supremum and infimum operations over elements of U. And W is a complete lattice composed by elements of U and all lower topologies of the induced quotient topologies on U.
1.4.2.2. The Properties and Relations of U, V and W
Complete semi-order set U is a basic quotient space structure in quotient space-based theory. Given a space 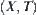 , using the induced quotient topology we can construct all quotient spaces of U. Conversely, a quotient space constructed by the induced quotient topology must be an element (space) of U. In other words, with respect to the operation of constructing quotient spaces by the induced quotient topology, U is closed. The completeness of U provides a theoretical foundation for the constructing quotient space method by induced quotient topology.
, using the induced quotient topology we can construct all quotient spaces of U. Conversely, a quotient space constructed by the induced quotient topology must be an element (space) of U. In other words, with respect to the operation of constructing quotient spaces by the induced quotient topology, U is closed. The completeness of U provides a theoretical foundation for the constructing quotient space method by induced quotient topology.
The combination method of quotient spaces is the main one in quotient space theory. V is the maximal complete lattice that can be produced by using the supremum and infimum operations over the induced quotient topologies of U. This is just a combination method of quotient spaces and similar to the method that quotient topologies are produced by topological bases. The supremum and infimum operations over induced quotient topologies of U are closed on V, which ensures the completeness of the family of quotient spaces that is produced by the combination method.
If the quotient spaces are not only constructed by domain granulation (quotient sets) but also by topology granulation in U, then we have W, the complete lattice composed by all possible quotient spaces from the above method and from the supremum and infimum operations over the quotient spaces.
In order to discuss the relation among U, V and W, we introduce the concept of ‘minimal open set’ below.
Definition 1.16
Given a topologic space 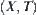 . For any open set B, if a non-empty bipartition
. For any open set B, if a non-empty bipartition  exists such that one of them is an open set at most, B is called a minimal open set.
exists such that one of them is an open set at most, B is called a minimal open set.
Lemma 1.3
For any open set A, it either a discrete topology or a minimal open set.
Proof:
Otherwise, assume that A is not a minimal open set. For 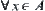 , constructing a non-empty bipartition
, constructing a non-empty bipartition  of A, since any singleton
of A, since any singleton 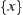 of A is an open set, A is a discrete topology.
of A is an open set, A is a discrete topology.
Obviously, 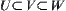 . We’ll prove below that in general the relation among U, V and W is a proper subset one. For example, in Section 1.4.2.1, quotient space
. We’ll prove below that in general the relation among U, V and W is a proper subset one. For example, in Section 1.4.2.1, quotient space 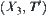 is in V but not in U, so U is a proper subset of V.
is in V but not in U, so U is a proper subset of V.
Theorem 1.3
Given a topologic space 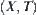 . The necessary and sufficient condition of U=V should satisfy one of the following conditions.
. The necessary and sufficient condition of U=V should satisfy one of the following conditions.
(1) 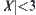
(2) T is a trivial topology
(3) T is a discrete topology.
Proof:
If 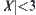 , obviously,
, obviously,  .
.
⇐ Sufficient condition: Since 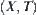 is a trivial (or discrete) topology, i.e., all quotient topologies on any quotient set
is a trivial (or discrete) topology, i.e., all quotient topologies on any quotient set  are trivial or discrete,
are trivial or discrete,  .
.
⇒Reduction to absurdity: Assume that T is neither a trivial nor a discrete topology. We show below that 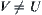 . Let
. Let 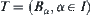 . From Lemma 1.3, for each
. From Lemma 1.3, for each 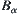 , a non-empty bipartition of
, a non-empty bipartition of 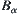 exists and one of its bipartition is an open set at most, i.e., a minimal open set. The open set is left, otherwise
exists and one of its bipartition is an open set at most, i.e., a minimal open set. The open set is left, otherwise 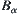 is divided into a set of singletons. After the treatment, T is denoted as
is divided into a set of singletons. After the treatment, T is denoted as 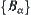 , where
, where 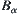 is either a singleton or a minimal open set.
is either a singleton or a minimal open set.
If T has only one component 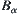 , then T is a trivial topology. This is a contradiction.
, then T is a trivial topology. This is a contradiction.
If each 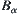 is a singleton, then T is a discrete topology. This is also a contradiction.
is a singleton, then T is a discrete topology. This is also a contradiction.
Thus, there exist some 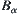 ’s such that
’s such that 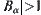 . Let
. Let 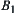 be the one having the minimal cardinality among
be the one having the minimal cardinality among 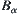 ’s. Now we discuss the following two cases.
’s. Now we discuss the following two cases.
(1) 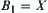 and any proper subset on X is not a minimal open set, then
and any proper subset on X is not a minimal open set, then 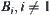 must be a singleton. Let
must be a singleton. Let 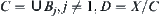 . Since
. Since 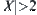 , there must exist a set in C and D with cardinality > 1. If
, there must exist a set in C and D with cardinality > 1. If 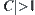 , construct a partition
, construct a partition 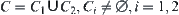 of C. We have a partition
of C. We have a partition  . Set D is not open, otherwise, from Lemma 1.3, D is a singleton. This is a contradiction. Set
. Set D is not open, otherwise, from Lemma 1.3, D is a singleton. This is a contradiction. Set 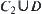 is not open as well, otherwise,
is not open as well, otherwise, 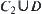 is a minimal open set. This is also a contradiction.
is a minimal open set. This is also a contradiction.
Then, we have induced quotient topologies 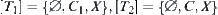 and the supremum topology
and the supremum topology 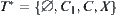 .
.
On the other hand, we have the supremum 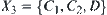 of
of 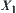 and
and 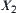 . Since
. Since 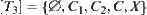 is the induced quotient topology from
is the induced quotient topology from  ,
, 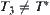 , then
, then 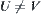 . This is a contradiction.
. This is a contradiction.
If C is a singleton, there exists a non-empty bipartition 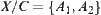 on
on  . Construct
. Construct 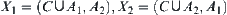 . Then,
. Then, 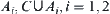 are not open. Otherwise, assume that
are not open. Otherwise, assume that 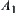 is an open set. From Lemma 1.3,
is an open set. From Lemma 1.3, 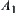 is either a discrete topology or a minimal open set. But the former is impossible since C is a singleton. The latter is impossible as well since
is either a discrete topology or a minimal open set. But the former is impossible since C is a singleton. The latter is impossible as well since 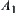 is a proper sunset of X. This is a contradiction. Therefore,
is a proper sunset of X. This is a contradiction. Therefore, 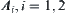 are not open sets.
are not open sets.
Similarly, 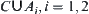 are not open sets either.
are not open sets either.
We have 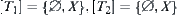 . Then
. Then 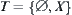 .
.
On the other hand, 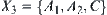 , we have
, we have  ,
,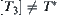
Then, 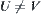 . This is a contradiction.
. This is a contradiction.
(2) 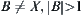 . Letting
. Letting 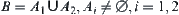 , there exists a
, there exists a 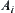 at least such that it is not an open set. Construct a partition
at least such that it is not an open set. Construct a partition 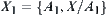 ,
, 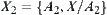 .
.
(2.1) If both  and
and 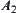 are not open sets, the induced quotient topology from
are not open sets, the induced quotient topology from 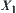 and
and 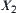 is
is 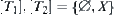 . The supremum of
. The supremum of 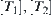 is
is 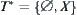 .
.
On the other hand, 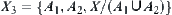 is the supremum of
is the supremum of  . The induced quotient topology is
. The induced quotient topology is 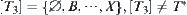 .
.
(2.2) If one of 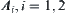 is an open set, in assuming that
is an open set, in assuming that 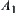 is an open set, then
is an open set, then 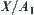 is not open. Otherwise,
is not open. Otherwise, 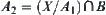 is open. This is a contradiction. Therefore, we have
is open. This is a contradiction. Therefore, we have 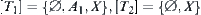 (or when
(or when 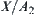 is an open set, we have
is an open set, we have 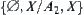 ). Its supremum is
). Its supremum is 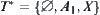 (or
(or 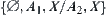 when
when 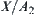 is open). Since
is open). Since 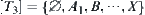 is the induced quotient topology of
is the induced quotient topology of 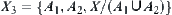 , we have
, we have 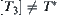 .
.
Finally, 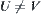 . This is a contradiction.
. This is a contradiction.
Using Theorem 1.3, we can make the following conclusion: a space may belong to lattice W but not to V.
Example 1.8
Given X={1,2,3,4}, T is a discrete topology. From Theorem 1.3, we have U and V corresponding to (X,T). Letting 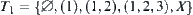 , we have
, we have 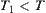 . Thus,
. Thus, 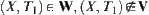 , V is a proper subset of W.
, V is a proper subset of W.
The three semi-order lattices given in the section correspond to three different multi-granular worlds. The completeness of the lattices provides a theoretical foundation for the translation, decomposition, combination operations over the multi-granular worlds.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
