2.4. Fuzzy Equivalence Relation and Hierarchy
In Chapter 1, we use the concept of quotient set in mathematics for establishing a multi-granular space. Our discussions have so far been limited to the partition of a domain so that each element belongs definitely to one and only one equivalence class. In reality, this is not always the case. Sometimes, the boundaries between two equivalence classes are not clear-cut. Two classes may have overlapped elements or their boundaries are fuzzy, i.e. the classification is fuzzy (Cheeseman, 1986; Nutter, 1987).
In clear-cut classification, we use equivalence relation R for establishing our model. A natural question is whether fuzzy equivalence relation can be used for constructing fuzzy classification model. We next try to do so. First, we introduce some concepts in fuzzy mathematics.
2.4.1. The Properties of Fuzzy Equivalence Relations
Definition 2.13
X is a domain. 
is a fuzzy set on X, that is, for 
there must exist a fixed number 
called a membership degree of x with respect to 
. The mapping 
or 
is called a membership function of 
.
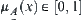is a fuzzy set on X, that is, for there must exist a fixed number called a membership degree of x with respect to 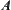. The mapping 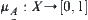or 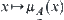is called a membership function of 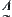.More simply, any function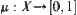 
defines a fuzzy subset on X. If 
is a set of all fuzzy subsets on X, then 
is a functional space consisting of all functions 
.
defines a fuzzy subset on X. If 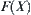is a set of all fuzzy subsets on X, then 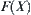is a functional space consisting of all functions .Definition 2.14
is a product space of X and X. For 
, 
is a fuzzy subset of 
, if it satisfies(1) 
(2) 
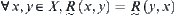
(3) 
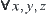, we have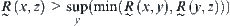 
, we have 
is called a fuzzy equivalence relation on X.If the value of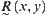 
only takes on 0 or 1, 
is just the common equivalence relation that we have discussed in the preceding sections. Thus, 
can be regarded as depicting the degree to which x and y are equivalent.
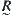only takes on 0 or 1, is just the common equivalence relation that we have discussed in the preceding sections. Thus, 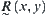can be regarded as depicting the degree to which x and y are equivalent.We now discuss the relationship between fuzzy equivalence relation and hierarchy.
Proposition 2.11
Assume that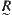 
is a fuzzy equivalence relation on X. If we define
is a fuzzy equivalence relation on X. If we define
Proof:
The reflexivity and symmetry of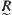 
are obvious. We now prove its transitivity.
are obvious. We now prove its transitivity.From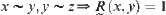 
and 
, we have
and 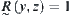, we have
Theorem 2.3
is a fuzzy equivalence relation on X. [X] is a quotient space as defined in Proposition 2.11. Define 
,
(2.10)
Then, 
is a distance function on [X].
is a distance function on [X].Proof:
First, we show that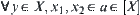 
, have 
.
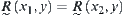, have .From the condition (3) in the definition of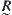 
, have
, have
Similarly,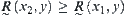 
.
.Then,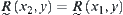 
.
.Therefore,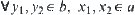 
and 
.
and .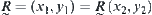
We show below that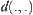 
is a distance function on [X].
is a distance function on [X].If 
, i.e., 
, we have
, i.e., 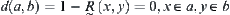, we have
Secondly, from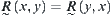 
, we have that d is symmetry.
, we have that d is symmetry.Finally,
is a distance function. 
is a metric space.
is a distance function. 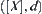is a metric space.The theorem shows that a fuzzy equivalence relation on X corresponds to a metric space on [X]. Then, a distance function on [X] can be used to describe the relation between two elements on X. The nearer the distance between two elements the closer their relation is. This means that any tool for analyzing metric spaces can be used to fuzzy equivalence relations.
Definition 2.15
is a fuzzy equivalence relation on X. Metric space 
defined in Theorem 2.3 is called a quotient structure space with respect to 
.Definition 2.16
is a fuzzy equivalence relation on X. Let
is a common equivalence relation on X, and is called a sectional relationship of 
.Let 
be a quotient space with respect to 
.
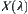be a quotient space with respect to 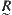.From the definition, we have the following property.
is a quotient set of 
.A family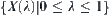 
of quotient spaces composes an order-sequence under the inclusion relation of quotient sets. 
forms a hierarchical structure on X. Thus, a fuzzy equivalence relation on X corresponds to a hierarchical structure on X.
of quotient spaces composes an order-sequence under the inclusion relation of quotient sets. 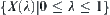forms a hierarchical structure on X. Thus, a fuzzy equivalence relation on X corresponds to a hierarchical structure on X.Theorem 2.3 states that from a fuzzy equivalence relation on X, a distance function can be defined on some quotient space [X]. Next, in Proposition 2.12, we will show conversely that from a distance function defined on [X], a fuzzy equivalence relation on X can be obtained. That is, a fuzzy equivalence relation on X is equivalent to a distance defined on [X].
First we introduce some basic concepts.
Definition 2.17
R is an equivalence relation on X. If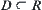 
satisfies: for 
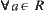there exist 
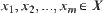such that 
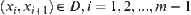and 
, then D is said to be a base of D.
satisfies: for there exist such that and 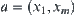, then D is said to be a base of D.Conversely, given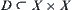 
and it satisfies for 
have (1) 
, and (2) 
. Again define 
there exist 
such that 
.
and it satisfies for 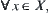have (1) 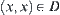, and (2) 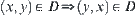. Again define 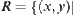there exist 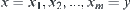such that .R is an equivalence relation on X, and is called an equivalence relation induced from D, or an equivalence relation with as D its base.
We next show that R defined above is, indeed, an equivalence relation.
The reflexivity and symmetry of R are obvious.
Assume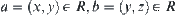 
, i.e., there exist 
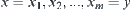such that 
, 
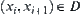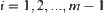, and 
,
.
, i.e., there exist such that , , and 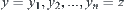,.Let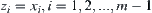 
,
.
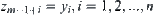,.We have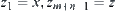 
, and 
.
, and 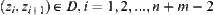.Consequently,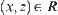 
, i.e., R has transitivity.
, i.e., R has transitivity.R is an equivalence relation.
Example 2.13
Assume that X is a network. B is a set of edges. R is an equivalence relation with B as its base. The quotient space corresponding to R is a space with connected components of X as its elements.
Next, we discuss below that in what conditions a normalized distance can produce a corresponding fuzzy equivalence relation.
Definition 2.18
For a normalized metric space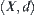 
, i.e., 
, 
, if any triangle composed by any non-collinear three points on X is an isosceles triangle, and its congruent legs are the longest side of the triangle, the distance in the space is called the isosceles distance.
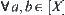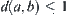, i.e., , , if any triangle composed by any non-collinear three points on X is an isosceles triangle, and its congruent legs are the longest side of the triangle, the distance in the space is called the isosceles distance.Proposition 2.12
is a normalized distance function on [X], the quotient space of X. Assume that
is an equivalence relation with 
as its base. Let 
. Then 
define a fuzzy equivalence relation 
on X uniquely, and with 
as its cut relation.Proof:
Let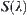 
be a quotient space corresponding to 
. From the definition of 
, we have 
, 
is a quotient space of 
. Thus, 
forms an ordered chain, under the inclusion relation of quotient spaces.
be a quotient space corresponding to 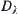. From the definition of 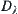, we have 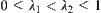, 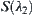is a quotient space of 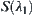. Thus, 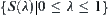forms an ordered chain, under the inclusion relation of quotient spaces.Then,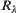 
satisfies that 
, 
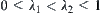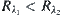. Therefore, 
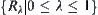defines a fuzzy equivalence relation 
on X uniquely, and with 
as its cut relation.
satisfies that , . Therefore, defines a fuzzy equivalence relation on X uniquely, and with 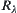as its cut relation.Proposition 2.13
If d is a normalized distance corresponding to a fuzzy equivalence relation, then it is an isosceles distance.
Proof:
Reduction to absurdity, otherwise, assume that there exist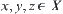 
such that 
. Thus,
does not satisfy the condition (3) in the definition of fuzzy equivalence relation.
such that 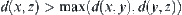. Thus,
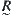does not satisfy the condition (3) in the definition of fuzzy equivalence relation.Theorem 2.4
is a quotient space of X. 
is a normalized isosceles distance function on [X]. By letting 
, then 
is a fuzzy equivalence relation on X.Proof:
Obviously,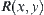 
satisfies the conditions (1) and (2) in the definition of fuzzy equivalence relation. We show that it also satisfies the condition (3).
satisfies the conditions (1) and (2) in the definition of fuzzy equivalence relation. We show that it also satisfies the condition (3).
, from d is an isosceles distance, 
. Thus, 
, i.e., 
.Carrying out the operation sup over y in the right hand side of the above formula, we have that 
satisfies condition (3) in the definition of fuzzy equivalence relation.
satisfies condition (3) in the definition of fuzzy equivalence relation.From Theorems 2.3 and 2.4, it’s known that a fuzzy equivalence relation on X is one-to-one correspondent to a normalized isosceles distance function on some [X]. The relationship shows that it is possible to use metric space as a tool for investigating fuzzy equivalence relations, or we can carry out study of fuzzy equivalence relations under the quotient space theoretical framework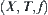 
, where T is a topology induced from a fuzzy equivalence relation.
, where T is a topology induced from a fuzzy equivalence relation.Moreover, from Proposition 2.12, it is known that a normalized distance d may produce a fuzzy equivalence relation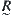 
on X. Theorem 2.3 and Proposition 2.13 show that 
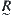can also produce a normalized isosceles distance 
. But 
generally, since d is not necessarily an isosceles distance. Turning d into 
is equivalent to changing a relation with only reflexive and symmetric properties to an equivalence relation, by a transitive operation.
on X. Theorem 2.3 and Proposition 2.13 show that can also produce a normalized isosceles distance . But 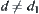generally, since d is not necessarily an isosceles distance. Turning d into 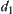is equivalent to changing a relation with only reflexive and symmetric properties to an equivalence relation, by a transitive operation.It has been proved that a fuzzy equivalence relation on X corresponds to a unique hierarchical structure of X. Conversely, their relation is also true, as we will show in the following theorem.
Theorem 2.5
Assuming that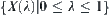 
is a hierarchical structure of X, there exists a fuzzy equivalence relation 
on X with cut relation 
, and 
is the quotient space corresponding to 
.
is a hierarchical structure of X, there exists a fuzzy equivalence relation on X with cut relation 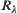, and 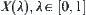is the quotient space corresponding to .Proof:
From the above assumption, 
is a hierarchical structure of X, and each 
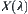is a quotient space of X. Let 
be an equivalence relation corresponding to 
. 
, define
is a hierarchical structure of X, and each is a quotient space of X. Let be an equivalence relation corresponding to 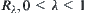. 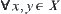, define
Letting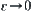 
, carrying out the sup operation over y in the right hand side of the above formula, we have 
.
, carrying out the sup operation over y in the right hand side of the above formula, we have 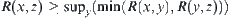.Finally,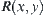 
is a fuzzy equivalence relation on X with 
as its cut relation.
is a fuzzy equivalence relation on X with 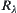as its cut relation.All the above results that we have can be summarized in the following basic theorem.
Basic Theorem
The following three statements are equivalent.
(1) A fuzzy equivalence relation on X;
(2) A normalized isosceles distance on some [X];
(3) A hierarchical structure of X.
Through the theorem, it follows that a fuzzy granular computing can be transformed into a computing on structure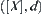 
. Therefore, quotient space theory is also available in fuzzy case.
. Therefore, quotient space theory is also available in fuzzy case.Example 2.14
A hierarchical structure of X is as follows.
Find their corresponding fuzzy equivalence relations.
Solution:
Let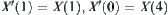 
.
.For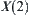 
, let 
.
, let 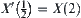.For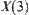 
, since 
, letting
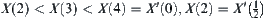, since , letting
Then, distance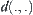 
as follows.
as follows.The distances between 6 and 13, 2 and 5, 14 and 16, 9 and 12, 3 and 11, 10 and 15 are 0, respectively.
The distances between 1 and 13 (or 6), 7 and 2 (or 5), 4 and 9 (or 12) are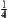 
, respectively.
, respectively.The distances between 8 and 1 (6 or 13), 14 (or 16) and 2 (5 or 7), 10 (or 15) and 4 (9 or 12) are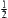 
, respectively.
, respectively.The distances between the other two elements are 1.
Letting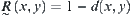 
, fuzzy equivalence relation 
corresponding to 
is the result that we want.
, fuzzy equivalence relation corresponding to 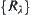is the result that we want.From the basic theorem and the above example, it is known that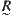 
corresponding to a hierarchical structure 
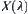of X is not unique. In other words, quotient space 
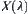based on cut relation 
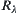that corresponding to 
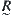represents the essence of 
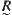. In fuzzy mathematics, this is called clustering structure 
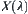of fuzzy equivalence relations. This means that if two fuzzy equivalence relations 
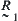and 
have the same clustering structure 
, then they are the same in essence. Their difference is superficial. So a hierarchical structure representation of X is more efficient than a fuzzy equivalence representation on X.
corresponding to a hierarchical structure of X is not unique. In other words, quotient space based on cut relation that corresponding to represents the essence of . In fuzzy mathematics, this is called clustering structure of fuzzy equivalence relations. This means that if two fuzzy equivalence relations and 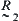have the same clustering structure 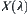, then they are the same in essence. Their difference is superficial. So a hierarchical structure representation of X is more efficient than a fuzzy equivalence representation on X.2.4.2. The Structure of Fuzzy Quotient Spaces
The Structure of Fuzzy Quotient Spaces
Definition 2.19
Assume that R is a fuzzy equivalence relation on X. From the basic theorem, there is a normalized isosceles distance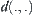 
on quotient space [X] of X corresponding to R. For 
, define 
. Thus, each 
defines a fuzzy set on [X]. The space composed by these fuzzy sets corresponds to fuzzy quotient space 
of fuzzy equivalence relation R. These fuzzy sets compose a fuzzy knowledge base.
on quotient space [X] of X corresponding to R. For 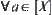, define 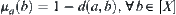. Thus, each 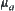defines a fuzzy set on [X]. The space composed by these fuzzy sets corresponds to fuzzy quotient space 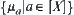of fuzzy equivalence relation R. These fuzzy sets compose a fuzzy knowledge base.Definition 2.20
Assume that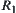 
and 
are two fuzzy equivalence relations. If for 
, there exists 
, then 
is called finer than 
, and denoted by 
.
and are two fuzzy equivalence relations. If for 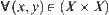, there exists 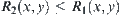, then 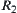is called finer than 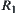, and denoted by 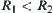.Theorem 2.6
Under the ‘<’ relation defined in Definition 2.20, the whole fuzzy quotient spaces on X compose a semi-order lattice.
Proof:
Given a set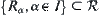 
, define 
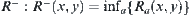and 
, satisfy 
, define and 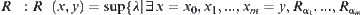, satisfy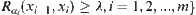 We show below that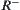 
is the supremum of 
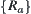. First, we show that it is a fuzzy equivalence relation.
is the supremum of . First, we show that it is a fuzzy equivalence relation.The reflexivity and symmetry of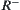 
are obvious. Now, we show its transitivity.
are obvious. Now, we show its transitivity.Assume that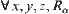 
, 
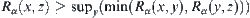. From the definition of operation ‘inf’, we have
, . From the definition of operation ‘inf’, we have
Carrying out the operation ‘inf’ in regard to 
over the left hand side of the above formula, we have 
. Then, R– is a fuzzy equivalence relation.
over the left hand side of the above formula, we have 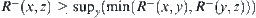. Then, R– is a fuzzy equivalence relation.Now, assume that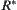 
is an upper bound of 
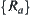, i.e., 
, 
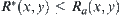. Carrying out the operation ‘inf’ in regard to 
over the right hand side of the above formula, we have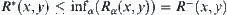 
. Thus, 
is the supremum of 
.
is an upper bound of , i.e., , . Carrying out the operation ‘inf’ in regard to over the right hand side of the above formula, we have . Thus, is the supremum of 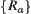.Now, we show that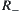 
is the infimum of 
. First, we show that it is a fuzzy equivalence relation.
is the infimum of . First, we show that it is a fuzzy equivalence relation.The reflexivity and symmetry of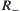 
are obvious. Now, we show its transitivity.
are obvious. Now, we show its transitivity.For any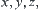 
assume 
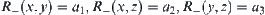. For 
, there exist 
such that 
, and there exist 
such that 
.
assume . For , there exist 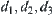such that 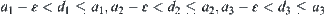, and there exist 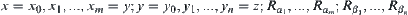such that 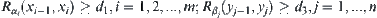.In assuming that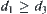 
, and letting 
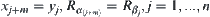, we have 
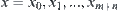and 
.
, and letting , we have and 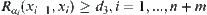.From the definition of 
, we have
, we have
Carrying out the operation ‘sup’ in regard to y over the right hand side of the above formula, and letting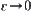 
, we then have 
. That is, 
satisfies the transitivity, and 
is a fuzzy equivalence relation.
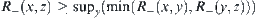, we then have . That is, 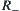satisfies the transitivity, and 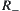is a fuzzy equivalence relation.Finally, we show that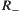 
is the infimum of 
.
is the infimum of 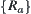.Assume that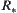 
is a lower bound of 
. For any 
, 
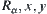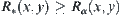. Assume 
. From the definition of 
, for any 
, there exist 
such that 
.
is a lower bound of . For any , . Assume . From the definition of 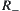, for any 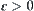, there exist 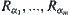such that 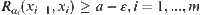.Construct a cut relation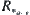 
. Since 
, x and y are equivalent under the cut relation 
, i.e., 
. Letting 
, we have 
. Thus, 
, i.e., 
is the infimum of 
.
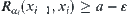. Since , x and y are equivalent under the cut relation 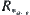, i.e., 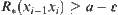. Letting 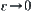, we have 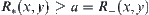. Thus, 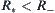, i.e., 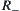is the infimum of 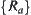.So far we have proved that via fuzzy equivalence relation, the common quotient space theory can be extended to the fuzzy issues. First, we show that the following four statements are equivalent: (1) a fuzzy equivalence relation R on X, (2) a normalized isosceles distance d on quotient space [X] of X, (3) a hierarchical structure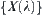 
of X, (4) a fuzzy knowledge base of X. Secondly, we show that the whole fuzzy equivalence relations on X compose a semi-order lattice. These results provide a powerful tool for quotient space based fuzzy granular computing.
of X, (4) a fuzzy knowledge base of X. Secondly, we show that the whole fuzzy equivalence relations on X compose a semi-order lattice. These results provide a powerful tool for quotient space based fuzzy granular computing.2.4.3. Cluster and Hierarchical Structure
In real problems, fuzzy equivalence relation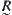 
can be used for cluster analysis. So a cluster analysis is equivalent to a hierarchical structure of X corresponding to 
.
can be used for cluster analysis. So a cluster analysis is equivalent to a hierarchical structure of X corresponding to 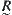.Since a fuzzy equivalence relation equals to a normalized isosceles distance on a quotient space of X, distance 
can be used for distance analysis, i.e., the quotient space method based on equivalence relation 
, 
as its base, can be used for cluster analysis. The method is the same as the ‘the maximal tree’ method of cluster analysis in fuzzy mathematics.
can be used for distance analysis, i.e., the quotient space method based on equivalence relation 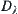, 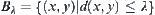as its base, can be used for cluster analysis. The method is the same as the ‘the maximal tree’ method of cluster analysis in fuzzy mathematics.Example 2.15
is a fuzzy similar relation on X, 
. 
is represented by a symmetric matrix as follows.| rii | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 1 | 1 | |||||||||||||
| 2 | 0 | 1 | ||||||||||||
| 3 | 0 | 0 | 1 | |||||||||||
| 4 | 0 | 0 | 0.4 | 1 | ||||||||||
| 5 | 0 | 0.8 | 0 | 0 | 1 | |||||||||
| 6 | 0.5 | 0 | 0.2 | 0.2 | 0 | 1 | ||||||||
| 7 | 0 | 0.8 | 0 | 0 | 0.4 | 0 | 1 | |||||||
| 8 | 0.4 | 0.2 | 0.2 | 0.4 | 0 | 0.8 | 0 | 1 | ||||||
| 9 | 0 | 0.4 | 0 | 0.8 | 0.4 | 0.2 | 0.4 | 0 | 1 | |||||
| 10 | 0 | 0 | 0.2 | 0.2 | 0 | 0 | 0.2 | 0 | 0.2 | 1 | ||||
| 11 | 0 | 0.5 | 0.2 | 0.2 | 0 | 0 | 0.8 | 0 | 0.4 | 0.2 | 1 | |||
| 12 | 0 | 0 | 0.2 | 0.8 | 0 | 0 | 0 | 0 | 0.4 | 0.8 | 0 | 1 | ||
| 13 | 0.8 | 0 | 0.2 | 0.4 | 0 | 0.4 | 0 | 0.4 | 0 | 0 | 0 | 0 | 1 | |
| 14 | 0 | 0.8 | 0 | 0.2 | 0.4 | 0 | 0.8 | 0 | 0.2 | 0.2 | 0.6 | 0 | 0 | 1 |
Letting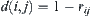 
, we construct a quotient space based on distance as follows.
, we construct a quotient space based on distance as follows.
We have X(1)<X(0.5)<X(0.2)<X(0) and X(1)=X(0.8)=X(0.6).
From metric spaces to survey quotient space 
, roughly speaking, the element of 
is regarded as a point that consists of all points which distance is
. Since a fuzzy equivalence relation is equivalent to a hierarchical structure, we can survey the fuzziness from the hierarchical point of view. For example, when using a ruler to measure lengths, if the minimal unit of the rule is ‘meter’, for an object with length 12 meters, then 12 meters is a certain concept, since it is neither 11 nor 13 meters. But in the finer level, ‘centimeter’ level, its length becomes about 1200 cm, then 1200 cm is an uncertain (fuzzy) concept, since it might be either 1201 or 1199 cm, etc. So the concepts between crisp and fuzzy are relative. Multi-granular computing can handle the relations between crisp and fuzzy, certain and uncertain efficiently. More details will be discussed in Section 2.5.
, roughly speaking, the element of is regarded as a point that consists of all points which distance is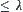. Since a fuzzy equivalence relation is equivalent to a hierarchical structure, we can survey the fuzziness from the hierarchical point of view. For example, when using a ruler to measure lengths, if the minimal unit of the rule is ‘meter’, for an object with length 12 meters, then 12 meters is a certain concept, since it is neither 11 nor 13 meters. But in the finer level, ‘centimeter’ level, its length becomes about 1200 cm, then 1200 cm is an uncertain (fuzzy) concept, since it might be either 1201 or 1199 cm, etc. So the concepts between crisp and fuzzy are relative. Multi-granular computing can handle the relations between crisp and fuzzy, certain and uncertain efficiently. More details will be discussed in Section 2.5.2.4.4. Conclusions
In order to extend quotient space theory to fuzzy spaces, there are three different ways. First, the fuzzification of domains, i.e., domain X is composed by fuzzy objects. Second, the fuzzification of structures, i.e., the structure is a fuzzy topology. Third, a fuzzy quotient space theory is established by expanding to fuzzy equivalent relations. In the section, we only discuss the third way. We have its basic property as follows. A fuzzy equivalence relation on X is equivalent to a normalized isosceles distance on some quotient space [X] and also equivalent to a unique hierarchical structure of X. These results closely integrate the quotient space theory with fuzzy mathematics.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.