3.2 Structural Equation Model

The hypothesized structural relations between latent variables are defined by a set of equations in a SEM model. Different from the path analysis, SEM focuses causal relationships among unobserved latent variables instead of among observed variables. Recall that a SEM model is a two-part model, consisting of the measurement model (CFA) and structural equations. In the measurement model part of the model, linear (e.g., when observed indicators are continuous measures) or nonlinear (e.g., when observed indicators are categorical measures) equations describe the relations between the observed variables and their underlying latent variables/factors; and in the structural equations part of the model, endogenous latent variables () are regressed on the exogenous latent variables () and/or some other endogenous latent variables. In addition, observed variables can also be included as either dependent and/or independent variables in a SEM model.

The measurement model part of the SEM model is described as:

(3.7)

where and are vectors of intercepts of regressing observed y and x indicators on endogenous latent variables and exogenous latent variables, respectively. The structural equations part of the model is described as:

(3.8)

Figure 3.3 shows a SEM model using variables selected from the BSI-18 data, in which depression (, DEP) and anxiety (, ANX) are two endogenous latent variables that are predicted by a set of socio-demographic variables, such as Gender (1, male; 0, female), Ethnic (1, white; 0, non-whites), Age, and Hsch (1, high school and above; 0, lower than high school). The relationship between depression and anxiety is complicated. The two constructs are different but not mutually exclusive. Medical findings show that the majority of the patients who have depression also have a condition of generalized anxiety disorder, and some forms of depression may originally start with anxiety. In this example model, we specify (DEP) as a function of (ANX) for the purpose of model demonstration. The model can be described in matrix notation as below:

Figure 3.3 Structural equation model.

(3.9)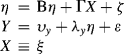

where the intercepts of latent variables in the structural equation part of the model are fixed to zero for model identification as this is a single group model; the intercepts of the endogenous indicators (i.e., the y variables) are free parameters; all the exogenous latent variables () are assumed to be measured perfectly by the observed exogenous indicators (i.e., the x variables) without measurement errors. The structural equations can be further described as:

(3.10)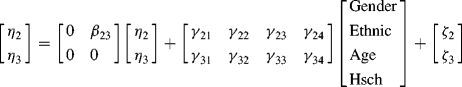

that is

(3.11)

The model is estimated by the following Mplus program.

Mplus Program 3.5

The model fits data very well: RMSEA = 0.050 (90% CI: 0.035, 0.064), close fit test is not statistically significant (P = 0.483), CFI = 0.951, TLI = 0.940, and SRMR = 0.041. The latent variable anxiety (ANX) has a significant positive effect (0.910, P < 0.001) on depression (DEP); socio-demographic covariates, such as gender, age, ethnicity, and education, have no significant effects on depression. However gender has a significant negative effect on anxiety (−0.511, P < 0.001); white people were likely to have severer anxiety than non-whites (0.484, P = 0.007). The percentage of explained variation in DEP is high (R² = 0.678), and the corresponding figure is R² = 0.111 for ANX (see the R-SQUARE section in Table 3.5).

Table 3.5 Selected Mplus output: structural equation model.

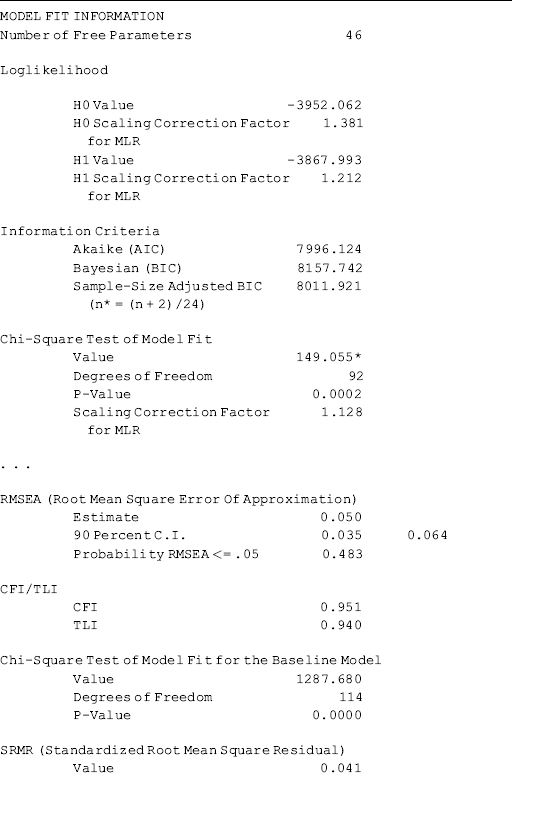
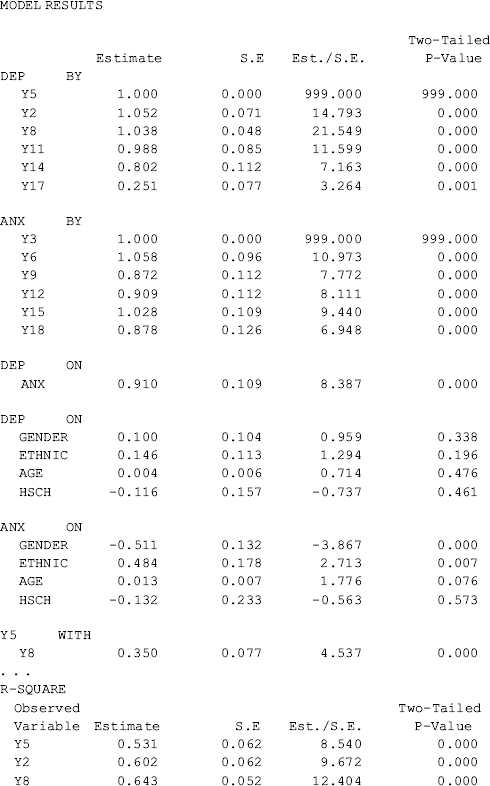
Although the means/intercepts of latent variables in the SEM model are fixed to zero for model identification, and no latent variable means/intercepts are reported in the MODEL RESULTS section of the Mplus output (Table 3.5), estimated ‘means’ for the latent variables are reported in the section of TECHNICAL 4 OUTPUT (Table 3.5). As explained in the section of MIMIC model results, these are in fact not estimated latent variable/factor means, but take information about the covariates into account. Once we remove the covariates from the model, these factor ‘means’ reported in TECHNICAL 4 OUTPUT will become zeros.

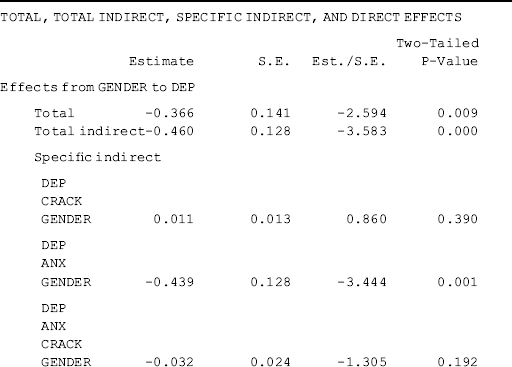
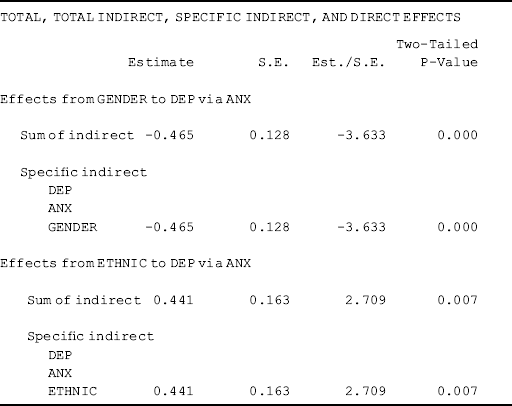
Testing indirect effects. The MODEL RESULTS from Table 3.5 imply that covariates Gender and Ethnic may indirectly affect depression via anxiety although none of them has a significant direct effect on depression. Testing indirect effects is an important feature in path analysis and SEM. The following Mplus program shows how to test the indirect effects of the covariates Gender and Ethnic on depression via anxiety.

Mplus Program 3.6

where the MODEL INDIRECT command is used to request estimates of indirect effects and their standard errors. The VIA option of the MODEL INDIRECT command is used to test the indirect effects of covariates Gender and Ethnic on DEP via ANX. That is, the effects of Gender and Ethnic on DEP are mediated by ANX.

Table 3.6 shows that Gender has a negative (−0.465, P < 0.001), while Ethnic has a positive (0.441, P = 0.007), indirect effect on DEP via ANX. Both Gender and Ethnic have only one indirect effect in this example.

Table 3.6 Selected Mplus output: testing indirect effects.

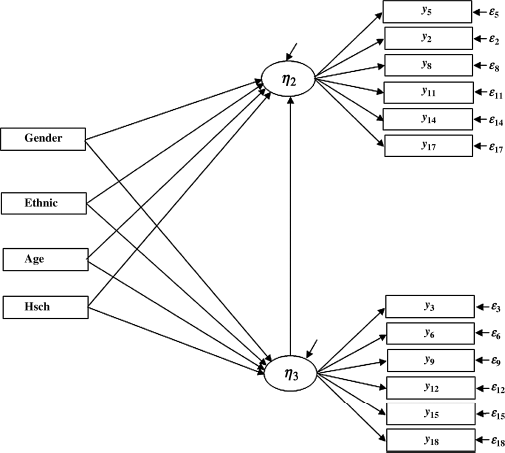
In a more sophisticated model, an exogenous (either observed or latent) variable or endogenous (either observed or latent) variable may indirectly affect other endogenous (either observed or latent) variables. Its specific indirect and total effects on an endogenous variable can be tested. In Figure 3.4, an additional endogenous variable (i.e., Crack measuring crack-cocaine use frequency in the past 30 days) is included in the model. This variable is an observed endogenous variable assuming no measurement error at the moment. Again, the relationship between substance abuse and mental health is complicated. Given the links between substance abuse and mental problems, the connections may arise from several different mechanisms. Substance abuse may potentially trigger or relate to the development of psychiatric symptoms. Conversely, underlying psychopathology may contribute to the abuse of psychoactive substances.

Figure 3.4 Testing indirect and total effects in SEM.

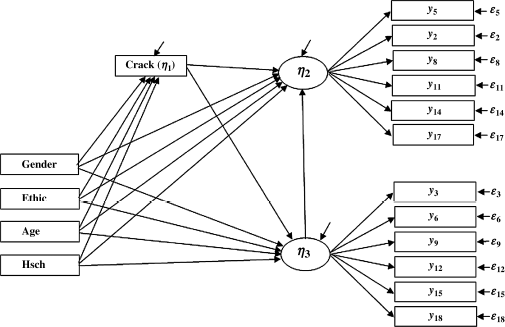
In addition, some factors may increase individuals' vulnerability to both substance abuse and mental illness. For the purpose of model demonstration, we assume crack-cocaine use causes mental problems, and there is no reciprocal effect in our example model.³ Covariates (e.g., Gender, Ethnic, Age, and Hsch), which are observed exogenous variables, are hypothesized to influence the endogenous latent variables anxiety (, ANX) and depression (, DEP), as well as the exogenous observed variable crack-cocaine frequency (, Crack). We will test the direct effect, indirect effect, and the total effect of Gender and Ethnic on DEP in the following Mplus program.

Mplus Program 3.7

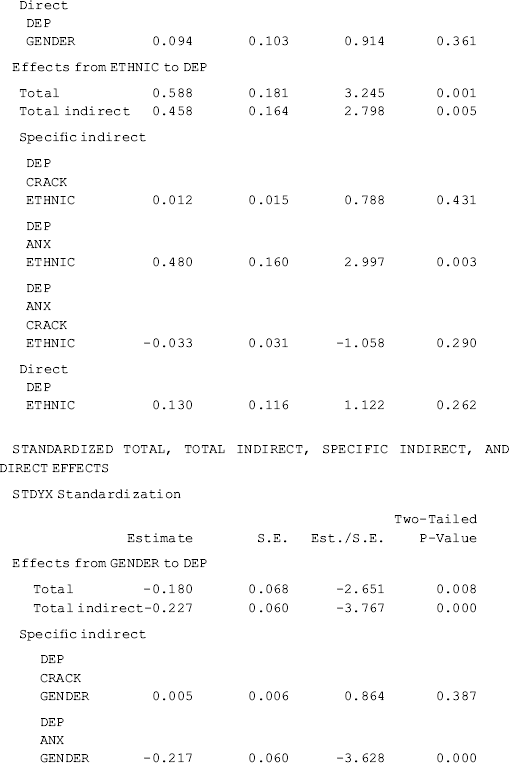
where IND option in the MODEL INDIRECT command is used to test the specific indirect effects, total indirect effects, and total effects. The variable on the left-hand side of IND statement is the dependent variable, and the variable on the right-hand side is the independent variable. If a mediating variable is specified between IND and the independent variable, the program will produce only specific indirect and total indirect effects of the independent variable via the mediating variable. In the above example, no mediating variables are specified, thus the DEP IND Gender statement requests estimates of the direct effect, specific indirect effects, total specific effect, and the total effect of Gender on DEP.

The direct effect of Gender on DEP is not statistically significant (0.094, P = 0.361), but its total indirect effect is negative and statistically significant (−0.460, P < 0.001), which consists of three specific indirect effects: (1) specific indirect effect via Crack (0.011, P = 0.390); (2) via ANX (−0.439, P = 0.001); and (3) via Crack and then via ANX (−0.032, P = 0.192). The total effect of Gender on DEP, which is the sum of all its direct and indirect effects, is statistically significant (−0.366, P = 0.009). The effects of Ethnic on DEP are interpreted in the same way.

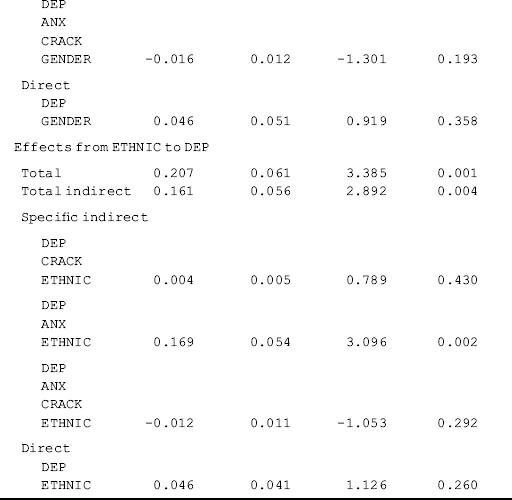
The standardized direct, indirect, and total effects are shown in Table 3.7. Slope coefficients based on standardized solution can be compared with each other. For example, the specific indirect effect of Gender on DEP via ANX is −0.217 (P < 0.00), while the corresponding indirect effect of Ethnic is 0.169 (P = 0.002). Thus, we may conclude that Gender has larger indirect effect on DEP via ANX than Ethnic does although such indirect effects of the two covariates go in opposite directions.

Table 3.7 Selected Mplus output: testing direct, specific indirect, total indirect and total effects.