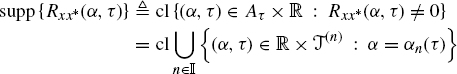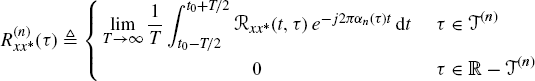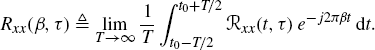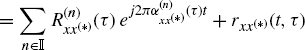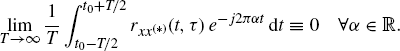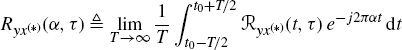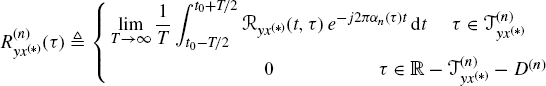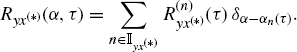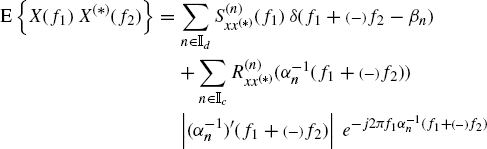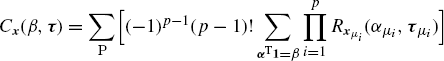2.2 Characterization of GACS Stochastic Processes
In this section, the strict-sense, second-order wide-sense, and higher-order characterizations of GACS stochastic processes are presented in the time domain. Moreover, the second-order spectral characterization is discussed. Examples of GACS processes and motivations to adopt such a model are provided. See (Izzo and Napolitano 1998a) and (Izzo and Napolitano 2002a) for a treatment in the nonstochastic or functional approach.
2.2.1 Strict-Sense Statistical Characterization
Definition 2.2.1 The real-valued process ![]() , is said to be with almost-periodic structure in the strict sense if its Nth-order distribution function
, is said to be with almost-periodic structure in the strict sense if its Nth-order distribution function
(2.1) ![]()
is almost-periodic in t (in one of the senses considered in Section 1.2), for every fixed ![]() .
.
Thus, for a process with almost-periodic structure in the strict sense, the Nth-order distribution function can be expressed by the (generalized) Fourier series
(2.2) ![]()
where ![]() is a countable set depending on
is a countable set depending on ![]() and
and ![]() and
and
(2.3) 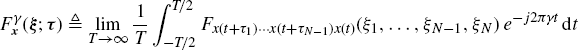
Definition 2.2.2 The real-valued process ![]() , is said to be Nth-order generalized almost-cyclostationary in the strict sense if for every
, is said to be Nth-order generalized almost-cyclostationary in the strict sense if for every ![]() the set
the set
is countable (see (Izzo and Napolitano 2005) for the definition in the functional (or nonstochastic) approach).
Definition 2.2.3 The real-valued process ![]() , is said to be Nth-order almost-cyclostationary in the strict sense if the set
, is said to be Nth-order almost-cyclostationary in the strict sense if the set
(2.5) ![]()
is countable.
Theorem 2.2.4 For a Nth-order generalized almost-cyclostationary process (![]() countable and
countable and ![]() uncountable) the result is that
uncountable) the result is that
(2.6b) ![]()
with ![]() countable and
countable and
(2.7) ![]()
where ![]() denotes Kronecker delta, that is,
denotes Kronecker delta, that is, ![]() for
for ![]() and
and ![]() .
.
Proof: It is similar to the proof of Theorem 2.2.7.
Theorem 2.2.5 An Nth-order GACS process in the strict sense has the Nth-order temporal moment function which is an almost-periodic function of t with frequencies depending on ![]() .
.
Proof: Accounting for (2.6a), the result is that
(2.8) 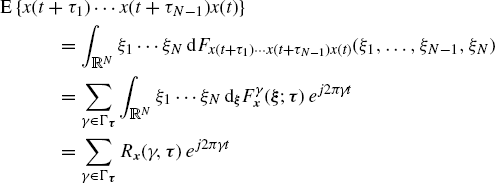
where
(2.9) 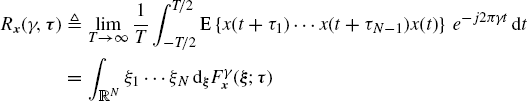
are the cyclic temporal moment functions.
Note that a similar result cannot be derived in the more general case of process with almost-periodic structure in the strict sense, that is, with the set ![]() depending on both
depending on both ![]() and
and ![]() and such that the set
and such that the set ![]() defined in (2.4) is not countable. Digital signals
defined in (2.4) is not countable. Digital signals ![]() with values in a finite or countable set have
with values in a finite or countable set have ![]() countable.
countable.
2.2.2 Second-Order Wide-Sense Statistical Characterization
In this section, the second-order statistical characterization in the wide sense of GACS signals is provided. Emphasis is given to second-order (cross-) moment properties, while no emphasis is given to mean value properties.
Definition 2.2.6 A finite-power complex-valued continuous-time stochastic process ![]() is said to be second-order GACS in the wide sense if its mean value is an almost-periodic function and its autocorrelation function
is said to be second-order GACS in the wide sense if its mean value is an almost-periodic function and its autocorrelation function
with ![]() denoting statistical expectation, for each
denoting statistical expectation, for each ![]() is almost-periodic in t in the sense of Bohr (Bohr 1933, paragraphs 84–92) or, equivalently, uniformly almost periodic in sense of Besicovitch (Besicovitch 1932, Chapter 1), (Corduneanu 1989). That is, for each fixed
is almost-periodic in t in the sense of Bohr (Bohr 1933, paragraphs 84–92) or, equivalently, uniformly almost periodic in sense of Besicovitch (Besicovitch 1932, Chapter 1), (Corduneanu 1989). That is, for each fixed ![]()
![]() is the limit of a uniformly convergent sequence of trigonometric polynomials in t
is the limit of a uniformly convergent sequence of trigonometric polynomials in t
In (2.11), the real numbers α and the complex-valued functions ![]() referred to as cycle frequencies and cyclic autocorrelation functions, are the frequencies and coefficients, respectively, of the (generalized) Fourier series expansion of
referred to as cycle frequencies and cyclic autocorrelation functions, are the frequencies and coefficients, respectively, of the (generalized) Fourier series expansion of ![]() that is,
that is,
with the limit independent of ![]() . Moreover,
. Moreover,
is a countable set (of possibly incommensurate cycle frequencies) which, in general, depends on τ.
Note that, even if the set Aτ is countable, the set
is not necessarily countable. Thus, the class of the second-order wide-sense GACS processes extends that of the wide-sense ACS which are obtained as a special case of GACS processes when the set A is countable (Dehay and Hurd 1994), (Hanin and Schreiber 1998), (Hurd 1991).
A useful characterization of wide-sense GACS processes can be obtained by observing that the set Aτ can be expressed as
where ![]() is a countable set and the functions
is a countable set and the functions ![]() , referred to as lag-dependent cycle frequencies and in the following denoted by
, referred to as lag-dependent cycle frequencies and in the following denoted by ![]() for notation simplicity when this does not create ambiguity, are such that, for each α and τ, there exists at most one
for notation simplicity when this does not create ambiguity, are such that, for each α and τ, there exists at most one ![]() such that
such that ![]() . Thus, accounting for the countability of
. Thus, accounting for the countability of ![]() for each τ, the support in the
for each τ, the support in the ![]() -plane of the cyclic autocorrelation function
-plane of the cyclic autocorrelation function ![]() is constituted by the closure of the set of curves defined by the explicit equations
is constituted by the closure of the set of curves defined by the explicit equations ![]() :
:
where
The closure of a countable set of curves can be the whole plane ![]() if infinities of clusters of curves exist. In such a case, the more appropriate concept of “being concentrated on” (Dehay 1994) can be used to describe the region of the
if infinities of clusters of curves exist. In such a case, the more appropriate concept of “being concentrated on” (Dehay 1994) can be used to describe the region of the ![]() -plane where
-plane where ![]() .
.
Starting from (2.16), the following result (Izzo and Napolitano 1998a, 2002a) provides an alternative representation for the autocorrelation function of GACS processes.
Theorem 2.2.7 The autocorrelation function ![]() of a second-order wide-sense GACS process can be expressed as
of a second-order wide-sense GACS process can be expressed as
where the functions ![]() referred to as generalized cyclic autocorrelation functions, are defined as
referred to as generalized cyclic autocorrelation functions, are defined as
with the limit in (2.19) independent of ![]() .
.
Note that, in (2.18) the sum ranges over a set not depending on τ as, on the contrary, it occurs in (2.11). Moreover, unlike the case of second-order ACS processes, both coefficients and frequencies of the Fourier series in (2.18) depend on the lag parameter τ.
Fact 2.2.8 The functions ![]() in (2.15)–(2.17) are such that, for each
in (2.15)–(2.17) are such that, for each ![]() for
for ![]() . However, if more functions
. However, if more functions ![]() are defined in K (not necessarily coincident) neighborhoods of the same point
are defined in K (not necessarily coincident) neighborhoods of the same point ![]() , all have the same limit, say
, all have the same limit, say ![]() , for
, for ![]() , and only one of them is defined in
, and only one of them is defined in ![]() , then it is convenient to assume all the functions
, then it is convenient to assume all the functions ![]() defined in
defined in ![]() with
with ![]() and, consequently, define
and, consequently, define
where, for each i, the limit is made with τ ranging in ![]() . With convention (2.20), by taking the coefficient of the complex sinewave at frequency α (see (2.12)) in both sides of (2.18), it follows that the cyclic autocorrelation function and the generalized cyclic autocorrelation functions are related by the relationship
. With convention (2.20), by taking the coefficient of the complex sinewave at frequency α (see (2.12)) in both sides of (2.18), it follows that the cyclic autocorrelation function and the generalized cyclic autocorrelation functions are related by the relationship
where ![]() denotes Kronecker delta, that is,
denotes Kronecker delta, that is, ![]() .
.
The wide-sense ACS processes are obtained as a special case of GACS processes when the lag-dependent cycle frequencies are constant with respect to τ and, hence, are coincident with the cycle frequencies (Izzo and Napolitano 1998a). In such a case,
(2.22) ![]()
(2.24) ![]()
Moreover, for ACS processes only one term is present in the sum in (2.21) and, consequently, the generalized cyclic autocorrelation functions are coincident with the cyclic autocorrelation functions. Furthermore, the autocorrelation function ![]() depends uniformly on the parameter τ (Corduneanu 1989, Chapter 2) and is uniformly continuous and the cyclic autocorrelation functions
depends uniformly on the parameter τ (Corduneanu 1989, Chapter 2) and is uniformly continuous and the cyclic autocorrelation functions ![]() are continuous in τ for each
are continuous in τ for each ![]() (which is countable) (Hurd 1991), (Dehay and Hurd 1994).
(which is countable) (Hurd 1991), (Dehay and Hurd 1994).
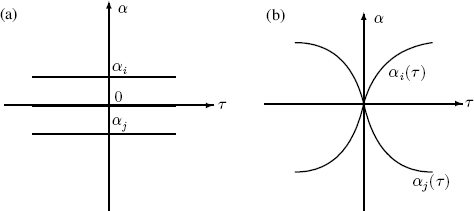
In Figure 2.1, the support in the ![]() plane of the cyclic autocorrelation function
plane of the cyclic autocorrelation function ![]() is reported for (a) an ACS signal and (b) a GACS (not ACS) signal. For the ACS signal, such a support is contained in the lines
is reported for (a) an ACS signal and (b) a GACS (not ACS) signal. For the ACS signal, such a support is contained in the lines ![]() , that is, lines parallel to the τ axis corresponding to the cycle frequencies (see (2.23)). For the GACS signal, the support is constituted by the curves
, that is, lines parallel to the τ axis corresponding to the cycle frequencies (see (2.23)). For the GACS signal, the support is constituted by the curves ![]() (see (2.16)).
(see (2.16)).
Figure 2.1 Support in the (α, τ)-plane of the cyclic autocorrelation function ![]() of (a) an ACS process and (b) a GACS (not ACS) process
of (a) an ACS process and (b) a GACS (not ACS) process
Lemma 2.2.9 Second-order GACS processes in the wide sense have uniformly bounded second-order absolute moments.
Proof: For every τ the autocorrelation function ![]() is uniformly almost-periodic with respect to the variable t. Therefore, such a function is bounded and its (generalized) Fourier series is uniformly convergent (Definition 2.2.6). Thus, from
is uniformly almost-periodic with respect to the variable t. Therefore, such a function is bounded and its (generalized) Fourier series is uniformly convergent (Definition 2.2.6). Thus, from ![]() it follows that GACS processes have uniformly bounded second-order absolute moments (see (Dehay and Hurd 1994) for the case of ACS processes).
it follows that GACS processes have uniformly bounded second-order absolute moments (see (Dehay and Hurd 1994) for the case of ACS processes).
For complex processes, two second-order moments need to be considered for a complete characterization in the wide sense: the autocorrelation function (2.10) and the conjugate autocorrelation function (Gardner 1987d) also called relation function (Picinbono and Bondon 1997) or complementary correlation (Schreier and Scharf 2003a)
(2.25) ![]()
For complex-valued GACS processes, similar representations must hold for the autocorrelation and the conjugate autocorrelation functions and Definition 2.2.6, Theorem 2.2.7, and Fact 2.2.8 must be extended to ![]() . That is,
. That is, ![]() is the uniform limit of a sequence of trigonometric polynomials whose coefficients
is the uniform limit of a sequence of trigonometric polynomials whose coefficients ![]() and frequencies
and frequencies ![]() are referred to as conjugate generalized cyclic autocorrelation functions and conjugate lag-dependent cycle frequencies, respectively. The conjugate cyclic autocorrelation function at conjugate cycle frequency β is
are referred to as conjugate generalized cyclic autocorrelation functions and conjugate lag-dependent cycle frequencies, respectively. The conjugate cyclic autocorrelation function at conjugate cycle frequency β is
The cyclic autocorrelation function (2.12) and the conjugate cyclic autocorrelation function (2.26) can both be represented by the concise notation
(2.27) 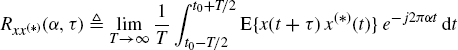
where superscript (*) represents an optional complex conjugation.
More general definitions of GACS processes can be given if the almost-periodicity property is considered in one of the generalized senses presented in Sections 1.2.2, 1.2.3, 1.2.4, and 1.2.5. In particular, a stochastic process ![]() is said to exhibit (conjugate) second-order cyclostationarity in the wide sense with (conjugate) cycle frequency α if the (conjugate) cyclic autocorrelation function
is said to exhibit (conjugate) second-order cyclostationarity in the wide sense with (conjugate) cycle frequency α if the (conjugate) cyclic autocorrelation function ![]() is nonzero for some τ. Its (conjugate) autocorrelation function has the form
is nonzero for some τ. Its (conjugate) autocorrelation function has the form
with ![]() and
and ![]() countable sets depending on (*), and
countable sets depending on (*), and ![]() residual term not containing any finite-strength additive sinewave component
residual term not containing any finite-strength additive sinewave component
For each fixed τ, the function ![]() in (2.28b) is a generalized almost-periodic function of t in the sense of Hartman and Ryll-Nardzewski (Section 1.2.5). More generally, the function
in (2.28b) is a generalized almost-periodic function of t in the sense of Hartman and Ryll-Nardzewski (Section 1.2.5). More generally, the function
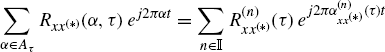
is not necessarily continuous in t and τ.
If condition (2.29) is assured by the asymptotic vanishing of the residual term
(2.30) ![]()
and, in addition, the lag-dependent cycle frequencies do not depend on τ, then the stochastic process x(t) is called asymptotically almost cyclostationary (Gardner 1978).
Definition 2.2.10 Two finite-power complex-valued continuous-time stochastic process ![]() and
and ![]() are said to be jointly GACS in the wide sense if
are said to be jointly GACS in the wide sense if
In (2.31b) and (2.31c), ![]() are countable sets and the lag-dependent cycle frequencies
are countable sets and the lag-dependent cycle frequencies ![]() depend on the choice made for the optional complex conjugation (*) and, in general, are not coincident with those of
depend on the choice made for the optional complex conjugation (*) and, in general, are not coincident with those of ![]() or
or ![]() . The result is that
. The result is that
(2.32b) 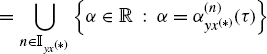
(2.32c) ![]()
The function
is the cyclic cross-correlation function and the functions ![]() are the generalized cyclic cross-correlation functions defined as
are the generalized cyclic cross-correlation functions defined as
where
(2.36) ![]()
(2.37) ![]()
and the limit in (2.35) is made with τ ranging in ![]() .
.
Moreover, from (2.34) for ![]() one obtains
one obtains
(2.8) ![]()
and by reasoning as for a single process, it can be shown that for every τ
For GACS processes that are not ACS, even if the set Aτ defined in (2.15) and the (conjugate) autocorrelation function ![]() are continuous functions of the lag parameter τ, the (conjugate) cyclic autocorrelation function
are continuous functions of the lag parameter τ, the (conjugate) cyclic autocorrelation function ![]() is not a continuous function of τ. Specifically, according to (2.39) with
is not a continuous function of τ. Specifically, according to (2.39) with ![]() is constituted by sums of Kronecker deltas depending on τ.
is constituted by sums of Kronecker deltas depending on τ.
It is well known that for every finite-power process x(t) the conventional time-averaged autocorrelation function ![]() is continuous in τ = 0 (and, hence, for any τ) if and only if the cross-correlation function
is continuous in τ = 0 (and, hence, for any τ) if and only if the cross-correlation function ![]() is continuous for any
is continuous for any ![]() and for any finite-power process y(t) (Lee 1967, pp. 74–78). Therefore, if one defines the process
and for any finite-power process y(t) (Lee 1967, pp. 74–78). Therefore, if one defines the process
(2.40) ![]()
then the (conjugate) cyclic autocorrelation function of x(t) can be written as
(2.41) ![]()
Consequently, the time-averaged autocorrelation function ![]() is continuous in
is continuous in ![]() if and only if the (conjugate) cyclic autocorrelation function is continuous in
if and only if the (conjugate) cyclic autocorrelation function is continuous in ![]() . Furthermore, such a property is still valid with reference to the continuity of all higher-order cyclic temporal moment functions (Izzo and Napolitano 1998a, 2005). Therefore, all GACS processes that are not ACS exhibit time-averaged autocorrelation functions discontinuous in
. Furthermore, such a property is still valid with reference to the continuity of all higher-order cyclic temporal moment functions (Izzo and Napolitano 1998a, 2005). Therefore, all GACS processes that are not ACS exhibit time-averaged autocorrelation functions discontinuous in ![]() . In particular, accounting for the symmetry property
. In particular, accounting for the symmetry property ![]() , it follows that
, it follows that ![]() contains the additive term
contains the additive term ![]() , where
, where ![]() is the time-averaged power of x(t). Consequently, as shown in Section 2.2.3, the power
is the time-averaged power of x(t). Consequently, as shown in Section 2.2.3, the power ![]() (or quota of it) is uniformly spread over an infinite bandwidth and this constitutes a strong difficulty for the spectral characterization of GACS processes. Note that the above-discussed discontinuity property should not be confused with that examined in (Hurd 1974), where the discontinuity of the time-varying autocorrelation function is considered.
(or quota of it) is uniformly spread over an infinite bandwidth and this constitutes a strong difficulty for the spectral characterization of GACS processes. Note that the above-discussed discontinuity property should not be confused with that examined in (Hurd 1974), where the discontinuity of the time-varying autocorrelation function is considered.
Definition 2.2.11 Mean-Square Continuity. The stochastic process ![]() is said to be mean-square continuous in t if
is said to be mean-square continuous in t if
(2.42) ![]()
Theorem 2.2.12 Necessary and Sufficient Condition for Mean-Square Continuity (Loève (1963), pp. 469–470). The stochastic process ![]() is mean-square continuous in t if and only if
is mean-square continuous in t if and only if
whatever way ![]() and
and ![]() converge to zero. That is, if and only if
converge to zero. That is, if and only if ![]() is continuous at
is continuous at ![]() .
.
From (2.43) it also follows that
(2.44) ![]()
Thus, as an immediate consequence of Theorem 2.2.12, we have that if ![]() is continuous at every diagonal point (t1, t1), then it is continuous for every (t1, t2).
is continuous at every diagonal point (t1, t1), then it is continuous for every (t1, t2).
Theorem 2.2.13 Non Mean-Square Continuity of GACS Processes. GACS processes which are not ACS are not mean-square continuous.
Proof: From Theorem 2.2.7 it follows that (see (2.18))
(2.45) ![]()
The lack of mean-square continuity of GACS processes which are not ACS follows immediately from the fact that for the lag-dependent cycle frequency ![]() we have
we have ![]() discontinuous in
discontinuous in ![]() . Therefore, the necessary condition of Theorem 2.2.12 is not satisfied.
. Therefore, the necessary condition of Theorem 2.2.12 is not satisfied.
In contrast, ACS processes are mean-square continuous and are characterized by the following conditions (Hurd 1991), (Gardner et al. 2006):
Definition 2.2.14 Mean-Square Integrability. The stochastic process ![]() is said to be (Riemann) mean-square integrable in
is said to be (Riemann) mean-square integrable in ![]() if
if
where ![]() , with
, with ![]() being the integer part.
being the integer part.
Theorem 2.2.15 Necessary and Sufficient Condition for Mean-Square Integrability (Loève 1963, p. 472). The zero-mean stochastic process ![]() is mean-square integrable in
is mean-square integrable in ![]() if and only if
if and only if
Assumption 2.2.16 Cesàro Summability of the Autocorrelation Function. For every finite T it results that
Since for ![]() it results
it results ![]() , a sufficient condition assuring that (2.48) holds is
, a sufficient condition assuring that (2.48) holds is
(2.49) 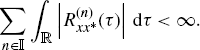
Theorem 2.2.17 Mean-Square Integrability of GACS Processes. Under Assumption 2.2.16, a GACS process is mean-square integrable in ![]() .
.
Proof: See Section 3.1.
In (Napolitano 2003) the class of the spectrally correlated (SC) processes is introduced, which is a further class that generalizes that of the ACS processes. SC processes have a Loève bifrequency spectrum (Loève (1963), Chapter X) with spectral masses concentrated on a countable set of curves in the bifrequency plane (Chapter 4). Thus, ACS processes are obtained as special case of SC processes when the support curves are lines with unit slope (Hurd 1989a, 1991), (Dehay and Hurd 1994). Specifically, SC processes exhibit spectral correlation between spectral components that are separated, and the separation between correlated spectral components depends on the shape of the support curves in the bifrequency plane. For ACS processes, correlation exists only between spectral components that are separated by quantities belonging to a countable set of values, the cycle frequencies, which are the frequencies of the (generalized) Fourier series expansion of the autocorrelation function which is an almost-periodic function of time. Therefore, ACS processes are obtained by the intersection of the class of the GACS processes and the class of the SC processes. That is, ACS processes are a subclass of GACS processes that exhibit the spectral correlation property (Napolitano 2007b) (Section 4.2.2).
Let ![]() be the set
be the set
where ![]() in (2.50) are the lag-dependent cycle frequencies of
in (2.50) are the lag-dependent cycle frequencies of ![]() . The GACS signal x(t) is said to contain an ACS component (for the given conjugation configuration) if the Lebesgue measure of the set
. The GACS signal x(t) is said to contain an ACS component (for the given conjugation configuration) if the Lebesgue measure of the set ![]() is positive for some
is positive for some ![]() and some
and some ![]() . The GACS signal x(t) is said to be purely GACS or not containing any ACS component if the Lebesgue measure of the set
. The GACS signal x(t) is said to be purely GACS or not containing any ACS component if the Lebesgue measure of the set ![]() is zero
is zero ![]() and
and ![]() . GACS signals containing an ACS component have at least one lag-dependent cycle frequency
. GACS signals containing an ACS component have at least one lag-dependent cycle frequency ![]() which is constant with respect to τ in a set of values of τ with positive Lebesgue measure. A GACS signal containing an ACS component with cycle frequencies
which is constant with respect to τ in a set of values of τ with positive Lebesgue measure. A GACS signal containing an ACS component with cycle frequencies ![]() exhibits spectral components separated by
exhibits spectral components separated by ![]() that are correlated. Analogously, if
that are correlated. Analogously, if ![]() in (2.50) are the lag-dependent cycle frequencies of the cross-moment
in (2.50) are the lag-dependent cycle frequencies of the cross-moment ![]() , then the GACS signals x(t) and y(t) are said to contain a joint ACS component (for the given conjugation configuration) when the Lebesgue measure of the set
, then the GACS signals x(t) and y(t) are said to contain a joint ACS component (for the given conjugation configuration) when the Lebesgue measure of the set ![]() is positive for some
is positive for some ![]() and some
and some ![]() . The GACS signals x(t) and y(t) are said to be jointly purely GACS or not containing any joint ACS component if the Lebesgue measure of the set
. The GACS signals x(t) and y(t) are said to be jointly purely GACS or not containing any joint ACS component if the Lebesgue measure of the set ![]() is zero
is zero ![]() and
and ![]() .
.
In the following, the relationship
(2.51) ![]()
will be used for all values of τ such that there is no equality among different lag-dependent cycle frequencies (see (2.12), (2.19), and Fact 2.2.8). For these values of τ, symmetry relations involving (conjugate) cyclic autocorrelation functions, (conjugate) generalized cyclic autocorrelation functions, and (conjugate) lag-dependent cycle frequencies are derived.
Fact 2.2.18 For the conjugation configuration ![]() (autocorrelation) we have
(autocorrelation) we have
Moreover, the set (see (2.13) and (2.15))
(2.53a) ![]()
(2.53b) 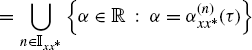
is symmetric in the sense that
Finally, ![]() possibly coincident such that
possibly coincident such that
In the special case of ACS processes, we have, that for the conjugation configuration ![]() the countable set A defined in (2.14) is symmetric in the sense that
the countable set A defined in (2.14) is symmetric in the sense that ![]() .
.
Proof: See Section 3.1.
Fact 2.2.19 For the conjugation configurations ![]() and
and ![]() , we have
, we have
![]() and
and ![]() such that
such that
Proof: See Section 3.1.
Fact 2.2.20 For the conjugation configurations xx (conjugate correlation) and ![]() , we have
, we have
![]() and
and ![]() such that
such that
Proof: See Section 3.1.
2.2.3 Second-Order Spectral Characterization
The presence of sums of Kronecker deltas depending on τ in the expressions of the (conjugate) cyclic autocorrelation function and of the cyclic cross-correlation function of (jointly) GACS processes (see (2.21) and (2.39)) when ![]() has zero Lebesgue measure, does not allow a spectral characterization of GACS processes in terms of ordinary Fourier transforms of these functions.
has zero Lebesgue measure, does not allow a spectral characterization of GACS processes in terms of ordinary Fourier transforms of these functions.
In Section 2.2.2, it is shown that the time-averaged autocorrelation function ![]() is discontinuous in
is discontinuous in ![]() and contains the additive term
and contains the additive term ![]() , where
, where ![]() is the time-averaged power of x(t). That is, the time-averaged autocorrelation function admits the decomposition
is the time-averaged power of x(t). That is, the time-averaged autocorrelation function admits the decomposition
(2.63) ![]()
with ![]() , and
, and ![]() definite nonnegative and possibly discontinuous.
definite nonnegative and possibly discontinuous.
The Fourier transform of ![]() , defined in terms of Lebesgue integral, provides an identically zero function. Consequently, the power spectrum for GACS processes (that are not ACS) cannot be defined in the ordinary sense. However, an heuristic approach to provide a spectral characterization of GACS processes can be based on the μ functional defined in Section 3.2. Specifically, the power spectrum of x(t) can be obtained accounting for the Fourier pair in (3.30). We formally have
, defined in terms of Lebesgue integral, provides an identically zero function. Consequently, the power spectrum for GACS processes (that are not ACS) cannot be defined in the ordinary sense. However, an heuristic approach to provide a spectral characterization of GACS processes can be based on the μ functional defined in Section 3.2. Specifically, the power spectrum of x(t) can be obtained accounting for the Fourier pair in (3.30). We formally have
(2.64) ![]()
where B(f) is the Fourier transform of ![]() . Due to the presence of the term
. Due to the presence of the term ![]() , a quota of the power of x(t) is spread over an infinite bandwidth. In fact, μ(f) can be interpreted as the limit of a very tiny and large rectangular window with unit area (Section 3.2). Consequently, low-pass or band-pass filtering (with finite or essentially finite bandwidth) of GACS signals cancels in the output signal the power contribution
, a quota of the power of x(t) is spread over an infinite bandwidth. In fact, μ(f) can be interpreted as the limit of a very tiny and large rectangular window with unit area (Section 3.2). Consequently, low-pass or band-pass filtering (with finite or essentially finite bandwidth) of GACS signals cancels in the output signal the power contribution ![]() . In particular, if the process is purely GACS, the output signal is zero-power (Sections 2.3 and 2.7.7). This spectral characterization agrees with the observation in (Wiener 1949, pp. 39–40) that if the time-averaged autocorrelation function is discontinuous in the origin, then “there is a portion of the energy which does not belong to any finite frequencies, and which in a certain sense we must associate with infinite frequencies.”
. In particular, if the process is purely GACS, the output signal is zero-power (Sections 2.3 and 2.7.7). This spectral characterization agrees with the observation in (Wiener 1949, pp. 39–40) that if the time-averaged autocorrelation function is discontinuous in the origin, then “there is a portion of the energy which does not belong to any finite frequencies, and which in a certain sense we must associate with infinite frequencies.”
In (Izzo and Napolitano 1998a, 2002a, 2005), it is shown that a useful spectral characterization of (jointly) GACS processes can be obtained by considering the Fourier transforms of the generalized (conjugate) cyclic autocorrelation functions and of the generalized cyclic cross-correlation functions
and analogously for ![]() . As already observed, if
. As already observed, if ![]() has zero Lebesgue measure
has zero Lebesgue measure ![]() , the function defined in (2.65) is not a spectral cross-correlation density function as it happens for ACS processes. In the following, the second-order spectral characterization is made resorting to the Loève bifrequency spectrum.
, the function defined in (2.65) is not a spectral cross-correlation density function as it happens for ACS processes. In the following, the second-order spectral characterization is made resorting to the Loève bifrequency spectrum.
Definition 2.2.21 Let ![]() be a complex-valued second-order harmonizable stochastic process. The Loève bifrequency spectrum (Loève 1963) or spectral correlation function is defined as (Definition 4.2.3 and (1.13))
be a complex-valued second-order harmonizable stochastic process. The Loève bifrequency spectrum (Loève 1963) or spectral correlation function is defined as (Definition 4.2.3 and (1.13))
In (2.66),
(2.67) ![]()
is the Fourier transform of ![]() and is assumed to exist (at least) in the sense of distributions (Gelfand and Vilenkin 1964, Chapter 3), (Henniger 1970). Superscript (*) denotes an optional complex conjugation.
and is assumed to exist (at least) in the sense of distributions (Gelfand and Vilenkin 1964, Chapter 3), (Henniger 1970). Superscript (*) denotes an optional complex conjugation.
A stochastic process is said to be (strongly) harmonizable if it can be expressed as a Fourier-Stieltjes transform of a second-order spectral function with bounded-variation covariance (Loève 1963). A covariance function is said to be harmonizable if it can be expressed as a Fourier-Stieltjes transform of a (spectral) covariance function of bounded variation (Loève 1963). In (Loève 1963, p. 474), it is shown that a necessary condition for a stochastic process to be harmonizable is that it is second-order continuous. In fact, the bounded variation condition on the spectral covariance function implies that harmonizable stochastic processes are continuous in quadratic mean and harmonizable covariances are continuous and bounded. Moreover, since convergence of integrals is considered in the mean-square sense (Definition 2.2.14 and Theorem 2.2.15), in (Loève 1963, p. 476) it is shown that a stochastic process is harmonizable if and only if its covariance function is harmonizable. From Theorem 2.2.13 it follows that GACS processes are not mean-square continuous, and, hence, not (strongly) harmonizable. Consequently, for GACS processes the convergence of the integral
with
(2.69) ![]()
and with (−) denoting an optional minus sign linked to the optional complex conjugation (*), cannot be in the mean-square sense.
Convergence of the integral in (2.68) when ![]() has no bounded variation can be considered in the sense of (Kolmogorov 1960) or in the sense of Morse-Transue (Morse and Transue 1956), (Rao 2008) and the process is said weakly harmonizable. Such an analysis, however, is beyond the scope of this book. In the following, a formal expression for the Loève bifrequency spectrum of a GACS process is derived, even if the process is not strongly harmonizable, without specifying the kind of convergence of the involved integrals.
has no bounded variation can be considered in the sense of (Kolmogorov 1960) or in the sense of Morse-Transue (Morse and Transue 1956), (Rao 2008) and the process is said weakly harmonizable. Such an analysis, however, is beyond the scope of this book. In the following, a formal expression for the Loève bifrequency spectrum of a GACS process is derived, even if the process is not strongly harmonizable, without specifying the kind of convergence of the involved integrals.
Theorem 2.2.22 Loève Bifrequency Spectrum of GACS Processes. Let ![]() be a complex-valued GACS stochastic process. Its Loève bifrequency spectrum is given by
be a complex-valued GACS stochastic process. Its Loève bifrequency spectrum is given by
where the lag-dependent cycle frequencies curves have been chosen so that the set ![]() can be partitioned as
can be partitioned as ![]() , where
, where
![]() is the inverse function of
is the inverse function of ![]() and
and
(2.73) ![]()
are Fourier transforms of those (conjugate) generalized cyclic autocorrelation functions that are coincident with (conjugate) cyclic autocorrelation functions. That is, ![]() , are the (conjugate) cyclic spectra of the ACS component.
, are the (conjugate) cyclic spectra of the ACS component.
Proof: See Section 3.2.
Thus, the Loève bifrequency spectrum of a GACS process contains an impulsive part corresponding to the ACS component and a continuous part corresponding to the purely GACS component. In (Soedjack 2002) it is shown that the continuous term of the Loève bifrequency spectrum cannot be consistently estimated starting from a single realization or sample path, but only using several realizations.
2.2.4 Higher-Order Statistics
In this section, the higher-order characterization of GACS processes is provided in terms of moments and cumulants in the time domain. An extensive treatment on higher-order statistics of GACS signals in the functional (or nonstochastic) approach is made in (Izzo and Napolitano 1998a, 2002a, 2005).
Let ![]() , be N continuous-time complex-valued stochastic processes. Since the
, be N continuous-time complex-valued stochastic processes. Since the ![]() are arbitrary, without lack of generality in this section we can avoid considering (optional) complex conjugations.
are arbitrary, without lack of generality in this section we can avoid considering (optional) complex conjugations.
Definition 2.2.23 The Nth-order temporal cross-moment function (TCMF) of the (complex-valued) processes ![]() is defined as
is defined as
(2.74) 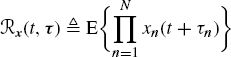
where ![]() and
and ![]() , with
, with ![]() .
.
Definition 2.2.24 The processes ![]() are said to be jointly GACS (for the moment) if their Nth-order TCMF is almost-periodic in t in the sense of Bohr (Bohr 1933, par. 84–92) or, equivalently, uniformly almost periodic in sense of Besicovitch (Besicovitch 1932, Chapter 1), (Corduneanu 1989). That is, for each fixed
are said to be jointly GACS (for the moment) if their Nth-order TCMF is almost-periodic in t in the sense of Bohr (Bohr 1933, par. 84–92) or, equivalently, uniformly almost periodic in sense of Besicovitch (Besicovitch 1932, Chapter 1), (Corduneanu 1989). That is, for each fixed ![]() , is the limit of a uniformly convergent sequence of trigonometric polynomials in t which can be written in the two following equivalent forms (Izzo and Napolitano 1998a, 2002a):
, is the limit of a uniformly convergent sequence of trigonometric polynomials in t which can be written in the two following equivalent forms (Izzo and Napolitano 1998a, 2002a):
In (2.75a), the real numbers α and the complex-valued functions ![]() , referred to as Nth-order (cross-moment) cycle frequencies and cyclic temporal cross-moment functions, are the frequencies and coefficients, respectively, of the generalized Fourier series expansion of
, referred to as Nth-order (cross-moment) cycle frequencies and cyclic temporal cross-moment functions, are the frequencies and coefficients, respectively, of the generalized Fourier series expansion of ![]() that is,
that is,
(2.76) 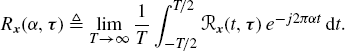
Furthermore, in (2.75a) and (2.75b),
(2.77a) ![]()
(2.77b) ![]()
is a countable set, ![]() is also countable, the real-valued functions
is also countable, the real-valued functions ![]() are referred to as (cross-moment) lag-dependent cycle frequencies and the complex-valued functions
are referred to as (cross-moment) lag-dependent cycle frequencies and the complex-valued functions ![]() , referred to as generalized cyclic cross-moment functions, are defined as
, referred to as generalized cyclic cross-moment functions, are defined as
(2.78) ![]()
for all values of ![]() such that two different N-dimensional varieties described by two different lag-dependent cycle frequencies do not intersect (Izzo and Napolitano 2002a), (Napolitano 2007a). It can be shown that (Izzo and Napolitano 1998a, 2002a)
such that two different N-dimensional varieties described by two different lag-dependent cycle frequencies do not intersect (Izzo and Napolitano 2002a), (Napolitano 2007a). It can be shown that (Izzo and Napolitano 1998a, 2002a)
(2.79) ![]()
where ![]() denotes Kronecker delta, that is,
denotes Kronecker delta, that is, ![]() . That is, the N-dimensional varieties
. That is, the N-dimensional varieties ![]() with
with ![]() describe the support of the cyclic cross-moment function
describe the support of the cyclic cross-moment function ![]() in the N-dimensional
in the N-dimensional ![]() -space.
-space.
More generally, N processes ![]() are said to exhibit joint Nth-order generalized almost-cyclostationarity (for the moment) if the Nth-order TCMF is constituted by a (uniformly) almost-periodic component plus a residual term not containing any finite-strength additive sinewave component (Napolitano and Tesauro 2011):
are said to exhibit joint Nth-order generalized almost-cyclostationarity (for the moment) if the Nth-order TCMF is constituted by a (uniformly) almost-periodic component plus a residual term not containing any finite-strength additive sinewave component (Napolitano and Tesauro 2011):
with
(2.81) 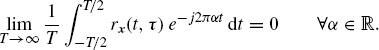
That is, ![]() is an almost-periodic function in the sense of Hartman and Ryll-Nardzewski (Section 1.2.5).
is an almost-periodic function in the sense of Hartman and Ryll-Nardzewski (Section 1.2.5).
Processes with statistical functions constituted by an almost-periodic component plus a residual term are appropriate models in mobile communications. For example, a multipath Doppler channel, that is a multipath channel introducing scaling amplitude, phase, time-delay, frequency shift, and time-scale factor for each path, excited by an ACS or GACS signal, has output with ACS-or GACS-kind statistical functions with residual terms, provided that the time-scale factors of at least two paths are different (Section 7.7.2) (Izzo and Napolitano 2002b).
In (Gardner and Spooner 1994), it is shown that for ACS signals, temporal cumulants, rather than temporal moments, properly describe the possible Nth-order almost-cyclostationarity of signals since computing cumulants is equivalent to removing all the sinewaves generated by beats of lower-order lag products whose orders sum to N. These considerations can easily be extended to GACS signals (Izzo and Napolitano 1998a, 2005).
Definition 2.2.25 The Nth-order temporal cross-cumulant function (TCCF) of the (complex-valued) processes ![]() is defined as
is defined as
(2.82a) 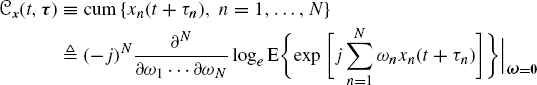
where ![]() with
with ![]() ; P is the set of distinct partitions of
; P is the set of distinct partitions of ![]() , each constituted by the subsets
, each constituted by the subsets ![]() is the
is the ![]() -dimensional vector whose components are those of x having indices in
-dimensional vector whose components are those of x having indices in ![]() , with
, with ![]() the number of elements in
the number of elements in ![]() . See Section 1.4.2 for a discussion of the definition of (cross-) cumulant of complex random variables and processes.
. See Section 1.4.2 for a discussion of the definition of (cross-) cumulant of complex random variables and processes.
Definition 2.2.26 The processes ![]() are said to be jointly GACS (for the cumulant) if their Nth-order TCCF is almost-periodic in t in the sense of Bohr (Bohr 1933), par. 84–92) or, equivalently, uniformly almost periodic in sense of Besicovitch (Besicovitch 1932, Chap. 1), (Corduneanu 1989). That is, for each fixed
are said to be jointly GACS (for the cumulant) if their Nth-order TCCF is almost-periodic in t in the sense of Bohr (Bohr 1933), par. 84–92) or, equivalently, uniformly almost periodic in sense of Besicovitch (Besicovitch 1932, Chap. 1), (Corduneanu 1989). That is, for each fixed ![]() is the limit of a uniformly convergent sequence of trigonometric polynomials in t which can be written in the two following equivalent forms (Izzo and Napolitano 1998a, 2002a):
is the limit of a uniformly convergent sequence of trigonometric polynomials in t which can be written in the two following equivalent forms (Izzo and Napolitano 1998a, 2002a):
In (2.83a), the real numbers β and the complex-valued functions ![]() , referred to as Nth-order (cross-cumulant) cycle frequencies and cyclic temporal cross-cumulant functions, are the frequencies and coefficients, respectively, of the generalized Fourier series expansion of
, referred to as Nth-order (cross-cumulant) cycle frequencies and cyclic temporal cross-cumulant functions, are the frequencies and coefficients, respectively, of the generalized Fourier series expansion of ![]() that is,
that is,
(2.84) 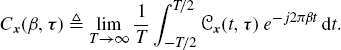
Furthermore, in (2.83a) and (2.83b),
(2.85a) ![]()
(2.85b) ![]()
is a countable set, ![]() is also countable, the real-valued functions
is also countable, the real-valued functions ![]() are referred to as (cross-cumulant) lag-dependent cycle frequencies and the complex-valued functions
are referred to as (cross-cumulant) lag-dependent cycle frequencies and the complex-valued functions ![]() , referred to as generalized cyclic cross-cumulant functions, are defined as
, referred to as generalized cyclic cross-cumulant functions, are defined as
(2.86) ![]()
for all values of ![]() such that two different N-dimensional varieties described by two different lag-dependent cycle frequencies do not intersect (Izzo and Napolitano 2002a), (Napolitano 2007a). It can be shown that (Izzo and Napolitano 1998a, 2002a)
such that two different N-dimensional varieties described by two different lag-dependent cycle frequencies do not intersect (Izzo and Napolitano 2002a), (Napolitano 2007a). It can be shown that (Izzo and Napolitano 1998a, 2002a)
(2.87) ![]()
That is, the N-dimensional varieties ![]() with
with ![]() , describe the support of the cyclic cross-cumulant function
, describe the support of the cyclic cross-cumulant function ![]() in the N-dimensional
in the N-dimensional ![]() -space.
-space.
The Nth-order cyclic temporal cross-cumulant function ![]() can be expressed in terms of Nth-and lower-order cyclic temporal cross-moment functions as (Izzo and Napolitano 1998a)
can be expressed in terms of Nth-and lower-order cyclic temporal cross-moment functions as (Izzo and Napolitano 1998a)
where ![]() are the cycle frequencies of the temporal cross-moment function of
are the cycle frequencies of the temporal cross-moment function of ![]() , and the second sum is extended over all vectors
, and the second sum is extended over all vectors ![]() such that
such that ![]() . Equation (2.88) extends to GACS processes a known result for ACS processes (Gardner and Spooner 1994).
. Equation (2.88) extends to GACS processes a known result for ACS processes (Gardner and Spooner 1994).
In (Izzo and Napolitano 1998a, 2005), it is shown that the set of the Nth-order cumulant cycle frequencies is contained in the set of the Nth-order moment cycle frequencies. That is
(2.89) ![]()
More generally, for processes exhibiting Nth-order generalized almost-cyclostationarity the temporal cross-cumulant function is constituted by an almost-periodic component plus a residual term not containing any additive finite-strength sinewave component (Napolitano and Tesauro 2011):
with
(2.91) 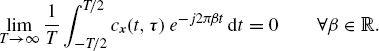
That is, ![]() is an almost-periodic function in the sense of Hartman and Ryll-Nardzewski (Section 1.2.5).
is an almost-periodic function in the sense of Hartman and Ryll-Nardzewski (Section 1.2.5).
2.2.5 Processes with Almost-Periodic Covariance
In this section, processes with almost-periodic covariance function are briefly reviewed and their link with GACS processes is enlightened.
A continuous-time complex-valued process x(t) is said to be a process with almost-periodic covariance (Lii and Rosenblatt 2006) if
By making the variable change ![]() (hence
(hence ![]() ) in the left-hand side of (2.92), we get
) in the left-hand side of (2.92), we get
(2.93) ![]()
where the right-hand side is obtained by using (2.92) with the replacements ![]() ,
, ![]() , and
, and ![]() . Thus, every process with almost-periodic covariance can be reduced to a second-order wide-sense GACS process by a time-variable change.
. Thus, every process with almost-periodic covariance can be reduced to a second-order wide-sense GACS process by a time-variable change.
A continuous-time complex-valued process x(t) is said to be with covariance almost-periodic of two variables (Swift 1996) if
(2.94) ![]()
An almost-periodic stochastic process
(2.95) ![]()
with xk correlated random variables such that ![]() has a covariance almost-periodic of two variables.
has a covariance almost-periodic of two variables.
2.2.6 Motivations and Examples
In this section, motivations for adopting the GACS model and examples of GACS processes are presented. Applications to communications, radar, and sonar are treated in Chapter 7.
2.2.6.1 Doppler Channel due to Radial Acceleration
The GACS model turns out to be appropriate in mobile communications systems when the channel cannot be modeled as almost-periodically time-variant (Izzo and Napolitano 2002a,b). For example, the output y(t) of the Doppler channel existing between transmitter and receiver with nonzero relative radial acceleration is GACS when the input signal x(t) is ACS (Izzo and Napolitano 2002b) (Sections 7.4, 7.5.2, 7.8).
Let
(2.96) ![]()
be the transmitted signal. In the case of relative motion between transmitter and receiver, under mild assumptions the received signal can be written as (Section 7.1)
(2.97) 
where a is attenuation and D(t) is time-varying delay. In the case of transmitter and receiver with constant relative radial acceleration, the delay is quadratically time-varying (Section 7.4), (Kelly and Wishner 1965), (Rihaczek 1967):
(2.98) ![]()
Under the “narrow-band” approximation, the time-varying component of the delay in the complex envelope x(t − D(t)) can be ignored (Section 7.5.2) (Kelly and Wishner 1965) obtaining the chirp-modulated signal:
where ![]() is the complex gain,
is the complex gain, ![]() the frequency shift, and
the frequency shift, and ![]() the chirp rate. The autocorrelation function of y(t) is (Section 7.8)
the chirp rate. The autocorrelation function of y(t) is (Section 7.8)
If x(t) is ACS, that is,
(2.101) ![]()
where ![]() is a countable set and
is a countable set and ![]() is the set of cycle frequencies, (2.100) specializes into
is the set of cycle frequencies, (2.100) specializes into
(2.102) ![]()
That is, y(t) is GACS with autocorrelation function
(2.103) ![]()
lag dependent cycle frequencies
generalized cyclic autocorrelation functions
(2.105) ![]()
and cyclic autocorrelation function
In the figures, supports are drawn as “checkerboard” plots where gray levels represent magnitude of generalized cyclic autocorrelation functions.
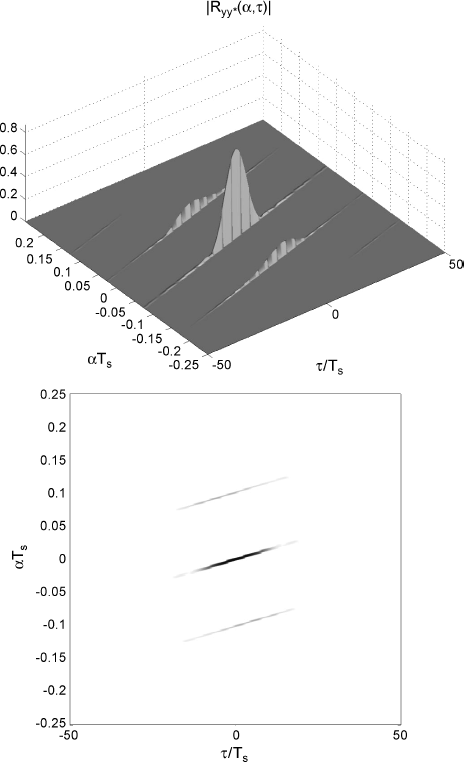
In Figures 2.2 and 2.3, the magnitude and the support of the cyclic autocorrelation function, as a function of α and τ, for both the input x(t) and the output y(t) are reported for x(t) PAM signal with raised cosine pulse and stationary-white binary modulating sequence. The signal x(t) is cyclostationary with cycle frequencies ![]() (Gardner 1985), where Tp is the symbol period, and the support of the cyclic autocorrelation function is constituted by lines parallel to the τ axis (Figure 2.2 (bottom)). In contrast, the signal y(t) is GACS with cyclic autocorrelation function whose support is described by the lag-dependent cycle frequencies ηn(τ) which are parallel lines with slope γ in the (α, τ) plane (Figure 2.3 (bottom)). Thus, they do not intersect each other. In Figures 2.2 and 2.3,
(Gardner 1985), where Tp is the symbol period, and the support of the cyclic autocorrelation function is constituted by lines parallel to the τ axis (Figure 2.2 (bottom)). In contrast, the signal y(t) is GACS with cyclic autocorrelation function whose support is described by the lag-dependent cycle frequencies ηn(τ) which are parallel lines with slope γ in the (α, τ) plane (Figure 2.3 (bottom)). Thus, they do not intersect each other. In Figures 2.2 and 2.3, ![]() , with Ts the sampling period, and a raised cosine pulse with excess bandwidth
, with Ts the sampling period, and a raised cosine pulse with excess bandwidth ![]() is considered.
is considered.
Figure 2.2 ACS input and GACS output of the Doppler channel existing between transmitter and receiver with constant relative radial acceleration. (Top) Magnitude and (bottom) support of the cyclic autocorrelation function ![]() , as a function of
, as a function of ![]() and
and ![]() , of the input ACS signal x(t).
, of the input ACS signal x(t).
Source: (Napolitano 2007a) © IEEE
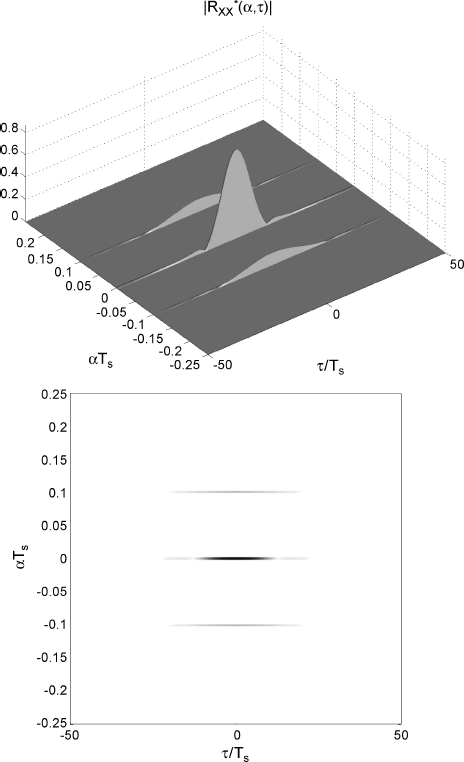
Figure 2.3 ACS input and GACS output of the Doppler channel existing between transmitter and receiver with constant relative radial acceleration. (Top) magnitude and (bottom) support of the cyclic autocorrelation function ![]() , as a function of
, as a function of ![]() and
and ![]() , of the output GACS signal y(t).
, of the output GACS signal y(t).
Source: (Napolitano 2007a) © IEEE
2.2.6.2 Communications Signals with Time-Varying Parameters
The GACS model is appropriate to describe communications signals with parameters, such as carrier frequency or baud rate, that are slowly varying functions of time. Specifically, in communications problems, signals can be modeled as ACS or GACS depending on the data-record length. In fact, if the data-record length is increased too much (e.g., in order to gain a better immunity against the effects of noise and interference), it can happen that the ACS model for the input signal is no longer appropriate but, rather, a GACS model needs to be considered since possible time variations of timing parameters of the signals (not evidenced with smaller data-record length) must be taken into account (Izzo and Napolitano 1998a, 2005). Consequently, increasing too much the data-record length without changing the statistical model for the signal, does not have, for example, the beneficial effect of improving the reliability of the signal cyclic statistic estimates but, rather, gives rise to biased cyclic statistics (Izzo and Napolitano 1998a, 2002b). Therefore, there exists an upper limit to the maximum usable data-record length and, consequently, there exists a limit to the minimum acceptable signal-to-noise ratio for cyclostationarity-based algorithms which are, in principle, intrinsically immune to the effects of noise and interference, provided that the data-record length approaches infinity. This fact puts some limitations on the performance obtainable with some signal processing algorithms adopted in communication applications where communications signals are modeled as ACS and constitutes a motivation to consider the class of the GACS signals.
Examples of communications signals with time-varying parameters that can be modeled as GACS are nonuniformly sampled signals (Izzo and Napolitano 1998a, 2002b, 2005) and modulated signals with sinusoidally-varying carrier frequency (Section 7.9.3). The former can be expressed as
(2.107) ![]()
where p(t) is a finite-energy pulse and ![]() is a slowly time-varying sampling period, and the latter can be written as
is a slowly time-varying sampling period, and the latter can be written as
(2.108) ![]()
where ![]() and, in both examples,
and, in both examples, ![]() is a stationary or ACS signal.
is a stationary or ACS signal.