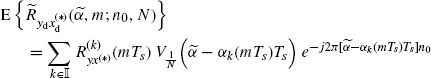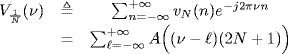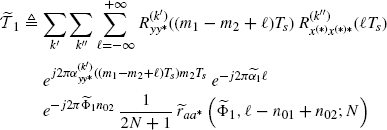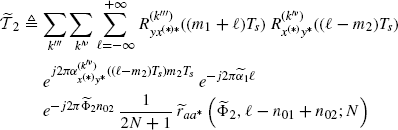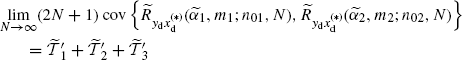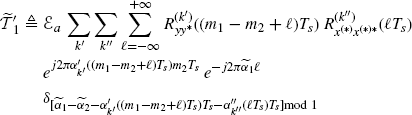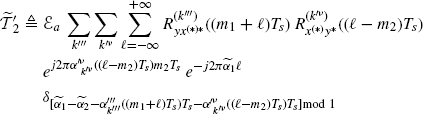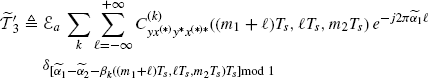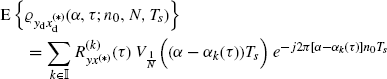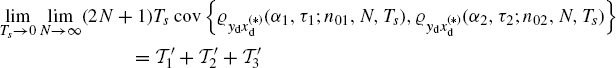2.6 Discrete-Time Estimator of the Cyclic Cross-Correlation Function

In this section, the discrete-time cyclic cross-correlogram of the discrete-time process obtained by uniformly sampling a continuous-time GACS process is shown to be a mean-square consistent and asymptotically complex Normal estimator of the continuous-time cyclic cross-correlation function as the data-record length approaches infinity and the sampling period approaches zero (Napolitano 2009).

Note that the results of Section 2.6 for discrete-time processes cannot be obtained straightforwardly by substituting integrals with sums into the results of Sections 2.4.1 –2.4.3 which have been obtained for continuous-time processes as is made, in the stationary case, in (Brillinger and Rosenblatt 1967).

2.6.1 Discrete-Time Cyclic Cross-Correlogram

In this section, the discrete-time cyclic cross-correlogram is defined and its mean and covariance are evaluated for finite number of samples and sampling period.

Definition 2.6.1 Let y_d(n) and x_d(n) be the discrete-time processes defined in (2.172). Their discrete-time cyclic cross-correlogram (DT-CCC) at cycle frequency is defined as

(2.181)

where

(2.182)

is a data-tapering window nonzero in { − N, ..., N}, with a(t) as in Assumption 2.4.5.

Note that since a(t) has finite width, the infinite sum in (2.181) is in fact a finite sum from n₀ − N to n₀ + N.

By taking the expected value of the DT-CCC (2.181) and using (2.174c), the following result is obtained, where the assumptions allow to interchange the order of sum and expectation operations and the order of double-index sums.

Theorem 2.6.2 Expected Value of the Discrete-Time Cyclic Cross-Correlogram (Napolitano 2009, Theorem 5.1). Let x_d(n) and y_d(n) be the discrete-time processes defined in (2.172). Under Assumptions 2.4,2a (uniformly almost-periodic statistics), 2.4.3a (Fourier series regularity), and 2.4.5 (data-tapering window regularity) on the continuous-time processes x(t) and y(t), the expected value of the DT-CCC (2.181) is given by

(2.183)

where

(2.184)

with A(f) Fourier transform of a(t).

Proof: See Section 3.9.

The function V_1/N(ν) is periodic with period 1 and has bandwidth of the order of 1/N. Consequently, the cycle-frequency resolution is of the order of 1/N and aliasing in the cycle-frequency domain occurs. Specifically, from (2.183) it follows that in the -domain the expected value of the DT-CCC can be significantly different from zero within intervals of width 1/N parallel to the axis and centered in the points with , . 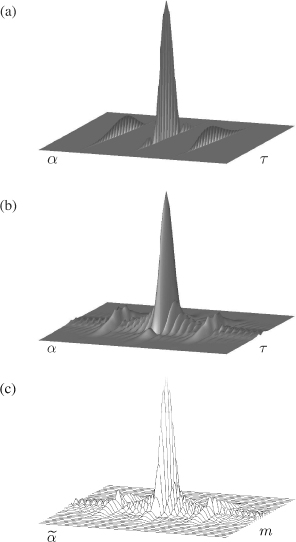Such points correspond to scaled and aliased samples of the lag-dependent cycle frequency curves α = α_k(τ), that is, the support curves of the continuous-time cyclic cross-correlation function (see Figure 2.4a, where the magnitude of the cyclic autocorrelation function of the continuous-time chirp modulated PAM signal of Section 2.2.6 is represented). Moreover, the expected value at is due essentially to all lag-dependent cycle frequencies α_k(τ), such that

(2.185)

for some integer p and some . That is, a leakage phenomenon among lag-dependent cycle-frequency curves which are sufficiently close (modulo f_s) to each other occurs (Figure 2.4c) (see also the discussion following Theorem 2.4.6 for the continuous-time estimator). Therefore, both aliasing and cyclic leakage effects are present. The effect of cyclic leakage becomes negligible as N→ ∞ and the effect of aliasing becomes negligible as T_s → 0. In contrast, in the expected value of the continuous-time cyclic cross-correlogram, only cyclic leakage, without aliasing in the cycle frequency domain, is present (Figure 2.4b).

By expressing the covariance of the lag-product in terms of second-order moments and a fourth-order cumulant, the following result can be proved, where the assumptions allow to interchange the order of sum and expectation operators and the order of multiple-index sum operations.

Theorem 2.6.3 Covariance of the Discrete-Time Cyclic Cross-Correlogram (Napolitano 2009, Theorem 5.2). Let x_d(n) and y_d(n) be discrete-time zero-mean processes defined in (2.172). Under Assumptions 2.4.2 (uniformly almost-periodic statistics), 2.4.3 (Fourier series regularity), and 2.4.5 (data-tapering window regularity) on the continuous-time processes x(t) and y(t), the covariance of the DT-CCC (2.181) is given by

(2.186)

where

(2.187)

(2.188)

(2.189)

with

(2.190)

(2.191)

(2.192)

(2.193)

Proof: See Section 3.9.

2.6.2 Asymptotic Results as N→ ∞

In this section, the asymptotic (N→ ∞) expected value and covariance of the DT-CCC are determined and its asymptotic complex Normality is proved.

Theorem 2.6.4 Asymptotic Expected Value of the Discrete-Time Cyclic Cross-Correlogram (Napolitano 2009, Theorem 6.1). Let x_d(n) and y_d(n) be the discrete-time processes defined in (2.172). Under Assumptions 2.4.2a (uniformly almost-periodic statistics), 2.4.3a (Fourier series regularity), and 2.4.5 (data-tapering window regularity) on the continuous-time processes x(t) and y(t), the asymptotic (N→ ∞) expected value of the DT-CCC (2.181) is given by

(2.194)

Proof: See Section 3.10.

Theorem 2.6.5 Asymptotic Covariance of the Discrete-Time Cyclic Cross-Correlogram (Napolitano 2009, Theorem 6.2). Let x_d(n) and y_d(n) be discrete-time zero-mean processes defined in (2.172). Under Assumptions 2.4.2 (uniformly almost-periodic statistics), 2.4.3 (Fourier series regularity), 2.4.5 (data-tapering window regularity), and 2.4.8 (mixing conditions (I)) on the continuous-time processes x(t) and y(t), the asymptotic (N→ ∞) covariance of the DT-CCC (2.181) is given by

(2.195)

where

(2.196)

(2.197)

(2.198)

with if and otherwise, and

(2.199)

In (2.196)–(2.198), for notation simplicity, , , , and .

Proof: See Section 3.10.

From Theorem 2.6.4 it follows that the DT-CCC (2.181) is an asymptotically (N→ ∞), unbiased estimator of the discrete-time cyclic cross-correlation function (2.173). Moreover, from Theorem 2.6.5 it follows that the variance of the DT-CCC asymptotically vanishes. Consequently, the DT-CCC is a mean-square consistent estimator of the discrete-time cyclic cross-correlation function, that is, of an aliased version of the continuous-time cyclic cross-correlation function (see (2.179a)).

In order to establish the rate of convergence to zero of the bias of the DT-CCC and its asymptotic Normality, the following assumption of lack of clusters (accumulation points) of cycle frequencies is needed.

Assumption 2.6.6 Lack of Support Curve Clusters (II). For every m, the set defined in (2.180) does not contain any cluster of cycle frequencies. That is, let

(2.200)

then, for every , no curve α_k(τ) is such that the value [α_k(mT_s)T_s] mod 1 can be arbitrarily close to the cycle frequency . Thus, for every and m it results that

(2.201)

The set is finite or at most countable and is the set of indices k such that, for the fixed , m, and T_s we have for some . Assumption 2.6.6 means that the greatest lower bound (G.L.B.) or infimum of the distances is nonzero for every and . That is, the point is not a cluster of cycle frequencies. A sufficient condition assuring this is that the number of lag-dependent cycle frequencies is finite, that is, is finite (see, e.g., the chirp-modulated PAM signal with raised cosine pulse in Section 2.2.6).

In the following, where necessary, the very mild assumption that for every fixed k the lag-dependent cycle frequency α_k(τ) is bounded for finite τ will be made.

Let γ be the rate of decay to zero of A(f) as specified in Assumption 2.4.5. We have the following result.

Theorem 2.6.7 Rate of Convergence of the Bias of the Discrete-Time Cyclic Cross-Correlogram (Napolitano 2009, Theorem 6.3). Let x_d(n) and y_d(n) be the discrete-time processes defined in (2.172). Under Assumptions 2.4.2a (uniformly almost-periodic statistics), 2.4.3a (Fourier series regularity), 2.4.5 (data-tapering window regularity), and 2.6.6 (lack of support curve clusters (II)), on the continuous-time processes x(t) and y(t), and provided that γ > 1 (or γ = 1 in the special case of a(t) = rect(t)), one obtains

(2.202)

Proof: See Section 3.10.

In the following, the asymptotic (N→ ∞) complex Normality of the DT-CCC will be proved.

Let

(2.203)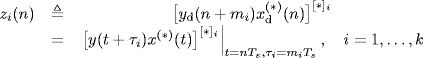

be second-order discrete-time lag-product waveforms, with optional complex conjugations [*]_i, i = 1, ..., k, having kth-order cumulant where the cumulant of complex processes is defined according to (Spooner and Gardner 1994, App. A) (see also Section 1.4.2).

Assumption 2.6.8 Mixing Conditions (IV). For every integer k ≥ 2, , i = 1, ..., k and every conjugation configuration [*]₁, ..., [*]_k, there exists a positive bounded Riemann integrable (and hence also Lebesgue summable) function ϕ(s₁, ..., s_k−1), , (depending on m_i, i = 1, ..., k and the conjugation configuration) such that, for T_s fixed,

(2.204)

uniformly with respect to n.

The function ϕ can be assumed Lebesgue integrable if it is defined in a compact. In fact, there exists a continuous function on the compact (hence Riemann integrable) close as desired to ϕ (Rudin 1987, p. 55) (Lusin Theorem).

Assumption 2.6.8 is the discrete-time counterpart of Assumption 2.4.15. Analogously to the continuous-time case, the cumulant can be expressed as in (2.160). Therefore, Assumption 2.6.8 is satisfied provided that the cumulants up to order 2k of the elements taken from table (2.159) are summable. In addition, as already observed in the continuous-time case, Assumption 2.6.8 is fulfilled if the processes x(t) and y(t) have finite-memory or memory decaying sufficiently fast. Processes of this kind include communications signals with independent and identically distributed (i.i.d.) symbols or block coded symbols, processes with exponentially decaying joint probability density function, and finite-memory (time-variant) transformations of such processes. Moreover, Assumption 2.6.8 turns out to be verified if the stochastic processes z_i(t), i = 1, ..., k are jointly kth-order GACS satisfying condition (2.165).

Analogously to the continuous-time case, the proof of the zero-mean joint complex asymptotic Normality of the random variables

(2.205)

is made in Theorem 2.6.22 showing that asymptotically (N → ∞)

with superscript [*]_h denoting optional complex conjugation. In fact, in Section 1.4.2 it is shown that these are necessary and sufficient conditions for the joint asymptotic Normality of complex random variables, where cumulants of complex random variables are defined according to (Spooner and Gardner 1994, App. A) (see also (1.209) and Section 1.4.2 for a discussion on the usefulness of this definition). Condition 1 follows from Theorem 2.6.7 on the rate of decay to zero of the bias of the DT-CCC. Condition 2a is a consequence of Theorem 2.6.5 on the asymptotic covariance of the DT-CCC. Condition 2b follows from Theorem 3.13.2. Finally, Condition 3 follows from Lemma 2.6.9 on the rate of decay to zero of the joint cumulant of DT-CCCs.

The main assumptions used to prove these theorems and lemmas are regularity of the (generalized) Fourier series of the almost-periodic second-and fourth-order cumulants of the underlying continuous-time GACS processes (Assumptions 2.4.2–2.4.3), short-range statistical dependence of the continuous-time GACS processes expressed in terms of summability of joint cumulants (Assumptions 2.4.8 and 2.6.8), and regularity of the data-tapering window (Assumption 2.4.5). A critical assumption used in the proof of Theorem 2.6.7 is lack of clusters of cycle frequencies of the discrete-time ACS processes (Assumptions 2.6.6). This can be obtained, for example, if the number of lag-dependent cycle frequencies α_k(τ) is finite, that is, if the set is finite.

Several differences exist between the assumptions used to prove the asymptotic properties of the continuous-time estimator (2.118) and those used for the discrete-time estimator (2.181). Specifically, Assumption 2.6.6 is stronger than the analogous Assumption 2.4.10 used to establish the rate of decay to zero of the bias of the continuous-time cyclic cross-correlogram and its asymptotic Normality. In fact, in (2.200) and (2.201) cycle frequencies have to be considered modulo f_s and (2.201) could not be verified if the set defined in (2.180) contains cluster points. In addition, the needed rate of decay to zero of A(f) as |f|→ ∞ is O(|f|^−γ) with γ > 1 (or γ = 1 in the special case of a(t) = rect(t)). In contrast, in the continuous-time case, γ > 1/2 is sufficient (see Theorem 2.4.18). Finally, unlike the continuous-time case, Assumptions 2.4.4 and 2.4.16 on boundedness of moments (used for application of the Fubini and Tonelli theorem) are not needed in the discrete-time case.

Lemma 2.6.9 Rate of Convergence to Zero of Cumulants of Discrete-Time Cyclic Cross-Correlograms (Napolitano 2009, Lemma 6.1). Under Assumptions 2.4.5 (data-tapering window regularity) and 2.6.8 (mixing conditions (IV)) for every k ≥ 2 and > 0 one obtains

(2.206)

Proof: See Section 3.10.

Theorem 2.6.10 Asymptotic Joint Normality of the Discrete-Time Cyclic Cross-Correlograms (Napolitano 2009, Theorem 6.4). Let x_d(n) and y_d(n) be discrete-time zero-mean processes defined in (2.172). Under Assumptions 2.4.2 (uniformly almost-periodic statistics), 2.4.3 (Fourier series regularity), 2.4.5 (data-tapering window regularity), and 2.4.8 (mixing conditions (I)) on the continuous-time processes x(t) and y(t), under Assumptions 2.6.6 (lack of support curve clusters (II)) and 2.6.8 (mixing conditions (IV)) and provided that γ > 1 (or γ = 1 in the special case of a(t) = rect(t)), the random variables defined in (2.205)

are asymptotically (as N→ ∞) zero-mean jointly complex Normal with asymptotic covariance matrix Σ with entries

(2.207)

given by (2.195) and asymptotic conjugate covariance matrix Σ^(c) with entries

(2.208)

given by (3.256).

Proof: See Section 3.10.

2.6.3 Asymptotic Results as N→ ∞ and T_s → 0

In order to obtain a reliable discrete-time estimate of samples of the continuous-time cyclic autocorrelation function, a further assumption is needed in order to control the amount of aliasing in (2.179a) and (2.179b) when the sampling period T_s approaches zero.

Assumption 2.6.11 Aliasing Series Summability. For every and m there exists a sequence of positive numbers independent of T_s such that

A sufficient condition such that Assumption 2.13 is verified is that

(2.209)

with r > 1 uniformly w.r.t. τ. Every GACS process x(t) with a finite number of lag-dependent cycle frequencies and bounded (conjugate) generalized cyclic autocorrelation functions satisfies (2.209) and consequently Assumption 2.6.11 with y ≡ x since only a finite number of nonzero terms is present in the sum over p (see, e.g., the chirp-modulated PAM signal with raised cosine pulse of Section 2.2.6). The case r = 1 in (2.209) (which occurs for example for a PAM signal with rectangular pulse) needs to be treated separately.

Lemma 2.6.12 (Napolitano 2009, Lemma 7.1). Under assumption (2.209) (from which Assumption 2.13 follows) one obtains

(2.210)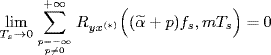

pointwise.

Proof: See Section 3.11.

From Lemma 2.6.12 it follows that the aliasing terms (p ≠ 0) in (2.179a) and (2.179b) can be made arbitrarily small by making the sampling period T_s sufficiently small. Furthermore, from Theorems 2.6.4 and 2.6.5 it follows that, for any fixed T_s, the DT-CCC approaches in the mean-square sense the aliased cyclic cross-correlation function (2.179a)–(2.179b) as the data-record length T = (2N + 1)T_s approaches infinity. Consequently, for T_s sufficiently small and N sufficiently large such that T = (2N + 1)T_s > 1, the DT-CCC , at normalized cycle frequency and normalized lag m = τ/T_s, can be made arbitrarily close to samples of the continuous-time cyclic cross-correlation function in the mean-square sense, provided that τ and α are multiples of T_s and 1/T_s, respectively. Specifically, we have the following result.

Theorem 2.6.13 Mean-Square Consistency of the Discrete-Time Cyclic Cross-Correlogram (Napolitano 2009, Theorem 7.1). Under Assumptions 2.4.2 (uniformly almost-periodic statistics), 2.4.3 (Fourier series regularity), 2.4.5 (data-tapering window regularity), 2.4.8 (mixing conditions (I)), and 2.6.11 (aliasing series summability) (i.e., the assumptions for Theorems 2.6.4, and 2.6.5, and Lemma 2.6.12) one obtains

(2.211)

where the order of the two limits cannot be interchanged and the limit is not necessarily uniform with respect to .

Proof: See Section 3.11.

From Theorem 2.6.13 it follows that the mean-square error between the DT-CCC and samples of the continuous-time cyclic cross-correlation function can be made arbitrarily small, provided that the data-record length is sufficiently large and the sampling period is sufficiently small. However, the asymptotic result of Theorem 2.6.13 has the drawback that, for fixed and m, when T_s → 0 it follows and τ = mT_s → 0. Thus, this analysis turns out to be unhelpful if the asymptotic (as N→ ∞ and T_s → 0) bias and covariance are needed and asymptotic Normality needs to be proved. An asymptotic analysis not suffering from such a drawback can be made starting from the hybrid cyclic cross-correlogram (Napolitano 2009).

Definition 2.6.14 Let y(t) and x(t) be continuous-time processes. The hybrid cyclic cross-correlogram (H-CCC) at cycle frequency and lag of x_d(n) defined as in (2.172) and

(2.212)

is defined as

(2.213)

where is the data-tapering window nonzero in { − N, ..., N} defined in (2.182) (with a(t) as in Assumption 2.4.5).

Note that, unlike the DT-CCC of Definition 2.6.1, the lag parameter τ is not necessarily an integer multiple of T_s, is not assumed to be proportional to T_s, and α is a cycle frequency not normalized to f_s. Consequently, τ can be retained constant as T_s → 0 avoiding the drawback τ → 0 as T_s → 0 as in Theorem 2.6.13. Analogously, the cycle frequency of the continuous-time process does not need to be proportional to the sampling frequency f_s and can be kept constant as f_s→ ∞. It is worthwhile emphasizing that the hybrid cyclic cross-correlogram turns out to be useful just to analytically carry out the asymptotic analysis. In practice, the DT-CCC should be implemented since the available discrete-time samples are y((n + m)T_s). Thus, for a fixed value of τ, when T_s → 0, m should accordingly increase in order to keep constant the product mT_s. Analogously, should accordingly decrease in order to keep constant . Note that, however, the H-CCC can actually be computed by using Definition 3.11.1 of time-shifted discrete-time signal with noninteger time shift and its implementation described in Fact 3.11.2.

The expected value and covariance of the H-CCC can be obtained with minor changes from those of the DT-CCC.

For finite N and T_s, from Theorem 2.6.2 with the replacements and we immediately get the expected value of the H-CCC:

(2.214)

where is defined in (2.184). The function V_1/N(ν) is periodic with period 1 and has a bandwidth of the order of 1/N. Consequently, the cycle-frequency resolution is of the order of 1/(NT_s) and aliasing in the cycle-frequency α domain occurs. Specifically, from (2.214) it follows that the expected value of the H-CCC can be significantly different from zero within strips of width 1/(NT_s) around the curves in the (α, τ)-plane defined by α = α_k(τ) mod f_s, . Moreover, the expected value at (α, τ) is due essentially to all the lag-dependent cycle frequencies α_k(τ) such that

(2.215)

for some integer p and some . That is, a leakage phenomenon among lag-dependent cycle-frequency curves which are sufficiently close (modulo f_s) to each other occurs (see also the discussion following Theorem 2.4.6 for the continuous-time estimator and Theorem 2.6.2 for the DT-CCC).

For finite N and T_s, from Theorem 2.6.3 we obtain the covariance of the H-CCC

(2.216)

where , , and are defined in (2.187), (2.188), and (2.189), respectively, with the replacements τ₁curvearrowrightm₁T_s, , τ₂m₂T_s, , and (defined in (2.190)) substituted by .

The asymptotic results as N→ ∞ for the H-CCC are obtained, with minor changes, as those for the DT-CCC. In particular, result (3.175) of Lemma 3.10.2 should be used.

By reasoning as in Theorem 2.6.4, we have that the asymptotic (N→ ∞) expected value of the H-CCC(2.213) is given by

(2.217a)

(2.217b)

Furthermore, by reasoning as in Theorem 2.6.5, we have that the asymptotic (N→ ∞) covariance of the H-CCC (2.213) is given by

(2.218)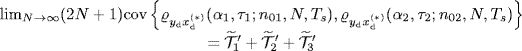

where , , and are defined in (2.196), (2.197), and (2.198), respectively, with the replacements τ₁curvearrowrightm₁T_s, , τ₂m₂T_s, . Finally, the rate of convergence of the bias of the H-CCC as N→ ∞ is obtained by following the guidelines of Theorem 2.6.7:

(2.219)

where γ is the rate of decay to zero of A(f), the Fourier transform of the data-tapering window a(t).

In order to establish the rate of convergence to zero of the bias of the H-CCC and its asymptotic Normality as N→ ∞ and T_s → 0, an assumption on the lack of clusters of cycle frequencies different from Assumption 2.11 is needed. For this purpose, let us define the sets

(2.220)

(2.221a)

(2.221b)

(2.221c)

(strictly speaking, the second equality should be substituted by ⊆).

Assumption 2.6.15 Lack of Support Curve Clusters (III). For every τ, the cycle-frequency set in (2.221c) does not contain any cluster of cycle frequencies. That is, let

(2.222)

then, for every , no curve α_k(τ) is such that the value α_k(τ) mod f_s can be arbitrarily close to the cycle frequency α. Thus, for every α and τ it results that

(2.223)

Assumption 2.6.15 means that there is no cluster of lag-dependent cycle-frequency curves, where cycle frequencies are considered modulo f_s. Thus, it is stronger than Assumption 2.4.10. A sufficient condition assuring that Assumption 2.6.15 is satisfied is that the number of lag-dependent cycle-frequency curves is finite. That is, the set is finite. Note that, Assumption 2.6.15 differs from Assumption 2.6.6 since the definitions of the sets and are different. Specifically, in the former the argument of the functions α_k(·) does not depend on T_s whereas in the latter it does. Such a difference is fundamental in the study of the asymptotic properties as T_s → 0.

In the following, asymptotic results as N→ ∞ and T_s → 0 are provided. Condition N→ ∞ needs to find consistency for the discrete-time estimator, whereas condition T_s → 0 assures lack of aliasing. Note that, in order to have asymptotically an infinitely long data-record length, condition T = (2N+ 1)T_s → ∞ needs to be verified. Consequently, in the following asymptotic results, we have that first N→ ∞ and then T_s → 0, that is, the order of the two limits as N→ ∞ and T_s → 0 cannot be interchanged.

In the sequel, when necessary, the very mild assumption that the lag-dependent cycle frequencies α_k(τ) are bounded for finite τ will be made.

Theorem 2.6.16. Asymptotic Expected Value of the Hybrid Cyclic Cross-Correlogram (Napolitano 2009, Theorem 7.2). Let y(t) and x(t) be wide-sense jointly GACS stochastic processes with cross-correlation function (2.31c). Under Assumptions 2.4.2a (uniformly almost-periodic statistics), 2.4.3a (Fourier series regularity), 2.4.5 (data-tapering window regularity), and 2.6.11 (aliasing series summability), one obtains

(2.224)

where the order of the two limits cannot be interchanged.

Proof: See Section 3.11.

Let A(f) be the Fourier transform of a(t). Under Assumption 2.4.5, there exists γ > 0 such that A(f) = O(|f|^−γ) as |f|→ ∞.

For the bias of the H-CCC

(2.225)

the following result holds.

Theorem 2.6.17. Rate of Convergence of the Bias of the Hybrid Cyclic Cross-Correlogram (Napolitano 2009, Theorem 7.3). Let y(t) and x(t) be wide-sense jointly GACS stochastic processes with cross-correlation function (2.31c). Under Assumptions 2.4.2a (uniformly almost-periodic statistics), 2.4.3a (Fourier series regularity), and 2.4.5 (data-tapering window regularity) assuming that the number of lag-dependent cycle frequencies is finite (so that also Assumptions 2.6.11 (aliasing series summability) and 2.6.15 (lack of support curve clusters (III)) are verified), and provided that γ > 1 (or γ = 1 in the special case of a(t) = rect(t)), one obtains

(2.226)

where the order of the two limits cannot be interchanged.

Proof: See Section 3.11.

Theorem 2.6.28 Asymptotic Covariance of the Hybrid Cyclic Cross-Correlogram (Napolitano 2009, Theorem 7.4). Let y(t) and x(t) be zero-mean wide-sense jointly GACS stochastic processes with cross-correlation function (2.31c). Under Assumptions 2.4.2 (uniformly almost-periodic statistics), 2.4.3 (Fourier series regularity), 2.4.5 (data-tapering window regularity), and 2.4.8 (mixing conditions (I)) (with the sets and finite), the asymptotic (N→ ∞ and T_s → 0 with NT_s→ ∞) covariance of the H-CCC (2.213) is given by

(2.227)

with , and given by (2.147), (2.148), and (2.149) (in Theorem 2.4.13), respectively, where the order of the two limits cannot be interchanged.

Proof: See Section 3.11.

By comparing the results of Theorems 2.4.13 and 2.6.18 it follows that the asymptotic (T→ ∞) covariance of the continuous-time cyclic cross-correlogram and the asymptotic (N→ ∞ and T_s → 0 with NT_s→ ∞) covariance of the H-CCC are coincident. That is,

(2.228)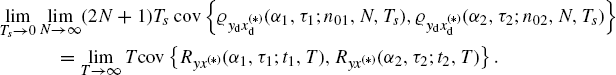

From Theorem 2.6.16 it follows that the H-CCC is an asymptotically (N→ ∞ and T_s → 0 with NT_s→ ∞) unbiased estimator of the continuous-time cyclic cross-correlation function. Moreover, from Theorem 2.6.18 it follows that the H-CCC has asymptotically vanishing variance. Therefore, the H-CCC is a mean-square consistent estimator of the continuous-time cyclic cross-correlation function.

The proof of the zero-mean joint complex asymptotic Normality of the random variables

(2.229)

is given in Theorem 2.6.20 showing that asymptotically (N→ ∞ and T_s → 0 with NT_s→ ∞)

with superscript [*]_h denoting optional complex conjugation. Condition 1 follows from Theorem 2.6.17 on the rate of decay to zero of the bias of the H-CCC. Condition 2a is a consequence of Theorem 2.6.18 on the asymptotic covariance of the H-CCC. Condition 2b follows from Theorem 3.13.3. Finally, Condition 3 follows from Lemma 2.6.19 on the rate of decay to zero of the joint cumulant of H-CCCs.

Lemma 2.6.19 Rate of Convergence to Zero of Cumulants of Hybrid Cyclic Cross-Correlograms (Napolitano 2009, Lemma 7.2). Under Assumptions 2.4.5 (data-tapering window regularity) and 2.6.8 (mixing conditions (IV)), for every k ≥ 2 and > 0 one obtains

(2.230)

where the order of the two limits cannot be interchanged.

Proof: See Section 3.11.

Theorem 2.6.20 Asymptotic Joint Normality of the Hybrid Cyclic Cross-Correlograms (Napolitano 2009, Theorem 7.5). Let y(t) and x(t) be zero-mean wide-sense jointly GACS stochastic processes with cross-correlation function (2.31c). Under Assumptions 2.4.2 (uniformly almost-periodic statistics), 2.4.3 (Fourier series regularity), 2.4.5 (data-tapering window regularity), and 2.4.8 (mixing conditions (I)) (with the sets and finite) and under Assumptions 2.6.8 (mixing conditions (IV)), 2.6.11 (aliasing series summability), and 2.6.15 (lack of support curve clusters (III)), and provided that γ > 1 (or γ = 1 in the special case of a(t) = rect(t)), the random variables defined in (2.229)

are asymptotically (as N→ ∞ and T_s → 0 with NT_s→ ∞) zero-mean jointly complex Normal with asymptotic covariance matrix Σ with entries

(2.231)

given by (2.227) and asymptotic conjugate covariance matrix Σ^(c) with entries

(2.232)

given by (3.260).

Proof: See Section 3.11.

Theorems 2.6.17, 2.6.18, and 2.6.20 show that the H-CCC has the same asymptotic bias, covariance and distribution of the continuous-time cyclic cross-correlogram, provided that the aliasing in the cycle-frequency domain is controlled so that there is no cluster of cycle frequencies for the ACS discrete-time process. Thus, there is no loss in asymptotic performance by carrying out discrete-time estimation instead of continuous-time estimation of the cyclic cross-correlation function.

2.6.4 Concluding Remarks

Let us assume, without loss of generality, that T (2N + 1)T_s and t₀ n₀T_s, with and . The DT-CCC approaches in the mean-square sense the continuous-time cyclic cross-correlogram as the sampling period approaches zero. Specifically, we have the following result.

Theorem 2.6.21 Asymptotic Discrete-Time Cyclic Cross-Correlogram. Let x_d(n) and y_d(n) be the discrete-time processes given by (2.172). Under Assumptions 2.4.2 (uniformly almost-periodic statistics), 2.4.3 (Fourier series regularity), 2.4.4 (fourth-order moment boundedness), and 2.4.5 (data-tapering window regularity) (assumptions of Theorem 2.4.7) on the continuous-time processes x(t) and y(t), one obtains

(2.233)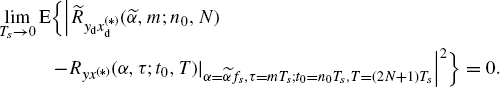

Proof: See Section 3.12.

Remark 2.6.22 In Theorems 2.6.4–2.6.21 the cycle frequencies , , and of the discrete-time ACS process are assumed to be fixed and the cycle-frequency resolution is 1/N. If a bidimensional analysis with variable cycle frequency and discrete-lag m is carried out, then should vary continuously in [− 1/2, 1/2). However, in practical implementations of bidimensional analysis, assumes values uniformly distributed in a finite set of points of [− 1/2, 1/2). Then, in order to prove mean-square consistency and asymptotic Normality, the assumption

(2.234)

should be made, where o denotes “small oh” Landau symbol, that is, as N→ ∞ means as N→ ∞.

For example, we can assume

(2.235)

with γ > 1 and denoting the floor operation. Analogously, mean-square consistency and asymptotic Normality can be proved in the case of nonuniformly sampled cycle frequencies such that

(2.236)

2.6.4.1 Subsampling-Based Estimates

In the previous sections, under mild assumptions, it is shown that the continuous-time cyclic cross-correlogram of a GACS process is asymptotically complex Normal as T→ ∞. Analogous results are found for the DT-CCC as N→ ∞ and for the H-CCC as N→ ∞ and T_s → 0 with NT_s→ ∞.

In order to perform a statistical test for presence of generalized almost cyclostationarity, covariance and conjugate covariance need to be known or estimated. If a complete knowledge of lag-dependent cycle frequencies and generalized cyclic second-and fourth-order statistics is available, then covariance and conjugate covariance can be computed, even if their expression generally involves infinite sums, and hence their value can only be approximated. If such a priori knowledge is only partial or not available, then subsampling techniques can be used in order to obtain estimates starting from a single realization of the process. For example, the subsampling technique (Politis 1998) provides the estimate

(2.237)

for the variance

(2.238)

where denotes a subsampling-based estimate of the expectation operator, b is the block size, and T = kb for some k. Convergence is obtained when b→ ∞, T→ ∞, and b/T → 0 assuming finite or practically finite memory for the processes (see (Lenart et al. 2008) for the cyclostationary case).

2.6.4.2 Estimation of Cyclic Higher-Order Statistics

In (Napolitano and Tesauro 2011), stochastic processes with higher-order statistical functions decomposable into an almost-periodic function plus a residual term not containing finite-strength additive sinewave components are considered (see (2.80a), (2.80b), (2.90a), and (2.90b)). These processes arise in mobile communications when ACS processes pass through time-varying channels. They include as special case the GACS processes.

For this class of processes, in (Napolitano and Tesauro 2011), the problem of estimating the Fourier coefficients of the (generalized) Fourier series expansion of the almost-periodic component of higher-order statistical functions of K possible distinct processes is addressed. The Kth-order cyclic cross-correlogram is proposed as an estimator of the Kth-order cyclic temporal cross-moment function. Expected value, cross-cumulants, and covariance of the cyclic cross-correlogram are derived for finite data-record length T, under mild regularity assumptions on the data-tapering window and the Fourier series convergence and under boundedness assumptions of moments and residual terms. Asymptotic (T→ ∞) expressions for expected value, cross-cumulants, and covariance, and the rate of convergence of bias of the cyclic cross-correlogram are derived under mixing conditions, residual term integrability assumption, and lack of clusters of lag-dependent cycle frequencies. Furthermore, the asymptotic (T→ ∞) joint complex Normality of cyclic correlograms at different lag vectors and cycle frequencies is proved. Thus, the Kth-order cyclic cross-correlogram is shown to be a mean-square consistent, asymptotically complex Normal estimator of the Kth-order cyclic temporal cross-moment function.

A Kth-order cyclic temporal cross-cumulant estimator is proposed as a combination of a finite number Q of products of Kth-and lower-order cyclic cross-correlograms. Asymptotic expected value and cross-cumulants of the cyclic cumulant estimator are derived and the asymptotic covariance is obtained as a special case. Moreover, the rate of convergence of bias is derived and the asymptotic joint complex Normality of estimators at different lag vectors and cycle frequencies is proved. In the limit as Q and the data-record length T approach infinity, the cyclic cross-cumulant estimator is proved to be mean-square consistent. Interestingly, it is found that the rate of decay to zero with the data-record length of the bias of the Kth-order cyclic cross-correlogram is , where |f|^−γ is the rate of decay to zero as |f|→ ∞ of the Fourier transform of the data-tapering window. In contrast, the rate of decay to zero of the bias of the cyclic cross-cumulant estimator is always . In addition, as in the almost-cyclostationary case, the cyclic cross-cumulant estimator requires the knowledge of the lower-order (moment) cycle-frequencies. Such a priori knowledge, however, is not necessary when K is the lowest-order of cyclostationarity exhibited by the process.

The proposed estimators have the same computational complexity of previously proposed estimators for ACS processes.