CHAPTER 9 Line Detection
9.1 Introduction
Straight edges are among the most common features of the modern world, arising in perhaps the majority of manufactured objects and components, not least in the very buildings in which we live. Yet it is arguable whether true straight lines ever arise in the natural state. Possibly the only example of their appearance in virgin outdoor scenes is the horizon—although even this is clearly seen from space as a circular boundary! The surface of water is essentially planar, although it is important to realize that this is a deduction. The fact remains that straight lines seldom appear in completely natural scenes. Be all this as it may, it is vital both in city pictures and in the factory to have effective means of detecting straight edges. This chapter studies available methods for locating these important features.
Historically, the Hough transform (HT) has been the main means of detecting straight edges, and over the 40 years since the method was originally invented (Hough, 1962) it has been developed and refined for this purpose. Hence, this chapter concentrates on this particular technique; it also prepares the ground for applying the HT to the detection of circles, ellipses, corners, and so on, in the next few chapters. We start by examining the original Hough scheme, even though it is now seen to be wasteful in computation, since important principles are involved.
9.2 Application of the Hough Transform to Line Detection
The basic concept involved in locating lines by the HT is point-line duality. A point P can be defined either as a pair of coordinates or in terms of the set of lines passing
through it. The concept starts to make sense if we consider a set of collinear points Pi, then list the sets of lines passing through each of them, and finally note that just one line is common to all these sets. Thus, it is possible to find the line containing all the points Pi, merely by eliminating those that are not multiple hits. Indeed, it is easy to see that if a number of noise points Qj, are intermingled with the signal points Pi, the method will be able to discriminate the collinear points from among the noise points at the same time as finding the line containing them, merely by searching for multiple hits. Thus, the method is inherently robust against noise, as indeed it is in discriminating against currently unwanted signals such as circles.
The duality goes further. For just as a point can define (or be defined by) a set of lines, so a line can define (or be defined by) a set of points, as is obvious from the above argument. This makes the above approach to line detection a mathematically elegant one, and it is perhaps surprising that the Hough detection scheme was first published as a patent (Hough, 1962) of an electronic apparatus for detecting the tracks of high-energy particles rather than as a paper in a learned journal.
The form in which the method was originally applied involves parametrizing lines by the slope-intercept equation
Every point on a straight edge is then plotted as a line in (m, c) space corresponding to all the (m, c) values consistent with its coordinates, and lines are detected in this space. The embarrassment of unlimited ranges of the (m, c) values (near-vertical lines require near-infinite values of these parameters) is overcome by using two sets of plots, the first corresponding to slopes of less than 1.0 and the second to slopes of 1.0 or more. In the latter case, equation (9.1) is replaced by the form:
The need for this rather wasteful device was removed by the Duda and Hart (1972) approach, which replaces the slope-intercept formulation with the so-called normal (6, p) form for the straight line (see Fig. 9.1):
To apply the method using this form, the set of lines passing through each point Pi, is represented as a set of sine curves in (θ, ρ) space. For example, for point P1(x1, y1) the sine curve has the equation
Then multiple hits in (θ, ρ) space indicate, via their θ, ρ values, the presence of lines in the original image.
Each of the methods described above employs an “abstract” parameter space in which multiple hits are sought. Earlier we talked about “plotting” points in parameter space, but in fact the means of looking for hits is to seek peaks that have been built by accumulation of data from various sources. Although it might be possible to search for hits by logical operations such as use of the AND function, the Hough method gains considerably by accumulating evidence for events by a voting scheme. It will be seen below that this is the source of the method’s high degree of robustness.
Although the methods described above are mathematically elegant and are capable of detecting lines (or sets of collinear points—which may be completely isolated from each other) amid considerable interfering signals and noise, they are subject to severe computational problems. The reason for this is that every prominent point1 in the original image gives rise to a great many votes in parameter space. Thus, for a 256 × 256 image the (m, c) parametrization requires 256 votes to be accumulated, while the (6, p) parametrization requires a similar number—say 360 if the 6 quantization is to be fine enough to resolve 1° changes in line orientation.
A vital key to overcoming this problem was discovered by O’Gorman and Clowes (1976), who noted that points on lines are usually not isolated but instead are joined in fragments that are sufficiently long that their directions can be measured. Supposing that direction is known with high accuracy, it is then sufficient to accumulate just one vote in parameter space for every potential line point. (If the local gradient is known with lesser accuracy, then parameter space can be quantized more coarsely—say in 10° steps (O’Gorman and Clowes, 1976)—and again a single vote per point can be accumulated.) This method is much more modest in its computational requirements and was soon adopted by other workers.
The computational load is still quite substantial, however. Not only is a large 2-D storage area needed, but this must be searched carefully for significant peaks—a tedious task if short line segments are being sought. Various means have been tried for cutting down computation further. Dudani and Luk (1978) tackled the problem by trying to separate out the 6 and p estimations. They accumulated votes first in a 1-D parameter space for 6—that is, a histogram of 6 values. (It must not be forgotten that such a histogram is itself a simple form of HT.)2 Having found suitable peaks in the 6 histogram, they then built a p histogram for all the points that contributed votes to a given 6 peak, and they repeated this for all 6 peaks. Thus, two 1-D spaces replace the original 2-D parameter space, with very significant savings in storage and load. Dudani and Luk applied their method to images of outdoor scenes containing houses. These images have the following characteristics: (1) many parallel lines, (2) many lines that are naturally broken into smaller segments (e.g., parts of a roof line broken by windows), and (3) many short-line segments. It seems that the method is particularly well adapted to such scenes, although it may not be so suitable for more general images. For example (as will also be seen with circle and ellipse detection), two-stage methods tend to be less accurate since the first stage is less selective. Biased 6 values may result from pairs of lines that would be well separated in a 2-D space. For the same reason, problems of noise tend to be more acute. In addition, any error in estimating 6 values is propagated to the p determination stage, making values of p even less accurate. (The latter problem may be reduced by searching the full (6, p) space locally around the important 6-values, although this procedure increases computation again.)
The more efficient methods outlined above require 6 to be estimated for each line fragment. Before showing how this is carried out, it is worth noting that straight lines and straight edges are different and should ultimately be detected by different means. Straight edges are probably more common than lines, true lines (such as telephone wires in outdoor scenes) being picked up by Laplacian-type operators and straight edges by edge detectors (such as the Sobel) described in Chapter 5. The two are different in that edges have a unique direction defined by that of the edge normal, whereas lines have 180° rotation symmetry and are not vectors. Hence, application of the HT to the two cases will be subtly different. For concreteness, we here concentrate on straight edge detection, although minor modification to the techniques (changing the range of 6 from 360° to 180°) permits this method to be adapted to lines.
To proceed with line detection, we first obtain the local components of intensity gradient, then deduce the magnitude g, and threshold it to locate each edge pixel in the image. The gradient magnitude g may readily be computed from the components of intensity gradient:
or using a suitable approximation (Chapter 5). 6 may be estimated using the arctan function in conjunction with the local edge gradient components gx, gy:
Since the arctan function has period π, an additional π may have to be added. This can be decided from the signs of gx and gy. Once 6 is known, ρ can be found from equation (9.4).
9.3 The Foot-of-Normal Method
Davies (1986c) has worked on an alternative means of saving computation that eliminates the use of trigonometric functions such as arctan by employing a different parametrization scheme. As noted earlier, the methods so far described all employ an abstract parameter space in which points bear no immediate relation to image space. In the author’s scheme, the parameter space is a second image space, which may be said to be congruent3 to image space. In some ways, this is highly convenient—for example, while setting up the algorithm—since working parameters and errors can be visualized and estimated more easily. Note also that it is common for there to be an additional space in the framestore which can be used for this purpose (see Chapter 2).
This type of parameter space is obtained in the following way. First, each edge fragment in the image is produced much as required previously so that ρ can be measured, but this time the foot of the normal from the origin is itself taken as a voting position in parameter space (Fig. 9.1). The foot-of-normal position embodies all the information previously carried by the ρ and θ values, and the methods are mathematically essentially equivalent. However, the details differ, as will be seen.
The detection of straight edges starts with the analysis of (1) local pixel coordinates (x, y) and (2) the corresponding local components of intensity gradient (gx, gy) for each edge pixel. Taking (x0, y0) as the foot of the normal from the origin to the relevant line (produced if necessary—see Fig. 9.2), it is found that

Figure 9.2 Image space parametrization of a straight line: (a) parameters involved in the calculation (see text); (b) buildup of foot-of-normal positions in parameter space for a more practical situation, where the line is not exactly straight: e is a typical edge fragment leading to a single vote in parameter space.
These two equations are sufficient to compute the two coordinates (x0, y0). (This must be so since the point (x0,y0) is uniquely determined as the join of the line to be detected and the normal through the origin.) Solving for x0 and y0gives
Notice that these expressions involve only additions, multiplications, and just one division.
For completeness, we also compute the distance of the line from the origin:
and the vector from (x0, y0) to the current pixel (x, y). This has components
The magnitude of this vector is
The last equation also turns out to be useful for image interpretation, as will be seen below. The next section considers the errors involved in estimating (x0, y0) from the raw data and shows how they may be minimized.
9.3.1 Error Analysis
The most serious cause of error in estimating (x0, y0) is that involved in estimating edge orientation. Pixel location is generally accurate to within 1 pixel, and even when this is not quite valid, errors are largely averaged out during peak location in parameter space. In the following we ignore errors in pixel location and concentrate on edge orientation errors. Figure 9.3 shows the geometry of the situation. A small angular error ε causes the estimate of (x0, y0) to shift to(x1, y1).
To a first approximation, the errors in estimating ρ and s are:
Thus, errors in both ρ and s due to angular error ε depend on distance from the origin. These errors are minimized overall if the origin is chosen at the center of the image.
The error ε arises from two main sources—intrinsic edge detector errors and noise. The intrinsic error of the Sobel operator is about 1 °; thus, image noise will generally be the main cause of inaccuracy. In this respect, it should be noted that many mechanical components possess edges that are straight to a very high precision and that if each pixel of the image is quantized into at least 8 bits (256 gray levels), then aliasing4 problems are minimized and the ground is laid for accurate line transforms.
Since errors in the foot-of-normal position are proportional to s and ρ, and these in turn are limited by the image size, errors may be reduced overall by dividing the image into a number of separate subimages, each with an origin located at its center. In principle, by this means errors may be reduced to arbitrarily small values. However, decomposing the picture into subimages may reduce the number of (useful) points constituting a peak in parameter space, thereby decreasing the accuracy with which that peak can be located. Sometimes the number of useful points is limited by the available data, as when lines are short in length. In such cases, the subimage method helps by reducing the clutter of noise points in parameter space, thereby improving the detection of such small segments.
The subimage method should be used to increase accuracy and reduce noise when line segments are significantly shorter than the image size. The optimum subimage size depends on the lengths of the lines being detected and the lengths of the short line segments to be detected. If a long line is broken into two or more parts by analysis in subimages, this may not be too much of a disadvantage, since all the information in each line is still available at the end of the computation, although the data from the various subimage peaks will need to be correlated in order to get a complete picture. Indeed, it can be advantageous to break down long lines into shorter ones in this way, since this procedure gives crisp output data even if the line is slightly curved and slowly changes its orientation along its length. Thus, the subimage approach permits an operator to be designed to locate lines of different lengths or moderately curved lines of different shapes.
9.3.2 Quality of the Resulting Data
Although the foot-of-normal method is mathematically similar to the (θ, ρ) method, it is unable to determine line orientation to quite the same degree of accuracy. This is because it is mapped onto a discrete image-like parameter space so that the 6 accuracy depends on the fractional accuracy in determining p—which in turn depends on the absolute magnitude of p. Hence, for small ρ the orientation of a line that is predicted from the position of the peak in parameter space will be relatively inaccurate. Indeed, if ρ happens to be zero, then no information on the orientation of the line is available in parameter space (although, as has been seen, the position of the foot-of-normal is known accurately).
The difficulty can be overcome in two ways. The first is by referring to a different origin if ρ is too small. If for each edge point three noncollinear origins are available, then it will always be possible to select a value of ρ that is greater than a lower bound. Errors are easy to compute if the subimage method is employed and the origins that are available are those of adjacent subimages. Basically, the situation is that errors in estimating line orientation should not be worse than 2/S radians (for subimages of size S), although for large S they would be limited by those (around 1°) introduced by the gradient operator.
The second and more rigorous way of obtaining accurate values of line orientation is by a two-stage method. In this case, of the original set of prominent points, the subset that contributed to a given peak in the first parameter space is isolated and made to contribute to a 6 histogram, from which line orientation may be determined accurately.
It is often possible to ignore cases of small ρ or simply to acknowledge that cases of small ρ provide little line orientation information. Although this is inelegant theoretically, the amount of redundancy of many images sometimes makes this practicable, thereby saving computation. For example, if a rectangular object is to be located, there is little chance that more than one side will have ρ close to zero (see Section 9.4). Hence, the object can be located tentatively first of all from the peaks in parameter space for which ρ is large, and the interpretation confirmed with the aid of peaks for which ρ is small or zero. Figure 9.4 confirms that this can be a useful approach. Clearly, any outstanding instances of ambiguity can still be resolved by one of the methods outlined here.

Figure 9.4 Results of image space parametrization of mechanical parts. The dot at the center of each quadrant is the origin used for computing the image space transform. The crosses are the positions of peaks in parameter space, which mark the individual straight edges (produced if necessary). For further explanation, see text.
9.3.3 Application of the Foot-of-Normal Method
The methods outlined here have been tested on real images containing various mechanical components. For objects with straight edges varying between about 20 and 80 pixels in length, it was found convenient to work with subimages of size 64 × 64.
Typical results (in this case for 128 × 128 images with 64 gray levels) are shown in Fig. 9.4 Some of the objects in these pictures are grossly overdetermined by their straight edges, so low p values are not a major problem. For those peaks where p > 10, line orientation is estimated within approximately 2°. As a result, these objects are located within 1 pixel and oriented within 1 ° by this technique, without the necessity for 6 histograms. Figures 9.4a and b contain some line segments that are not detected. This is due partly to their relatively low contrast, higher noise levels, above-average fuzziness, or short length. It is also due to the thresholds set on the initial edge detector and on the final peak detector. When these were set at lower values, additional lines were detected, but other noise peaks also became prominent in parameter space, and each of these needed to be checked in detail to confirm the presence of the corresponding line in the image. This is one aspect of a general problem that arises right through the field of image analysis.
9.4 Longitudinal Line Localization
The preceding sections have provided a variety of means for locating lines in digital images and finding their orientations. However, these methods are insensitive to where along an infinite idealized line an observed segment appears. The reason is that the fit includes only two parameters. Some advantage can be gained in that partial occlusion of a line does not prevent its detection. Indeed, if several segments of a line are visible, they can all contribute to the peak in parameter space, thereby improving sensitivity. On the other hand, for full image interpretation, it is useful to have information about the longitudinal placement of line segments.
This is achieved by a further stage of processing (which may make line finding a two- or three-stage algorithm overall). The additional stage involves finding which points contributed to each peak in the main parameter space and carrying out connectivity analysis in each case. Dudani and Luk (1978) called this process “xy-grouping.” It is not vital that the line segments should be 4- or 8-connected—just that there should be sufficient points on them so that adjacent points are within a threshold distance apart; that is, groups of points are merged if they are within the prespecified threshold distance. (Dudani and Luk took this distance as being 5 pixels.) Finally, segments shorter than a certain minimum length can be ignored as too insignificant to help with image interpretation.
The distance s in the foot-of-normal method can be employed as a suitable grouping parameter, although an alternative is to use either the x or y projection, depending on the orientation of the line (i.e., use x if |m| < 1, and y otherwise).
9.5 Final Line Fitting
Dudani and Luk (1978) found it useful to include a least-squares fitting stage to complete the analysis of the straight edges present in an image. This is carried out by taking the x, y coordinates of points on the line as input data and minimizing the sum of squares of distances from the data points to the best fit line. They added this stage in order to eliminate local edge orientation accuracy as a source of error. This motivation is generally reasonable if the highest possible accuracy is required (e.g., obtaining line orientation to significantly better than 1 °). However, many workers have criticized the use of the least-squares technique, since it tends to weight up the contribution of less accurate points—including those points that have nothing to do with the line in question but that arise from image “clutter.” This criticism is probably justified, although the least-squares technique is convenient in yielding to mathematical analysis and in this case in giving explicit equations for θ and ρ in terms of the input data (Dudani and Luk, 1978). Dudani and Luk obtained the endpoints by reference to the best fit line thus obtained.
9.6 Concluding Remarks
All the techniques for finding lines and straight edges in digital images described here are based on the HT, since the HT is virtually universally used for this purpose. The HT is very important throughout the field of image analysis, permitting certain types of global data to be extracted systematically from images and ignoring “local” problems due, for example, to occlusions and noise. The HT is therefore an example of intermediate-level processing, which may be defined as the conversion of crucial features in the image to a more abstract form that is no longer restricted to the image representation.
The specific techniques covered in this chapter have involved a particular parametrization of a straight line, as well as the means of improving efficiency and accuracy. Speed is improved particularly by resorting to a two-stage line-finding procedure—a method that is useful in other applications of the HT, as will be seen in later chapters. Accuracy tends to be reduced by such two-stage processing because of error propagation and because the first stage is subject to too many interfering signals. However, it is possible to take an approximate solution (in this case an approximation to a set of lines in an image) and to improve accuracy by including yet another stage of processing. Two examples in the chapter were adding a line orientation stage to the foot-of-normal method and adding a line-fitting procedure to refine the output of an HT procedure (although there are problems with using the least-squares technique for this purpose). Again, later chapters illustrate these types of accuracy-enhancing procedures applied in other tasks such as circle center location.
Overall, use of the HT is central to image analysis and will be encountered many times in the remainder of the book. However, it is always important to remember its limitations, especially its considerable storage and computational requirements. Further discussion of HT line finding schemes, including those aimed at saving computation, is found in Chapter 11.
The Hough transform is one way of inferring the presence of objects from their feature points. This chapter has shown how line detection may be achieved by a simple voting scheme in a carefully selected parameter space representation, starting with edge features. The transform is highly robust as it focuses only on positive evidence for the existence of objects.
9.7 Bibliographical and Historical Notes
The Hough transform (HT) was developed in 1962 (Hough, 1962) with the aim of finding (straight) particle tracks in high-energy nuclear physics, and it was brought into the mainstream image analysis literature much later by Rosenfeld (1969). Duda and Hart (1972) developed the method further and applied it to the detection of lines and curves in digital pictures. O’Gorman and Clowes (1976) soon developed a Hough-based scheme for finding lines efficiently, by making use of edge orientation information, at much the same time that Kimme et al. (1975) applied the same method (apparently independently) to the efficient location of circles. Many of the ideas for fast effective line finding described in this chapter emerged in a paper by Dudani and Luk (1978). Davies’ foot-of-normal method (1986c) was developed much later. During the 1990s, work in this area progressed further—see, for example Atiquzzaman and Akhtar’s (1994) method for the efficient determination of lines together with their end coordinates and lengths; Lutton et al.’s (1994) application of the transform to the determination of vanishing points; Marchant and Brivot’s (1995) application to the location of plant rows for tractor guidance (see also Chapter 20); and Kamat-Sadekar and Ganesan’s (1998) extensions of the technique to cover the reliable detection of multiple line segments, particularly in relation to road scene analysis. Other applications of the HT are covered in the following few chapters, while further methods for locating lines are described in Chapter 11 on the generalized HT.
Some mention should be made of the related Radon transform. It is formed by integrating the picture function I(x, y) along infinitely thin straight strips of the image, with normal coordinate parameters (6, p), and recording the results in a (6, p) parameter space. The Radon transform is a generalization of the Hough transform for line detection (Deans, 1981). For straight lines, the Radon transform reduces to the Duda and Hart (1972) form of the HT, which, as remarked earlier, involves considerable computation. For this reason the Radon transform is not covered in depth in this book. The transforms of real lines have a characteristic “butterfly” shape (a pencil of segments passing through the corresponding peak) in parameter space. This phenomenon has been investigated by Leavers and Boyce (1987), who have devised special 3 × 3 convolution filters for sensitively detecting these peaks.
A few years ago there was a body of opinion that the HT is completely worked over and no longer a worthwhile topic for research. However, this view seems misguided, and there is continuing strong interest in the subject—as the following chapters will show. After all, the computational difficulties of the method reflect a problem that is inescapable in image analysis as a whole, so development of methods must continue. In this context, note especially Sections 11.10 and 11.11.
Most recently, Schaffalitsky and Zisserman (2000) carried out an interesting extension of earlier ideas on vanishing lines and points by considering the case of repeated lines such as those that occur on certain types of fences and brick buildings. Song et al. (2002) developed HT methods for coping with the problems of fuzzy edges and noise in large-sized images; Davies (2003b) explored how the size of the parameter space could usefully be minimized; and Guru et al. (2004) demonstrated that there are viable alternatives to the Hough transform, based, for example, on heuristic search achieved by small eigenvalue analysis.
9.8 Problems
1. (a) In the foot-of-normal Hough transform, straight edges are found by locating the foot-of-the-normal F (xf, yf) from an origin O (0, 0) at the center of the image to an extended line containing each edge fragment E (x, y), and placing a vote at F in a separate image space.
(b) By examining the possible positions of lines within a square image and the resulting foot-of-normal positions, determine the exact extent of the parameter space that is theoretically required to form the Hough transform.
(c) Would this form of the Hough transform be expected to be (i) more or less robust and (ii) more or less computation intensive than the (p, 6) Hough transform for line location?
2. (a) Why is it sometimes stated that a Hough transform generates hypotheses rather than actual solutions for object location? Is this statement justified?
(b) A new type of Hough transform is to be devised for detecting straight lines. It will take every edge fragment in the image and extend it in either direction until it meets the boundary of the image, and then it will accumulate a vote at each position. Thus, two peaks should result for every line. Explain why finding these peaks will require less computation than for the standard Hough transform, but that deducing the presence of lines will then require extra computation. How will these amounts of computation be likely to vary with (i) the size of the image, and (ii) the number of lines in the image?
(c) Discuss whether this approach would be an improvement on the standard approach for straight-line location and whether it would have any disadvantages.
3. (a) Describe the Hough transform approach to object location. Explain its advantages relative to the centroidal (r, 6) plot approach: illustrate your answer with reference to the location of circles of known radius R.
(b) Describe how the Hough transform may be used to locate straight edges. Explain what is seen in the parameter space if many curved edges also appear in the original image.
(c) Explain what happens if the image contains a square object of arbitrary size and nothing else. How would you deduce from the information in parameter space that a square object is present in the image? Give the main features of an algorithm to decide that a square object is present and to locate it.
(d) Examine in detail whether an algorithm using the strategy described in (c) would become confused if (i) parts of some sides of the square were occluded; (ii) one or more sides of the square were missing; (iii) several squares appeared in the image; (iv) several of these complications occurred together.
(e) How important is it to this type of algorithm to have edge detectors that are capable of accurately determining edge orientation? Describe a type of edge detector that is capable of determining orientation accurately.
1 For the present purpose it does not matter in what way these points are prominent. They may in fact be edge points, dark specks, centers of holes, and so on. Later we shall consistently take them to be edge points.
2 It is now common for any process to be called an HT if it involves accumulating votes in a parameter space, with the intention of searching for significant peaks to find properties of the original data.
3 That is, parameter space is like image space, and each point in parameter space holds information that is immediately relevant to the corresponding point in image space.
4 Aliasing is the process whereby straight lines in digital images take a stepped form following sampling decisions that they pass through one pixel but not the next one. The process is often marked in graphics (binary) images and is less marked, though never absent, in gray-scale images. See also Chapter 27.


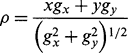 (9.13)
(9.13) (9.17)
(9.17)