Example 1.15
Assume that 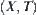 is a semi-order set as shown in Fig. 1.5. Let
is a semi-order set as shown in Fig. 1.5. Let 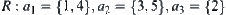 . From Example 1.14, we have that
. From Example 1.14, we have that 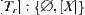 is a topology on [X] corresponding to R, i.e.,
is a topology on [X] corresponding to R, i.e., 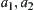 and
and 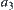 have the same neighborhood system on [X]. Based on the mergence method, we have a revised partition
have the same neighborhood system on [X]. Based on the mergence method, we have a revised partition 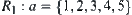 . The example shows that undoubtedly by the mergence method, an incompatible equivalence relation can be transformed into a compatible and the finest one. But in some cases, the revised grain-size is too coarse. In the example,
. The example shows that undoubtedly by the mergence method, an incompatible equivalence relation can be transformed into a compatible and the finest one. But in some cases, the revised grain-size is too coarse. In the example, 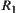 only has one equivalence class, this is an extreme case. This is not our expectation.
only has one equivalence class, this is an extreme case. This is not our expectation.
In order to overcome the shortage of the mergence method, the space [X] may be refined such that the revised equivalence relation 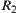 is compatible. Of course, such
is compatible. Of course, such 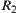 exists, since X itself has already satisfied the compatible requirement, but it is too fine. So the point is to find the coarsest one among all refined spaces, i.e., the refinement method has minimality. This is the decomposition method that we will discuss below.
exists, since X itself has already satisfied the compatible requirement, but it is too fine. So the point is to find the coarsest one among all refined spaces, i.e., the refinement method has minimality. This is the decomposition method that we will discuss below.
1.6.2. Decomposition Methods
In the following discussion, we assume that 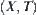 is a finite semi-order set, its topology is a right-order topology of T.
is a finite semi-order set, its topology is a right-order topology of T. 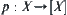 is a projection, where [X] is a quotient space.
is a projection, where [X] is a quotient space.
Definition 1.25
Definition 1.26
Assume that 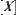 is a quotient space of
is a quotient space of 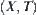 , R is its corresponding equivalence relation. From Section 1.5, we have
, R is its corresponding equivalence relation. From Section 1.5, we have 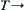 right-order topology
right-order topology 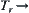 quotient topology
quotient topology 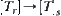 .
. 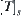 is called a pseudo semi-order on
is called a pseudo semi-order on 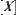 . When R is compatible,
. When R is compatible, 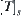 is a semi-order. If
is a semi-order. If 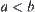 on
on 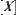 under the topology
under the topology 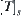 , where
, where 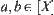 , then it is denoted as
, then it is denoted as 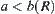 .
.
Definition 1.27
R is an equivalence relation on 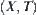 and its corresponding quotient space is [X]. For
and its corresponding quotient space is [X]. For 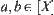 , if
, if 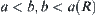 , then a and b are pseudo-equivalent and denoted by
, then a and b are pseudo-equivalent and denoted by 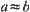 .
.
Definition 1.28
If [X] is a quotient spare corresponding to R, for 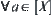 letting
letting 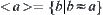 ,
, 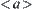 is called a pseudo-equivalence class corresponding to a.
is called a pseudo-equivalence class corresponding to a.
Lemma 1.4
If A is a pseudo-equivalence class on [X], then 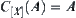 , or simply C(A) if it does not cause any confusion.
, or simply C(A) if it does not cause any confusion.
Proof:
Otherwise, 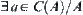 . From
. From 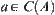 and the definition of C(A), we can see that
and the definition of C(A), we can see that 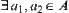 such that
such that 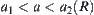 . Since
. Since 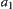 and
and 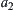 are pseudo-equivalent
are pseudo-equivalent 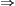
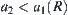 . We have
. We have 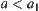 , then,
, then,  and
and 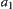 are pseudo-equivalent, i.e.,
are pseudo-equivalent, i.e., 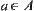 . This is in contradiction to
. This is in contradiction to  .
.
Lemma 1.5
Let 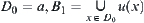 , where
, where 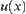 on
on 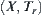 is a minimal open set containing x.
is a minimal open set containing x. 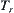 is a right-order topology of T.
is a right-order topology of T.
Let 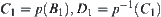 ,
, 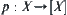 is a projection.
is a projection.
Generally, we define 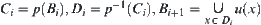 .
.
Since 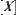 is finite, there exists a minimal integer n such that
is finite, there exists a minimal integer n such that 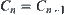 .
.
Let 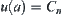 . Set
. Set 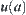 is just a minimal open set on
is just a minimal open set on 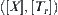 containing a.
containing a.
Proof:
First, we show that 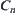 is an open set.
is an open set.
![]()
Since  , have
, have 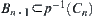 . Thus,
. Thus, 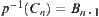 .
.
Since 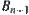 is an open set,
is an open set, 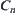 is open.
is open.
Assuming that 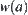 is an arbitrary open set containing a, then
is an arbitrary open set containing a, then 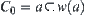 .
.
By induction, assume that 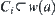 .
.
From the continuity of p, 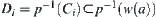 .
.
From induction, we have  . Therefore
. Therefore 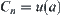 is a minimal open set containing a.
is a minimal open set containing a.
Lemma 1.6
R is an equivalence relation in semi-order space 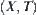 . Let
. Let 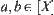
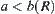 , there exist
, there exist 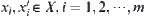 such that
such that 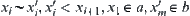 .
.
Proof:
Letting 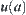 be a minimal open set containing a, since
be a minimal open set containing a, since 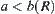 , have
, have 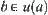 .
.
From Lemma 1.5, we have 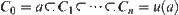 .
.
Assuming that 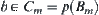 , we have
, we have 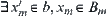 , i.e.,
, i.e., 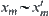 .
.
Since 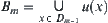 , have
, have 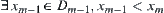 .
.
Moreover, 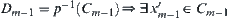 such that
such that 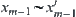 .
.
By induction, for 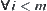 , have
, have 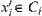 ,
, 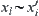 and
and  ,
, 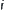 = 1, 2,…,
= 1, 2,…,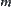 .
.
Namely, 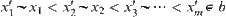 .
.
We will prove Proposition 1.10 by using Lemma 1.6 below.
Proposition 1.10
Assume that 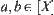 , then
, then 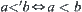 , where
, where  is a pseudo semi-order on quotient space
is a pseudo semi-order on quotient space 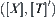 .
.
Proof:
Assume that 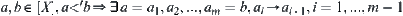 ,
, 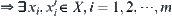 , have
, have 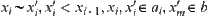 .
.
Letting 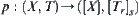 be a natural projection, from the order-preserving ability of p, have
be a natural projection, from the order-preserving ability of p, have 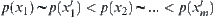
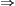
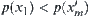
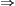
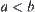 .
.
Conversely, assume 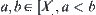 . From Lemma 1.6,
. From Lemma 1.6, 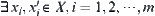 , such that
, such that 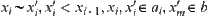
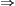
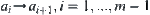 . From the definition of ‘
. From the definition of ‘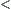 ’, we have
’, we have 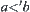 .
.
Decomposition Method
When R and T are not compatible, we will show below how to decompose R such that the decomposed R′ is compatible with T.
(1) If 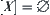 , then stop and A is what we want. Otherwise, go to (2).
, then stop and A is what we want. Otherwise, go to (2).
(2) For 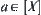 , let
, let  . If
. If 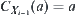 , letting
, letting 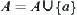 and
and 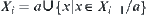 , then
, then  and
and 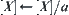 , go to (1). Otherwise, go to (3).
, go to (1). Otherwise, go to (3).
(3) Decomposing a, have  . Let
. Let 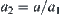 .
.
(3.1) If  , we have the decomposition
, we have the decomposition 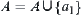 . Letting
. Letting 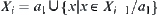 , then
, then
(3.2) If 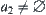 , letting
, letting 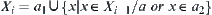 and
and 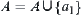 , then
, then  and
and  , go to (3).
, go to (3).
Finally, we have a space denoted as  . Its corresponding equivalence relation is
. Its corresponding equivalence relation is 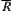 .
. 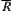 is what we want.
is what we want.  is called a normed decomposition space of [X]. We will prove below that
is called a normed decomposition space of [X]. We will prove below that 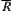 is compatible with X and has minimality.
is compatible with X and has minimality.
Before the proof of the above basic property, we will show some properties of semi-order closures.
Definition 1.29
The properties of  are as follows.
are as follows.
Property 1.2
Proof:
Assuming 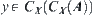 , there exist
, there exist  and
and 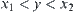 , i.e.,
, i.e., 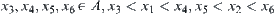 . We have
. We have 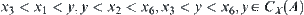 . Thus,
. Thus,  is semi-order closed.
is semi-order closed.
Property 1.3
Proof:
Assuming  , have
, have 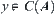 .
. 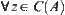 and
and  , have
, have  . From
. From  , have
, have 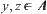 . And from the definition of boundary points, have
. And from the definition of boundary points, have 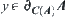 , i.e.,
, i.e., 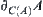 is semi-order closed.
is semi-order closed.
Property 1.4
If A is semi-order closed with respect to X, then  .
.
Proof:
Obviously, 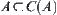 .
.
Assuming  , there exists
, there exists  . Since A is semi-order closed,
. Since A is semi-order closed, 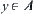 and
and 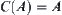 . From the definition of
. From the definition of 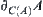 , have
, have 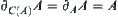 .
.
Proposition 1.11
Proof:
Assume 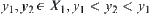 . If
. If 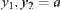 , have
, have  on
on 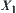 . If
. If 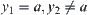 , from Lemma 1.5, have
, from Lemma 1.5, have 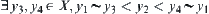 . From a is semi-order closed, have
. From a is semi-order closed, have 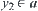 . This is a contradiction.
. This is a contradiction.
If  , from Lemma 1.5, have
, from Lemma 1.5, have 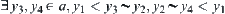 . Thus,
. Thus, 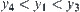 and
and 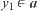 . This is a contradiction.
. This is a contradiction.
We have that 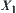 is a semi-order space.
is a semi-order space.
Theorem 1.7
Proof:
Let 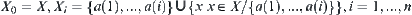 . From Property 1.3, each
. From Property 1.3, each 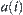 is semi-order closed on
is semi-order closed on 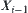 . From Proposition 1.10, we have that
. From Proposition 1.10, we have that 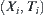 is a semi-order space. Letting
is a semi-order space. Letting  , have
, have  . Namely, quotient space
. Namely, quotient space 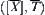 is a semi-order one.
is a semi-order one.
Lemma 1.7
Proof:
First, we prove that 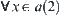 ,
,  and
and  such that
such that 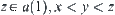 . From the definition of
. From the definition of 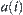 ,
,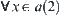 there must exist
there must exist 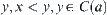 , but
, but  . Otherwise, from the definition of
. Otherwise, from the definition of 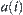 ,
, 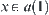 . This is a contradiction. And from
. This is a contradiction. And from 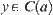 , we have
, we have  and
and  . Then,
. Then, 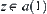 . Otherwise,
. Otherwise, 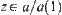 . This is in contradiction with
. This is in contradiction with 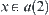 . From the definition of quotient structures, we have
. From the definition of quotient structures, we have 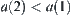 .
.
Similarly, for 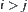 , we have
, we have 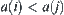 .
.
Theorem 1.8
R is an equivalence relation on semi-order set 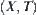 .
. 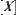 is a quotient space. Let
is a quotient space. Let 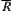 be an equivalence relation corresponding to the normed decomposition space of
be an equivalence relation corresponding to the normed decomposition space of 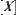 . We have
. We have
(1) 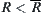 and
and 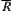 are compatible.
are compatible.
(2) 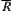 has minimality, i.e., for
has minimality, i.e., for 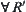 , if
, if  and
and  are compatible, then
are compatible, then 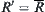 .
.
Proof:
From the procedure of the normed decomposition and Theorem 1.7, 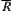 is compatible. Now, we prove that
is compatible. Now, we prove that 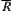 is the minimum.
is the minimum.
Assume that 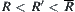 and
and  are compatible. If
are compatible. If 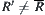 , obviously, for
, obviously, for 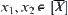 ,
,  and
and 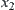 belong to the same equivalence class on
belong to the same equivalence class on 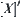 but are not equivalent on
but are not equivalent on  . Since
. Since  and
and 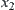 are equivalent on
are equivalent on 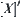 and
and 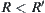 , then
, then  and
and 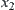 are also equivalent on R.
are also equivalent on R.
Assume that 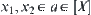 denoted
denoted 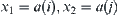 , where
, where 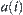 and
and  ,
, 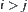 , are obtained from the normed decomposition of a. From Lemma 1.7, there exists
, are obtained from the normed decomposition of a. From Lemma 1.7, there exists 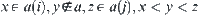 . Now we regard
. Now we regard 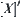 as a quotient space of X. Let
as a quotient space of X. Let 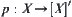 .
.
From the compatibility of  , we have p(x)<p(y)<p(z). Thus,
, we have p(x)<p(y)<p(z). Thus, 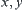 and
and  belong to the same equivalence class of
belong to the same equivalence class of 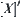 denoted by b. Then,
denoted by b. Then,  .
.
Since 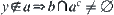 , where
, where 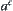 is the complement set of a, this contradicts with
is the complement set of a, this contradicts with 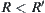 .
.
Thus,  , this is in contradiction with the assumption that
, this is in contradiction with the assumption that  and
and 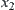 are not equivalent in
are not equivalent in  .
.
Finally, 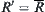 .
.
Example 1.11
For  , since
, since 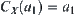 , we have
, we have  . Let
. Let 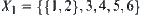 .
.
For 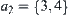 , since
, since 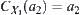 , we have
, we have 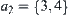 . Let
. Let 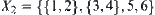 .
.
For  , since
, since 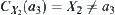 , we have
, we have  . Then
. Then 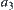 is decomposed into
is decomposed into  and
and  .
.
We have 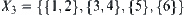 .
.  is a semi-order space. Its corresponding equivalence relation
is a semi-order space. Its corresponding equivalence relation 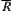 is the decomposed one of R and compatible.
is the decomposed one of R and compatible.
The decomposition procedure is shown in Fig. 1.6.
Now, we have the necessary and sufficient condition for the compatible equivalence relation R as follows.
Theorem 1.9
R is an equivalence relation corresponding to semi-order set  .
.  is its corresponding quotient space.
is its corresponding quotient space.  is a (pseudo) semi-order closure of a on
is a (pseudo) semi-order closure of a on 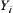 . Then, R and T are compatible
. Then, R and T are compatible 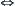
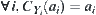 .
.
Proof:
Obviously, if 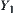 is a quotient space of Y, then
is a quotient space of Y, then 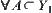 ,
, 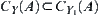 .
.
1.6.3. The Existence and Uniqueness of Quotient Semi-Order
Assume that 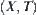 is a semi-order space. From the previous discussion, we have the following results.
is a semi-order space. From the previous discussion, we have the following results.
1. If equivalence relation R and semi-order structure T on X are compatible, we offer a method that induces a quotient semi-order of [X] such that its projection has the order-preserving ability.
2. If equivalence relation R and semi-order structure T on X are incompatible, we show there are modification methods such that the modified R is compatible.
(1) By mergence method, we have an equivalence relation 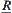 and satisfies
and satisfies
(a)  , (b)
, (b) 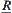 is compatible, and (c)
is compatible, and (c) 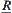 is the maximum (finest).
is the maximum (finest).
(2) By decomposition method, we have an equivalence relation 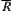 and satisfies
and satisfies
(a) 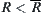 , (b)
, (b) 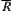 is compatible, and (c)
is compatible, and (c) 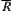 is the minimum.
is the minimum.
Therefore, under the maximal (minimal) sense, the modification above is unique.
The idea of the construction of quotient semi-order that we offered is the following.
First, a right-order topology 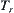 is induced from T. From
is induced from T. From 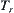 , a quotient topology
, a quotient topology 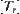 on
on 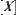 is induced. Finally, from
is induced. Finally, from 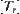 , a quotient (pseudo) semi-order on [X] is induced. Now, the point is whether there exists another method for inducing quotient semi-order. If the method exists, the induced quotient semi-order is as the former, i.e., the uniqueness of quotient semi-order. Moreover, when R and T are incompatible, we show that the method above cannot induce quotient semi-order on [X]. Then, whether there is another method that can induce quotient semi-order on [X] such that its projection is order-preserving. That is, the existence of quotient semi-order.
, a quotient (pseudo) semi-order on [X] is induced. Now, the point is whether there exists another method for inducing quotient semi-order. If the method exists, the induced quotient semi-order is as the former, i.e., the uniqueness of quotient semi-order. Moreover, when R and T are incompatible, we show that the method above cannot induce quotient semi-order on [X]. Then, whether there is another method that can induce quotient semi-order on [X] such that its projection is order-preserving. That is, the existence of quotient semi-order.
The following two propositions answer the above uniqueness and existence problems.
Proposition 1.12
R is an equivalence relation on semi-order set 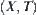 . R and T are compatible. Let [T] be the quotient semi-order obtained from the above method.
. R and T are compatible. Let [T] be the quotient semi-order obtained from the above method. 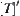 is any quotient semi-order that has the order-preserving projection
is any quotient semi-order that has the order-preserving projection 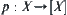 , then
, then  .
.
Proof:
Assuming 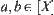 , then
, then 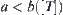 . From Lemma 1.5, we have
. From Lemma 1.5, we have
![]()
Let  . From the assumption that p is order-preserving, have
. From the assumption that p is order-preserving, have 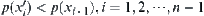 and
and 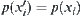 .
.
Thus,  , i.e., there exists
, i.e., there exists 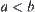 on
on 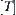
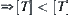 .
.
Proposition 1.13
If R and T are incompatible, there is no quotient semi-order such that 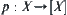 is order-preserving.
is order-preserving.
Proof:
Assume that R and T are incompatible and there exists a quotient semi-order on [X] that has the order-preserving ability. Since the incompatibility of R and T, 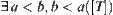 ,
,  does not hold. From
does not hold. From 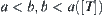 ,
, 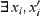 satisfy
satisfy  and
and 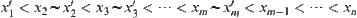 .
.
From the order-preserving ability of 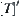 , we have
, we have  and
and  . Thus,
. Thus, 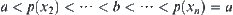 .
.
Since 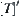 is semi-order,
is semi-order, 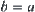 . This is in contradiction with that
. This is in contradiction with that 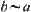 does not hold.
does not hold.
1.6.4. The Geometrical Interpretation of Mergence and Decomposition Methods
The structure of a finite semi-order space may be represented by a directed acyclic graph geometrically. For a semi-order space 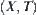 , when the quotient structure [T] of its quotient space
, when the quotient structure [T] of its quotient space 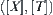 is represented by a directed graph, if there is no directed loop in the graph, then the corresponding structure is semi-order; otherwise, it is not semi-order. There are two methods to ‘remove’ the loops on the graph. One is to merge all notes on a loop into a new note and carry on until the graph becomes an acyclic one. Then the quotient structure obtained is a semi-order structure. This is the mergence method. The other one is to choose an arbitrary note on a loop and cut the loop open from the note, carry on until the graph becomes an acyclic one. This is just the idea of decomposition. Due to the different cutting sequences, the acyclic graph obtained may be different. So the semi-order structure obtained by the decomposition method is not unique. We can prove the structure is local minimum but not a global one.
is represented by a directed graph, if there is no directed loop in the graph, then the corresponding structure is semi-order; otherwise, it is not semi-order. There are two methods to ‘remove’ the loops on the graph. One is to merge all notes on a loop into a new note and carry on until the graph becomes an acyclic one. Then the quotient structure obtained is a semi-order structure. This is the mergence method. The other one is to choose an arbitrary note on a loop and cut the loop open from the note, carry on until the graph becomes an acyclic one. This is just the idea of decomposition. Due to the different cutting sequences, the acyclic graph obtained may be different. So the semi-order structure obtained by the decomposition method is not unique. We can prove the structure is local minimum but not a global one.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
