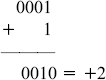3
Number Representation
![]() Unsigned binary integers
Unsigned binary integers
![]() Signed binary integers
Signed binary integers
![]() Sign Magnitude notation
Sign Magnitude notation
![]() 1's complement notation
1's complement notation
![]() 2's complement notation
2's complement notation
![]() Representation of fractions
Representation of fractions
![]() 2's complement fractions
2's complement fractions
![]() Signed floating point numbers
Signed floating point numbers
![]() Questions
Questions
A computer is quite often used for performing computations on numbers. The types of numbers on which the computer is required to perform calculations are: unsigned integers; signed integers; and signed floating point numbers.
In a digital computer everything, whether it is some data, result, or an instruction, has to be represented using only 0s and 1s. This is because the digital computer basically uses transistors that are made to work in the ‘Off’ state or the ‘On’ state. The ‘Off’ state is generally represented as the 0 state and the ‘On’ state is represented as 1 state. In computers 0s and 1s are called ‘bits’. A bit stands for ‘BInary digiT’.
 3.1 UNSIGNED BINARY INTEGERS
3.1 UNSIGNED BINARY INTEGERS
Unsigned binary integers are numbers without any ‘+’ or ‘-’ sign. Examples are: number of books in a library, runs scored by a batsman in a cricket match, etc. Obviously they are unsigned integers like 34,567 and 87. These numbers have to be represented in a computer using only binary notation or bits. Numbers are represented in a computer using a fixed size, like 4, 8, 16, 32 bits, etc. If numbers are represented in a computer using 8 bits, it is said that the computer uses 8-bit word size. Generally, word sizes are a power of 2. In the early days of computing, word sizes were generally 4 bits. These days, it is generally 32 bits or 64 bits. A tabular column of decimal numbers and their equivalent in unsigned binary is shown in the following, assuming a word size of 4 bits.
| Number | Unsigned binary notation |
| 5 | 0101 |
| 13 | 1101 |
| 0 | 0000 Minimum number, which is 0 |
| 15 | 1111 Maximum number, which is (24 - 1) |
In this table, just as 13 in decimal notation is 1 × 101 + 3 × 100, 1101 in binary is 1 × 23 + 1 × 22 + 0 × 21 + 1 × 20. From this, it is obvious that if the word size is n bits, the range of (2n – 1) numbers that can be represented is from 0 to (2n – 1). A table of word size and the range of unsigned integers that can be represented is shown here.
| Word size | Range for unsigned numbers |
| 4 | 0 to 15 |
| 8 | 0 to 255 |
| 16 | 0 to 65535 |
| 32 | 0 to 4,294,967,295 |
In other words, when the word size is only 4 bits, it is not possible to represent a number like 223. The minimum word size has to be 8 bits to represent the number 223.
 3.2 SIGNED BINARY INTEGERS
3.2 SIGNED BINARY INTEGERS
Signed integers are numbers with a ‘+’ or ‘-’ sign. An example is the list of temperatures (correct to nearest digit) in various cities of the world. Obviously they are signed integers like +34, -15, -23, and +17. These numbers along with their sign have to be represented in a computer using only binary notation or bits.
There are various ways of representing signed numbers in a computer. The simplest way of representing a signed number is the sign magnitude (SM) method.
3.2.1 SIGN MAGNITUDE NOTATION
In this method of representing signed numbers, the most significant bit (MSB) indicates the sign of the number. The number is treated as positive, if the MSB is 0. It is negative if the MSB is 1. The other bits indicate the magnitude of the number.
A tabular column of signed decimal numbers and their equivalent in SM notation follows assuming a word size of 4 bits.
| Number | SM notation |
| +5 0 | 101 |
| -5 | 1 101 |
| +3 | 0 011 |
| -3 | 1 011 |
| +7 | 0 111 Most positive number, which is +(23 - 1) |
| +0 | 0 000 Notation for +0 |
| -0 | 1 000 Notation for -0 |
| -7 | 1 111 Most negative number, which is -(23 - 1) |
From this table, it is obvious that if the word size is n bits, the range of numbers that can be represented is from -(2n-1 - 1) to +(2n-1 - 1). A table of word size and the range of SM numbers that can be represented is shown in the following.
| Word size | Range for SM numbers |
| 4 | -7 to +7 |
| 8 | -127 to +127 |
| 16 | -32767 to +32767 |
| 32 | -2147483647 to +2147483647 |
In other words, when the word size is only 4 bits, it is not possible to represent a number like –123. The minimum word size has to be 8 bits to represent the number –123.
Notice that the bit sequence 1101 corresponds to the unsigned number 13, as well as the number –5 in SM notation. Its value depends only on the way the user or the programmer interprets the bit sequence.
A number is represented inside a computer with the purpose of performing some calculation using that number. The most basic arithmetic operation in a computer is the addition operation. The following examples show the result of adding two signed numbers that are represented inside the computer in SM notation.
Example 1: Add the numbers (+5) and (-3) using a computer. The numbers are assumed to be represented using 4-bit SM notation.

The computer instead of giving the correct answer of +2 = 0010, has given the wrong answer of +0 = 0000! To give the correct answer the computer will have to manipulate the result of addition quite a lot.
Example 2: Add the numbers (-4) and (+2) using a computer. The numbers are assumed to be represented using 4-bit SM notation.

The computer instead of giving the correct answer of -2 = 1010, has given the wrong answer of -6 = 1110! To give the correct answer the computer will have to manipulate the result of addition quite a lot.
Thus to conclude: SM notation is very simple to understand because it is very similar to the conventional way of representing signed numbers. But its disadvantages are:
- There are two notations for 0 (0000 and 1000), which is very inconvenient when the computer wants to test for a 0 result.
- It is not convenient for the computer to perform arithmetic.
Hence, SM notation is generally not used to represent signed numbers inside a computer.
3.2.2 1's COMPLEMENT NOTATION
This is another method of representing signed integers in a computer. In this method also, the MSB indicates the sign of the number. The number is treated as positive, if the MSB is 0. It is negative if the MSB is 1. However, the other bits directly indicate the magnitude of the number only when the number is positive. If the number is negative, the other bits signify the 1's complement of the magnitude of the number.
A tabular column of signed decimal numbers and their equivalent in 1's complement notation is shown below, assuming a word size of 4bits.
| Number | 1's complement notation |
| +5 | 0 101 |
| -5 | 1 010 |
| +3 | 0 011 |
| -3 | 1 100 |
| +7 | 0 111 Most positive number, which is +(23-1) |
| +0 | 0 000 Notation for +0 |
| -0 | 1 111 Notation for -0 |
| -7 | 1 000 Most negative number, which is-(23 - 1) |
From the given table, it is obvious that if the word size is n bits, the range of numbers that can be represented is from -(2n-1- 1) to +(2n-1 - 1). A table of word size and the range of 1's complement numbers that can be represented is shown.
| Word size | Range for 1's complement numbers |
| 4 | -7 to +7 |
| 8 | -127 to +127 |
| 16 | -32767 to +32767 |
| 32 | -2147483647 to +2147483647 |
In other words, when the word size is only 4 bits, it is not possible to represent a number like -123. The minimum word size has to be 8 bits to represent the number -123.
Notice that the bit sequence 1101 corresponds to the following values in different notations.
- — 1101 is 13 in unsigned notation,
- — 1101 is -5 in SM notation,
- — 1101 is -2 in 1's complement notation.
Its value depends only on the way the user or the programmer interprets the bit sequence. Examples for addition of two signed numbers represented using 1's complement notation are shown below.
Example 1: Add the numbers (+5) and (-3) using a computer. The numbers are assumed to be represented using 4-bit 1's complement notation.

The computer instead of giving the correct answer of +2 = 0010, has given the wrong answer of +1 = 0001! However, to get the correct answer the computer will have to simply add to the result the final carry that is generated, as shown in the following.
Example 2: Add the numbers (-4) and (+2) using a computer. The numbers are assumed to be represented using 4-bit 1's complement notation.

After the addition of the final carry, the result remains as 1101. This is -2, which is the correct answer. If it is not clear, as to how 1101 is -2, the following explanation should make it clear. In 1 101 the MSB is a 1. It means the number is negative. Then, the remaining bits do not provide the magnitude directly. To solve this problem, just consider 1's complement of 1 101. 1's complement of 1 101 is 0 010, which is +2. Thus, 1 101, which is 1's complement of 0 010 is −2.
Thus to conclude: 1's complement notation is not very simple to understand because it is very much different from the conventional way of representing signed numbers. The other disadvantage is that there are two notations for 0 (0000 and 1111), which is very inconvenient when the computer wants to test for a 0 result.
But, it is quite convenient for the computer to perform arithmetic. To get the correct answer after addition, the result of addition and final carry has to be added up.
Hence, 1's complement notation is also generally not used to represent signed numbers inside a computer.
3.2.3 2'S COMPLEMENT NOTATION
This is yet another method of representing signed integers in a computer. In this method also, the MSB indicates the sign of the number. The number is treated as positive, if the MSB is 0. It is negative if the MSB is 1. However, the other bits directly indicate the magnitude of the number only when the number is positive. If the number is negative, the other bits signify the 2's complement of the magnitude of the number.
Thus a positive number has the same representation in SM, 1's complement, and 2's complement notations. Only negative numbers are represented differently in these notations.
| Number | 2s complement notation |
| +5 | 0 101 |
| -5 | 1 011 |
| +3 | 0 011 |
| -3 | 1 101 |
| +7 | 0 111 Most positive number, which is +(23 - 1) |
| 0 | 0 000 Notation for 0 |
| -7 | 1 001 |
| -8 | 1 000 Most negative number, which is -23 |
A tabular column of signed decimal numbers and their equivalent in 2's complement notation is shown below, assuming a word size of 4 bits.
Notice that there is a single notation for 0, immaterial of whether it is +0 or –0. One may feel that 0 000 is +0 only, as the MSB in this case is a 0. But then, the notation for –0 should be the 2's complement of 0 000, which is 1111 + 1 = 0 000 ignoring the carry.
If it is not clear, as to how 1000 is –8, the following explanation should make it clear. In 1 000 the MSB is a 1. It means the number is negative. Then, the remaining bits do not provide the magnitude directly. To solve this problem, just consider 2's complement of 1 000. 2's complement of 1 000 is 0 111 + 1 = 7 + 1 = +8. Thus, 1 000 is –8.
An alternative way of arriving at the same conclusion is as follows. Shown in the following discussion is the 2's complement notations for +5, +6, +7 and −5, −6, −7. Then a question mark is placed to indicate the value of 1 000. Using the rules of mathematical induction, 1 000 can be interpreted as either +8 or -8. However, +8 is not correct, as the MSB is 1. Thus, 1 000 has the value −8 in 2's complement notation.

Thus, in 2's complement notation an extra negative number can be represented compared with SM or 1's complement notation. This is because, in 2's complement notation, there is only a single notation for zero, whereas in SM and 1's complement notations there are two notations for 0.
From this, it is obvious that if the word size is n bits, the range of numbers that can be represented is from -2n-1 to +(2n-1 - 1). A table of word size and the range of 2's complement numbers that can be represented is shown next.
| Word size | Range for 2s complement numbers |
| 4 | -8 to +7 |
| 8 | -128 to +127 |
| 16 | -32768 to +32767 |
| 32 | -2147483648 to +2147483647 ±2 × 10+9 (approx.) |
In other words, when the word size is only 4 bits, it is not possible to represent a number like -123. The minimum word size has to be 8 bits to represent the number -123.
Notice that the bit sequence 1101 corresponds to the following values in different notations.
- — 1101 is 13 in unsigned numbers
- — 1101 is -5 in SM notation
- — 1101 is -2 in 1's complement notation
- — 1101 is -3 in 2's complement notation
Its value depends only on the way the user or the programmer interprets the bit sequence. Examples for addition of two signed numbers represented using 2's complement notation are shown next.
Example 1: Add the numbers (+5) and (-3) using a computer. The numbers are assumed to be represented using 4-bit 2's complement notation.

Notice that the computer straightaway gives the correct answer of +2 = 0010.
Example 2: Add the numbers (-4) and (+2) using a computer. The numbers are assumed to be represented using 4-bit 2's complement notation.

This is -2, which is the correct answer. If it is not clear, as to how 1110 is -2, the following explanation should make it clear. In 1 110 the MSB is a 1. It means the number is negative. Then, the remaining bits do not provide the magnitude directly. To solve this problem, just consider 2's complement of 1 110. 2's complement of 1 110 is 0 001 + 1 = 0 010, which is +2. Thus, 1 110, which is 2's complement of 0 010 is -2.
Thus to conclude: 2's complement notation is not very simple to understand because it is very much different from the conventional way of representing signed numbers.
But, its advantage is that there is a single notation for zero, which is very convenient when the computer wants to test for a 0 result. Also, it is very convenient for the computer to perform arithmetic. The addition operation straightaway gives the correct result.
Hence, 2's complement notation is generally used to represent signed numbers inside a computer.
 3.3 REPRESENTATION OF FRACTIONS
3.3 REPRESENTATION OF FRACTIONS
It may be necessary quite often to represent fractions. For example, it may be needed to represent inside a computer a value like +0.875 or -0.875. This topic is discussed next.
Let us say we have the 4-bit number 1001. Then, what is its value? It has the value 9, -1, -6, or -7 depending on whether it is unsigned, SM number, 1's complement number, or 2's complement number, respectively. Thus the value a given sequence of bits will have depends purely on the interpretation of the user.
So far, only integers were discussed. Thus, a number like 1000 was assumed to have the binary point at the extreme right of the bit sequence. To represent signed fractions, it is necessary to assume the binary point just after the MSB in the bit sequence.
The MS bit specifies the sign of a number. But then, how to specify the binary point inside a computer? This problem is easily solved if all numbers are required to have the binary point at the same position in the bit sequence. For example, if all numbers are required to have the binary point just after the MS bit, it is just assumed that it exists there! Such numbers where the binary point is assumed to be at a fixed position in the bit sequence are called fixed-point numbers.
Just as there are unsigned, SM, 1's complement, and 2's complement integers, there are also unsigned, SM, 1's complement, and 2's complement fractions. Unsigned fractions will have the assumed binary point at the extreme left. SM, 1's complement, and 2's complement fractions will have this imaginary binary point just to the right of the MS bit.
If the imaginary point is at the extreme right, then the number is an integer. If the imaginary binary point is at the extreme left for an unsigned number, the number is an unsigned fraction. If the binary point is to the immediate right of the MS bit, the number is a signed fraction. If the binary point is in the middle of a bit sequence, the number has an integer and a fractional part.
Only 2's complement fractions, which are the most common, are discussed next.
3.3.1 2'S COMPLEMENT FRACTIONS
For simplicity, the word size is assumed to be 4 bits. It will be generalized to n bits later. The word 0 001 is interpreted as 0.001 if it is a 2's complement fraction. Just as 0.345 decimal has the value 3 × 10−1 + 4 × 10−2 + 5 × 10−3, the bit sequence 0.001 will have the value 0 × 2−1 + 0 × 2−2 + 1 × 2−3 = 0.125, and is treated as +0.125 as the MS bit is 0.
As another example, what is the value of 1 001, if the interpretation is that it is a 2's complement fraction? It is 1.001 assuming the binary point after the MS bit. As the MS bit is 1, it is a negative number. Then the remaining bits do not specify the magnitude directly. The 2's complement of 1 000 is 0110 + 1 = 0 111. This is a positive fraction with the value 1 × 2−1 + 1 × 2−2 + 1 × 2−3 = 0.5 + 0.25 + 0.125 = 0.875 decimal. Thus, -0.875 is the value of 1 001.
A tabular column of signed decimal fractions and their equivalent in 2's complement notation is shown below, assuming a word size of 4 bits.
| Fraction | 2's complement notation |
| +0.5 | 0 100 |
| -0.5 | 1 100 |
| +0.25 | 0 001 Smallest magnitude non-zero value is 2−3 |
| -0.25 | 1 111 Smallest magnitude non-zero value is 2−3 |
| +0.875 | 0 111 Largest positive magnitude value is (1-2−3) |
| -0.875 | 1 001 |
| -1.0 | 1 000 Largest negative magnitude value is 1.0 |
| 0 | 0 000 |
From the above, it is obvious that if the word size is n bits, the smallest magnitude non-zero fraction that can be represented is 2(n-1). A table of word size and the smallest magnitude fraction that can be represented is shown in the following.
| Word size | Smallest magnitude 2's complement fraction |
| 4 | ±0.125 |
| 8 | ±0.0078125 |
| 16 | ±0.0000305 |
| 32 | ±0.5 × 10−9 |
In other words, when the word size is only 4 bits, it is not possible to represent a number like -0.0123 quite accurately. The minimum word size has to be 8 bits to represent the number -0.0123 somewhat accurately. The accuracy is very much improved if the word size is further increased.
 3.4 SIGNED FLOATING POINT NUMBERS
3.4 SIGNED FLOATING POINT NUMBERS
In our daily life, we work many times with real numbers, which will have an integer part and a fractional part. An example is 23.456. But this notation is not convenient for representing very large magnitude numbers, like -123456789.4567. This same number can be more conveniently represented in scientific notation as -1.2345678 × 10+08. But this actually stands for -123456780. So there is an error of 9.4567, which forms a very small percentage error.
However, the advantage of this scientific notation is that a very much larger number than -1.2345678 × 10+8 can be represented using same number of digits. For example, +9.9999999 × 10+99 is the largest magnitude positive number using same number of digits.
Similarly, the way we represent real numbers in our daily life is not convenient for representing very small numbers, like +0.00000045678912. This same number can be more conveniently represented in scientific notation as +4.56789 × 10−07. But this actually stands for +0.000000456789. So there is an error of 0.00000000000012, which forms a very small percentage error.
However, the advantage of this scientific notation is that a very much smaller magnitude number than +4.56789 × 10−07 can be represented using same number of digits. For example, -1.00000 × 10−99 is the smallest magnitude negative number using the same number of digits.
Using fixed-point notation, when the word size is as large as 32 bits, the largest magnitude signed integer that can be represented is approximately ±2 × 10+09 only. And the smallest non-zero magnitude signed fraction that can be represented is approximately ±0.5 × 10−09 only when the word size is 32bits.
So to represent very large, or very small signed numbers, with a word size of say, 32 bits, a computer uses floating point notation. This may result in small errors, but the error will be negligible, if large number of digits is reserved for the fractional part. But the important thing is that much larger range of numbers can be represented than is possible with fixed-point notation.
A floating-point number like +1.23 × 104 can be written in several equivalent ways as +12.3 × 103 or +0.123 × 105.
Similarly, there are several ways of representing floating point numbers in a computer also. As an example, in the 32-bit floating point notation used in Intel 8087 numeric co-processor, the largest magnitude number is approximately ±5.12 × 10+38 and the smallest magnitude number is approximately ±8 × 10−39. The interested reader can refer to the book ‘Advanced Microprocessors and IBM-PC Assembly Language Programming’ by Udaya kumar and Umashankar (Tata McGraw Hill Publication) for more details.
- Give examples for unsigned integers, signed integers, and floating point numbers.
- Explain how unsigned numbers are represented in a digital computer. If such numbers are represented using 16 bits, what will be the range?
- Explain how signed numbers are represented in a digital computer using SM notation. If such numbers are represented using 32 bits, what will be the range?
- Explain how signed numbers are represented in a digital computer using 1?'s complement notation. If such numbers are represented using 8 bits, what will be the range?
- Explain how signed numbers are represented in a digital computer using 2's complement notation. If such numbers are represented using 64 bits, what will be the range?
- Fill up the following table with the values of the bit sequences in unsigned integer, SM integer, etc.

- What are the advantages of 2's complement notation over SM and 1's complement notations in representing signed numbers?
- How can fractions be represented in a computer using fixed-point notation? Explain the 2's complement method of representing fixed-point fractions.