Steps in Conducting Principal Component Analysis
Principal component analysis is normally conducted in a sequence of steps, with somewhat subjective decisions being made at various points. Because this is an introductory treatment of the topic, it will not provide a comprehensive discussion of all options available at each step; instead, specific recommendations will be made, consistent with practices commonly followed in applied research. For a more detailed treatment of principal component analysis and factor analysis, see Kim and Mueller (1978a; 1978b), Rummel (1970), or Stevens (2002).
Step 1: Initial Extraction of the Components
In principal component analysis, the number of components extracted is equal to the number of variables analyzed. Because six variables are analyzed in the present study, six components are extracted. The first component can be expected to account for a fairly large amount of total variance. Each succeeding component accounts for progressively smaller amounts of variance. Although a large number of components can be extracted in this way, only the first few components are sufficiently important to be retained for interpretation.
Page 2 of Output 15.1 provides the eigenvalue table from the analysis. (This table appears just below the heading “Eigenvalues of the Correlation Matrix: Total = 6 Average = 1.”) An eigenvalue represents the amount of variance that is captured by a given component. In the column headed “Eigenvalue,” the eigenvalue for each component is presented. Each row in the matrix presents information about each of the six components. Row 1 provides information about the first component extracted, row 2 provides information about the second component extracted, and so forth.
Where the column headed EIGENVALUE intersects with rows “1” and “2,” it can be seen that the eigenvalue for component 1 is approximately 2.27 while the eigenvalue for component 2 is 1.97. This pattern is consistent with our earlier statement that the first components tend to account for relatively large amounts of variance whereas the later components account for relatively smaller amounts.
Step 2: Determining How Many “Meaningful” Components to Retain
Earlier, it was stated that the number of components extracted is equal to the number of variables analyzed. This requires that you decide just how many of these components are truly meaningful and worthy of being retained for rotation and interpretation. In general, you expect that only the first few components will account for meaningful amounts of variance and that the later components will tend to account for only trivial variance. The next step of the analysis, therefore, is to determine how many meaningful components should be retained for interpretation. This section describes four criteria that can be used in making this decision: the eigenvalue-one criterion; the scree test; the proportion of variance accounted for; and the interpretability criterion.
A. The Eigenvalue-One Criterion. In principal component analysis, one of the most commonly used criteria for solving the number-of-components problem is the eigenvalue-one criterion, also known as the Kaiser-Guttman criterion (Kaiser, 1960). With this approach, you retain and interpret any component with an eigenvalue greater than 1.00.
The rationale for this criterion is straightforward. Each observed variable contributes one unit of variance to the total variance in the dataset. Any component that displays an eigenvalue greater than 1.00 is accounting for a greater amount of variance than had been contributed by one variable. Such a component therefore accounts for a meaningful amount of variance and is worthy of retention.
On the other hand, a component with an eigenvalue less than 1.00 accounts for less variance than contributed by one variable. The purpose of principal component analysis is to reduce a number of observed variables into a relatively smaller number of components. This cannot be effectively achieved if you retain components that account for less variance than had been contributed by individual variables. For this reason, components with eigenvalues less than 1.00 are viewed as trivial and are not retained.
The eigenvalue-one criterion has a number of positive features that contribute to its popularity. Perhaps the most important reason for its widespread use is its simplicity. You do not make subjective decisions but merely retain components with eigenvalues greater than one.
On the positive side, it has been shown that this criterion very often results in retaining the correct number of components, particularly when a small-to-moderate number of variables are analyzed, and the variable communalities are high. Stevens (2002) reviews studies that have investigated the accuracy of the eigenvalue-one criterion and recommends its use when fewer than 30 variables are being analyzed and communalities are greater than .70, or when the analysis is based on more than 250 observations and the mean communality is greater than .59.
There are several problems associated with the eigenvalue-one criterion, however. As suggested in the preceding paragraph, it can lead to retaining the wrong number of components under circumstances that are often encountered in research (e.g., when many variables are analyzed, when communalities are small). Also, the automatic application of this criterion can lead to retaining a certain number of components when the actual difference in the eigenvalues of successive components is trivial. For example, if component 2 displays an eigenvalue of 1.01 and component 3 displays an eigenvalue of 0.99, then component 2 is retained but component 3 is not. This might mislead you to believe that the third component was meaningless when, in fact, it accounted for almost exactly the same amount of variance as the second component. In short, the eigenvalue-one criterion can be helpful when used judiciously; yet, the automatic application of this approach can lead to serious errors of interpretation.
With SAS, the eigenvalue-one criterion can be implemented by including the MINEIGEN=1 option in the PROC FACTOR statement and not including the NFACT option. The use of MINEIGEN=1 causes PROC FACTOR to retain any component with an eigenvalue greater than 1.00.
The eigenvalue table from the current analysis appears on page 2 of Output 15.1. The eigenvalues for components 1, 2, and 3 were 2.27, 1.97, and 0.80, respectively. Only components 1 and 2 demonstrated eigenvalues greater than 1.00 so the eigenvalue-one criterion would lead you to retain and interpret only these two components.
Fortunately, the application of the criterion is fairly unambiguous in this case. The last component retained (2) displays an eigenvalue of 1.97, which is substantially greater than 1.00, and the next component (3) displays an eigenvalue of 0.80, which is clearly lower than 1.00. In this analysis, you are not faced with the difficult decision of whether to retain a component that demonstrates an eigenvalue approaching 1.00 (e.g., an eigenvalue of .99). In situations such as this, the eigenvalue-one criterion can be used with greater confidence.
B. The Scree Test. With the scree test (Cattell, 1966), you plot the eigenvalues associated with each component and look for a definitive “break” between the components with relatively large eigenvalues and those with small eigenvalues. The components that appear before the break are assumed to be meaningful and are retained for rotation whereas those appearing after the break are assumed to be unimportant and are not retained. Sometimes, a scree plot displays several large breaks. When this is the case, you should look for the last big break before the eigenvalues begin to level off. Only the components that appear before this last large break should be retained.
Specifying the SCREE option in the PROC FACTOR statement causes SAS to print an eigenvalue plot as part of the output. This appears as page 3 of Output 15.1.
You can see that the component numbers are listed on the horizontal axis, while eigenvalues are listed on the vertical axis. With this plot, notice that there is a relatively small break between components 1 and 2, and a relatively large break following component 2. The breaks between components 3, 4, 5, and 6 are all relatively small. It is often helpful to draw long lines with extended tails connecting successive pairs of eigenvalues so that these breaks are more apparent (e.g., measure degrees separating lines with a protractor).
Because the large break in this plot appears between components 2 and 3, the scree test would lead you to retain only components 1 and 2. The components appearing after the break (3 to 6) would be regarded as trivial.
The scree test can be expected to provide reasonably accurate results, provided that the sample is large (more than 200) and most of the variable communalities are large (Stevens, 2002). However, this criterion has its weaknesses as well, most notably the ambiguity that is often displayed by scree plots under typical research conditions. Very often, it is difficult to determine exactly where in the scree plot a break exists, or even if a break exists at all. In contrast to the eigenvalue-one criterion, the scree test is generally more subjective.
The break in the scree plot on page 3 of Output 15.1 was unusually obvious. In contrast, consider the plot in Figure 15.2.
Figure 15.2. A Scree Plot with No Obvious Break
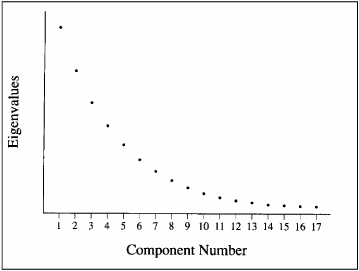
Figure 15.2 presents a fictitious scree plot from a principal component analysis of 17 variables. Notice that there is no obvious break in the plot that separates the meaningful components from the trivial components. Most researchers would agree that components 1 and 2 are probably meaningful whereas components 13 to 17 are probably trivial; however, it is difficult to decide exactly where you should draw the line. This example underscores the qualitative nature of judgments based solely on the scree test.
Scree plots such as the one presented in Figure 15.2 are common in social science research. When encountered, the use of the scree test must be supplemented with additional criteria such as the variance accounted for criterion and the interpretability criterion, to be described later.
Why do they call it a “scree” test?The word “scree” refers to the loose rubble that lies at the base of a cliff or glacier. When performing a scree test, you normally hope that the scree plot will take the form of a cliff. At the top will be the eigenvalues for the few meaningful components, followed by a definitive break (the edge of the cliff). At the bottom of the cliff will lie the scree (i.e., eigenvalues for the trivial components). |
C. Proportion of variance accounted for. A third criterion to address the number of factors problem involves retaining a component if it exceeds a specified proportion (or percentage) of variance in the dataset. For example, you might decide to retain any component that accounts for at least 5% or 10% of the total variance. This proportion can be calculated with a simple formula:
![]()
In principal component analysis, the “total eigenvalues of the correlation matrix” is equal to the total number of variables being analyzed (because each variable contributes one unit of variance to the analysis).
Fortunately, it is not necessary to manually compute these percentages since they are provided in the results of PROC FACTOR. The proportion of variance captured by each component is printed in the eigenvalue table (page 2) under the “Proportion” heading.
The eigenvalue table for the current analysis is on page 2 of Output 15.1. From the “Proportion” column, you can see that the first component alone accounts for 38% of the total variance, the second component alone accounts for 33%, the third component accounts for 13%, and the fourth component accounts for 7%. Assume that you have decided to retain any component that accounts for at least 10% of the total variance in the dataset. For the present results, using this criterion would cause you to retain components 1, 2, and 3. (Notice that use of this criterion would result in retaining more components than would be retained with the two preceding criteria.)
An alternative criterion is to retain enough components so that the cumulative percent of variance accounted for is equal to some minimal value. For example, remember that components 1, 2, 3, and 4 accounted for approximately 38%, 33%, 13% and 7% of the total variance, respectively. Adding these percentages together results in a sum of 91%. This means that the cumulative percent of variance accounted for by components 1, 2, 3 and 4 is 91%. When researchers use the “cumulative percent of variance accounted for” as the criterion for solving the number-of-components problem, they usually retain enough components so that the cumulative percent of variance accounted for at least 70% (and sometimes 80%).
With respect to the results of PROC FACTOR, the “cumulative percent of variance accounted for” is presented in the eigenvalue table (from page 2), below the “Cumulative” heading. For the present analysis, this information appears in the eigenvalue table on page 2 of Output 15.1. Notice the values that appear below the heading “Cumulative.” Each value indicates the percent of variance accounted for by the present component as well as all preceding components. For example, the value for component 2 is approximately .71 (intersection of the column labeled “Cumulative” and the second row). This value of .71 indicates that approximately 71% of the total variance is accounted for by components 1 and 2. The corresponding entry for component 3 is approximately .84, indicating that 84% of the variance is accounted for by components 1, 2, and 3. If you were to use 70% as the “critical value” for determining the number of components to retain, you would retain components 1 and 2 in the present analysis.
The proportion of variance criterion has a number of positive features. For example, in most cases, you would not want to retain a group of components that, combined, account for only a fraction of variance in the dataset (say, 30%). Nonetheless, the critical values discussed earlier (10% for individual components and 70% to 80% for the combined components) are quite arbitrary. Because of these and related problems, this approach has sometimes been criticized for its subjectivity (Kim & Mueller, 1978b).
D. The interpretability criteria. Perhaps the most important criterion for solving the “number-of-components” problem is the interpretability criterion: interpreting the substantive meaning of the retained components and verifying that this interpretation makes sense in terms of what is known about the constructs under investigation. The following list provides four rules to follow when doing this. A later section (“Step 4: Interpreting the Rotated Solution”) shows how to interpret the results of a principal component analysis. The following rules will be more meaningful after you complete that section.
Are there at least three variables (items) with significant loadings on each retained component? A solution is less satisfactory if a given component is measured by fewer than three variables.
Do the variables that load on a given component share the same conceptual meaning? For example, if three questions on a survey all load on component 1, do all three of these questions appear to be measuring the same construct?
Do the variables that load on different components seem to be measuring different constructs? For example, if three questions load on component 1 and three other questions load on component 2, do the first three questions seem to be measuring a construct that is conceptually distinct from the construct measured by the last three questions?
Does the rotated factor pattern demonstrate “simple structure”? Simple structure means that the pattern possesses two characteristics: (a) most of the variables have relatively high factor loadings on only one component and near-zero loadings on the other components; and (b) most components have relatively high factor loadings for some variables and near-zero loadings for the remaining variables. This concept of simple structure is explained in more detail in a later section, “Step 4: Interpreting the Rotated Solution.”
Recommendations
Given the preceding options, what procedure should you follow in solving the number-of-components problem? We recommend combining all four in a structured sequence. First, use the MINEIGEN=1 options to implement the eigenvalue-one criterion. Review this solution for interpretability but use caution if the break between the components with eigenvalues above 1.00 and those below 1.00 is not clear-cut (i.e., if component 1 has an eigenvalue of 1.01, and component 2 has an eigenvalue of 0.99).
Next, perform a scree test and look for obvious breaks in eigenvalues. Because there often is more than one break in the scree plot, it might be necessary to examine two or more possible solutions.
Next, review the amount of common variance accounted for by each individual component. You probably should not rigidly use some specific but arbitrary cutoff point such as 5% or 10%. Still, if you are retaining components that account for as little as 2% or 4% of the variance, it might be wise to take a second look at the solution and verify that these latter components are truly of substantive importance. In the same way, it is best if the combined components account for at least 70% of cumulative variance. If less than 70% is captured, it might be prudent to consider alternate solutions that include a larger number of components.
Finally, apply the interpretability criteria to each solution. If more than one solution can be justified on the basis of the preceding criteria, which of these solutions is the most interpretable? By seeking a solution that is both interpretable and also satisfies one (or more) of the other three criteria, you maximize chances of retaining the optimal number of components.
Step 3: Rotation to a Final Solution
Factor Patterns and Factor Loadings
After extracting the initial components, PROC FACTOR creates an unrotated factor pattern matrix. The rows of this matrix represent the variables being analyzed, and the columns represent the retained components. (These components are referred to as FACTOR1, FACTOR2, and so forth in the output.)
The entries in the matrix are factor loadings. A factor loading is a general term for a coefficient that appears in a factor pattern matrix or a factor structure matrix. In an analysis that results in oblique (correlated) components, the definition for a factor loading is different depending on whether it is in a factor pattern matrix or in a factor structure matrix. However, the situation is simpler in an analysis that results in orthogonal components (as in the present chapter). In an orthogonal analysis, factor loadings are equivalent to bivariate correlations between the observed variables and the components.
For example, the factor pattern matrix from the current analysis is on page 4 of Output 15.1. Where the rows for observed variables intersect with the column for FACTOR1, you can see that the correlation between V1 and the first component is .58; the correlation between V2 and the first component is .48, and so forth.
Rotations
Ideally, you would like to review the correlations between the variables and the components, and use this information to interpret the components. That is, to determine what construct seems to be measured by component 1, what construct seems to be measured by component 2, and so forth. Unfortunately, when more than one component is retained in an analysis, the interpretation of an unrotated factor pattern is usually quite difficult. To facilitate interpretation, you normally perform an operation called a rotation. A rotation is a linear transformation that is performed on the factor solution for the purpose of making the solution easier to interpret.
PROC FACTOR allows you to request several different types of rotations. The preceding program that analyzed data from the POI study included the statement
ROTATE=VARIMAX
which requests a varimax rotation. A varimax rotation is an orthogonal rotation, meaning that it results in uncorrelated components. Compared to other types of rotations, a varimax rotation tends to maximize the variance of a column of the factor pattern matrix (as opposed to a row of the matrix). This rotation is probably the most commonly used orthogonal rotation in the social sciences. The results of the varimax rotation for the current analysis are on page 5 of Output 15.1.
Step 4: Interpreting the Rotated Solution
Interpreting a rotated solution means determining just what is measured by each of the retained components. Briefly, this involves identifying the variables that exhibit high loadings for a given component, and determining what these variables share in common. Usually, a brief name is assigned to each retained component to describe its content.
The first decision to be made at this stage is to decide how large a factor loading must be in order to be considered “large.” Stevens (2002) discusses some of the issues relevant to this decision and provides guidelines for testing the statistical significance of factor loadings. Given that this is an introductory treatment of principal component analysis, consider a loading to be “large” if its absolute value exceeds .40.
The rotated factor pattern for the POI study appears on page 5 of Output 15.1. The following text provides a structured approach for interpreting this factor pattern.
A. Read across the row for the first variable. All “meaningful loadings” (i.e., loadings greater than .40) are flagged with an asterisk (“*”). This was accomplished by including the FLAG=.40 option in the preceding program. If a given variable has a meaningful loading on more than one component, scratch that variable out and ignore it in your interpretation. In many situations, researchers want to drop variables that load on more than one component because the variables are not pure measures of any one construct. (These are sometimes referred to as complex items.) In the present case, this means looking at the row headed “V1,” and reading to the right to see if it loads on more than one component. In this case it does not, so you can retain this variable.
B. Repeat this process for the remaining variables, scratching out any variable that loads on more than one component. In this analysis, none of the variables have high loadings on more than one component, so none has to be deleted. In other words, there are no complex items.
C. Review all of the surviving variables with high loadings on component 1 to determine the nature of this component. From the rotated factor pattern, you can see that only items 4, 5, and 6 load on component 1 (note the asterisks). Now, turn to the questionnaire itself and review the content in order to decide what a given component should be named. What do questions 4, 5, and 6 have in common? What common construct do they appear to be measuring? For illustration, the questions being analyzed in the present case are reproduced here. Remember that question 4 is represented as V4 in the SAS program, question 5 is V5, and so forth. Read questions 4, 5, and 6 to see what they have in common.
1 2 3 5 6 7 1. Went out of my way to do |
Questions 4, 5, and 6 all seem to deal with “giving money to those in need.” It is therefore reasonable to label component 1 the “financial giving” component.
D. Repeat this process to name the remaining retained components. In the present case, there is only one remaining component to name: component 2. This component has high loadings for questions 1, 2, and 3. In reviewing these items, it becomes clear that each seems to deal with helping friends, relatives, or other acquaintances. It is therefore appropriate to name this the “helping others” component.
E. Determine whether this final solution satisfies the interpretability criteria. An earlier section indicated that the overall results of a principal component analysis are satisfactory only if they meet a number of interpretability criteria. In the following list, the adequacy of the rotated factor pattern presented on page 5 of Output 15.1 is assessed in terms of these criteria.
Are there at least three variables (items) with significant loadings on each retained component? In the present example, three variables load on component 1 and three load on component 2, so this criterion is met.
Do the variables that load on a given component share similar conceptual meaning? All three variables loading on component 1 measure giving to those in need, while all three loading on component 2 measure prosocial acts performed for others. Therefore, this criterion is met.
Do the variables that load on different components seem to be measuring different constructs? The items loading on component 1 measure respondents’ financial contributions, while the items loading on component 2 measure helpfulness toward others. Because these seem to be conceptually distinct constructs, this criterion appears to be met as well.
Does the rotated factor pattern demonstrate “simple structure”? Earlier, it was said that a rotated factor pattern demonstrates simple structure when it has two characteristics. First, most of the variables should have high loadings on one component and near-zero loadings on the other components. It can be seen that the pattern obtained here meets that requirement: items 1 through 3 have high loadings on component 2 and near-zero loadings on component 1. Similarly, items 4 through 6 have high loadings on component 1 and near-zero loadings on component 2. The second characteristic of simple structure is that each component should have high loadings for some variables and near-zero loadings for the others. Again, the pattern obtained here meets this requirement: component 1 has high loadings for items 4 through 6 and near-zero loadings for the other items whereas component 2 has high loadings for items 1 through 3 and near-zero loadings on the remaining items. In short, the rotated component pattern obtained in this analysis appears to demonstrate simple structure.
Step 5: Creating Factor Scores or Factor-Based Scores
Once the analysis is complete, it is often desirable to assign scores to participants to indicate where they stand on the retained components. For example, the two components retained in the present study were interpreted as financial giving and helping others. You might want to now assign one score to each participant to indicate that participant’s standing on the financial giving component and a different score to indicate his/her standing on the helping others component. With this done, these component scores could be used either as predictor variables or as criterion variables in subsequent analyses.
Before discussing the options for assigning these scores, it is important to first draw a distinction between factor scores versus factor-based scores. In principal component analysis, a factor score (or component score) is a linear composite of the optimally weighted observed variables. If requested, PROC FACTOR computes each participant’s factor scores for the two components by:
determining the optimal regression weights;
multiplying participant responses to the questionnaire items by these weights;
summing the products.
The resulting sum is a given participant’s score on the component of interest. Remember that a separate equation with different weights is developed for each retained component.
A factor-based score, on the other hand, is merely a linear composite of the variables that demonstrate meaningful loadings for the component in question. In the preceding analysis, for example, items 4, 5, and 6 demonstrated meaningful loadings for the financial giving component. Therefore, you could calculate the factor-based score on this component for a given participant by simply adding together his or her responses to items 4, 5, and 6. Notice that, with a factor-based score, the observed variables are not multiplied by optimal weights before they are summed.
Computing Factor Scores
Factor scores are requested by including the NFACT and OUT options in the PROC FACTOR statement. Here is the general form for a SAS program that uses the NFACT and OUT option to compute factor scores:
PROC FACTOR DATA=dataset-name
SIMPLE
METHOD=PRIN
PRIORS=ONE
NFACT=number-of-components-to-retain
ROTATE=VARIMAX
ROUND
FLAG=desired-size-of-"significant"-factor-loadings
OUT=name-of-new-SAS-dataset ;
VAR variables-to-be-analyzed ;
RUN;Here are the actual program statements (minus the DATA step) that could be used to perform a principal component analysis and compute factor scores for the POI study.
1 PROC FACTOR DATA=D1 2 SIMPLE 3 METHOD=PRIN 4 PRIORS=ONE 5 NFACT=2 6 ROTATE=VARIMAX 7 ROUND 8 FLAG=.40 9 OUT=D2 ; 10 VAR V1 V2 V3 V4 V5 V6; 11 RUN;
Notice how this program differs from the original program presented earlier in the chapter (in “SAS Program and Output”). The MINEIGEN=1 option has been dropped and is replaced with the NFACT=2 option. The OUT=D2 option also is added.
Line 9 of the preceding programs asks that an output dataset be created and given the name D2. This name is arbitrary; any name consistent with SAS requirements is acceptable. The new dataset named D2 will contain all of the variables contained in the previous dataset (D1), as well as new variables named FACTOR1 and FACTOR2. FACTOR1 will contain factor scores for the first retained component and FACTOR2 will contain scores for the second. The number of new “FACTOR” variables created will be equal to the number of components retained by the NFACT statement.
The OUT option can be used to create component scores only if the analysis is performed on a raw dataset (as opposed to a correlation or covariance matrix). The use of the NFACT statement is also required.
Having created the new variables named FACTOR1 and FACTOR2, you might be interested in seeing how they relate to the study’s original observed variables. This can be done by appending PROC CORR statements to the SAS program, following the last of the PROC FACTOR statements. The full program (minus the DATA step) is:
1 PROC FACTOR DATA=D1 2 SIMPLE 3 METHOD=PRIN 4 PRIORS=ONE 5 NFACT=2 6 ROTATE=VARIMAX 7 ROUND 8 FLAG=.40 9 OUT=D2 ; 10 VAR V1 V2 V3 V4 V5 V6; 11 RUN; 12 13 PROC CORR DATA=D2; 14 VAR FACTOR1 FACTOR2; 15 WITH V1 V2 V3 V4 V5 V6 FACTOR1 FACTOR2; 16 RUN;
Notice that the PROC CORR statement on line 13 specifies DATA=D2. This dataset (D2) is the name of the output dataset created on line 9 in the PROC FACTOR statement. The PROC CORR statements request that the factor score variables (FACTOR 1 and FACTOR2) be correlated with participants’ responses to questionnaire items 1 through 6 (V1 to V6).
With printer options of LINESIZE=80 and PAGESIZE=60 (first line), the preceding program would again produce four pages of output. Pages 1 to 2 provide simple statistics, the eigenvalue table, and the unrotated factor pattern, identical to those produced with the first program. Page 3 provides the rotated factor pattern and final communalities (same as before), along with the standardized scoring coefficients used in creating factor scores. Finally, page 4 provides the correlations requested by the CORR procedure. Pages 3 and 4 of the output created by the preceding program are presented here as Output 15.2.
Output 15.2. Output Pages 3 and 4 from the Analysis of POI Data in Which Factor Scores Were Created

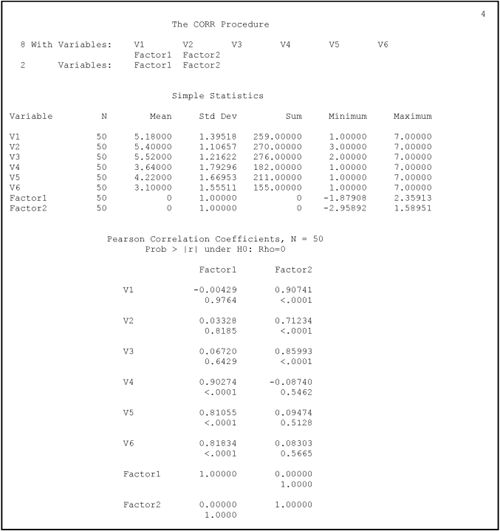
The simple statistics for the CORR procedure appear on page 4 in Output 15.2. Notice that the simple statistics for the observed variables (V1 to V6) are identical to those at the beginning of the FACTOR output discussed earlier (at the top of Output 15.1, page 1). In contrast, note the simple statistics for FACTOR1 and FACTOR2 (the factor score variables for components 1 and 2, respectively). Both have means of 0 and standard deviations of 1. Obviously, these variables were constructed to be standardized variables.
The correlations between FACTOR1 and FACTOR2 and the original observed variables appear on the bottom half of page 4. You can see that the correlations between FACTOR1 and V1 through V6 on page 4 of Output 15.2 are identical to the factor loadings of V1 through V6 on FACTOR1 on page 5 of Output 15.1, under “Rotated Factor Pattern.” This makes sense, as the elements of a factor pattern (in an orthogonal solution) are simply correlations between the observed variables and the components themselves. Similarly, you can see that the correlations between FACTOR2 and V1 through V6 from page 4 of Output 15.2 are also identical to the corresponding factor loadings from page 5 of Output 15.1.
Of special interest is the correlation between FACTOR1 and FACTOR2, as computed by PROC CORR. This appears on page 4 of Output 15.2, where the row for FACTOR2 intersects with the column for FACTOR1. Notice the observed correlation between these two components is zero. This is as expected; the rotation method used in this principal component analysis is the varimax method which produces orthogonal, or uncorrelated, components.
Computing Factor-Based Scores
A second (and less sophisticated) approach to scoring involves the creation of new variables that contain factor-based scores rather than true factor scores. A variable that contains factor-based scores is sometimes referred to as a factor-based scale.
Although factor-based scores can be created several ways, the following method has the advantage of being relatively straightforward and is commonly used:
To calculate factor-based scores for component 1, determine which questionnaire items had high loadings on that component.
For a given participant, add together that participant’s responses to these items. The result is that participant’s score on the factor-based scale for component 1.
Repeat these steps to calculate each participant’s score on the remaining retained components.
Although this might sound like a cumbersome task, it is actually made quite simple through the use of data manipulation statements contained in a SAS program. For example, assume that you have performed the principal component analysis on your survey responses and have obtained the findings reported in this chapter. Specifically, you found that survey items 4, 5, and 6 loaded on component 1 (the financial giving component), while items 1, 2, and 3 loaded on component 2 (helping others component).
You would now like to create two new SAS variables. The first variable, called FINANCE, will include each participant’s factor-based score for financial giving. The second variable, called HELPING, will include each participant’s factor-based score for helping others. Once these variables are created, they can be used as criterion or predictor variables in subsequent analyses. To keep things simple, assume that you are simply interested in determining whether or not there is a significant correlation between FINANCE and HELPING.
At this time, it might be useful to review Chapter 4, “Working with Variables and Observations in SAS Datasets,” particularly the section on creating new variables from existing variables. Such a review should make it easier to understand the data manipulation statements used here.
Assume that earlier statements in the SAS program have already input responses to the six questionnaire items. These variables are included in a dataset called D1. The following are the subsequent lines that would go on to create a new dataset called D2. The new dataset will include all of the variables in D1, as well as the newly created factor-based scales called FINANCE and HELPING.
14 15 DATA D2; 16 SET D1; 17 18 FINANCE = (V4 + V5 + V6); 19 HELPING = (V1 + V2 + V3); 20 21 PROC CORR DATA=D2; 22 VAR FINANCE HELPING; 23 RUN;
Lines 15 and 16 request that a new dataset called D2 be created, and that it be set up as a duplicate of existing dataset D1. In line 18, the new variable called FINANCE is created. For each participant, his or her responses to items 4, 5, and 6 are added together. The result is the participant’s score on the factor-based scale for the first component. These scores are stored as a variable called FINANCE. The component-based scale for the helping others component is created on line 19, and these scores are stored as the variable called HELPING. Lines 21 to 23 request that the correlations between FINANCE and HELPING be determined. FINANCE and HELPING can now be used as predictor or criterion variables in subsequent analyses. To save space, the results of this program are not reproduced here.
However, note that this output would probably display a nonzero correlation between FINANCE and HELPING. This might come as a surprise, because earlier it was shown that the factor scores contained in FACTOR1 and FACTOR2 (counterparts to FINANCE and HELPING) were completely uncorrelated. The reason for this apparent contradiction is simple: FACTOR1 and FACTOR2 are true principal components; true principal components (created in an orthogonal solution) are always created with optimally weighted equations so that they will be mutually uncorrelated.
In contrast, FINANCE and HELPING are not true principal components that consist of true factor scores; they are merely variables based on the results of a principal component analysis. Optimal weights (that would ensure orthogonality) were not used in the creation of FINANCE and HELPING. This is why factor-based scales will often demonstrate nonzero correlations with one another while true principal components (from an orthogonal solution) will not.
Recoding Reversed Items prior to Analysis
It generally is best to recode any reversed items before conducting any of the analyses described here. In particular, it is essential that reversed items be recoded prior to the program statements that produce factor-based scales. For example, the three questionnaire items that assess financial giving appear again here:
1 2 3 4 5 6 7 4. Gave money to a religious |
None of these items are reversed. With each item, a response of “7” indicates a high level of financial giving. In the following, however, item 4 is a reversed item: with item 4, a response of “7” indicates a low level of giving:
1 2 3 4 5 6 7 4. Refused to give money to |
If you were to perform a principal component analysis on responses to these items, the factor loading for item 4 would most likely have a sign that is opposite of the sign of the loadings for items 5 and 6 (e.g., if items 5 and 6 had positive loadings, item 4 would have a negative loading). This would complicate the creation of a component-based scale: with items 5 and 6, higher scores indicate greater giving whereas with item 4, lower scores indicate greater giving. You would not want to sum these three items as they are presently coded. First, it is necessary to reverse item 4. Notice how this is done in the following program (assume that the data have already been entered in a SAS dataset named D1):
15 DATA D2; 16 SET D1; 17 18 V4 = 8 - V4; 19 20 FINANCE = (V4 + V5 + V6); 21 HELPING = (V1 + V2 + V3); 22 23 PROC CORR DATA=D2; 24 VAR FINANCE HELPING; 25 RUN;
Line 18 creates a new, recoded version of variable V4. Values on this new version of V4 are equal to the quantity 8 minus the value of the old version of V4. For participants whose score on the old version of V4 is 1, their value on the new version of V4 is 7 (because 8 – 1 = 7). For those whose score is 7, their value on the new version of V4 is 1 (8 – 7 = 1). See Chapter 4 for further description of this procedure.
The general form of the formula used when recoding reversed items is
Variable-name = constant - variable-name ;
In this formula, the “constant” is the following quantity:
the number of points on the response scale used with the questionnaire item plus 1.
Therefore, if you are using the 4-point response format, the constant is 5. If using a 9-point scale, the constant is 10.
If you have prior knowledge about which items are going to appear as reversed (with reversed component loadings) in your results, it is best to place these recoding statements early in your SAS program before the PROC FACTOR statements. This makes interpretation of the components more straightforward because it eliminates significant loadings with opposite signs from appearing on the same component. In any case, it is essential that the statements recoding reversed items appear before the statements that create any factor-based scales.
Step 6: Summarizing the Results in a Table
For reports that summarize the results of your analysis, it is generally desirable to prepare a table that presents the rotated factor pattern. When analyzed variables contain responses to questionnaire items, it can be helpful to actually reproduce the questionnaire items within this table. This is done in Table 15.2:
| Component | |||
|---|---|---|---|
| 1 | 2 | h2 | Items |
| .00 | .91 | .82 | 1. Went out of my way to do a favor for a coworker. |
| .03 | .71 | .51 | 2. Went out of my way to do a favor for a relative. |
| .07 | .86 | .74 | 3. Went out of my way to do a favor for a friend. |
| .90 | -.09 | .82 | 4. Gave money to a religious charity. |
| .81 | .09 | .67 | 5. Gave money to a charity not associated with a religion. |
| .82 | .08 | .68 | 6. Gave money to a panhandler. |
| Note. | N = 50. | Communality estimates appear in column headed h2. | |
The final communality estimates from the analysis are presented under the heading “h2” in the table. These estimates appear in the SAS output following the “Variance Explained By Each Factor” (page 3 of Output 15.2).
Very often, the items that constitute the questionnaire are so lengthy, or the number of retained components is so large that it is not possible to present the factor pattern, the communalities, and the items themselves in the same table. In such situations, it might be preferable to present the factor pattern and communalities in one table and the items in a second (or in the text of the paper). Shared item numbers can then be used to associate each item with its corresponding factor loadings and communality.
Step 7: Preparing a Formal Description of the Results for a Paper
The preceding analysis could be summarized in the following way:
Principal component analysis was applied to responses to the 6-item questionnaire using 1s as prior communality estimates. The principal axis method was used to extract the components, and this was followed by a varimax (orthogonal) rotation.
Only the first two components exhibited eigenvalues greater than 1; results of a scree test also suggested that only the first two were meaningful. Therefore, only the first two components were retained for rotation. Combined, components 1 and 2 accounted for 71% of the total variance.
Questionnaire items and corresponding factor loadings are presented in Table 15.2. In interpreting the rotated factor pattern, an item was said to load on a given component if the factor loading was .40 or greater for that component and less than .40 for the other. Using these criteria, three items were found to load on the first component, which was subsequently labeled financial giving. Three items also loaded on the second component labeled helping others.
