The Results of a Multiple Regression Analysis

The Multiple Correlation Coefficient

The multiple correlation coefficient, symbolized as R, represents the strength of the relationship between a criterion variable and an optimally weighted linear combination of predictor variables. Its values can range from 0 through 1.00; it is interpreted in the same way a Pearson product-moment correlation coefficient (r) is interpreted (except that R can only assume positive values). Values approaching zero indicate little relationship between the criterion and the predictors whereas values near 1.00 indicate strong relationships. An R value of 1.00 indicates perfect or complete prediction of criteria values.

Conceptually, R should be viewed as the product-moment correlation between Y and Y′. This can be symbolized in the following way:

R = r_YY′

In other words, if you were to obtain data from a sample of participants that included their scores on Y as well as a number of X variables, computed Y′ scores for each participant, and then correlated predicted criterion scores (Y′) with actual scores (Y), the resulting bivariate correlation coefficient would be equivalent to R.

With bivariate regression, it is possible to estimate the amount of variance in Y that is accounted for by X by simply squaring the correlation between the two variables. The resulting product is sometimes referred to as the coefficient of determination. For example, if r = .50 for a given pair of variables, then their coefficient of determination can be computed as:

Coefficient of determination	= r2
	= (.50)2
	= .25

In this situation, therefore, it can be said the X variable accounts for 25% of the observed variance in the Y variable.

An analogous coefficient of determination can also be computed in multiple regression by simply squaring the observed multiple correlation coefficient, R. The resultant R² value (often referred to simply as R-squared) represents the percentage of variance in Y that is accounted for by the linear combination of predictor variables. The concept of “variance accounted for” is an extremely important one in multiple regression analysis and is therefore given detailed treatment in the following section.

Variance Accounted for by Predictor Variables: The Simplest Models

In multiple regression analyses, researchers often speak of “variance accounted for.” By this, they mean the percent of observed variance in the criterion variable accounted for by the linear combination of predictor variables.

A Single Predictor Variable

This concept is easier to understand by beginning with a simple bivariate example. Assume that you compute the correlation between prosocial behavior and moral development and find that r = .50 for these two variables. As was previously discussed, you can determine the percentage of variance in prosocial behavior that is accounted for by moral development by squaring this correlation coefficient:

r2	= (.50)2
	= .25

Thus, 25% of observed variance in prosocial behavior is accounted for by moral development. This can be illustrated graphically by using a Venn diagram in which the total variance in a variable is represented with a circle. The Venn diagram representing the correlation between prosocial behavior and moral development is in Figure 14.3:

Notice that the circle representing moral development overlaps the circle representing prosocial behavior. This indicates that the two variables are correlated. More specifically, the figure shows that there is an overlap of 25% of the area of the prosocial behavior circle by the moral development circle, meaning that moral development accounts for 25% of observed variance in prosocial behavior.

Multiple Predictor Variables with Intercorrelations of Zero

It is now possible to expand the discussion to the situation in which there are multiple X variables. Assume that you obtained data on prosocial behavior, age, income, and moral development from a sample of 100 participants and observe correlations among the four variables as summarized in Table 14.5:

Table 14.5. Correlation Matrix: Zero Correlations among X Variables

	Variable	Y	X1	X2	X3
Y	Prosocial behavior	1.00
X1	Age	.30	1.00
X2	Income	.40	.00	1.00
X3	Moral development	.50	.00	.00	1.00

When all possible correlations are computed for a set of variables, these correlations are usually presented in the form of a correlation matrix such as the one presented in Table 14.5. To find the correlation between two variables, you simply find the row for one variable, and the column for the second variable. The correlation between variables appears where the row intersects the column. For example, where the row for X₁ (age) intersects the column for Y (prosocial behavior), you see a correlation coefficient of r = .30.

You can use the preceding correlations to determine how much variance in Y is accounted for by the three X variables. For example, the correlation between age and prosocial behavior is r = .30; squaring this results in .09 (because .30 × .30 = .09). This means that age accounts for 9% of observed variance in prosocial behavior. Following the same procedure, you learn that income accounts for 16% of the variance in Y (because .40 × .40 = .16), while moral development continues to account for 25% of the variance in Y.

Notice another (somewhat unusual) fact concerning the correlations in this table: each of the X variables has a correlation of zero with all of the other X variables. For example, where the row for X₂ (income) intersects with the column for X₁ (age), you can see a correlation coefficient of .00. In the same way, Table 14.5 also shows correlations of .00 between X₂ and X₃, and between X₁ and X₃.

The correlations among the variables of Table 14.5 can be illustrated with the Venn diagram of Figure 14.4:

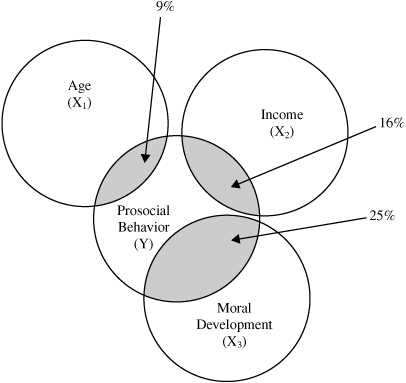
Notice two important points concerning the Venn diagram in Figure 14.4: each X variable accounts for some variance in Y but no X variable accounts for any variance in any other X variable. Because the preceding table showed that the X variables were uncorrelated, it is necessary to draw the Venn diagram so that there is no overlap between any of the X variables.

How much variance in Y is accounted for by the three predictors of Figure 14.4? This is easily determined by simply adding together the percent of variance accounted for by each of the three predictors individually:

Total variance accounted for	= .09 + .16 + .25
	= .50

The linear combination of X₁, X₂, and X₃ accounts for 50% of observed variance in prosocial behavior. In most areas of research in the social sciences, this would be considered a fairly large percentage of variance.

In the preceding example, the total variance in Y accounted for by the X variables was determined by simply summing the squared bivariate correlations between Y and the individual X variables. It is important to remember that you can use this procedure to determine the total variance accounted for in Y only when the X variables are completely uncorrelated with one another (which is rare). When there is any degree of correlation among the X variables, this approach gives misleading results. The reasons for this are discussed in the next section.

Variance Accounted for by Intercorrelated Predictor Variables

The preceding section shows that it is simple to determine the percent of variance in a criterion that is accounted for by a set of predictor variables when the predictor variables display zero correlation with one another. In that situation, the total variance accounted for will be equal to the sum of the squared bivariate correlations (i.e., the sum of r_Y1², r_Y2²... r_Yn²). The situation becomes much more complex, however, when the predictor variables are correlated with one another. In this situation, it is not possible to make simple statements about how much variance will be accounted for by a set of predictors.

In part, this is because multiple regression equations with correlated predictors behave one way when the predictors include a suppressor variable and behave a very different way when the predictors do not contain a suppressor variable. A later section will explain just what a suppressor variable is, and will describe the complexities that are introduced by this somewhat rare phenomenon. First, consider the (relatively) simpler situation that exists when the predictors included in a multiple regression equation are intercorrelated but do not contain a suppressor variable.

When Intercorrelated Predictors Do Not Include a Suppressor Variable

The preceding example was fairly unrealistic in that each X variable was said to have a correlation of zero with all of the other X variables. In nonexperimental research in the social sciences, you will almost never observe a set of predictor variables that are mutually uncorrelated in this way. Remember that nonexperimental research involves measuring naturally occurring (nonmanipulated) variables, and naturally occurring variables will almost always display some degree of intercorrelation.

For example, consider the nature of the variables studied here. Given that people tend to earn higher salaries as they grow older, it is likely that participant age would be positively correlated with income. Similarly, people with higher incomes might well demonstrate higher levels of moral development since they do not experience the deprivation and related stresses of poverty. If these assertions are correct (and please remember that this is only speculation), you might expect to see a correlation of perhaps r = .50 between age and income as well as a correlation of r = .50 between income and moral development. These new correlations are displayed in Table 14.6. Notice that this table is similar to the preceding table in that all X variables display the same correlations with Y as were displayed earlier; age and moral development are still uncorrelated.

Table 14.6. Correlation Matrix: Nonzero Correlations among X Variables

	Variable	Y	X1	X2	X3
Y	Prosocial behavior	1.00
X1	Age	.30	1.00
X2	Income	.40	.50	1.00
X3	Moral development	.50	.00	.50	1.00

The X variables of Table 14.6 display the same correlations with Y as previously displayed in Table 14.5. Does this mean that the linear combination of the three X variables will still account for the same total percentage of variance in Y? In most cases, the answer is no. Remember that, with Table 14.5, the X variables were not correlated with one another whereas in Table 14.6, there is now a substantial correlation between age and income, and between income and moral development. These correlations can decrease the total variance in Y that is accounted for by the X variables. The reasons for this are illustrated in the Venn Diagram of Figure 14.5.

In Figure 14.5, the shaded area represents variance in income that is accounted for by age and moral development. The area with cross-hatching, on the other hand, represents variance in prosocial behavior that is accounted for by income.

Notice that each X variable individually still accounts for the same percentage of variance in prosocial behavior: age still accounts for 9%; income still accounts for 16%; and moral development still accounts for 25%. In this respect, Figure 14.5 is similar to Figure 14.4.

However, there is one important respect in which the two figures are different. Figure 14.5 shows that some of the X variables are now correlated with one another: the area of overlap between age and income (shaded with dots) indicates the fact that age and income now share about 25% of their variance in common (because the correlation between these variables was .50, and .50² = .25). In the same way, the area of overlap between income and moral development (also shaded) represents the fact that these variables share about 25% of their variance in common.

There is an important consequence of the fact that some of the X variables are now correlated with one another: some of the variance in Y that is accounted for by one X variable is now also accounted for by another X variable. For example, consider the X₂ variable, income. By itself, income accounted for 16% of the variance in prosocial behavior. But notice how the circle for age overlaps part of the variance in Y that is accounted for by income. (This area is shaded and cross-hatched.) This means that some of the variance in Y that is accounted for by income is also accounted for by age. In other words, because age and income are correlated, this has decreased the amount of variance in Y that is accounted for uniquely by income.

The same is true when one considers the correlation between income and moral development. The circle for moral development overlaps part of the variance in Y that is accounted for by income. (Again, this area is shaded and cross-hatched.) This shows that some of the variance in Y that was accounted for by income is now also accounted for by moral development.

In short, there is redundancy between age and income in the prediction of Y, and there is also some redundancy between income and moral development in the prediction of Y. The result of this correlation between the predictor variables is a net decrease in the total amount of variance in Y that is accounted for by the linear combination of X variables. Compare the Venn diagram for the situation in which the X variables were uncorrelated (Figure 14.4) to the Venn diagram in which there was some correlation among the X variables (Figure 14.5). When the X variables are not correlated among themselves, they account for 50% of the variance in Y. Now, notice the area in Y that overlaps with the X variables in Figure 14.5. The area of overlap is smaller in the second figure, showing that the X variables account for less of the total observed variance in Y when they are correlated with one another.

This is because X variables usually make a smaller unique contribution to the prediction of Y when they are correlated with one another. The greater the correlation among the X variables, the smaller the amount of unique variance in Y accounted for by each individual X variable, and hence the smaller the total variance in Y that is accounted for by the combination of X variables.

The meaning of unique variance can be understood with reference to the cross-hatched area in the Venn diagram of Figure 14.5. In the figure, the area that is both shaded and cross-hatched identifies the variance in Y that is accounted for by both income and age. Shading and cross-hatching are also used to identify the variance in Y accounted for by both income and moral development. The remaining variance in Y provided by income is the variance that is uniquely accounted for by income. In the figure, this is the area of overlap between income and prosocial behavior that is shaded in with only cross-hatching (not shading and cross-hatching). Obviously, this area is quite small, indicating that income accounts for very little variance in prosocial behavior that is not already accounted for by age and moral development.

There are several practical implications arising from this scenario. The first implication is that, in general, the amount of variance accounted for in a criterion variable will be larger to the extent that the following two conditions hold:

• The predictor variables demonstrate relatively strong correlations with the criterion variable.

• The predictor variables demonstrate relatively weak correlations with each other.

These conditions hold true “in general,” because they do not apply to the special case of a suppressor variable. (More on this in the following section.)

The second implication is that there generally is a point of diminishing returns when it comes to adding new X variables to a multiple regression equation. Because so many predictor variables in social science research are correlated, only the first few predictors added to a predictive equation are likely to account for meaningful amounts of unique variance in a criterion. Variables that are subsequently added will tend to account for smaller and smaller percentages of unique variance. At some point, predictors added to the equation will account for only negligible amounts of unique variance. For this reason, most multiple regression equations in social science research contain a relatively small number of variables, usually 2 to 10.

When Intercorrelated Predictors Do Include a Suppressor Variable

The preceding section describes the results that you can normally expect to observe when regressing a criterion variable on multiple intercorrelated predictor variables. However, there is a special case in which the preceding generalizations do not hold; that is the case of the suppressor variable. Although reports of genuine suppressor variables are somewhat rare in the social sciences, it is important that you understand the concept, so that you will recognize a suppressor variable when you encounter one.

Briefly, a suppressor variable is a predictor variable that improves the predictive power of a multiple regression equation by controlling for unwanted variation that it shares with other predictors in the equation. Suppressor variables typically display the following characteristics:

• zero or near-zero correlations with the criterion;

• moderate-to-strong correlations with at least one other predictor variable.

Suppressor variables are interesting because, even though they can display a bivariate correlation with the criterion variable of zero, adding them to a multiple regression equation can result in a meaningful increase in R² for the model. This of course, violates the generalizations drawn in the preceding section.

To understand how suppressor variables work, consider this fictitious example: imagine that you want to identify variables that can be used to predict the success of firefighters. To do this, you conduct a study with a group of 100 firefighters. For each participant, you obtain a “Firefighter Success Rating” that indicates how successful this person has been as a firefighter. These ratings are on a scale of 1 to 100, with higher ratings indicating greater success.

To identify variables that might be useful in predicting these success ratings, you have each firefighter complete a number of “paper-and-pencil” tests. One of these is a “Firefighter Knowledge Test.” High scores on this test indicate that the participant possesses the knowledge needed to operate a fire hydrant, enter a burning building safely, and perform other tasks related to firefighting. A second test is a “Verbal Ability Test.” This test has nothing to do with firefighting; high scores simply indicate that the participant has a good vocabulary and other verbal skills.

The three variables in this study could be represented with the following symbols:

Y	= Firefighter Success Ratings (the criterion variable);
XP	= Firefighter Knowledge Test (the predictor variable of interest);
XS	= Verbal Ability Test (the suppressor variable).

Imagine that you perform some analyses to understand the nature of the relationship among these three variables. First, you compute the Pearson correlation coefficient between the Firefighter Knowledge Test and the Verbal Ability Test, and find that r = .40. This is a moderately strong correlation (and it only makes sense that these two tests would be moderately correlated). This is because both firefighter knowledge and verbal ability are assessed by the same method: a paper-and-pencil questionnaire. To some extent, getting a high score on either of these tests requires that the participant be able to read instructions, read questions, read possible responses, and perform other verbal tasks. This means that the two tests are correlated because scores on both tests are influenced by participants’ verbal ability.

Next, you perform a series of regressions in which Firefighter Success Ratings (Y) is the criterion to determine how much of its variance is accounted for by various regression equations. This is what you learn:

• When the regression equation contains only the Verbal Ability Test, it accounts for 0% of the variance in Y.

• When the regression equation contains only the Firefighter Knowledge Test, it accounts for 20% of the variance in Y.

• When the regression equation contains both the Firefighter Knowledge Test and the Verbal Ability test, it accounts for 25% of the variance in Y.

The finding that the Verbal Ability Test accounts for none of the variance in Firefighter Success Ratings makes sense, because it (presumably) does not require a good vocabulary or other verbal skills to be a good firefighter.

The second finding that the Firefighter Knowledge Test accounts for a respectable 20% of the variance in Firefighter Success Ratings also makes sense as it is reasonable to expect more knowledgeable firefighters to be rated as better firefighters.

However, you run into a difficulty when trying to make sense of the third finding: that the equation that contains both the Verbal Ability Test and the Firefighter Knowledge Test accounts for 25% of observed variance in Y. How is it possible that the combination of these two variables accounts for 25% of the variance in Y when one accounted for only 20% and the other accounted for 0%?

The answer is that, in this situation, the Verbal Ability Test is serving as a suppressor variable. It is suppressing irrelevant variance in scores on the Firefighter Knowledge Test, thus “purifying” the relationship between the Firefighter Knowledge Test and Y. Here is how it works. Scores on the Firefighter Knowledge Test are influenced by at least two factors: their actual knowledge about firefighting; and their verbal ability (e.g., ability to read instructions). Obviously, the first of these two factors is relevant for predicting Y whereas the second factor is not. Because scores on the Firefighter Knowledge Test are to some extent “contaminated” by the effects of participants’ verbal ability, the actual correlation between the Firefighter Knowledge Test and Firefighter Success Ratings is somewhat lower than it would be if you could somehow purify Knowledge Test scores of this unwanted verbal factor. That is exactly what a suppressor variable does.

In most cases, a suppressor variable is given a negative regression weight in a multiple regression equation. (These weights will be discussed in more detail later in this chapter.) Partly because of this, including the suppressor variable in the equation adjusts each participant’s predicted score on Y so that it comes closer to that participant’s actual score on Y. In the present case, this means that, if a participant scores above the mean on the Verbal Ability Test, his or her predicted score on Y will be adjusted downward to penalize for scoring high on this irrelevant predictor. Alternatively, if a participant scores below the mean on the Verbal Ability Test, his or her predicted score on Y will be adjusted upward. Another way of thinking about this is to say that a person applying to be a firefighter who has a high score on the Firefighter’s Knowledge Test but a low score on the Verbal Ability Test would be preferred over an applicant with a high score on the Knowledge Test and a high score on the Verbal Test. (This is because the second candidate’s score on the Knowledge Test was probably inflated due to his or her good verbal skills.)

The net effect of these corrections is improved accuracy in predicting Y. This is why you earlier found that R² is .25 for the equation that contains the suppressor variable, but only .20 for the equation that does not contain it.

The possible existence of suppressor variables has implications for multiple regression analyses. For example, when attempting to identify variables that would make good predictors in a multiple regression equation, it is clear that you should not base the selection exclusively on the bivariate (Pearson) correlations between the variables. For example, even if two predictor variable are moderately or strongly correlated, it does not necessarily mean that they are always providing redundant information. If one of them is a suppressor variable, then the two variables are not entirely redundant. (That noted, predictor variables with coefficients greater than r = |.89| create computational problems and should be avoided. See the description of multicollinearity in final section of this chapter, “Assumptions Underlying Multiple Regression.”)

In the same way, a predictor variable should not be eliminated from consideration as a possible predictor just because it displays a low bivariate correlation with the criterion. This is because a suppressor variable might display a bivariate correlation with Y of zero, even though it could substantially increase R² if added to a multiple regression equation. When starting with a set of possible predictor variables, it is generally safer to begin the analysis with a multiple regression equation that contains all predictors, on the chance that one of them serves as a suppressor variable. (The topic of choosing an “optimal” subset of predictor variables from a larger set is a complex one that is beyond the scope of this book.)

To provide some sense of perspective, however, you should take comfort in the knowledge that true suppressor variables are somewhat rare in social science research. In most cases, you can expect your data to behave according to the generalizations made in the preceding section (dealing with regression equations that do not contain suppressors). That is, in most cases, you will find that R² is larger to the extent that the X variables are more strongly correlated with Y and less strongly correlated with one another. To learn more about suppressor variables, see Pedhazur (1982).

The Uniqueness Index

A uniqueness index represents the percentage of variance in a criterion that is accounted for by a given predictor variable, above and beyond the variance accounted for by the other predictor variables in the equation. A uniqueness index is one measure of an X variable’s importance as a predictor: the greater the amount of unique variance accounted for by a predictor, the greater its usefulness.

The concept of a uniqueness index can be illustrated with reference to Figure 14.6 that illustrates the uniqueness index for the predictor variable, income. Figure 14.6 is identical to Figure 14.5 with respect to the correlations between income and prosocial behavior and the correlations among the three X variables. In Figure 14.6, however, only the area that represents the uniqueness index for income is shaded. It can be seen that this area is consistent with the previous definition which states that the uniqueness index for a given variable represents the percentage of variance in the criterion (prosocial behavior) that is accounted for by the predictor variable (income) over and above the variance accounted for by the other predictors in the equation (i.e., age and moral development).

When performing multiple regression, it is often useful to compute the uniqueness index for each X variable in the equation. These indices, along with other information, can aid understanding of the nature of the relationship between the criterion and the predictor variables.

Computing the uniqueness index for a given X variable actually requires estimating two multiple regression equations. The first equation should include all of the X variables of interest. This can be referred to as the full equation because it contains the full set of predictors.

In contrast, the second multiple regression equation should include all of the X variables except for the X variable of interest. For this reason, this second equation can be called the reduced equation.

To calculate the uniqueness index for the X variable of interest, subtract the R² value for the reduced equation from the R² value for the full equation. The resulting difference is the uniqueness index for the X variable of interest.

This procedure can be illustrated by calculating the uniqueness index for income. Assume that two multiple regression equations are computed and that prosocial behavior is the criterion variable for both. With the full equation, the predictor variables include age, income, and moral development. With reduced equation, the predictors include only age and moral development. (Income was dropped because you wish to calculate the uniqueness index for income.) Assume that the following R² values are obtained for the two equations:

R2Full	= .40
R2Reduced	= .35

These R² values show that, when all three predictor variables were included in the equation, they accounted for 40% of the variance in prosocial behavior. However, when income was dropped from this equation, the reduced equation accounted for only 35% of the variance in prosocial behavior. The uniqueness index for income (symbolized as U) can now be calculated by subtracting the reduced-equation R² from the full-equation R²:

U =	R2Full	– R2Reduced
U =	.40	– .35
U =	.05

The uniqueness index for income is .05, meaning that income accounts for only 5% of the variance in prosocial behavior, beyond the variance accounted for by age and moral development.

To compute the uniqueness index for age, you would have to estimate yet another multiple regression equation: one in which age is dropped from the full equation (i.e., an equation containing only income and moral development). The R² for the new reduced equation is calculated and is subtracted from the R² for the full equation to arrive at the U for age. A similar procedure then is performed to compute the U for moral development. A later section of this chapter (“Computing Uniqueness Indices with PROC REG”) describes how the results of SAS’ REG procedure can be used to compute uniqueness indices for a set of predictors.

Testing the Significance of the Difference between Two R² Values

The preceding section shows that you can calculate a uniqueness index by

• estimating two R² values: one for a full equation with all X variables included and one for a reduced equation with all X variables except for the X variable of interest;

• subtracting the R² for the reduced model from the R² for the full model.

The difference between the two R² values is the uniqueness index for the dropped X variable.

Once a uniqueness index is calculated, however, the next logical question is, “Is this uniqueness index significantly different from zero?” In other words, does the predictor variable represented by this index account for a significant amount of variance in the criterion beyond the variance accounted for by the other predictors? To answer this question, it is necessary to test the significance of the difference between the R² value for the full equation versus the R² for the reduced equation. This section shows how this is done.

One of the most important procedures in multiple regression analysis involves testing the significance of the difference between R² values. This test is conducted when you have estimated two multiple regression equations, and want to know whether the R² value for one equation is significantly larger than the R² for the other equation.

There is one important condition when performing this test, however: The two multiple regression equations must be nested. Two equations are said to be nested when they include the same criterion variable and the X variables included in the smaller equation are a subset of the X variables included in the larger equation.

To illustrate this concept, we refer again to the study in which

Y	= Prosocial behavior
X1	= Age
X2	= Income
X3	= Moral development

The following two multiple regression equations are nested:

Full equation:	Y = X1 + X2 + X3
Reduced equation:	Y = X1 + X2

It can be said that the reduced equation is nested within the full equation because the predictors for the reduced equation (X₁ and X₂) are a subset of the predictors in the full equation (X₁, X₂, and X₃).

In contrast, the following two multiple regression equations are not nested:

Full equation:	Y = X1 + X2 + X3
Reduced equation:	Y = X1 + X4

Even though the “reduced” equation in the preceding example contains fewer X variables than the “full” equation, it is not nested within the full equation. This is because the reduced equation contains the variable X₄, which does not appear in the full equation. The X variables of the reduced equation are, therefore, not a subset of the X variables in the full equation.

When two equations are nested, it is possible to test the significance of the difference between the R² values for the equations. This is sometimes referred to as “testing the significance of variables added to the equation.” To understand this expression, think about a situation in which the full equation contains X₁, X₂, and X₃, and the reduced equation contains only X₁ and X₂. The only difference between these two equations is the fact that the full equation contains X₃ while the reduced equation does not. By testing the significance of the difference between the R² values for the two equations, you are determining whether adding X₃ to the reduced equation results in a significant increase in R².

Here is the equation for the F ratio that tests the significance of the difference between two R² values:

where

R2Full	=	the obtained value of R2 for the full multiple regression equation (i.e., the equation containing the larger number of predictor variables)
R2Reduced	=	the obtained value of R2 for the reduced multiple regression equation (i.e., the equation containing the smaller number of predictor variables)
KFull	=	the number of predictor variables in the full multiple regression equation
KReduced	=	the number of predictor variables in the reduced multiple regression equation
N	=	the total number of participants in the sample

The preceding equation can be used to test the significance of any number of variables added to a regression equation. The examples in this section involve testing the significance of adding just one variable to an equation. This section focuses on the one-variable situation because of its relevance to the concept of the uniqueness index, as previously discussed. Remember that a uniqueness index represents the percentage of variance in a criterion that is accounted for by a single X variable over and above the variance accounted for by the other X variables. Earlier, it was stated that a uniqueness index is calculated by estimating a full equation with all X variables, along with a reduced equation in which one X variable has been deleted. The difference between the two resulting R² values is the uniqueness index for the deleted X variable.

The relevance of the preceding formula to the concept of the uniqueness index should now be evident. This formula allows you to test the statistical significance of a uniqueness index. It allows you to test the statistical significance of the variance in Y accounted for by a given X variable beyond the variance accounted for by other X variables. For this reason, the formula is helpful in determining which predictors are relatively important and which are comparatively unimportant.

To illustrate the formula, imagine that you conduct a study in which you use age, income, and moral development to predict prosocial behavior in a sample of 104 participants. You now want to calculate the uniqueness index for the predictor, moral development. To do this, you estimate two multiple regression equations: a “full model” that includes all three X variables as predictors and a “reduced model” that includes all predictors except for moral development. Here are the R² values obtained for the two models:

Table 14.7. Variance Accounted for by Full and Reduced Models, Prosocial Behavior Study

	R2 Obtained for this model	Predictor variables included in the equation
	.30	Age, income, moral development (full model)
	.20	Age, income (reduced model)
Note: N = 104.

The preceding table shows that the reduced equation (including only age and income) accounts for only 20% of the variance in prosocial behavior. Adding moral development to this equation, however, increases R² to .30. The uniqueness index for moral development is therefore .30 – .20 or .10.

To compute the F test that tests the significance of the difference between these two R² values, insert the appropriate figures in the following equation:

The F ratio for this test is 14.29. To determine whether this F is significant, you turn to the table of critical values of F in Appendix C. To find the appropriate critical value of F, it is necessary to first establish the degrees of freedom for the numerator and the degrees of freedom for the denominator that are associated with the current analysis.

When comparing the significance of the difference between two R² values, the degrees of freedom for the numerator are equal to K_Full – K_Reduced (which appears in the numerator of the preceding equation). In the present analysis, the number of predictors in the full equation is 3, and the number in the reduced equation is 2; therefore, the degrees of freedom (df) for the numerator is 3 – 2 or 1.

The degrees of freedom for the denominator of this F test is N – K_Full –1 (which appears in the denominator of the preceding equation). The sample size in the present study was 104, so the degrees of freedom for the denominator is 104 – 3 –1 = 100.

The table of F values shows that, with 1 df for the numerator and 100 df for the denominator, the critical value of F is approximately 3.94 (p<.05). The preceding formula produced an observed F value of 14.29, which of course is much larger than this critical value. You can therefore reject the null hypothesis of no difference and conclude that there is a significant difference between the two R² values. In other words, adding moral development to an equation already containing age and income results in a significant increase in observed variance in prosocial behavior. Therefore, the uniqueness index for moral development is proven to be statistically significant.

Multiple Regression Coefficients

The b weights discussed earlier in this chapter were referred to as nonstandardized multiple regression coefficients. It was said that a multiple regression coefficient for a given X variable represents the average change in Y that is associated with a one-unit change in that X variable while holding constant the remaining X variables. “Holding constant” means that the multiple regression coefficient for a given predictor variable is an estimate of the average change in Y that would be associated with a one-unit change in that X variable if all participants had identical scores on the remaining X variables.

When conducting multiple regression analyses, researchers often seek to determine which of the X variables are relatively important predictors of the criterion, and which are relatively unimportant. By doing this, you might be tempted to review the multiple regression coefficients estimated in the analysis and use these as indicators of importance. According to this logic, a regression coefficient represents the amount of weight that is given to a given X variable in the prediction of Y. If a variable is given much weight, it must be an important predictor.

Nonstandardized versus Standardized Coefficients

However, considerable caution must be exercised when using multiple regression coefficients in this manner for at least two reasons. First, you must remember that two types of multiple regression coefficients are produced in the course of an analysis: nonstandardized coefficients and standardized coefficients. Nonstandardized multiple regression coefficients (sometimes called b weights and symbolized with a lowercase letter b) are the coefficients that are produced when the data analyzed are in raw score form. “Raw score” form means that the variables have not been standardized in any way: the different variables might have very different means and standard deviations. For example, the standard deviation for X₁ can be 1.35, while the standard deviation for X₂ can be 584.20.

Generally speaking, it is not appropriate to use the relative size of nonstandardized regression coefficients in assessing the relative importance of predictor variables. This is because the relative size of a nonstandardized coefficient for a given predictor variable is influenced by the size of that predictor’s standard deviation. Other things being equal, the variables with larger standard deviations tend to have smaller nonstandardized regression coefficients while variables with smaller standard deviations tend to have larger regression coefficients. Therefore, the size of nonstandardized coefficients generally indicates nothing about the relatively important predictor variables.

If this is the case, then what are the nonstandardized coefficients useful for? They are most frequently used to calculate participants’ predicted scores on Y. For example, an earlier section presented a multiple regression equation for the prediction of prosocial behavior in which X₁ = age, X₂ = income, and X₃ = moral development. That equation is reproduced here:

Y′ = (.10) X₁ + (.25) X₂ + (1.10) X₃ + (-3.25)

In this equation, the nonstandardized multiple regression coefficient for X₁ is .10, the coefficient for X₂ is .25, and so forth. If you had a participant’s raw scores on the three predictor variables, these values could be inserted in the preceding formula to compute that participant’s estimated score on Y. The resulting Y′ value would also be in raw score form. It would be an estimate of the number of prosocial acts you expect the participant to perform over a six-month period.

In summary, you should not refer to the nonstandardized regression coefficients to assess the relative importance of predictor variables. A better alternative (though still not perfect) is to refer to the standardized coefficients. Standardized multiple regression coefficients (sometimes called beta weights and symbolized by the Greek letter β) are the coefficients that would be produced if the data analyzed were in standard score form. “Standard score” form (or “z score form”) means that the variables are standardized so that each has a mean of zero and a standard deviation of 1. This is important because all variables (Y variables and X variables alike) now have the same standard deviation (i.e., a standard deviation of 1); they are now measured on the same scale of magnitude or metric. You no longer have to worry that some variables display large regression coefficients simply because they have small standard deviations. To some extent, the size of standardized regression coefficients does reflect the relative importance of the various predictor variables; these coefficients should therefore be among the results that are consulted when interpreting the results of a multiple regression analysis.

For example, assume that the analysis of the prosocial behavior study produces the following multiple regression equation with standardized coefficients:

Y′ = (.70) X₁ + (.20) X₂ + (.20) X₃

In the preceding equation, X₁ displays the largest standardized coefficient. This could be interpreted as evidence that it is a relatively important predictor variable compared to X₂ and X₃.

You can see that the preceding equation, like all regression equations with standardized coefficients, does not contain an intercept constant. This is because the intercept is always equal to zero in a standardized equation. This is a useful fact to know; if a researcher has presented a multiple regression equation in a research article but has not indicated whether it is a standardized or a nonstandardized equation, look for the intercept constant. If an intercept is included in the equation, it is almost certainly a nonstandardized equation. If there is no intercept, it is probably a standardized equation. Remember also that the lowercase letter b is typically used to represent nonstandardized regression coefficients, whereas the Greek letter β is used to represent standardized coefficients.

The Reliability of Multiple Regression Coefficients

The preceding section notes that standardized coefficients reflect the importance of predictors only to some extent. This qualification is necessary because of the unreliability that is often demonstrated by multiple regression weights. In this case, unreliability refers to the fact that, when multiple regression using the same variables is performed on data from more than one sample, very different estimates of the multiple regression coefficients are often obtained with the different samples. This is the case for standardized as well as nonstandardized coefficients.

For example, assume that you recruit a sample of 50 participants, measure the variables discussed in the preceding section (prosocial behavior, age, income, moral development), and compute a multiple regression equation in which prosocial behavior is the criterion and the remaining variables are predictors (assume that age, income, and moral development are X₁, X₂, and X₃, respectively). With the analysis completed, it is possible that your output would reveal the following standardized regression coefficients for the three predictors:

Y′ = (.70) X₁ + (.20) X₂ + (.20) X₃

The relative size of the coefficients in the preceding equation suggests that X₁ (with a beta weight of .70) is the most important predictor of Y, while X₂ and X₃ (each with beta weights of .20) are much less important.

However, what if you were then to attempt to replicate your study with a different group of 50 participants? It is unfortunately possible (if not likely) that would obtain very different beta weights for the X variables. For example, you might obtain the following:

Y′ = (.30) X₁ + (.50) X₂ + (.10) X₃

In the second equation, X₂ has emerged as the most important predictor of Y, followed by X₁ and X₃.

This is what is meant by the unreliability of standardized regression coefficients. When the same study is performed on different samples, researchers sometimes obtain coefficients of very different sizes. This means that the interpretation of these coefficients must always be made with caution.

This problem of unreliability is more likely in some situations than in others. Specifically, multiple regression coefficients become increasingly unreliable as the analysis is based on increasingly smaller samples and as the X variables become increasingly correlated with one another. Unfortunately, much of the research that is carried out in the social sciences involves the use of small samples and correlated X variables. For this reason, the standardized regression coefficients (i.e., beta weights) are only some of the pieces of information that should be reviewed when assessing the relative importance of predictor variables. The use of these coefficients should be supplemented with a review of the simple bivariate correlations between the X variables and Y and the uniqueness indices for the X variables. The following sections show how to do this.