1.6. Selection and Adjustment of Grain-Sizes
The ability to select a proper grain-size world for a given problem is fundamental to human intelligence and flexibility. The ability enables us to map the complex world around us into a simple one that is computationally tractable. At the same time, the attributes in question of the world are still preserved. As mentioned before, it is not necessarily true that any classification can achieve the goal.
How to select a proper grain-size is a domain-dependent problem mainly. We'll discuss some general principles below via semi-order spaces.
It has been shown that the compatibility of R and T is the foundation for assuring that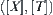 
is also a semi-order space. We will discuss below how to adjust R such that it is compatible with T.
is also a semi-order space. We will discuss below how to adjust R such that it is compatible with T.1.6.1. Mergence Methods
Assume that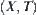 
is a semi-order space, where X is a finite set, R is an equivalence relation on X and is incompatible with T. 
is a quotient space corresponding to R. We will discuss how to adjust R by mergence methods.
is a semi-order space, where X is a finite set, R is an equivalence relation on X and is incompatible with T. 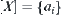is a quotient space corresponding to R. We will discuss how to adjust R by mergence methods.We define a new partition 
, where ‘<’ is a topology 
on 
induced from T. Obviously, 
is a partition of X. Let 
be an equivalence relation corresponding to partition 
.
, where ‘<’ is a topology 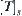on 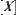induced from T. Obviously, 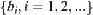is a partition of X. Let 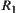be an equivalence relation corresponding to partition 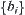.Proposition 1.9
defined above is compatible with T. If an equivalence relation 
satisfies (1) and T are compatible, (2) if 
, then 
, i.e., is the finest one, where 
if 
, then 
.Proof:
on is a right-order topology induced from T. [X] is a quotient space corresponding to R. 
is a quotient topology on [X]. 
and 
are quotient spaces corresponding to and , respectively.For 
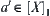, if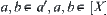 
, from the definitions of 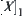and , we have 
, i.e., any neighborhood of a must contain b and is also the neighborhood of b. Conversely, any neighborhood of b must contain a and is also the neighborhood of a. Thus, the neighborhood systems of a and b are the same. Their common neighborhood system is just the neighborhood system of a′ on . In other words, if elements on [X] having a common neighborhood system are classified as one category, then [X] is revised as .
, if , from the definitions of and 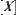, we have 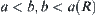, i.e., any neighborhood of a must contain b and is also the neighborhood of b. Conversely, any neighborhood of b must contain a and is also the neighborhood of a. Thus, the neighborhood systems of a and b are the same. Their common neighborhood system is just the neighborhood system of a′ on 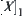. In other words, if elements on [X] having a common neighborhood system are classified as one category, then [X] is revised as 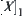.Now we prove that 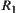is compatible. Assuming 
and 
, from the above discussion, 
and 
on have a common neighborhood system. 
, 
, a and b have a common neighborhood system. From the definition of , a and b belong to the same category on . Thus, 
, i.e., is compatible.
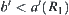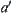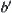is compatible. Assuming and , from the above discussion, and on 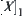have a common neighborhood system. , , 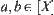a and b have a common neighborhood system. From the definition of 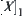, a and b belong to the same category on 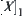. Thus, 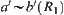, i.e., 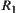is compatible.Finally, we prove that 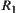is the finest one. Assume that is any partition and .
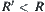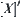is the finest one. Assume that is any partition and .We will prove below that . Let be a quotient space corresponding to and its projection be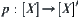 
. For 
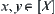and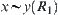 
, let 
, 
.
. Let be a quotient space corresponding to and its projection be . For and , let 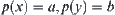, 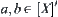.Assume that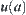 
is any neighborhood of 
on . Since , regarding as a set on , it is open, i.e., 
is open on . Since 
, 
, i.e., is a neighborhood of x. On the other hand, since , x and y have the same neighborhood system, i.e., is also a neighborhood of y. Thus, 
. We have 
, i.e., 
.
is any neighborhood of on 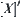. Since 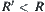, regarding 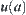as a set on 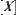, it is open, i.e., 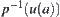is open on 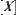. Since 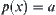, , 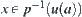i.e., 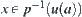is a neighborhood of x. On the other hand, since 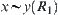, x and y have the same neighborhood system, i.e., 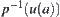is also a neighborhood of y. Thus, 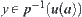. We have 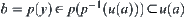, i.e., 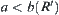.Similarly,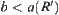 
, i.e., 
.
, i.e., 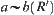.Finally, .
...................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.