2.2. The Estimation of Computational Complexity
The aim of this section is to estimate the computational complexity, based on the mathematical model presented in Chapter 1, when the multi-granular computing is used (Zhang and Zhang, 1990d, 1992).
2.2.1. The Assumptions
A problem space is assumed to be a finite set. Symbol 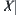 denotes the number of elements in X. Sometimes, we simply use X instead of
denotes the number of elements in X. Sometimes, we simply use X instead of 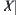 if no confusion is made.
if no confusion is made.
If we solve the problem X directly, i.e., finding a goal in X, the computational complexity is assumed to be 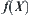 . Then, the complexity will be changed to
. Then, the complexity will be changed to 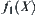 by using the multi-granular computing. Now, the point is in what conditions that we may have the result
by using the multi-granular computing. Now, the point is in what conditions that we may have the result 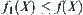 .
.
Before the discussion, we make the following assumption for 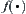 .
.
Hypothesis A
Assume that 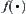 only depends on the number of elements in X, and independent of its structure, or other attributes. Both domain and range of
only depends on the number of elements in X, and independent of its structure, or other attributes. Both domain and range of 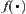 are assumed to be
are assumed to be 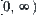 , i.e., a non-negative real number. Namely,
, i.e., a non-negative real number. Namely,
(1)  is a monotonically increasing function on
is a monotonically increasing function on  .
.
(2)  , we have
, we have 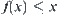 .
.
Now, we solve X by using the multi-granular computing strategy. That is, X is classified with respect to 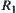 . Its corresponding quotient space is denoted by
. Its corresponding quotient space is denoted by 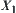 . Then the original problem on X is converted into the corresponding problem on
. Then the original problem on X is converted into the corresponding problem on 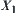 . Since some information will lose on
. Since some information will lose on 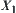 due to the abstraction, generally, we can't find the goal of X directly from its quotient space
due to the abstraction, generally, we can't find the goal of X directly from its quotient space 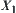 . Instead, we can only have a useful clue to the final solution of X from
. Instead, we can only have a useful clue to the final solution of X from 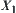 . Thus, in order to describe the relation between the results obtained from the quotient and its original spaces, we introduce a new function as follows.
. Thus, in order to describe the relation between the results obtained from the quotient and its original spaces, we introduce a new function as follows.
Definition 2.1
Assume that 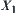 is a quotient space of X and f is a complexity function of X. Suppose that the complexity function of
is a quotient space of X and f is a complexity function of X. Suppose that the complexity function of 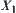 is less than
is less than 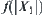 and the number of elements which might contain the goal is estimated at g at most. Define a goal estimation function
and the number of elements which might contain the goal is estimated at g at most. Define a goal estimation function 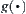 as follows:
as follows:
![]()
Assume that 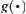 is a monotonically increasing function and
is a monotonically increasing function and 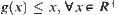 .
.
We have a sequence 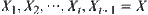 of quotient spaces with t levels, where
of quotient spaces with t levels, where 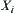 is a quotient space of
is a quotient space of 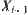 ,
, 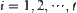 . After the multi-granular computing with t levels, the total complexity function is assumed to be
. After the multi-granular computing with t levels, the total complexity function is assumed to be 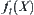 . We next estimate the
. We next estimate the 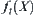 .
.
2.2.2. The Estimation of the Complexity Under Deterministic Models
Our goal is to estimate the asymptotic property of complexity function under the multi-granular computing. For simplicity, let 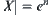 , i.e., X has
, i.e., X has 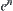 elements. The other variables are limited to the order of
elements. The other variables are limited to the order of 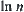 ,
, 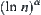 , and
, and 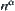 , where
, where 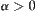 .
.
Local Partition Method
Definition 2.2
Assume 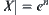 . The complexity function
. The complexity function 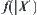 is called divergent if for any given b > 0, have
is called divergent if for any given b > 0, have 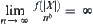 .
.
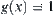 Case
Case
Suppose that 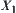 is a quotient space of X. We seek the goal of X from
is a quotient space of X. We seek the goal of X from 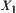 . When solving the problem on
. When solving the problem on 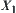 , the computational complexity only depends on the number of elements in
, the computational complexity only depends on the number of elements in 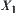 . After the amount
. After the amount 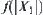 of computation, we find element
of computation, we find element 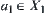 which might contain the goal. Due to
which might contain the goal. Due to 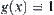 , there is only one such element,
, there is only one such element, 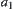 . Again, assume that each equivalence class has the same number of elements.
. Again, assume that each equivalence class has the same number of elements.
Then, we seek the goal within the equivalence class 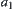 (
(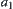 is an element in X1) in X.
is an element in X1) in X.
When  , from
, from 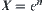 we have
we have 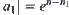 . Thus, the total computational complexity for solving X by the multi-granular computing with two levels is
. Thus, the total computational complexity for solving X by the multi-granular computing with two levels is
![]() (2.1)
(2.1)
Regarding 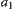 as a set of X, if set
as a set of X, if set 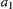 is too large, then
is too large, then 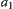 is further partitioned. Assume that
is further partitioned. Assume that 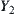 is a quotient set of set
is a quotient set of set 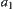 and
and 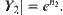 The total complexity for solving X by the multi-granular computing with three levels is
The total complexity for solving X by the multi-granular computing with three levels is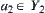 is an element of
is an element of 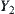 which might contain the goal.
which might contain the goal.
![]() (2.2)
(2.2)
From induction, the total complexity for solving X by the multi-granular computing with t levels is
![]() (2.3)
(2.3)
![]()
If in each level, its elements are classified into c equivalence classes without exception, where 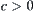 is an integer, i.e.,
is an integer, i.e., 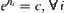 . Since
. Since 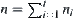 , we have
, we have 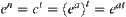 , where
, where 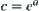 . Then, we have
. Then, we have 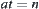 ,
, 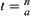 . Substituting
. Substituting 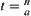 into (2.3), we have
into (2.3), we have 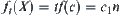 , i.e.,
, i.e., 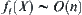 .
.
We have the following proposition.
Proposition 2.1
If a unique element which contains the goal can be found at each granular level, i.e., 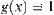 , there exists a hierarchical partition method for X such that X can be solved in a linear time (
, there exists a hierarchical partition method for X such that X can be solved in a linear time (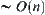 ), in spite of the form of complexity function f(X) (f(X) might be divergent).
), in spite of the form of complexity function f(X) (f(X) might be divergent).
Example 2.4
We are given 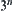 coins, one of which is known to be lighter than the rest. Using a two-pan scale, we must find the counterfeit coin as soon as possible.
coins, one of which is known to be lighter than the rest. Using a two-pan scale, we must find the counterfeit coin as soon as possible.
To solve the problem, we may weigh a pair of coins (one in each pan) at a time. That is, we find the counterfeit one from 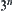 coins directly. The mean computational complexity, the average number of weighing, is
coins directly. The mean computational complexity, the average number of weighing, is 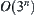 . By the multi-granular computing,
. By the multi-granular computing, 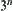 coins may first be divided into three groups equally. Then a quotient space
coins may first be divided into three groups equally. Then a quotient space 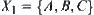 is gained. Obviously, we can find which group will contain the counterfeit coin in one test. That is, by weighing A and B, the suspect will be in C in case the scale balances, the suspect will be in either A or B (the lighter one) in case the scale tips. In our terminology, in the first weighting,
is gained. Obviously, we can find which group will contain the counterfeit coin in one test. That is, by weighing A and B, the suspect will be in C in case the scale balances, the suspect will be in either A or B (the lighter one) in case the scale tips. In our terminology, in the first weighting, 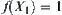 and
and 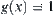 .
.
The same procedure can be used for the suspect class, the outcome of the first weighting. The same process continues until the counterfeit coin is found. From (2.3) by letting 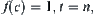 we have
we have 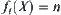 . That is, the counterfeit coin can be found in n tests.
. That is, the counterfeit coin can be found in n tests.
Proposition 2.2
(1) when 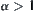 ,
, 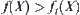 ,
,
(2) when 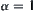 ,
, 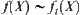 ,
,
(3) when 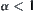 ,
, 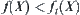 .
.
From Proposition 2.1, the proposition is obtained directly.
The proposition indicates that as long as the complexity f(X) is greater than a linearly growing function, it can be reduced by the multi-granular computing:
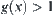 case
case
Quotient space 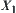 is obtained after partitioning X. Through the amount
is obtained after partitioning X. Through the amount 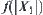 of computation, it is found that
of computation, it is found that 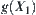 elements in
elements in 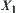 might contain the goal of X. These elements are assumed to be
might contain the goal of X. These elements are assumed to be 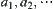 . The total complexity for solving X by the multi-granular computing with two levels is
. The total complexity for solving X by the multi-granular computing with two levels is
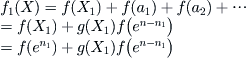
Each 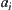 is partitioned. The corresponding quotient space is denoted by
is partitioned. The corresponding quotient space is denoted by 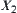 ,
, 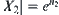 . The complexity for solving X by the multi-granular computing with three levels is:
. The complexity for solving X by the multi-granular computing with three levels is:
![]()
From induction, the total complexity for solving X by the multi-granular computing with t levels is: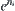 is the number of elements in the i-th granular level (abstraction level),
is the number of elements in the i-th granular level (abstraction level), 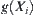 is the goal estimation function on
is the goal estimation function on 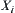 .
.
![]() (2.4)
(2.4)
From (2.4), we estimate the order of 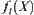 . If
. If  , we have
, we have
(1) If 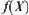 is divergent, for any t, then
is divergent, for any t, then 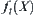 must be divergent;
must be divergent;
(2) If 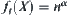 , letting
, letting 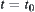 (constant), then
(constant), then 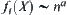 ;
;
(3) If 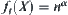 , letting
, letting 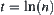 , then
, then 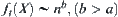 ;
;
(4) If 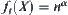 , letting
, letting 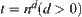 , then
, then 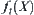 is divergent.
is divergent.
We only give the proof of case (3) below.
From the results above, we have the following proposition.
Proposition 2.3
If  , based on the above partition model, we cannot reduce the asymptotic property of the complexity for solving X by the multi-granular computing paradigm. The result is disappointing. It is just the partitioning strategy we adopted that leads to the result. Based on the above strategy, in the first granular level if elements
, based on the above partition model, we cannot reduce the asymptotic property of the complexity for solving X by the multi-granular computing paradigm. The result is disappointing. It is just the partitioning strategy we adopted that leads to the result. Based on the above strategy, in the first granular level if elements 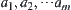 are suspected of containing the goal, then each
are suspected of containing the goal, then each 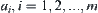 , is further partitioned, respectively. Assume that each
, is further partitioned, respectively. Assume that each 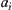 still has m suspects. The process goes on, after n granular levels (abstraction levels), we will have
still has m suspects. The process goes on, after n granular levels (abstraction levels), we will have 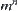 suspects, so the divergence happens. This partitioning method is called local partition.
suspects, so the divergence happens. This partitioning method is called local partition.
In order to overcome the shortage of local partition, the second alternative can be adopted. When 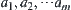 are found to be suspects, all
are found to be suspects, all 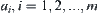 , are merged into one equivalence class a. Then, we partition the whole merged class a rather than each
, are merged into one equivalence class a. Then, we partition the whole merged class a rather than each 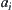 . This strategy is called global partition.
. This strategy is called global partition.
Global Partition Method
Assume that in a granular level there exist 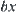 elements that are suspected of containing the goal, where x is the total number of elements in that level. That is,
elements that are suspected of containing the goal, where x is the total number of elements in that level. That is, 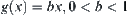 .
.
Suppose that X is partitioned with respect to R. Its corresponding quotient space is 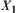 . Letting
. Letting 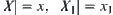 , we have the complexity function:
, we have the complexity function:
![]()
Here each equivalence class in 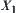 is supposed to have the same number of elements of X.
is supposed to have the same number of elements of X.
Now, by partitioning 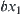 elements, i.e., all suspects in X1, we have a quotient space X2. Letting
elements, i.e., all suspects in X1, we have a quotient space X2. Letting 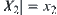 , we have
, we have
![]()
From induction, it follows that
![]() (2.6)
(2.6)
When 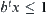 , the goal is found.
, the goal is found.
Suppose that 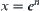 . By letting
. By letting 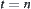 , we have
, we have 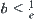 , i.e.,
, i.e., 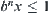 .
.
Generally, letting 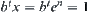 , we have
, we have 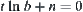 .
.
Since 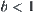 , we have
, we have 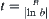 .
.
We have the following proposition.
Proposition 2.4
If we can have 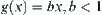 , by the global partition method, when
, by the global partition method, when 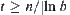 , then the complexity for solving X is
, then the complexity for solving X is 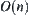 regardless of whether the original complexity function
regardless of whether the original complexity function 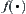 is divergent or not.
is divergent or not.
The proposition shows that different partition strategies may have different results. So long as in each granular level there is enough information such that 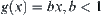 , then when
, then when 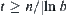 , the linear complexity can be reached by the global partition method. In the following example, since
, the linear complexity can be reached by the global partition method. In the following example, since 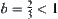 , from Proposition 2.4, it is known that so long as
, from Proposition 2.4, it is known that so long as 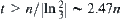 , we can get the linear complexity.
, we can get the linear complexity.
Example 2.5
We are given 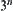 coins, one of which is known to be heavier or lighter than the rest. Using a two-pan scale, we must find the counterfeit coin and determine whether it is light or heavy as soon as possible.
coins, one of which is known to be heavier or lighter than the rest. Using a two-pan scale, we must find the counterfeit coin and determine whether it is light or heavy as soon as possible.
First, coins are divided into three groups (A, B, C) equally. By weighing A and B (one in each pan), the suspect will be in C in case the scale balances, the suspect will be in A or B in case the scale tips.
In terms of our quotient space model, we have
![]()
From Proposition 2.4, so long as the number t of granular levels is greater than 2.47n, the counterfeit coin can be found.
In fact, it can be proved that the counterfeit coin may be found from 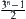 coins in n tests.
coins in n tests.
It is shown that the computational complexity by the multi-granular computing also depends on the way in which the domain X is partitioned.
2.2.3. The Estimation of the Complexity Under Probabilistic Models
In the previous section, two partition methods are given. One is to partition each class that might contain the goal. It is called the local partition method. The method requires that only the unique element that might contain the goal is identified at each partition so that the computational complexity can be reduced. The other one is to partition the whole set of classes that might contain the goal. This is called the global partition method. In order to reduce the complexity by the method, 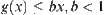 must be satisfied at each partition. These results are unsatisfactory. So we need a more reasonable model, i.e., probabilistic models.
must be satisfied at each partition. These results are unsatisfactory. So we need a more reasonable model, i.e., probabilistic models.
From Definition 2.1, it's known that goal estimation function 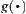 is:
is:
![]()
If 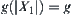 , it means that the number of elements in X1 which might contain the goal is g at most. Generally, it is not the case that each element contains the goal with the same probability. Thus, it can reasonably be described by probabilistic models.
, it means that the number of elements in X1 which might contain the goal is g at most. Generally, it is not the case that each element contains the goal with the same probability. Thus, it can reasonably be described by probabilistic models.
Definition 2.3
Assume that 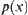 is a probabilistic distribution function that exactly x elements of set A might contain the goal. Let
is a probabilistic distribution function that exactly x elements of set A might contain the goal. Let 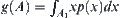 , where
, where 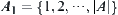 . Then,
. Then, 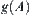 is a goal estimation function under the statistical model.
is a goal estimation function under the statistical model.
Example 2.6
We are given 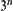 coins, one of which is known to be heavier or lighter than the rest. Using a two-pan scale, we divide the coins into three groups equally: A, B, C. First, group A is compared with B. A or B will contain the counterfeit coin in case the scale tips and C will contain the counterfeit one in case the scale balances. In terms of distribution function
coins, one of which is known to be heavier or lighter than the rest. Using a two-pan scale, we divide the coins into three groups equally: A, B, C. First, group A is compared with B. A or B will contain the counterfeit coin in case the scale tips and C will contain the counterfeit one in case the scale balances. In terms of distribution function 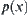 , we have:
, we have:
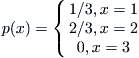
Here, 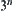 coins are assumed to be divided into three groups at random. Thus, the counterfeit coin falls in each group with same probability
coins are assumed to be divided into three groups at random. Thus, the counterfeit coin falls in each group with same probability 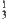 . We have:
. We have: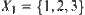 .
.
![]()
In other words, so long as increasing a certain amount of computation on 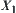 , the value of goal function
, the value of goal function 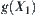 can always be reduced. Taking this into account, we have the following definition.
can always be reduced. Taking this into account, we have the following definition.
Definition 2.4
Assume that 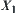 is a quotient space of X.
is a quotient space of X. 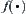 is a computational complexity function of X. Besides the amount
is a computational complexity function of X. Besides the amount 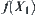 of computation on
of computation on 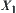 , an additional amount y of computation is added. Then, the goal distribution function is changed to
, an additional amount y of computation is added. Then, the goal distribution function is changed to 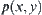 . Let
. Let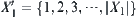 .
.
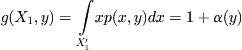
Certainly, the computational complexity above depends on the forms of 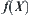 and
and 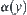 .
.
Now, we only discuss two specific kinds of 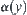 , i.e.,
, i.e., 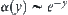 and
and 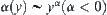 .
.
![]()
We know that when y increases, then 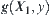 decreases. From Formula (2.4),
decreases. From Formula (2.4),  decreases as well. Certainly, the reduction of computational complexity is at the cost of additional computation y. But the point is how to choose an appropriate y and t such that the total computational complexity will be decreased. The following proposition gives a complete answer.
decreases as well. Certainly, the reduction of computational complexity is at the cost of additional computation y. But the point is how to choose an appropriate y and t such that the total computational complexity will be decreased. The following proposition gives a complete answer.
Proposition 2.5
Assume 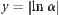 . If the number of granular levels is
. If the number of granular levels is 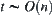 , the computational complexity is the minimal by using the multi-granular computing with t levels. And its asymptotic complexity is
, the computational complexity is the minimal by using the multi-granular computing with t levels. And its asymptotic complexity is 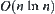 , where the number of elements in X is assumed to be
, where the number of elements in X is assumed to be 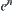 .
.
Proof:
Assume that the local partition approach is adopted and 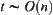 .
.
Let 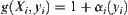 , where
, where 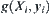 is the goal estimation function in the i-th granular level (abstraction level), when the additional computation is
is the goal estimation function in the i-th granular level (abstraction level), when the additional computation is 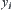 .
.
Proposition 2.4 shows that if 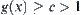 , by local partition method the computational complexity cannot be reduced. In order to reduce the complexity, it is demanded that
, by local partition method the computational complexity cannot be reduced. In order to reduce the complexity, it is demanded that 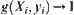 , i.e.,
, i.e., 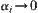 .
.
Now, let
![]() (2.7)
(2.7)
On the other hand, the total amount of additional computation is:
![]()
The total computational complexity is 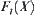 .
.
![]()
We'll show below that if t is not equal to 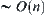 , the asymptotic complexity of
, the asymptotic complexity of 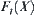 will be greater than or equal to
will be greater than or equal to 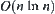 . There are three cases.
. There are three cases.
(1) If 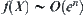 , letting
, letting 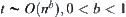 , then
, then 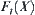 is divergent.
is divergent.
Assume that 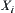 is a quotient space at the i-th granular level. Let
is a quotient space at the i-th granular level. Let 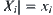 . Due to the local partition, we have
. Due to the local partition, we have 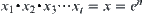 .
.
By letting each 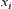 be d, obtain
be d, obtain 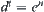 , i.e.,
, i.e., 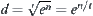 .
.
From 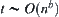 , we have
, we have 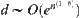 .
.
Again, from 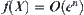 , we have
, we have 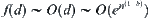 .
.
Substituting the above result into Formula (2.4), it follows that 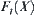 is divergent.
is divergent.
(2) If 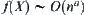 , when
, when 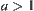 , letting
, letting 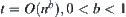 , the order of
, the order of 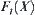 will not be less than
will not be less than 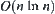 .
.
Similar to the inference in (1), we have 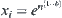 . By letting
. By letting 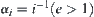 , we obtain
, we obtain 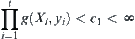 . Substituting the result into Formula (2.4), we obtain:
. Substituting the result into Formula (2.4), we obtain: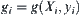
![]()
Thus,
![]()
On the other hand, the additional amount 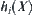 of computation is
of computation is
![]()
Finally,
![]() (2.8)
(2.8)
Letting the order of Ft(X) in Formula (2.8) be less than 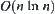 , it's known that the necessary and sufficient condition is:
, it's known that the necessary and sufficient condition is:
![]()
This is in contradiction with 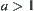 . Thus, the order of
. Thus, the order of 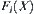 is not less than
is not less than 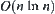 .
.
(3) If t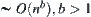 , the order of
, the order of 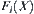 is
is 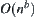 at least, or greater than
at least, or greater than 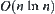 .
.
From Formula (2.4), it's known that 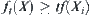 . Thus,
. Thus, 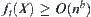 . Since
. Since 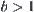 , the order of
, the order of 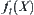 is greater than
is greater than 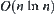 . Still more, the order of Ft(X) is greater than
. Still more, the order of Ft(X) is greater than 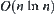 .
.
From the results of (1), (2) and (3), we conclude that the order of complexity is minimal by using the multi-granular computing with 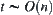 levels.
levels.
![]()
Proposition 2.6
Assume that 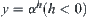 and
and 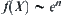 . If
. If 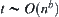 , then we have:
, then we have:
(i) when 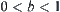 ,
, 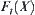 is divergent;
is divergent;
(ii) when 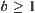 , if
, if 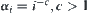 , then
, then 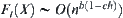 ;
;
(iii) when 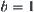 , if
, if 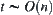 ,
,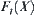 is minimal and its order is
is minimal and its order is 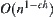 .
.
Proof:
When 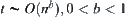 , from Proposition 2.5 (1), it's known that
, from Proposition 2.5 (1), it's known that 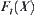 is divergent.
is divergent.
The additional amount 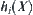 of the computation is
of the computation is
![]()
Thus,
![]()
Since
![]()
From the result above, it's known that the order of 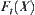 is minimal, when b=l, by using the multi-granular computing with
is minimal, when b=l, by using the multi-granular computing with 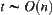 levels.
levels.
Proposition 2.7
Assume that 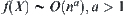 and
and 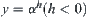 . Let
. Let 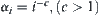 . When
. When 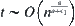 , where
, where 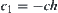 , the order of
, the order of 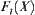 is minimal and equals
is minimal and equals 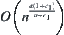 . It is less than the order of f(X).
. It is less than the order of f(X).
Proof:
If 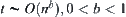 , from Proposition 2.6, we have
, from Proposition 2.6, we have 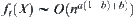 .
.
If the additional amount 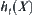 of computation satisfies
of computation satisfies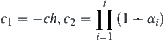 , finally, we have
, finally, we have
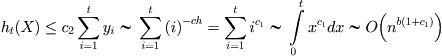
![]() (2.9)
(2.9)
In order to have the minimal order of 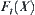
![]()
When  , the order of
, the order of 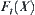 is minimal at
is minimal at 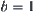 and equal to
and equal to 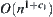 .
.
When 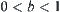 , letting
, letting 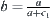 , the order of its corresponding
, the order of its corresponding 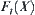 is minimal and equal to
is minimal and equal to 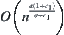 . Since
. Since 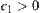 ,
, 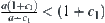 . So the order
. So the order 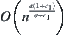 is less than
is less than 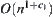 .
.
Finally, when 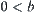 , letting
, letting 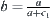 , the order of
, the order of 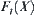 is minimal and equal to
is minimal and equal to 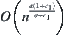 .
.
Proposition 2.8
If 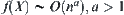
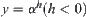 and
and 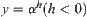 , by letting
, by letting 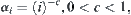 then
then 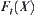 is divergent.
is divergent.
Proof:
From 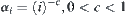 , we have
, we have
![]()
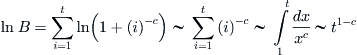
From 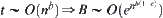 , we obtain B is divergent so that
, we obtain B is divergent so that 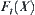 is divergent.
is divergent.
Proposition 2.9
If 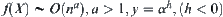 and
and 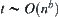 , then
, then
(1) when 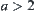 , by letting
, by letting 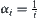 , the order of
, the order of 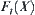 is less than that of
is less than that of 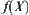 .
.
(2) when 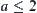 , by letting
, by letting 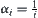 , the order of
, the order of 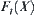 is not less than that of
is not less than that of 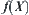 .
.
Proof:
Taking the logarithm on both sides of the above formula, we have
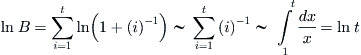
Thus, 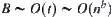
Substituting into Formula (2.4), we have
![]()
The order of the additional computation is 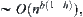 since c=1, hence
since c=1, hence
![]()
For the order of 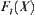 to reach the minimal,
to reach the minimal,
![]()
For the order of 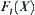 to be less than that of
to be less than that of 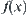 ,
,
![]()
Since 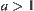 , have
, have 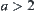 . When
. When 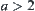 , the order of
, the order of 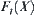 is less than that of
is less than that of 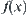 . When
. When 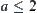 , the order of
, the order of 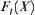 is not less than that of
is not less than that of 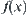 .
.
In summary, although the complexity estimation models we use are rather simple, the results of our analysis based on these models can completely answer the questions we raised at the beginning of this chapter. That is, in what conditions the multi-granular computing can reduce the computational complexity; under different situations, in what conditions the computational complexity can reach the minimal. These results provide a fundamental basis for multi-granular computing.
The results we have already had are summarized in Table 2.1, but only dealing with 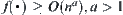 .
.
Applications
From the conclusions we made in Propositions 2.5–2.9, it is known that there indeed exist some proper multi-granular computing methods which can make the order of complexity Ft(X) less than that of the original one 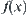 . To the end, the condition needed is that the corresponding
. To the end, the condition needed is that the corresponding 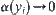 when the additional amount
when the additional amount 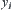 of computation at each granular level increases. Namely,
of computation at each granular level increases. Namely, 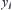 should grow at a negatively polynomial rate with
should grow at a negatively polynomial rate with 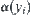 , i.e.,
, i.e., 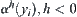 . The problem is if there exists such a relation between
. The problem is if there exists such a relation between 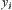 and
and 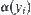 objectively. We next discuss the problem.
objectively. We next discuss the problem.
Table 2.1
The order of Computational Complexity at Different Cases
| Compared to f(⋅) | ||||||
| O(n) | < | |||||
| b≥1 | ||||||
| b=1 | ||||||
| 0<b<1 | < | |||||
| a > 2 | y=αh h<0 | < | ||||
| 1 ≤ a ≤ 2 | ≥ | |||||

Where b∗ is the optimal value of b.
Assume that 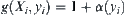 is the goal estimation function under the nondeterministic model with additional computation
is the goal estimation function under the nondeterministic model with additional computation 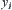 . In order for
. In order for 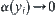 , if
, if 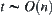 , then
, then 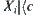 (constant) and the corresponding distribution function
(constant) and the corresponding distribution function 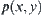 at
at 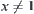 has to be arbitrarily small. This is equivalent to the goal falling into a certain element with probability one when the additional computation
has to be arbitrarily small. This is equivalent to the goal falling into a certain element with probability one when the additional computation 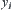 gradually increases. In statistical inference, it is known that so long as the sample size (or the stopping variable in the Wald sequential probabilistic ratio test) gradually increases the goal can always be detected within a certain element with probability one. Therefore, if regarding the sample size as the additional amount of computation, there exist several statistical inference methods which have the relation
gradually increases. In statistical inference, it is known that so long as the sample size (or the stopping variable in the Wald sequential probabilistic ratio test) gradually increases the goal can always be detected within a certain element with probability one. Therefore, if regarding the sample size as the additional amount of computation, there exist several statistical inference methods which have the relation 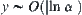 , where the meaning of
, where the meaning of  is the same as that of the
is the same as that of the  in the formula
in the formula 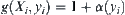 . Then, from Proposition 2.5, it shows that if a proper statistical inference method is applied to multi-granular computing methods, the order of complexity
. Then, from Proposition 2.5, it shows that if a proper statistical inference method is applied to multi-granular computing methods, the order of complexity 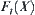 can reach
can reach 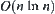 regardless of the form of the original complexity f(X).
regardless of the form of the original complexity f(X).
2.2.4. Successive Operation in Multi-Granular Computing
From the probabilistic model, it shows that some elements in a certain granular level which contain the goal can only be found with certain probability. It implies that the elements we have already found might not contain any goal. Thus, the mistakes should be corrected as soon as they are discovered. By tracing back, we can go back to some coarse granular level and begin a new round of computation. In our terminology, it is called successive operation. In Chapter 6, we'll show that under certain conditions, by successive operation the goal can be found with probability one but the order of complexity does not increase at all.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
