For a problem space
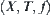
, given the knowledge of its two abstraction levels
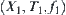
and
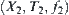
, we intend to have an overall understanding about
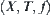
.
Assume that the overall understanding of
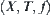
is represented by
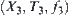
. We are now going to discuss how to construct
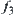
from
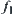
and
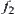
such that it satisfies the synthetic principles.
3.6.1. The Synthetic Principle of Attribute Functions
Given a problem space
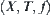
and its quotient spaces
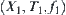
and
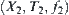
. Let

, be nature projections.
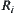
is an equivalence relation with respect to quotient space
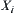
.
Fixing projection
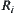
,
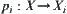
is uniquely defined. When
T is a topology, including a semi-order, fixing
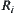
,
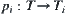
is also uniquely defined.
Once the approach of constructing the global attributes of set
A from its local information is determined, projection
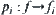
is uniquely defined too.
Conversely, two spaces
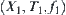
and
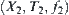
are given. Let

. Their synthetic space
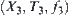
must satisfy the following three conditions at least
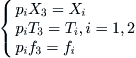 (3.1)
(3.1)
In general, the solution satisfying constraints
(3.1) is not unique. In order to have a unique solution, additional optimization criteria have to be provided generally. In Section
3.3, the optimization goal of the synthetic space
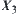
is represented by ‘the least upper bound’ criterion. In Section
3.4, the optimization goal of the synthetic topology is indicated by ‘the coarsest’ criterion.
We now present the synthetic principle of attribute functions as follows.
Given
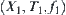
and
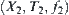
, find the synthetic space
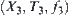
satisfying the following conditions.
(1) 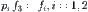 (3.2)
(3.2)
where
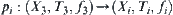
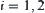
, is a natural projection.
(2) Assume that
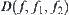
is a given optimization criterion. Then
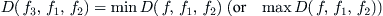 (3.3)
(3.3)
where, the min (max) operation is carried on all attribute functions in
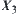
which satisfy Formula
(3.2).
We next show the rationality of the above synthetic principles.
The condition (1), i.e.,
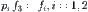
, is necessary. That is, the projections of
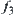
on
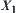
and
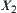
must be identical with the given
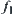
and
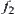
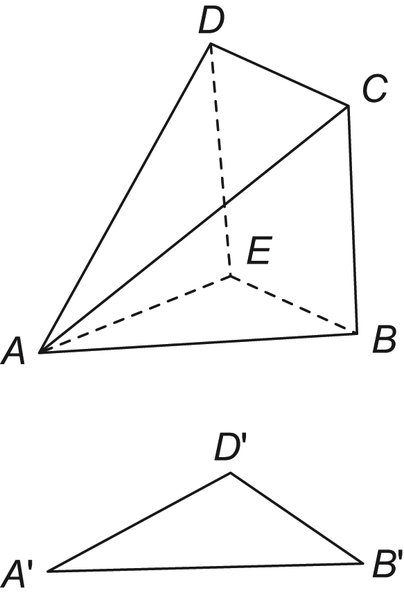
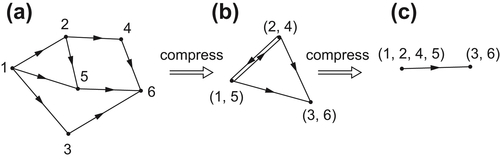
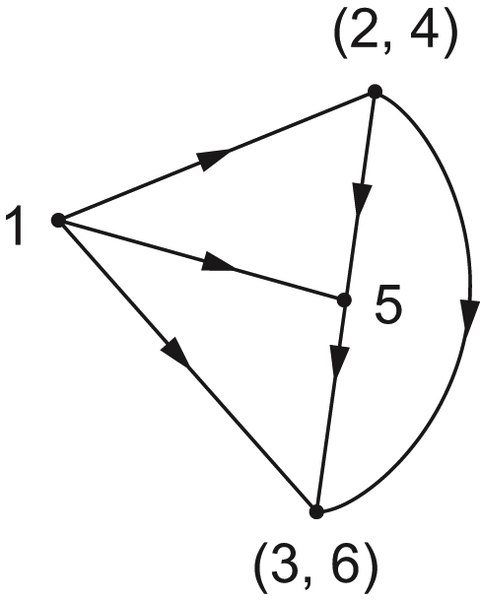
, respectively. As shown in
Example 3.4, the corresponding projections of the object
S synthesized from the given front and top views have to be identical to the given triangles
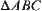
and
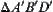
at least, respectively, as shown in
Fig. 3.1.
In fact, the solution satisfying constraint
(3.2) is not unique. This is not necessarily a bad thing. For example, when designing a mechanical part, we have to consider several requirements and each requirement can be regarded as a kind of constraint on its abstraction level. Generally, the design result satisfying these requirements is not unique. This means there is plenty of room for designers’ imaginations. The design works will benefit from the variety of the results. But this is an obstacle to a computer while it is not intelligent enough. So in computer problem solving, some sort of optimization criteria are needed.
Condition (2) above is one such optimization criterion. As long as it is given, the computer will be able to find the optimal solution. For example, we design a container in
order to satisfy the requirements shown in
Fig. 3.1. That is, its front and top views are triangles
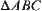
and
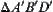
, respectively. For human designers, under such requirements, an infinite variety of designs can be envisioned. But, in order to have a solution by a computer, a specific criterion must be provided. For example, if taking the maximal volume of the container as a criterion then a cone ABCDE shown in
Fig. 3.1 will be turned out.
Generally, the optimal synthetic criteria are domain-dependent and hard for computers to implement. In reality, we can only have some so-called satisfactory solutions. This is one of the main ideas in artificial intelligence.
In fact, in the real world, the situation is more complicated. For example, the information that we have in some abstraction level is not precise. Therefore, we have to handle the imprecise or incomplete information.
We are given spaces
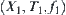
and
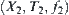
. Let
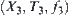
be a synthetic space.
Let
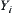
be a space consisting of all attribute functions on
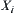
. Assume that there exists a metric
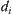
in each
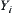
such that
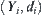
,
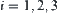
,
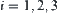
, is a metric space.
Now, if the observation in level
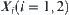
is not precise, so Formula
(3.2) may not hold accurately. Similar to the method of least-squares, we establish the following relation.
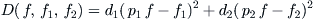 (3.4)
(3.4)
where,
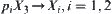
, is a natural projection. And
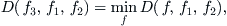 (3.5)
(3.5)
where, the operation min is carried on all functions on
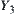
.
If function
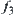
satisfying Formula
(3.5) is still not unique, an additional criterion is needed, for example, an additional function
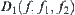
. By letting
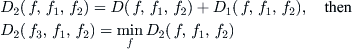 (3.6)
(3.6)
where, the operation min is carried on all functions on
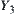
as well.
Attribute function
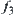
that obtained from
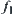
and
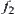
by Formulas
(3.4) and
(3.5), or by Formula
(3.6), is a synthetic one.
As mentioned above, the optimization synthetic criteria are generally domain-dependent, and there is a great variety of methods for extracting global information from local ones, i.e., a variety of
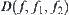
functions. Therefore, it is hard to have a universal optimization criterion.
3.6.2. Examples
In this section, we will explain the computed tomography, CT for short, by our synthetic model in order to have a better understanding of the model.
Example 3.11
As shown in
Fig. 3.6,
T is a biological tissue under study, by placing an X-ray and photosensitive film DE alongside the tissue so that it lies perpendicular to the incident rays. When the X-ray traverses from left to right along the x-axis, an image on film DE of X-ray attenuation during this traverse is obtained. The image of the tissue's structure can be reconstructed by using a computer to analyze a set of these recorded images. This is the basic principle of computed tomography (
Kak and Slaney, 2001).
When a beam of X-rays penetrates any structure shown in
Fig. 3.6, attenuation occurs, the degree of the attenuation is related to: (a) the atomic number of the element of which the structure is composed, or the effective atomic number of a complex structure and (b) the concentration of the substances forming that structure. Thus, the density of electrons, or effective electron density, determines the degree to which a given beam of X-rays will be attenuated. Therefore, from the attenuation of the X-ray the structure of a tissue being tested can be known.
In
Fig. 3.6, we now assume that
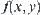
is the attenuation coefficient of that tissue at (
x,
y) in one of its cross-sections. When X-ray passes through the given structure, the density of the beam emerging from the other side of the structure will depend on
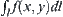
. The one-dimensional image recorded in film DE is
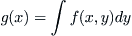 (3.7)
(3.7)
when X-ray traverses along the x-axis.
Figure 3.6 The Principle of CT In terms of hierarchical model, the attenuation coefficient
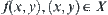
can be regarded as an attribute function of a problem space
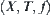
, where
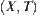
is a part of two-dimensional Euclidean space, e.g., a cross-section of a tissue as shown in
Fig. 3.6.
From Formula
(3.7), we can see that
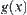
is a projection of
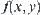
on
X. It forms a new space
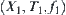
, where
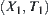
is a quotient space of
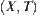
by considering each line perpendicular to the x-axis as a point, i.e., an equivalence class. Thus,
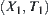
is a line segment DE on the x-axis. The relation between attribute functions
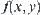
and
g(
x) is the following.
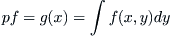
where
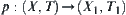
For each line
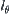
intersecting the x-axis with angle

, we have a projection
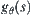
.
For all
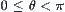
, we have a set
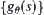
of projections. Then, we obtain a set of quotient spaces denoted by
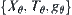
,
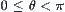
.
The point is how to find
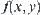
from a set
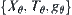
,
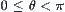
of quotient spaces. This is the same problem that CT intends to solve.
From the hierarchical model viewpoint, it is to find a synthetic space from a given set
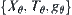
of quotient spaces. That is, given
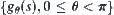
, we find a
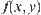
such that it satisfies:
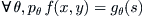 (3.8)
(3.8)
where
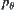
:
X →
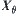
is a projection,
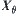
is a domain of
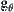
(s).
Letting
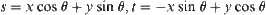
, we have
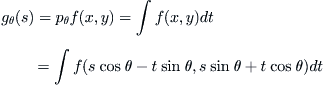
In mathematics, it can be proved that a set of
equations (3.8) has a unique solution. So there is no need of additional criteria in the synthetic model. The synthetic attribute function can be obtained by solving Formula
(3.8) directly.
From the theorems of Fourier transform, we have the following theorem.
Theorem 3.2
The Fourier transform of the one-dimensional projection of a two-dimensional function is identical with the distribution on the central section of the Fourier transform of that function.
The theorem can be stated by the following mathematical formulas.
The Fourier transform of function
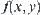
is as follows.
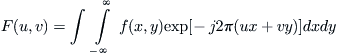
The projection of
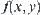
on
X is
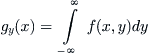
The Fourier transform of
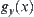
is
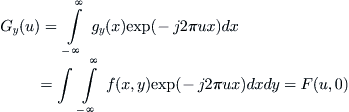
Let
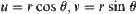
, we have
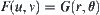
.
By Fourier inverse transform of
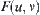
, we have
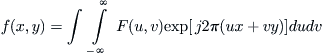
Therefore, from a given set
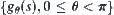
, we have a Fourier transform
. Meanwhile, from the Fourier inverse transform of
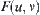
, we finally have
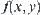
. In CT,
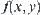
corresponds to the image of the biological tissue being radiographed. Thus, the computed tomography is a special case of our synthetic problem, while there is no need for the optimal criteria.
Example 3.12
In reality, the reconstruction of
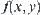
by the method indicated in
Example 3.11 may not be feasible, since an infinite number of projections are needed. For this reason,
Kashyap and Mittal (1975) presented a minimization approach to algebraic equations. We first briefly explain their approach in the way of our hierarchical model.
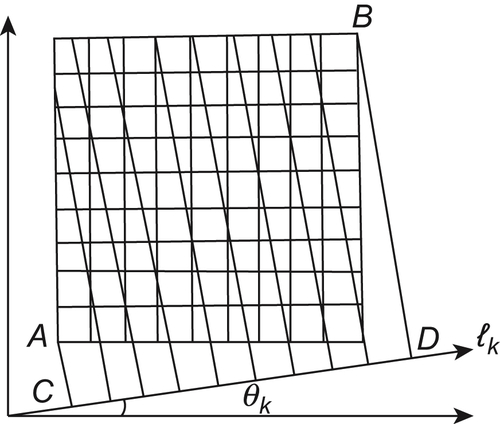
Assume that the domain
X of
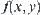
is a square. Then, each edge of the square is equally divided into
n intervals. We have a mesh consisting of
n×n blocks. Regarding each block
as a point, the value of
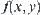
at its center is considered as the value of
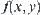
in that block.
Regarding each block as an equivalence class, the mesh is a quotient space denoted by
X. Taking the value of
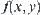
at the central point of each block as the value of
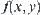
in the block, which is called the inclusion principle, one of the basic approaches for constructing global information as mentioned in
Chapter 2.
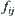
indicates the value of
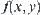
at the central point of the
ij-th block (the block at the
i-th row and the
j-th column). Arranging
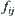
according to the dictionary order of subscript (
i,j), we have a
n2-dimensional vector
f as follows.
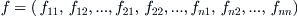
Then,
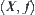
is a problem space after the discretization.
We draw a radial
lk that intersects the horizontal line at angle
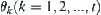
. From vertexes
A and
B, we draw two lines perpendicular to
lk at points
C and
D, respectively. Then, line
CD is divided into
n intervals equally. From each end point of the intervals we draw a line perpendicular to
lk and have
n regions of square
X (
Fig. 3.7). From left to right, the regions are denoted by
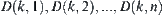
, respectively.
Let
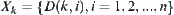
.
Obviously,
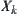
is a quotient space of
X.
Define
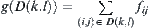
.
That is,
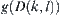
is the sum of
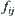
over the range of region
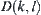
, or denoted by
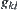
for short.
Define
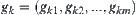
.
Figure 3.7 The Discrete Method of CT Therefore,
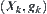
is a quotient space of
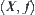
.
Given
t projections
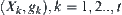
, we find their synthetic space
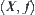
. This is just the problem that CT intends to solve.
Changing the subscript of the vector
f, we have
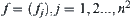
. Let
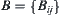
be a
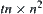
matrix. Then
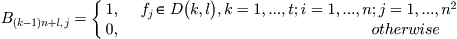
From the synthetic principles,
f must satisfy the following formula.
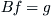 (3.9)
(3.9)
where,
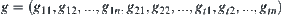
.
From linear algebra, we know that if
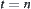
, then
Equation (3.9) has a unique solution. The
f obtained from
Equation (3.9) is the synthetic attribute function, or the image of biological tissue being examined after discretization.
If
t>
n generally, there is no solution to
Equation (3.9). Similar to the method of least-squares, we construct a metric function
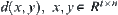
in
t ×
n dimensional Euclidean space. Let
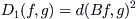 (3.10)
(3.10)
The synthetic attribute function
f is the one that makes the right hand side of Formula
(3.10) minimum.
If
t<
n,
Equation (3.9) has an infinite solution. It is necessary to introduce an optimal criterion such as
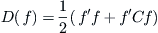 (3.11)
(3.11)
where
C is a positive semi-definite matrix related to local smoothness,
f′ is a
n2-dimensional column vector. The synthetic attribute function
f is the one that satisfies constraint
(3.9) and makes the right hand side of Formula
(3.11) minimum.
From Lagrange multiplier procedure, we have
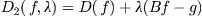 (3.12)
(3.12)
Finding the minimum of Formula
(3.12), we have
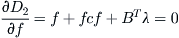 (3.13)
(3.13)
Where,
BT is the transposed matrix of B. Formula
(3.12) is simplified to
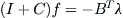
Since (
I+
C) is not singularity, we have
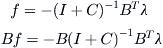
That is,
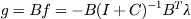
Since when
t<
n,
B is not singularity, using pseudo-inverse we have
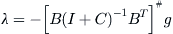
where, ‘#’ denotes the pseudo-inverse operation,
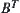
is the transpose of matrix
B.Finally, we have
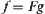
, where
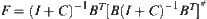
.
f is the synthetic attribute function, i.e., the function corresponding to the sectional images after discretization in computed tomography.
Next, we give a mathematical example which can be regarded as an application of the synthetic model.
Example 3.13
X is a linear normed space. Given a
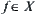
, since itself may be rather complicated, we project
f on a simpler space, for example, a real number axis. Assume
A X∗
X∗, where
X∗ is a conjugate space of
X, i.e.,
X is a space consisting of all linear bounded functionals on
X. For
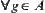
, functional
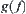
is known. The problem is how to deduce
f from
g(
f). By the synthetic viewpoint, it means that constructing
f from the known
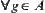
,
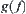
.
Let
L(
A) be a linear sub-space on
X∗ containing
A. Fixed
f,
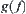
varying within
L(
A), then
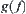
is a linear functional on
L(
A), and is denoted by
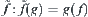
. Assuming
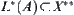
,
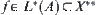
.
Assume further that
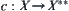
is a canonical mapping which embeds
X within
X∗∗ and there exists c
−1. By letting
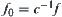
,
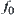
is just the synthesis of
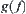
,
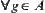
.
Assume that X is a Euclidean space.
A set of equations is given below.
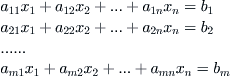 (3.14)
(3.14)
We can write Formula
(3.14) in vectorial form
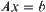
. Each row can be represented by
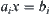
,
i=1,2…
m.
Regarding vector
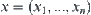
as a point in space
En and
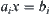
as a value of linear functional
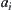
at point
x. Letting
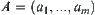
,
L(
A) is a sub-space supported by
m vectors.
If
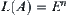
, Formula
(3.14) has a unique solution, i.e.,
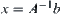
. If
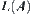
is a proper subset of
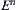
, Formula
(3.14) has an infinite number of solutions. Then, we introduce an optimal criterion
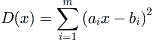
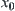
is the optimal solution with a minimal
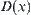
. From the geometrical point of view,
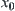
on
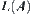
has a shortest distance from
x, and is regarded as the real value of
x.
The example shows that solving a set of equations, or a constraint satisfaction problem, can be regarded as information synthesis.
In
Chapter 4, uncertain reasoning will be studied by the synthetic model.
3.6.3. Conclusions
In this section, we present a synthetic model under the quotient space theory.
Spaces
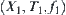
and
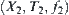
are given.
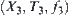
is their synthetic space. We have
(1) The synthesis of domains: X3 is the least upper space of X1 and X2
(2) The synthesis of topological structures: T3 is the least upper topology of T1 and T2.
(3) The synthesis of attribute functions:
f3 satisfies the following condition
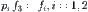
, where
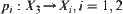
, is a natural projection. If
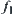
and
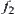
have error, then the above formula will be replaced by the following formula.
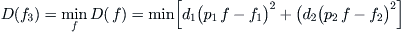
Where
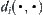
is a metric function on
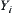
,
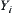
is all attribute functions on
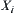
, and the min operation is carried out on all attribute functions
f on
X3.
If the solution is not unique, a proper optimal criterion must be added in order to have an optimal solution.
The synthetic model can be applied to constraint satisfaction problems, reasoning processes, etc.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
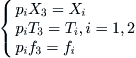 (3.1)
(3.1)![]() (3.2)
(3.2)![]() (3.3)
(3.3)![]() (3.4)
(3.4)![]() (3.5)
(3.5)![]() (3.6)
(3.6)![]() (3.7)
(3.7)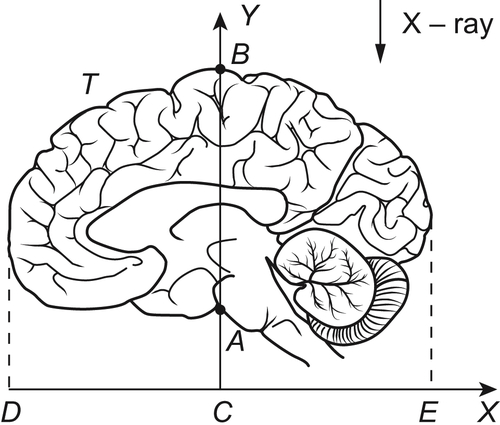
![]()
![]() (3.8)
(3.8)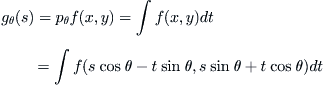
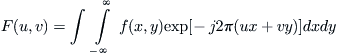
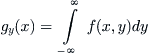
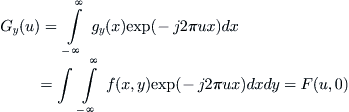
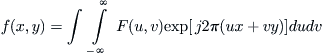
![]()
![]()
![]() (3.9)
(3.9)![]() (3.10)
(3.10)![]() (3.11)
(3.11)![]() (3.12)
(3.12)![]() (3.13)
(3.13)![]()
![]()
![]()
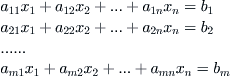 (3.14)
(3.14)![]()
![]()
