7.3. Fractal Geometry and Quotient Space Analysis
7.3.1. Introduction
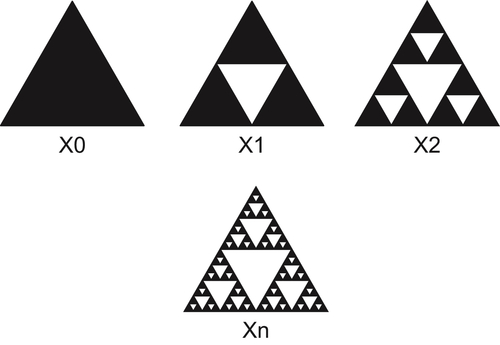
A famous Sierpinski carpet is shown in Fig. 7.2. It’s a typical fractal graph. From the quotient space view point, it’s a chain of quotient spaces, where 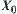 has one element,
has one element, 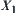 has four and
has four and 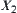 has 13 elements. Therefore, the concepts of quotient space and fractal geometry have a close relation. We will discuss them using the quotient space approximation principle in the following sections.
has 13 elements. Therefore, the concepts of quotient space and fractal geometry have a close relation. We will discuss them using the quotient space approximation principle in the following sections.
7.3.2. Iterated Function Systems
In order to investigate fractal graphs from quotient space theory, the concept of quotient fractals is established first. Then, the quotient fractals are used to approximate fractal graphs. Its procedure is the following. An equivalence relation is defined through a mapping. A corresponding chain of hierarchical quotient spaces is built by the equivalence relation. Then, quotient mappings are set up on the quotient spaces. Finally, quotient fractals are obtained from the quotient mappings.
Definition 7.19
A set 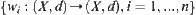 of compressed mappings on a compact metric space
of compressed mappings on a compact metric space 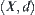 is given, where compression factor
is given, where compression factor 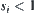 . Let
. Let 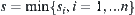 . It is called an iterated function system on
. It is called an iterated function system on  , simply denoted by
, simply denoted by 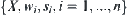 .
.
Definition 7.20
Assume that 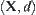 is a complete metric space.
is a complete metric space. 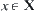 ,
, 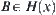 , where H(x) is a power set of
, where H(x) is a power set of  . Define
. Define 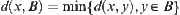 .
.  is called a distance from point
is called a distance from point  to set
to set  .
.
Definition 7.21
Assume that 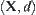 is a complete metric space. Sets
is a complete metric space. Sets 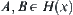 , define
, define 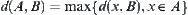 .
. 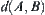 is called a distance from set
is called a distance from set 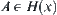 to set
to set 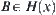 .
.
Definition 7.22
The main theorem in iterated function systems is the following.
Theorem 7.4 (Attractor Theorem)
Assume that 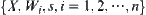 is an iterated function system on X. W is a fractal mapping on X. Then,
is an iterated function system on X. W is a fractal mapping on X. Then, 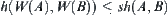 holds on (H(x),h(d)). Namely, there exists a unique fixed point P on H(x), i.e.,
holds on (H(x),h(d)). Namely, there exists a unique fixed point P on H(x), i.e.,
![]()
P is a corresponding fractal graph on iterated function system IFS=W.
7.3.3. Quotient Fractals
A mapping is used to define an equivalence relation as follows.
Definition 7.23
An iterated function system 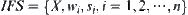 on
on  is given. Construct
is given. Construct 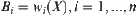 and
and 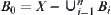 . Letting
. Letting 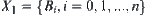 , then
, then 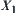 is a quotient space of
is a quotient space of  .
.
Now, 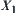 is partitioned as follows, i.e.,
is partitioned as follows, i.e.,  is partitioned as
is partitioned as 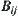 . Let
. Let
![]()
We obtain
![]() (7.16)
(7.16)
Set 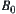 remains unchanged.
remains unchanged.
Then, we have a partition of  denoted by
denoted by 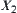 . From Formula (7.16), it’s known that
. From Formula (7.16), it’s known that 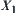 is a quotient space of
is a quotient space of 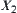 .
.
By induction, assume that 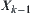 is a known quotient space. For its elements, the partition procedure is the following. Let
is a known quotient space. For its elements, the partition procedure is the following. Let
![]()
We obtain
![]()
Obviously, 
 compose a chain of hierarchical quotient spaces. For simplicity, the element
compose a chain of hierarchical quotient spaces. For simplicity, the element 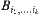 of
of 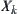 is denoted by its subscript
is denoted by its subscript 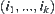 in the following discussion.
in the following discussion.
Definition 7.24
Define a mapping 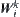 on
on 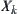 as
as 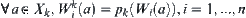 , where
, where 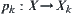 is a nature projection and
is a nature projection and 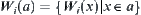 .
.
Definition 7.25
Define 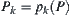 on
on 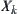 , where
, where 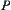 is an invariant subset on
is an invariant subset on  corresponding to mapping W, i.e., a fractal graph.
corresponding to mapping W, i.e., a fractal graph.
Definition 7.26
Theorem 7.4
If an iterated function system IFS on  is given, then it corresponds to a chain of hierarchical quotient sets on
is given, then it corresponds to a chain of hierarchical quotient sets on  .
.
Proof
Assume that mapping 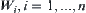 . Let
. Let 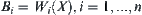 and
and 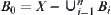 .
.
(1) Assume that 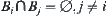 . Then,
. Then, 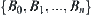 compose a partition of X. Its corresponding quotient space is denoted by
compose a partition of X. Its corresponding quotient space is denoted by 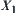 . Again, let
. Again, let  and
and 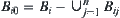 . Then,
. Then, 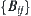 compose a partition of
compose a partition of  denoted by
denoted by 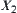 . Obviously,
. Obviously, 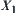 is a quotient space of
is a quotient space of 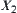 .
.
By induction, define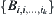 compose a partition of X denoted by
compose a partition of X denoted by 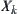 . It’s easy to show that
. It’s easy to show that 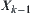 is a quotient space of
is a quotient space of 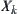 .
.
![]()
![]()
Therefore, 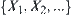 is a chain of quotient sets of X or a chain of quotient spaces corresponding to an iterated function system.
is a chain of quotient sets of X or a chain of quotient spaces corresponding to an iterated function system.
(2) When some  and
and  are overlapping, i.e.,
are overlapping, i.e., 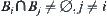 . An abstract space
. An abstract space 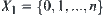 can be constructed, where element i corresponds to set
can be constructed, where element i corresponds to set  . Define an abstract space
. Define an abstract space  , where element
, where element 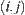 corresponds to set
corresponds to set 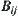 , i.e.,
, i.e.,  .
.
Generally, define 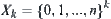 , where element
, where element 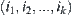 corresponds to
corresponds to 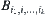 ,
, 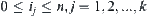 . Let
. Let 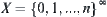 . The point on
. The point on  is an infinite sequence composed by 0,1,…,n, i.e.,
is an infinite sequence composed by 0,1,…,n, i.e., 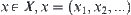 .
.
Similarly, we may have a chain  of quotient sets.
of quotient sets.
We have a profound relation between quotient fractals and fractal graphs as follows.
Theorem 7.5 (Quotient Fractal Approximation Theorem)
We have the following properties.
Property 1
![]()
Property 3
Property 4
![]()
7.3.4. Conclusions
Property 3 in Section 7.3.3 is the quotient fractal approximation theorem of fractal graphs. It means that in fractal geometry we can still use a set of simple quotient spaces to approximate the original space so that the computational complexity is reduced. This is just the basic principle of quotient space approximation method and the multi-granular computing as well.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
