Addenda A
Some Concepts and Properties of Point Set Topology
A.1. Relation and Mapping
A.1.1. Relation
Definition 1.1.1
Definition 1.1.2
Assume that R is a relation from X to Y. If 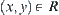 , then x and y are
, then x and y are 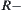 relevant, denoted by
relevant, denoted by 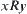 .
.
Set 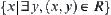 is called the domain of R, denoted by
is called the domain of R, denoted by  .
.
Set 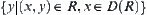 is called the range of R, denoted by
is called the range of R, denoted by 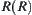 .
.
For 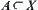 , letting
, letting 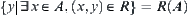 ,
, 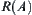 is called a set of images (or image) of A.
is called a set of images (or image) of A.
For  , letting
, letting 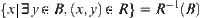 ,
, 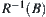 is called the preimage of B.
is called the preimage of B.
Definition 1.1.3
For 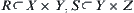 , letting
, letting 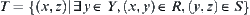 , T is called the composition of R and S, denoted by
, T is called the composition of R and S, denoted by  .
.
For 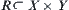 , letting
, letting 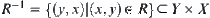 ,
, 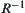 is called the inverse of R.
is called the inverse of R.
A.1.2. Equivalence Relation
Definition 1.2.1
Assume that R is a relation from X to X (or a relation on X) and satisfies
(1) 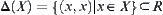 (Reflexivity)
(Reflexivity)
(2) 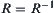 (Symmetry)
(Symmetry)
(3)  (Transitivity)
(Transitivity)
R is called an equivalence relation on X.
Assume that R is an equivalence relation on X. For 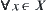 , letting
, letting 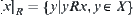 ,
, 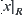 is an
is an 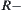 equivalent set of x.
equivalent set of x.
Definition 1.2.2
For 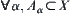 , if
, if 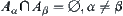 and
and 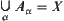 , then
, then 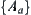 is a partition of x.
is a partition of x.
Proposition 1.2.1
R is an equivalence relation on X. Then, 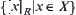 is a partition of X.
is a partition of X.
A.1.3. Mapping and One–One Mapping
Definition 1.3.1
F is a relation from X to Y. For 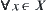 , if there exists a unique
, if there exists a unique 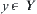 such that
such that  , then F is called a mapping from X to Y, denoted by
, then F is called a mapping from X to Y, denoted by 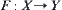 .
.
If 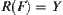 , F is called surjective, where
, F is called surjective, where  is the range of F.
is the range of F.
For 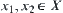 , if
, if 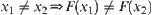 , F is called 1-1 mapping.
, F is called 1-1 mapping.
Proposition 1.3.1
f : is a mapping. For
is a mapping. For 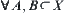 , we have
, we have
![]()
![]()
![]()
If 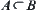 , then
, then  .
.
For 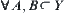 , we have
, we have
![]()
![]()
![]()
If 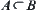 , then
, then 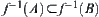 .
.
If f is surjective, then  ,
, 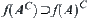 .
.
If f is a 1-1 mapping, then 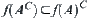 .
.
Where,  is the complement of A.
is the complement of A. 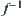 is the inverse of f.
is the inverse of f.
If f is surjective and 1-1 mapping, then 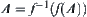 and
and 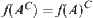 .
.
Definition 1.3.2
Assume that X is a Cartesian product of 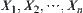 . Let
. Let 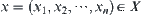 . Define
. Define  .
. 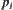 is the projection of X on
is the projection of X on 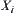 , or a set of the i-th coordinates.
, or a set of the i-th coordinates.
A.1.4. Finite Set, Countable Set and Uncountable Set
Definition 1.4.1
A and B are two sets. If there exists a 1-1 surjective mapping from A to B, A and B are called equinumerous.
Any set that is not equinumerous to its proper subsets is a finite set.
A set that is equinumerous to the set N of all natural numbers is a countable set.
An infinite set that is not equinumerous to the set N of all natural numbers is an uncountable set.
Theorem 1.4.1 (Bernstein)
If A and the subset of B are equinumerous, and B and the subset of A are also equinumerous, A and B are equinumerous.
A.2. Topology Space
A.2.1. Metric Space
X is a non-empty set.  is a mapping, where R is a real set.
is a mapping, where R is a real set. 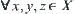 , d satisfies:
, d satisfies:
(2) 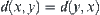
(3) 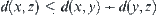
Then, d is a distance function on X and 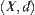 is a metric space.
is a metric space.
Definition 2.1.2
Proposition 2.1.1
(1)  , there is one neighborhood at least.
, there is one neighborhood at least.  , have
, have 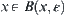 .
.
(2) 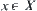 , for any two spherical neighborhoods
, for any two spherical neighborhoods  and
and 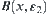 , there exists
, there exists 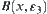 such that
such that  .
.
(3) If 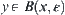 , then there exists
, then there exists 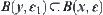 .
.
A.2.2. Topological Space
Definition 2.2.1
X is a non-empty set. 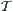 is a family of subsets of X. If
is a family of subsets of X. If 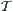 satisfies the following conditions
satisfies the following conditions
(1) 
(2) 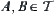 ,
, 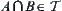
(3) 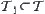 ,
, 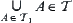
then Definition 2.2.2
For 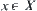 , the set of all neighborhoods of
, the set of all neighborhoods of  is called a system of neighborhoods of x, denoted by
is called a system of neighborhoods of x, denoted by 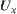 .
.
A.2.3. Induced Set, Close Set and Closure
Definition 2.3.1
For 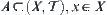 , if
, if 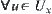 ,
, 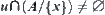 , then x is called an accumulation (limit) point of A.
, then x is called an accumulation (limit) point of A.
Set  of all accumulation points of A is called an induced set of A.
of all accumulation points of A is called an induced set of A.
Proposition 2.3.1
For 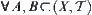 , we have
, we have
(1) 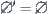
(2) 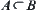
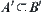
(3) 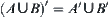
(4) 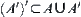
Definition 2.3.2
For  , if all accumulation points of A belong to A, then A is a close set.
, if all accumulation points of A belong to A, then A is a close set.
Proposition 2.3.2
A is close 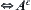 is open.
is open.
Proposition 2.3.3
Assume that 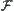 is a family of all close sets on
is a family of all close sets on 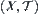 . We have
. We have
(1) 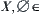
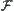
(2) If 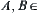
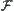 , then
, then 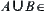
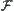 .
.
(3) If 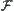 1
1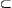
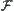 , then
, then 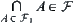 .
.
Definition 2.3.3
For  , letting
, letting 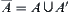 ,
, 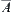 is called a closure of A.
is called a closure of A.
Definition 2.3.4
For 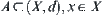 , define
, define  .
.
Proposition 2.3.5
For 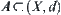 , we have
, we have
(1) 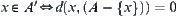
(2) 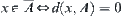
A.2.4. Interior and Boundary
Definition 2.4.1
For  , letting
, letting  ,
, 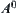 is called the interior (core) of A.
is called the interior (core) of A.
Proposition 2.4.1
For  , we have
, we have
(1) A is open 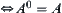
(2) 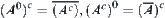
(3) 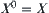
(4) 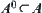
(5) 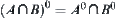
(6) 
Definition 2.4.2
For 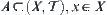 , if
, if 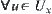 ,
, 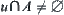 and
and 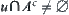 , x is called a boundary point of A. The set of all boundary points of A is called boundary of A, denoted by
, x is called a boundary point of A. The set of all boundary points of A is called boundary of A, denoted by 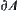 .
.
A.2.5. Topological Base and Subbase
Definition 2.5.1
Proposition 2.5.1
Proposition 2.5.2
Proposition 2.5.3
(1) 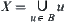
(2) If 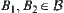 , for
, for  , there exists
, there exists  such that
such that  .
.
Then, let 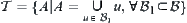 be a topology of X and
be a topology of X and 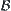 be a base of
be a base of 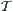 .
.
Definition 2.5.2
A.2.6. Continuous Mapping and Homeomorphism
Definition 2.6.1
If 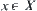 ,
,  and
and 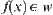 , have
, have 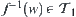 , then f is continuous at x.
, then f is continuous at x.
Proposition 2.6.1
For 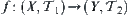 , the following statements are equivalent.
, the following statements are equivalent.
(1) f is a continuous mapping
(2) If 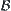 is a base of Y, then
is a base of Y, then 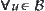 ,
, 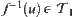 .
.
(4)  is a subbase of Y;
is a subbase of Y; 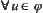 , have
, have 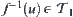 .
.
(5)  , have
, have 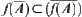 .
.
(6) 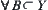 , have
, have 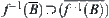 .
.
Proposition 2.6.2
For  , the following statements are equivalent.
, the following statements are equivalent.
(1) f is continuous at x.
(2) For all neighborhoods 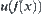 of
of  , there exists
, there exists 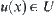 such that
such that 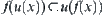 .
.
Proposition 2.6.3
If 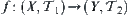 and
and 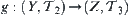 are continuous, then
are continuous, then 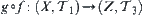 is continuous.
is continuous.
Definition 2.6.3
A.2.7. Product Space and Quotient Space
Definition 2.7.1
Similarly, we may define the concept of the largest (finest) topology.
Proposition 2.7.1
Assume that 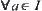 ,
, 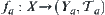 . There exists the smallest (coarsest) topology among topologies on X that make each
. There exists the smallest (coarsest) topology among topologies on X that make each 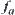 continuous.
continuous.
Proposition 2.7.2
Assume that 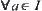 ,
, 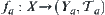 . There exists the largest (finest) topology among topologies on X that make each
. There exists the largest (finest) topology among topologies on X that make each 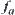 continuous.
continuous.
Corollary 2.7.2
Assume that 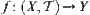 . There exists the largest (finest) topology among topologies on
. There exists the largest (finest) topology among topologies on 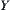 that make
that make 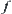 continuous. The topology is called the quotient topology with respect to
continuous. The topology is called the quotient topology with respect to 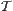 and
and 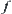 .
.
Definition 2.7.2
For 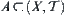 , letting
, letting 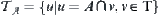 ,
, 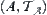 is called the subspace of
is called the subspace of  .
.
Definition 2.7.3
Assume that  , where
, where 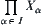 indicates the product set.
indicates the product set. 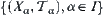 is a family of topologic spaces. Let
is a family of topologic spaces. Let 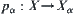 be a projection.
be a projection. 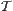 is the smallest topology among topologies on
is the smallest topology among topologies on 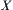 that make
that make  continuous.
continuous.  is called the product topologic space of
is called the product topologic space of  , denoted by
, denoted by 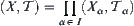 .
.
Proposition 2.7.3
Assume that  is a product topologic space of
is a product topologic space of 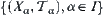 . Letting
. Letting 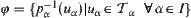 ,
,  is a subbase of
is a subbase of 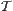 .
.
Proposition 2.7.4
Assume that  is a product topologic space of
is a product topologic space of 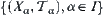 .
. 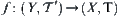 is continuous
is continuous 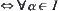 ,
, 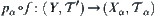 is continuous.
is continuous.
Proposition 2.7.5
Assume that  is a product topologic space of
is a product topologic space of 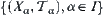 . Then, series
. Then, series 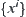 on X converges to
on X converges to 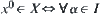 , series
, series 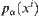 on
on 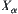 converges to
converges to  .
.
Where, the definition of convergence is that for 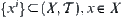 , if
, if 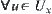 , there exists
, there exists 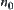 such that when
such that when 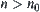 ,
, 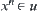 . Then
. Then 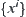 is called to be converging to
is called to be converging to  , denoted by
, denoted by 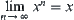 .
.
Definition 2.7.4
Proposition 2.7.6
Assume that 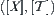 is a quotient topologic space of
is a quotient topologic space of  with respect to R. Then,
with respect to R. Then, 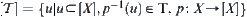 .
.
Definition 2.7.5
For 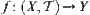 , letting
, letting 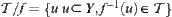 ,
, 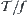 is called the quotient topology of
is called the quotient topology of  with respect to f. We have a topologic space
with respect to f. We have a topologic space 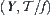 and
and 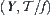 is a congruence space of
is a congruence space of 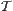 and f.
and f.
Proposition 2.7.7
Proposition 2.7.8
A.3. Separability Axiom
A.3.1. 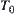 ,
,  ,
, 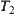 Spaces
Spaces
Definition 3.1.1
Definition 3.1.2
Definition 3.1.3
Proposition 3.1.1
X is a 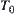 space
space  ,
, 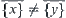 , where
, where 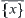 is the closure of singleton
is the closure of singleton 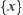 . It means that the closures of any two different singletons are different.
. It means that the closures of any two different singletons are different.
Proposition 3.1.2
(1) X is a  space.
space.
(2) Each singleton on X is a close set.
(3) Each finite set on X is a close set.
Proposition 3.1.3
Proposition 3.1.5
Proposition 3.1.6
3.2. 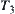 ,
, 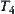 , Regular and Normal Space
, Regular and Normal Space
Definition 3.2.1
In space  ,
, , A is close. For
, A is close. For 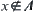 , if there exist open sets
, if there exist open sets  and
and  ,
, 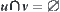 , such that
, such that 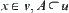 , then X is called a
, then X is called a 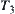 space.
space.
Definition 3.2.2
In space  , for
, for 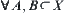 , if there exist open sets
, if there exist open sets  and
and  such that
such that  , then X is called a
, then X is called a 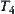 space.
space.
Proposition 3.2.1
Proposition 3.2.2
Proposition 3.2.3
Proposition 3.2.4 (Tietz Theorem)
Definition 3.2.3
If  is a
is a  and
and 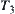 space, then X is called a regular space.
space, then X is called a regular space.
Definition 3.2.4
If  is a
is a  and
and 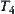 spaces, then X is called a normal space.
spaces, then X is called a normal space.
A.4. Countability Axiom
A.4.1. The First and Second Countability Axioms
Definition 4.1.1
If  has countable base, then X is said to satisfy the second countability axiom.
has countable base, then X is said to satisfy the second countability axiom.
Definition 4.1.2
If in  , for
, for 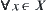 , there exists countable local base, then X is said to satisfy the first countability axiom.
, there exists countable local base, then X is said to satisfy the first countability axiom.
Proposition 4.1.1
Real space R satisfies the second countability axiom.
Proposition 4.1.2
If 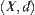 is a metric space, then X satisfies the first countability axiom.
is a metric space, then X satisfies the first countability axiom.
Proposition 4.1.3
If  satisfies the second countability axiom, then X satisfies the first countability axiom.
satisfies the second countability axiom, then X satisfies the first countability axiom.
Proposition 4.1.4
Definition 4.1.3
If  has property P and any sub-space of X also has the property P, property P is called having heredity.
has property P and any sub-space of X also has the property P, property P is called having heredity.
If for  has property P and their product space
has property P and their product space 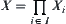 also has property P, then P is called having integrability.
also has property P, then P is called having integrability.
The relation among separation axiom, countability axiom, heredity and integrability is shown in Table 4.1.1.
Table 4.1.1
| Separable | Distance | ||||||||
| heredity | √ | √ | √ | √ | × | √ | √ | × | √ |
| integrability | √ | √ | √ | √ | × | √ | √ | √ | √(countable) |

Where, ![]() and
and ![]() are the first and second countability axioms, respectively.
are the first and second countability axioms, respectively.
√ (countable) means that the product space of the countable number of metric spaces is metrizable.
Proposition 4.1.5
For 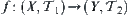 , if X is countable, then f is continuous at
, if X is countable, then f is continuous at 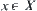
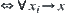 , have
, have 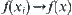 .
.
A.4.2. Separable Space
Definition 4.2.1
If 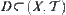 and
and  , then D is called dense in X, or D is a dense subset of X.
, then D is called dense in X, or D is a dense subset of X.
Proposition 4.2.1
Assume that D is a dense subset in  .
. 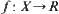 and
and 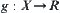 are two continuous mappings. Then,
are two continuous mappings. Then, 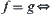
 on D.
on D.
Definition 4.2.2
If  has dense countable subsets, X is called a separable space.
has dense countable subsets, X is called a separable space.
Proposition 4.2.1
If  satisfies
satisfies 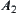 , then X is separable.
, then X is separable.
Proposition 4.2.2
If a separable metric space satisfies 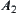 , then it must be
, then it must be  .
.
The relation among  ,
, 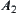 and metric spaces is shown below.
and metric spaces is shown below.


Where, A 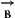 C indicates that property A with the addition of property B infers property C.
C indicates that property A with the addition of property B infers property C.
A.4.3. Lindelof Space
Definition 4.3.1
If a family 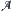 of sets covers B and sub-family
of sets covers B and sub-family 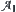 of
of  also covers B, then
also covers B, then  is called a sub-cover of
is called a sub-cover of  .
.
If each set of cover  is open (closed), then
is open (closed), then 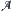 is called an open (closed) cover.
is called an open (closed) cover.
Definition 4.3.2
In  , for any open cover of X, there exists countable sub-cover, X is called a Lindelof space.
, for any open cover of X, there exists countable sub-cover, X is called a Lindelof space.
Proposition 4.3.1
If  satisfies
satisfies 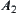 , then X is a Lindelof space.
, then X is a Lindelof space.
Corollary 4.3.1
An n-dimensional Euclidean space 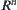 is a Lindelof space.
is a Lindelof space.
Proposition 4.3.2
If 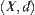 is a Lindelof space, then X satisfies
is a Lindelof space, then X satisfies 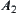 .
.
Proposition 4.3.3
If any sub-space in  is a Lindelof space, then each uncountable subset A of X must have accumulation points of A.
is a Lindelof space, then each uncountable subset A of X must have accumulation points of A.
A.5. Compactness
A.5.1. Compact Space
Definition 5.1.1
In  , if each open cover of X has its finite sub-covers, then X is called a compact space.
, if each open cover of X has its finite sub-covers, then X is called a compact space.
Definition 5.1.2
Assume that 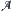 is a family of sets. If each finite sub-family in
is a family of sets. If each finite sub-family in 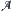 has non-empty intersection, then
has non-empty intersection, then 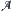 is said to have the finite intersection property.
is said to have the finite intersection property.
Proposition 5.1.1
Proposition 5.1.2
Proposition 5.1.4
If 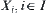 , is compact, then their product space is compact as well.
, is compact, then their product space is compact as well.
A.5.2. Relation between Compactness and Separability Axiom
Proposition 5.2.1
A compact subset in 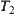 is close.
is close.
Proposition 5.2.2
A compact 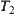 space is a normal space.
space is a normal space.
Proposition 5.2.3
Proposition 5.3.4
Proposition 5.2.5
If 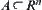 and
and 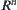 is an n-dimensional Euclidean space, then A is compact
is an n-dimensional Euclidean space, then A is compact 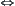 A is a bounded close set.
A is a bounded close set.
Proposition 5.2.6
A.5.3. Some Relations in Compactness
Definition 5.3.1
A topological space  is countably compact if every countable open cover has a finite subcover.
is countably compact if every countable open cover has a finite subcover.
Definition 5.3.2
A topological space  is said to be limit point compact if every infinite subset has a limit point.
is said to be limit point compact if every infinite subset has a limit point.
Definition 5.3.3
A topological space  is sequentially compact if every infinite sequence has a convergent subsequence.
is sequentially compact if every infinite sequence has a convergent subsequence.
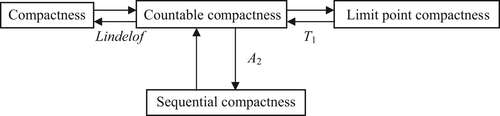

In metric space, especially in n-dimensional Euclidean space, the four concepts of compactness, limit point compactness, countable compactness, and sequential compactness are equivalent.
A.5.4. Local Compact and Paracompact
Definition 5.4.1
In  , for each point on X there exists a compact neighborhood, and X is called a local compact space.
, for each point on X there exists a compact neighborhood, and X is called a local compact space.
Definition 5.4.2
Assume that  and
and  are two covers of X. If each member of
are two covers of X. If each member of 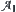 is contained by some member of
is contained by some member of  , then
, then 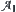 is called the refinement of
is called the refinement of  .
.
Definition 5.4.3
In  ,
, 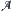 is a cover of subset A. If
is a cover of subset A. If  , there exists
, there exists 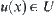 such that
such that 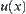 only intersects with the finite number of members in
only intersects with the finite number of members in 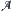 , then
, then 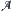 is called a the local finite cover of A.
is called a the local finite cover of A.
Definition 5.4.4
In  , for each open cover of
, for each open cover of 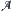 on X, there exists local finite cover
on X, there exists local finite cover 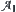 , where
, where 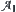 is the refinement of
is the refinement of 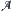 , then X is called a paracompact space.
, then X is called a paracompact space.
Proposition 5.4.1
Each locally compact and 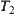 space are normal spaces.
space are normal spaces.
A.6. Connectedness
A.6.1. Connected Space
Definition 6.1.1
Assume that  . If
. If 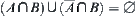 , then
, then 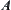 and
and 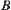 are separate subsets.
are separate subsets.
Definition 6.1.2
In  , if there exist non-empty separate subsets
, if there exist non-empty separate subsets 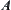 and
and 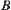 on X such that
on X such that 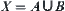 , then X is said to be disconnected. Non-disconnected spaces are called connected spaces.
, then X is said to be disconnected. Non-disconnected spaces are called connected spaces.
Proposition 6.1.1
In  , the following conditions are equivalent.
, the following conditions are equivalent.
(1) X is disconnected
(2) X can be represented by the union of two non-empty and mutually disjoint close sets, i.e., 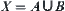 ,
, 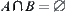 , where
, where 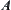 and
and 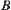 are non-empty close sets
are non-empty close sets
(3) X can be represented by the union of two non-empty and mutually disjoint open sets.
(4) There exists non-empty both open and close proper subset on X.
Definition 6.1.3
For 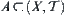 , if A is regarded as a sub-space of X, then it’s connected; A is called a connected subset of X.
, if A is regarded as a sub-space of X, then it’s connected; A is called a connected subset of X.
Proposition 6.1.2
Proposition 6.1.3
Assume that Y is a connected subset on  . If
. If 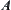 and
and 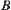 are separate subsets on X,
are separate subsets on X,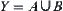 , then
, then 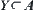 or
or 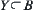 .
.
Proposition 6.1.4
Assume that 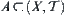 is a connected subset. Let
is a connected subset. Let  . Then, B is a connected subset, especially
. Then, B is a connected subset, especially 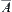 is connected.
is connected.
Proposition 6.1.6
Proposition 6.1.7
If 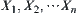 are connected spaces, then their product space
are connected spaces, then their product space 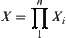 is also connected.
is also connected.
From 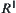 is connected,
is connected, 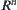 is connected.
is connected.
Proposition 6.1.8
If 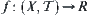 is continuous, X is connected, and there exist
is continuous, X is connected, and there exist 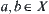 such that
such that 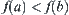 , then for
, then for 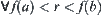 , there must have
, there must have 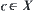 such that
such that 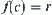 .
.
Proposition 6.1.9
If 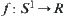 is a continuous mapping, where
is a continuous mapping, where 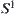 is a unit circle, then there exists
is a unit circle, then there exists 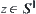 such that
such that 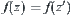 , where
, where  .
.
A.6.2. Connected Component and Local Connectedness
Definition 6.2.1
Assume that  and
and 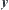 are two points on topologic space
are two points on topologic space  . If there exists a connected set
. If there exists a connected set 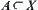 such that
such that 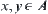 , then
, then  and
and 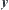 are called connected.
are called connected.
The connected relation among points on  is an equivalence relation.
is an equivalence relation.
Definition 6.2.2
Each equivalent class with respect to connected relations on  is called a connected component of X.
is called a connected component of X.
Definition 6.2.3
For 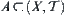 , if A is regarded as a sub-space, its connected component is called a connected component of subset A of X.
, if A is regarded as a sub-space, its connected component is called a connected component of subset A of X.
Definition 6.2.4
In  , for each neighborhood u of
, for each neighborhood u of 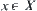 , there exist connected neighborhood
, there exist connected neighborhood  such that
such that 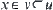 , then X is called local connected at point x. If for
, then X is called local connected at point x. If for 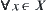
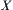 is local connected at x, then X is called a local connected space.
is local connected at x, then X is called a local connected space.
Proposition 6.2.1
(1) If Y is a connected subset on X and 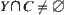 , then
, then 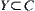 .
.
(2) C is a connected subset.
(3) C is a close set on X.
Proposition 6.2.2
In  , the following statements are equivalent.
, the following statements are equivalent.
(1) X is a local connected space.
(2) Any connected component of any open set of X is open.
(3) There exists a base on X such that its each member is connected.
Proposition 6.2.3
Proposition 6.2.4
If 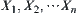 are local connected spaces, then their product space is also local connected.
are local connected spaces, then their product space is also local connected.
Proposition 6.2.5
If 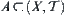 is a connected open set, then A must be a connected component of
is a connected open set, then A must be a connected component of  .
.
A.6.3. Arcwise Connected Space
Definition 6.3.1
If f is an arc on X, then 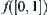 is called a curve on X.
is called a curve on X.
For 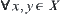 , if there exists an arc
, if there exists an arc 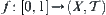 such that
such that 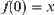 and
and 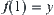 , then X is an arcwise connected space.
, then X is an arcwise connected space.
For 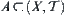 , regarding A as a sub-space, if A is arcwise connected, then A is an arcwise connected subset of X.
, regarding A as a sub-space, if A is arcwise connected, then A is an arcwise connected subset of X.
Definition 6.3.2
For 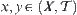 , if there is an arc on X that connects
, if there is an arc on X that connects  and
and 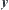 , then
, then  and
and 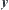 are arcwise connected.
are arcwise connected.
All points on X are an equivalent relation with respect to arcwise connected relations.
Definition 6.3.3
The points on  that belong to an equivalent class with respect to arcwise connected relations are called an arcwise connected component of X.
that belong to an equivalent class with respect to arcwise connected relations are called an arcwise connected component of X.
Proposition 6.3.1
If  is arcwise connected, then X is connected.
is arcwise connected, then X is connected.
Proposition 6.3.2
Proposition 6.3.3
If 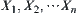 are arcwise connected spaces, then their product space is also an arcwise connected space.
are arcwise connected spaces, then their product space is also an arcwise connected space.
Corollary 6.3.3
Proposition 6.3.4 (Bond Lemma)
Assume that  are close sets and
are close sets and 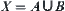 .
. 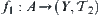 and
and 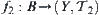 are continuous mappings.
are continuous mappings. 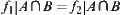 , i.e.,
, i.e., 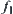 and
and 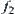 are the same on
are the same on 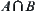 . Let
. Let 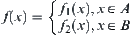 . Then,
. Then, 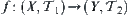 is continuous.
is continuous.
Proposition 6.3.5
For 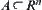 , if A is an open connected set, then A is arcwise connected.
, if A is an open connected set, then A is arcwise connected.
Definition 6.3.4
In  ,
, 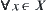 for any neighborhood
for any neighborhood 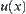 of x, if there exists a connected neighborhood
of x, if there exists a connected neighborhood  such that
such that 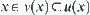 , then X is called local arcwise connected.
, then X is called local arcwise connected.
Proposition 6.3.6
If 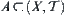 is local arcwise connected and A is connected, then A is arcwise connected.
is local arcwise connected and A is connected, then A is arcwise connected.
Proposition 6.3.7
If  is local arcwise connected and
is local arcwise connected and 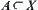 is an open connected subset, then A is arcwise connected.
is an open connected subset, then A is arcwise connected.
Proposition 6.3.8
The continuous image of a local arcwise connected space is also local arcwise connected.
Proposition 6.3.9
If 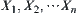 are local arcwise connected, then their product space is also local arcwise connected.
are local arcwise connected, then their product space is also local arcwise connected.
Definition 6.3.5
The above materials are from [Xio81]. The interested readers can also refer to [Eis74].
A.7. Order-Relation, Galois Connected and Closure Space
A.7.1. Order-Relation and Galois Connected
Definition 7.1.1
Assume that ‘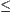 ’ is a binary relation on
’ is a binary relation on  and satisfies reflexivity and transitivity properties, i.e.,
and satisfies reflexivity and transitivity properties, i.e.,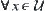 ,
, 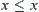 and
and 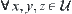 , if
, if 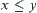 and
and 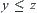 , then
, then 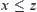 , ‘
, ‘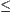 ’ is called a pre-order or quasi-order on
’ is called a pre-order or quasi-order on  .
.
Especially, if ‘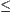 ’ satisfies transitivity and anti-reflexivity, i.e., for
’ satisfies transitivity and anti-reflexivity, i.e., for 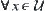 ,
, 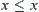 does not hold, then ‘
does not hold, then ‘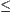 ’ is a strict pre-order on
’ is a strict pre-order on  denoted by ‘
denoted by ‘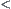 ’ generally.
’ generally.
Definition 7.1.2
If a pre-order relation satisfies anti-symmetry, i.e., 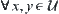 ,
, 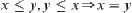 , then
, then 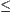 is called a partial order relation on
is called a partial order relation on  .
. 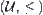 is called a partial ordered set.
is called a partial ordered set.
If a pre-order relation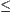 satisfies symmetry, i.e.,
satisfies symmetry, i.e.,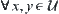 ,
,  , then
, then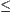 is called an equivalence relation on
is called an equivalence relation on  . Symbol
. Symbol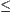 is not used to denote equivalence relations generally.
is not used to denote equivalence relations generally.
Definition 7.1.3
Assume that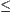 is a semi-order (partial-order) relation on
is a semi-order (partial-order) relation on  . For any two elements
. For any two elements 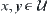 , if their supremum
, if their supremum 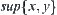 and infimum
and infimum 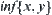 exist, then
exist, then 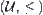 is a lattice. For a lattice
is a lattice. For a lattice 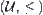 ,
, 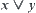 and
and 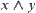 are used to represent the supremum and infimum of two elements
are used to represent the supremum and infimum of two elements  and
and 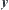 generally.
generally.
Especially, if for any 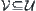 ,
, 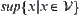 and
and 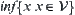 exist, then
exist, then 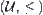 is called a complete lattice.
is called a complete lattice.
Definition 7.1.4
(1) 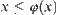 (increasing property)
(increasing property)
(2) 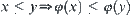 (order-preserving)
(order-preserving)
(3) 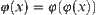 (idempotent)
(idempotent)
Then,  is a closure operator on
is a closure operator on 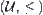 . Correspondingly, if a self-mapping
. Correspondingly, if a self-mapping 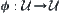 on
on  satisfies order-preserving, idempotent and decreasing property, i.e.,
satisfies order-preserving, idempotent and decreasing property, i.e.,  , then
, then 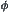 is called an interior operator on
is called an interior operator on 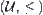 .
.
Note 7.1.1
Note 7.1.2
Assume that  is a closure operator on a complete lattice
is a closure operator on a complete lattice  , where
, where  is any given set and
is any given set and 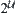 is a power set of
is a power set of  . Then,
. Then,  uniquely corresponds to a family
uniquely corresponds to a family 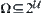 of subsets of
of subsets of  and
and 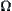 satisfies (1)
satisfies (1) 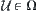 , (2)
, (2) 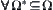 ,
, 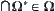 ,
, 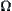 is called a Moore family on
is called a Moore family on  , and two-tuple
, and two-tuple 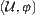 is a closure system.
is a closure system.
Please refer to Davey and Priestley (1992) for more details.
Galois Connection (Davey and Priestley, 1992)
Definition 7.1.5
Assume that 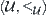 and
and 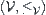 are a pair of semi-order structures.
are a pair of semi-order structures. 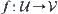 and
and 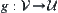 are a pair of mappings. The domains of
are a pair of mappings. The domains of 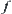 and
and  are
are  and
and 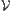 , respectively. If
, respectively. If 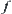 and
and  satisfy
satisfy
For 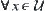 and
and 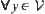 ,
, 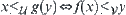 .
.
Then, 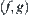 is called a Galois connection between
is called a Galois connection between 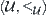 and
and 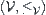 as shown below,
as shown below,
![]()
Proposition 7.1.1
(1) 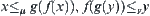
(3) 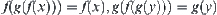
Conversely, assume that 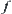 and
and  are a pair of mappings between
are a pair of mappings between 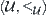 and
and 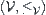 . For
. For 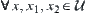 and
and 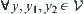 , the above two conditions (1) and (2) hold. Then,
, the above two conditions (1) and (2) hold. Then, 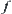 and
and  are a Galois connection between
are a Galois connection between 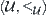 and
and 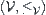 .
.
Proposition 7.1.2
Assume that 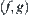 is a Galois connection between
is a Galois connection between 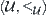 and
and 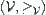 , where
, where 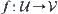 and
and 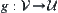 . Then the combination mapping
. Then the combination mapping  is a closure operator on
is a closure operator on 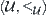 , and
, and 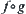 is an interior operator on
is an interior operator on 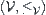 .
.
A.7.2. Closure Operation and Closure Space
The concept of closure operation that we previously introduced is under the order theory sense. The terms of closure operation, closure space and related properties that we will introduce below have the topologic sense, especially under E. Cech sense, i.e., based on set theory and always assuming that there does not appear paradox (Cech, 1966).
Definition 7.2.1
(cl1) 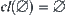
(cl2) 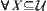 ,
, 
(cl3) 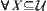 and
and 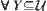 ,
, 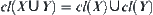
then, Proposition 7.2.1
If 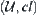 is a closure space, then
is a closure space, then
(1) 
(2) For 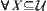 and
and 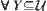 , if
, if 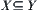 , then
, then 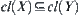
(3) For any family 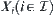 of subsets of
of subsets of  , have
, have 
Definition 7.2.2
![]()
If  holds, then closure operation
holds, then closure operation  is said to be coarser than
is said to be coarser than  . Equivalently,
. Equivalently,  is said to be finer than
is said to be finer than  .
.
Theorem 7.2.1
Binary relation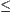 is a semi-order relation on
is a semi-order relation on 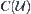 .
. 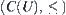 has a greatest element
has a greatest element 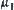 and a least element
and a least element 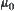 . That is, for
. That is, for  , if
, if 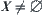 , then
, then 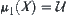 , otherwise
, otherwise 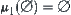 ; and
; and 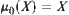 . Furthermore, for any subset
. Furthermore, for any subset 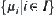 of
of 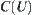 and
and  , we have
, we have  , i.e.,
, i.e., 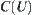 is order complete with respect to
is order complete with respect to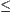 .
.
Definition 7.2.2
![]()
Correspondingly, 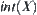 is called
is called 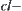 interior of
interior of 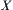 , or simply interior.
, or simply interior.
Proposition 7.2.3
Assume that 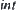
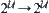 satisfies axioms int1∼ int3. Define an operation
satisfies axioms int1∼ int3. Define an operation 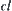 as follows
as follows
![]()
It can be proved that 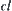 is a closure operation on
is a closure operation on  and
and 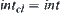 . If
. If 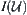 is a set of mappings
is a set of mappings 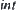 on
on  that satisfy axioms int1∼ int3, then there exists one-one correspondence between
that satisfy axioms int1∼ int3, then there exists one-one correspondence between 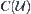 and
and 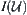 . Or a closure operation and an interior operation are dual.
. Or a closure operation and an interior operation are dual.
Definition 7.2.3
Proposition 7.2.4
(2) For 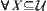 and
and 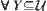 , if
, if 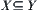 , then
, then 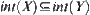 .
.
(3) For any family 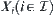 of subsets of
of subsets of  , have
, have 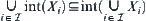
Definition 7.2.4
A topological closure operation on  is a closure operation
is a closure operation 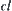 that satisfies the following condition
that satisfies the following condition
![]()
If 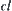 is a topological closure operation, then closure space
is a topological closure operation, then closure space 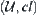 is a topological space.
is a topological space.
Proposition 7.2.5
If 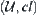 is a closure space, then each condition shown below is the necessary and sufficient condition that
is a closure space, then each condition shown below is the necessary and sufficient condition that 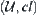 is a topological space.
is a topological space.
(1) The closure of each subset is a close set
(2) The interior of each subset is an open set
(3) The closure of each subset equals to the intersection of all close sets that include the subset
(4) The interior of each subset equals to the union of all open sets that include the subset.
Theorem 7.2.2
Assume that 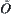 is a family of subsets of set
is a family of subsets of set  that satisfies the following conditions
that satisfies the following conditions
(o1)  ,
, 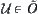
(o2) 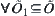 ,
,  , i.e.,
, i.e., 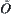 is closed for any union operation
is closed for any union operation
(o3) 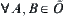 ,
, 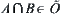 , i.e.,
, i.e., 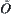 is closed for finite intersection operation.
is closed for finite intersection operation.
Let 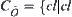 is a closure operation on
is a closure operation on  and the set composed by all open sets of
and the set composed by all open sets of 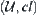 is just
is just  .
.
Then, there just exists a topological closure operation  on
on 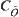 such that
such that  is the roughest element on
is the roughest element on 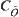 .
.
Theorem 7.2.3
Assume that 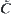 is a family of subsets of set
is a family of subsets of set  that satisfies the following conditions
that satisfies the following conditions
(c1) 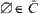 ,
, 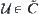
(c2)  ,
, 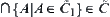 , i.e.,
, i.e., 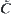 is closed for any union operation
is closed for any union operation
(c3) 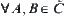 ,
,  , i.e.,
, i.e., 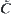 is closed for finite intersection operation.
is closed for finite intersection operation.
Then, there just exists a topological closure operation  on
on  such that
such that 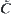 is just a set that composed by all close sets on
is just a set that composed by all close sets on 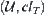 .
.
Using open set as a language to describe topology, axioms (o1) ∼ (o3) are used. However, conditions (cl1) ∼ (cl4) are called axioms of Kuratowski closure operator. Kuratowski closure operator, interior operator that satisfies axioms (int1) ∼ (int3) and (int4):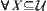
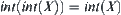 , open set and neighborhood system are equivalent tools for describing topology. For describing non-topologic closure spaces, only closure operations, interior operations and neighborhood systems can be used, but open set or close set cannot be used as a language directly. In some sense, closure spaces are more common than topologic spaces. We will discuss continuity, connectivity and how to construct a new closure space from a known one below.
, open set and neighborhood system are equivalent tools for describing topology. For describing non-topologic closure spaces, only closure operations, interior operations and neighborhood systems can be used, but open set or close set cannot be used as a language directly. In some sense, closure spaces are more common than topologic spaces. We will discuss continuity, connectivity and how to construct a new closure space from a known one below.
A closure operation 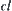 on a domain set
on a domain set  is defined as a mapping from
is defined as a mapping from 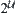 to itself, where domain
to itself, where domain 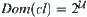 and codomain
and codomain 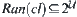 . Closure operation
. Closure operation 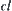 is completely defined by binary relation
is completely defined by binary relation 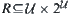 , i.e.,
, i.e., 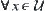 and
and 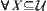 ,
, 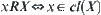 . Obviously, we have
. Obviously, we have 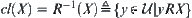 .
.
Compared to 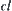 , relation
, relation  more clearly embodies the intuitive meaning of closure operation, i.e., what points are proximal to what sets. Naturally, the intuitive meaning of continuous mappings is the mapping that remains the ‘
more clearly embodies the intuitive meaning of closure operation, i.e., what points are proximal to what sets. Naturally, the intuitive meaning of continuous mappings is the mapping that remains the ‘ is proximal to subset
is proximal to subset 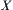 ’ relation.
’ relation.
Definition 7.2.5
Theorem 7.2.4
(1) f is a continuous mapping
(2) For 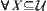 ,
, 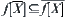 holds.
holds.
(3) For 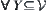 ,
, 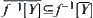 holds.
holds.
Definition 7.2.6
Definition 7.2.7
If there exists a homeomorphous mapping from closure space  to
to 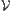 , then
, then  and
and 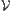 are called homeomorphous closure spaces.
are called homeomorphous closure spaces.
Definition 7.2.8
If a closure space  has property
has property 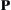 such that all spaces that homeomorphous to
such that all spaces that homeomorphous to  have the property, then
have the property, then 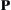 is called the topological property.
is called the topological property.
Obviously, the homeomorphous relation is an equivalent relation on the set composed by all closure spaces.
Definition 7.2.9
Definition 7.2.10
Below we will discuss how to generate a new closure operation from a known closure operation, or a set of closure operations. Two generated approaches are discussed, the generated projectively and generated inductively. The product topology and quotient topology discussed in point topology are special cases of the above two generated approaches in closure operation.
Definition 7.2.11
![]()
The above closure operation is the finest one among all closure operations that make 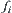 continuous.
continuous.
The closure operation on 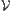 generated inductively by a set
generated inductively by a set  of mappings is defined as follows
of mappings is defined as follows
![]()
The above closure operation is the finest one among all closure operations that make each 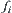 ,
, 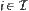 continuous.
continuous.
Proposition 7.2.6
Definition 7.2.12
![]()
The above closure operation is the coarsest one among all closure operations that make 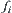 continuous. The closure operation on
continuous. The closure operation on 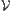 generated projectively by a set
generated projectively by a set  of mappings is defined by
of mappings is defined by 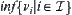 . It is the coarsest one among all closure operations that make each
. It is the coarsest one among all closure operations that make each 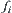 ,
, 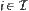 continuous.
continuous.
Note that 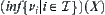 is not necessarily the
is not necessarily the 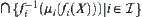 . And the latter is not necessarily a closure operation, unless a set
. And the latter is not necessarily a closure operation, unless a set 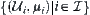 of closure spaces satisfies a certain condition (Cech, 1966).
of closure spaces satisfies a certain condition (Cech, 1966).
A.7.3. Closure Operations Defined by Different Axioms
Two forms of closure that we mentioned previously are denotes by closure operator and closure operation, respectively. The former is under order theory sense and the latter is under topologic sense. In fact, the term of closure does not have a uniform definition. In different documents it might have different meanings. We introduce different definitions of closure, quasi-discrete closure space, Allexandroff topology, etc. below.
Table 7.3.1
| (CL0) | (CL1) | (CL2) | (CL3) | (CL4) | (CL5) | |
| Neighborhood space | ♦ | ♦ | ♦ | |||
| Closure space | ♦ | ♦ | ♦ | ♦ | ||
| Smith space | ♦ | ♦ | ♦ | |||
| Cech closure space | ♦ | ♦ | ♦ | ♦ | ||
| Topological space | ♦ | ◊ | ♦ | ♦ | ♦ | |
| Alexandroff space | ♦ | ◊ | ♦ | ◊ | ♦ | |
| Alexandroff topology | ♦ | ◊ | ♦ | ◊ | ♦ | ♦ |
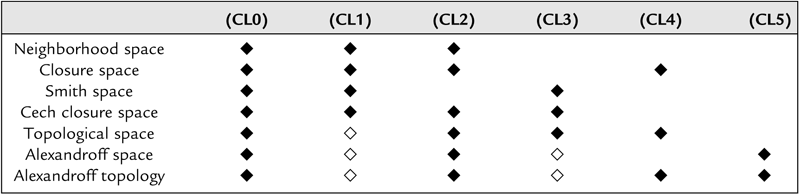
♦: the axiom satisfied by definition ◊: the property induced by definition.
Using the dual interior operation  of
of 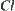 , we have the following equivalent axioms (CL0)∼(CL5). For
, we have the following equivalent axioms (CL0)∼(CL5). For 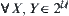 , we have
, we have
Note 7.3.1
Under the general order theory sense, the closure space is defined by axioms (CL1), (CL2) and (CL4). For example, the closure operation defined by Definition 7.1.4 is called closure operator. When considering the inclusion relation between a power set and a subset, the axiom (CL0) may be or may not be satisfied.
Note 7.3.2
Under the Cech’s sense, the closure space is called pre-topology and is defined by axioms (CL0)∼(CL3). In Definition 7.1.4, axioms (CL0) and (CL3) are replaced by (CL3)’. The topology described by the Kuratowski closure operator that satisfies axioms (CL0), (CL2), (CL3)’ and (CL4) is equivalent to the above description, since axiom (CL3)’ may induce axiom (CL3), and (CL4)+(CL3) may induce (CL3)’. The distinction between the closure space in the Cech’s sense and the topologic space in general sense is the satisfaction of the idempotent axiom or not. So the former is the extension of the latter.
Note 7.3.3
Axiom (CL5) is called Alexandroff property. The topologic space that satisfies the Alexandroff property is called Alexandroff topology. In Cech (1966) and Galton (2003), axiom (CL5) is called quasi-discrete property. The Cech closure space that satisfies quasi-discrete property is called quasi-discrete closure space.
Note 7.3.4
To describe the closure space, except closure and interior operations, the neighborhood and the filter convergent sequence can be used equivalently. In Table 7.3.1, the neighborhood and Smith spaces (Kelly, 1955; Smith, 1995) originally are described by neighborhood language; we use the equivalent closure axioms.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.

