.1.2. World Representations at Different Granularities
1.2.1. The Model of Different Grain-Size Worlds
From the above discussion, it seems important to develop a new theory and technique which will in some way enable computers to represent the world at different granularities.
Suppose that a problem-solving space, or a problem space for short, is described by a triplet .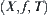
.X denotes the problem domain, or universe. In the preceding example, when drafting a production plan, the factory as a whole is the domain in question.
indicates the attributes of domain X or is denoted by a function 
, where Y may be a real set, a set of n-dimensional space 
, or a general space, 
is either single-valued or multi-valued. For each element 
corresponds to a certain attribute of the x, and is called an attribute function. In the example above, value of output, work-force and profit are the attributes that depict the factory.T is the structure of domain X, i.e. the relations among elements in X. For example, the relations among workshops, workers, machines and managers, etc. Structure T is the most complex and various part of the triplet description. One main category includes the Euclidean distance in Euclidean space, the inner product in inner product space, the metric in metric space, the semi-order in semi-order space, topology in topological space, directed graphs and undirected graphs, etc. The other is the structure that arose from some operations such as linear space, group, ring, field and lattice in algebra and logic inference. Certainly, the above two categories may be combined to form a new structure, for example, normed space, normed ring, etc.
Given a problem space 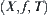, solving a problem implies the analysis and investigation of X, f and T. But the problems are how to choose a suitable granularity of X, what relationships exist among different grain size worlds, etc.
, solving a problem implies the analysis and investigation of X, f and T. But the problems are how to choose a suitable granularity of X, what relationships exist among different grain size worlds, etc.Suppose that X indicates a domain with the finest grain-size. By simplifying X we have a more coarse-grained domain denoted by 
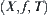. So the original problem space is transformed into a new one 
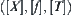with a new abstraction level. In the above ‘factory’ example, if groups are elements of domain X, then, in a simplified domain , its elements may be sections, each consists of several groups, i.e., the elements with common or similar functions in X as shown in Fig. 1.3.
. So the original problem space is transformed into a new one with a new abstraction level. In the above ‘factory’ example, if groups are elements of domain X, then, in a simplified domain , its elements may be sections, each consists of several groups, i.e., the elements with common or similar functions in X as shown in Fig. 1.3.
The hierarchical structure shown in Fig. 1.3 is quite similar to the concept of quotient set in mathematics (Eisenberg, 1974).
Assume that X is a domain, R is an equivalence relation on X, and is a quotient set under R. Regarding as a new domain, we have a new world which is coarser than X. We say that X is classified with respect to R.
is a quotient set under R. Regarding as a new domain, we have a new world which is coarser than X. We say that X is classified with respect to R.Before the discussion of the domain partition, we first introduce some concepts and propositions of set theory.
Definition 1.1
Assume that X and Y are two sets,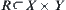 
is a product set of X and Y on 
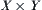. For 
, have 
. We say that x and y have relation R denoted as 
, or R is a relation on . When 
, R is called a relation on X.
is a product set of X and Y on . For 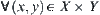, have 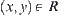. We say that x and y have relation R denoted as 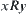, or R is a relation on 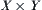. When 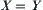, R is called a relation on X.Definition 1.2
Assume that X is a set, R is a relation on X and satisfies
(1) Reflexivity: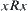 
,
,(2) Symmetry: if 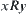, then 
,
, then 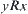,(3) Transitivity: If 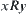and 
, then 
,
and 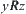, then 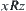,R is called an equivalence relation on X denoted by 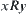or 
.
or .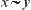
Definition 1.4
is a quotient set of X under R.Namely, quotient set 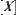becomes a new set by regarding 
as its elements.
becomes a new set by regarding 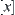as its elements.From the previous discussion, it is known that the different grain-size world and the concept of quotient set in mathematics are unified or quotient sets can be regarded as a mathematical model of domains of the different grain-size world.
Different grain-size world model: To investigate problem 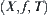from different granularities (angles, or abstraction levels) means inspecting the corresponding problem , where [X] is a quotient set of X under equivalence relation R, [f] and [T] are the quotient attribute and quotient structure on [X], respectively. is a quotient space of . Different quotient sets of X correspond to different quotient spaces which compose different grain-size worlds of problem . Quotient space theory is used to investigate the representations and properties of domains, attributes and structures of a problem space under different granularities, and their interdependent and transformational relations.
from different granularities (angles, or abstraction levels) means inspecting the corresponding problem 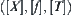, where [X] is a quotient set of X under equivalence relation R, [f] and [T] are the quotient attribute and quotient structure on [X], respectively. 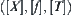is a quotient space of 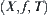. Different quotient sets of X correspond to different quotient spaces which compose different grain-size worlds of problem 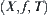. Quotient space theory is used to investigate the representations and properties of domains, attributes and structures of a problem space under different granularities, and their interdependent and transformational relations.Definition 1.5
If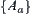 
is a partition of X ⇔ (1) 
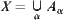, (2) if 
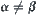then 
, where 
is a subset of X.
is a partition of X ⇔ (1) , (2) if then 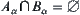, where 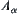is a subset of X.Proposition 1.1
If R is an equivalence relation on X, then 
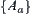is a partition of X. Conversely, giving a partition on X, an equivalence relation R on X is uniquely defined. A set of equivalence classes of X corresponding to R is .
is a partition of X. Conversely, giving a partition on X, an equivalence relation R on X is uniquely defined. A set of equivalence classes of X corresponding to R is 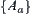.From the above proposition, it is known that different grain-size representations of a problem correspond to different equivalence relations or different partitions. In a factory, if we consider machining as an equivalence class called a workshop, then turning, milling and bench work sections belong to the same workshop. They are included in the same equivalence class, whereas in a fine-grained model, turning, milling and bench work may be regarded as different elements (see Fig. 1.3).
1.2.2. The Definition of Quotient Space
In summary, when a problem 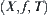and an equivalence relation R are given, we define a quotient space as follows:
and an equivalence relation R are given, we define a quotient space 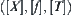as follows:
Then, we have a new problem 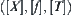, that is, a new abstraction level of the original problem . Each R corresponds to a certain grain-size world.
, that is, a new abstraction level of the original problem 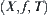. Each R corresponds to a certain grain-size world...................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.