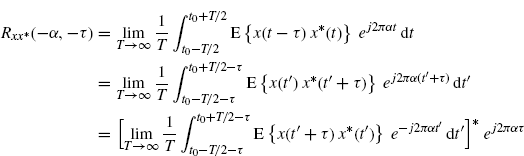3.1 Proofs for Section 2.2.2 “Second-Order Wide-Sense Statistical Characterization”

3.1.1 Proof of Theorem 2.2.17 Mean-Square Integrability of GACS Processes

By substituting t + τ = t₁, t = t₂ into (2.18) we have

(3.1)

Thus

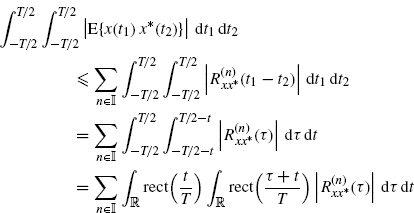
(3.2)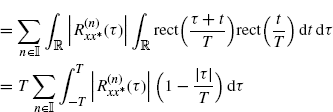

where, in the first equality the variable changes t₁ = t + τ and t₂ = t are made, and in the last equality the result

(3.3)

is used. Thus, accounting for Assumption 2.2.16, the sufficient condition of Theorem 2.2.15 turns out to be satisfied.

3.1.2 Proof of Fact 2.2.18

(3.4)

where, in the second equality, the variable change t′ = t − τ is made. (3.4) is equivalent to (2.52) from which (2.54) follows.

From (2.54) we have

(3.5)

(3.6)

Therefore, (2.55) follows. In addition, one has

(3.7)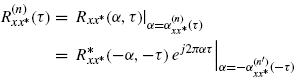

which is equivalent to (2.56).

3.1.3 Proof of Fact 2.2.19

(3.8)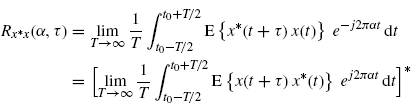

from which we obtain (2.57). From (2.57) it follows that

(3.9)

Therefore

(3.10)

from which we have (2.58) In addition, one has

(3.11)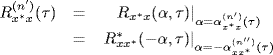

which leads to (2.59).

3.1.4 Proof of Fact 2.2.20

(3.12)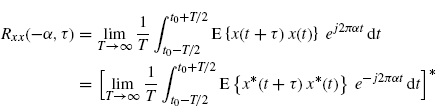

from which we obtain (2.60). From (2.60) it follows that

(3.13)

Therefore

(3.14)

from which we have (2.61). In addition, one has

(3.15)

which leads to (2.62).