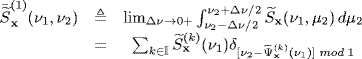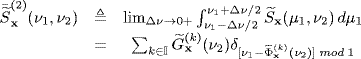4.9 Sampling of SC Processes
In this section, a sampling theorem for SC processes is stated to link the Loève bifrequency spectrum of the sampled discrete-time process with that of the continuous-time process. An analogous result is established in terms of densities. Furthermore, in the case of strictly band-limited continuous-time SC processes, sufficient conditions on the sampling frequency to avoid aliasing effects are provided (Napolitano 2011).
For a WSS process, two equivalent conditions describe the absence of aliasing in the Loève bifrequency spectrum of the sampled signal. The former is the non overlap of replicas in the power spectrum of the sampled signal (Lloyd 1959). The latter is that the mappings νi = fi/fs, i = 1, 2, between frequencies fi ![]() [− fs/2, fs/2] of the density of Loève bifrequency spectrum of the continuous-time process and frequencies νi of the density of Loève bifrequency spectrum of the discrete-time process hold ∀ν1
[− fs/2, fs/2] of the density of Loève bifrequency spectrum of the continuous-time process and frequencies νi of the density of Loève bifrequency spectrum of the discrete-time process hold ∀ν1 ![]() [− 1/2, 1/2], on the main diagonal ν2 = ν1. In fact, on the main diagonal the density of Loève bifrequency spectrum is coincident with the power spectrum. It is well known that both conditions are satisfied provided that the sampling frequency is equal to or greater than twice the process bandwidth. In this section it is shown that for SC processes, unlike the case of WSS processes, a sampling frequency equal to twice the signal bandwidth is not sufficient to assure that the mappings νi = fi/fs hold for the density on every support curve ∀ν1
[− 1/2, 1/2], on the main diagonal ν2 = ν1. In fact, on the main diagonal the density of Loève bifrequency spectrum is coincident with the power spectrum. It is well known that both conditions are satisfied provided that the sampling frequency is equal to or greater than twice the process bandwidth. In this section it is shown that for SC processes, unlike the case of WSS processes, a sampling frequency equal to twice the signal bandwidth is not sufficient to assure that the mappings νi = fi/fs hold for the density on every support curve ∀ν1 ![]() [− 1/2, 1/2] (or ∀ν2
[− 1/2, 1/2] (or ∀ν2 ![]() [− 1/2, 1/2]). A sufficient condition is derived on the sampling frequency to assure that these mappings hold and known results for ACS processes (Napolitano 1995), (Izzo and Napolitano 1996), (Gardner et al. 2006) are obtained as special cases.
[− 1/2, 1/2]). A sufficient condition is derived on the sampling frequency to assure that these mappings hold and known results for ACS processes (Napolitano 1995), (Izzo and Napolitano 1996), (Gardner et al. 2006) are obtained as special cases.
It is worth underlining that the problem of avoiding aliasing in the spectral correlation density of the sampled process should not be confused with the problem of signal reconstruction from its samples. This latter problem is addressed, for example, in (Lloyd 1959) for stationary processes and in (Gardner 1972), (Lee 1978) for nonstationary processes. In (Lloyd 1959), for stationary processes it is shown that the lack of overlap of replicas in the bifrequency Loève spectrum of the sampled process is a necessary and sufficient condition to allow the continuous-time process reconstruction with appropriate sense of convergence. In the case of base-band signals, this condition is the classical Shannon condition on the sampling frequency. In (Lee 1978), it is shown that for nonstationary processes such a condition is only sufficient. Finally, note that the class of processes considered here, namely the SC and ACS processes, have sample paths that are finite-power functions. Thus, known results for ![]() functions (Garcia et al. 2001), (Song et al. 2007) or
functions (Garcia et al. 2001), (Song et al. 2007) or ![]() functions cannot be exploited.
functions cannot be exploited.
4.9.1 Band-Limitedness Property
It is well known that for WSS processes the strictly band-limitedness condition allows one to avoid aliasing after uniform sampling, provided that the sampling frequency exceeds twice the process bandwidth. Nonstationary processes should be carefully handled. In particular, not every nonstationary structure is compatible with the band-limitedness property. ACS processes can be strictly band limited (Gardner et al. 2006). In contrast, in Sections 2.2.2 and 2.2.3 (see also (Napolitano 2007a) and (Napolitano 2009)) it is shown that GACS processes cannot be strictly band limited. In the sequel it is proved that SC processes can be strictly band limited (Napolitano 2011). For this purpose, a definition of strict band limitedness is given for the general case of nonstationary processes. Specifically, a nonstationary process is said to be strictly band limited when it passes unaltered through an ideal strictly band-limited filter.
Let h(b)(t) be the impulse response function of the ideal low-pass filter with harmonic response H(b)(f) = rect(f/2b).
Definition 4.9.1 A continuous-time nonstationary stochastic process xa(t) is said to be (almost-surely) strictly band limited with bandwidth B if B is the infimum of the values of b such that
almost surely (a.s.) ∀t, where ⊗ denotes convolution. ![]()
If xa(t) is a second-order process, then (4.204) holding a.s. ∀t is equivalent to
(4.205) ![]()
The condition of Definition 4.9.1 can be relaxed by requiring that (4.204) holds for almost all t. If (4.204) is satisfied, it follows that (see (5.179) in Section 5.10)
which is the band-limitedness condition for nonstationary processes considered in (Gardner 1972). Such a condition can also be obtained by following (Lii and Rosenblatt 2002) in terms of the spectral measure ![]() which is a set function (Hurd and Miamee 2007). Let A be a Borel subset of
which is a set function (Hurd and Miamee 2007). Let A be a Borel subset of ![]() . The process xa(t) is strictly band limited in [− B, B] if
. The process xa(t) is strictly band limited in [− B, B] if
(4.207) ![]()
If (4.206) holds, in (Gardner 1972) it is shown that for a sampling period Ts < 1/(2B) the process xa(t) admits the mean-square equivalent “sample representation”
(4.208) ![]()
where sinc(t) ![]() sin(πt)/(πt). Further band-limitedness definitions for nonstationary processes are considered in (Zakai 1965), (Cambanis and Masry 1976).
sin(πt)/(πt). Further band-limitedness definitions for nonstationary processes are considered in (Zakai 1965), (Cambanis and Masry 1976).
In Sections 2.2.2 and 2.2.3 it is shown that GACS processes cannot be strictly band limited (see also (Izzo and Napolitano 2002a) and (Izzo and Napolitano 2002b)). In contrast, for the SC processes the following results hold.
Let xa,i(t), (i = 1, 2), be continuous-time jointly SC processes with Loève bifrequency cross-spectrum
where ![]() .
.
Theorem 4.9.2 Strictly Band-Limited Spectrally Correlated Processes (Napolitano 2011, Theorem 2.1). Let xa,i(t), (i = 1, 2), be jointly SC processes with Loève bifrequency cross-spectrum (4.209a), (4.209b). If the processes are strictly band-limited with bandwidths Bi and if the points of the intersections of the support curves are non-dense (in the meaning assumed in the proof), the result is that ![]()
Moreover, the functions ![]() and
and ![]() can be suitably modified so that (4.210a) and (4.210b) hold everywhere since with this modification the cross-correlation (4.24b) (with
can be suitably modified so that (4.210a) and (4.210b) hold everywhere since with this modification the cross-correlation (4.24b) (with ![]() and (4.209a) or (4.209b) substituted into) remains unaltered. In addition,
and (4.209a) or (4.209b) substituted into) remains unaltered. In addition, ![]() and
and ![]() can be assumed to be zero for f16
can be assumed to be zero for f16 ![]() [− B1, B1] and f26
[− B1, B1] and f26 ![]() [− B2, B2], respectively. In this case,
[− B2, B2], respectively. In this case, ![]() is considered to be invertible from the support of
is considered to be invertible from the support of ![]() to the support of
to the support of ![]() for each
for each ![]() .
.
Conversely, if at least one of (4.210a) or (4.210b) holds, then also the other one holds and the processes xa,i(t) are strictly band-limited with bandwidth Bi.
Proof: See Section 5.10. ![]()
Corollary 4.9.3 Support of the Spectral Cross-Correlation Density Functions (Napolitano 2011, Corollary 2.1). Let xa,i(t), (i = 1, 2), be strictly band-limited jointly SC processes with bandwidths Bi. In the expressions of the Loève bifrequency cross-spectrum (4.209a), (4.209b)![]() it results that
it results that
(4.211a) 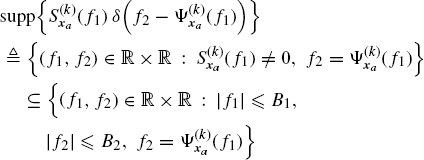
(4.211b) 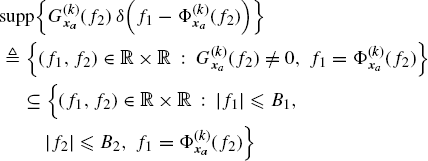
where supp means support. ![]()
4.9.2 Sampling Theorems
Theorem 4.9.4 Loève Bifrequency Cross-Spectrum of Sampled Jointly Spectrally Correlated Processes (Napolitano 2011, Theorem 4.1). Let xa,i(t), (i = 1, 2), be continuous-time jointly SC processes with Loève bifrequency cross-spectrum (4.209a), (4.209b) and let
be the discrete-time processes obtained by uniformly sampling xa,i(t) with sampling periods Tsi ![]() 1/fsi. The processes xi(n) are discrete-time jointly SC with Loève bifrequency cross-spectrum given by
1/fsi. The processes xi(n) are discrete-time jointly SC with Loève bifrequency cross-spectrum given by
and the bounded variation condition (4.183) specializes to
Proof: See Section 5.10. ![]()
By comparing (4.213) with (4.209a) it follows that the Loève bifrequency cross-spectrum of the discrete-time signals is constituted by replicas of that of the continuous-time signals. In addition, according to Theorem 4.9.19, it follows that the discrete-time processes xi(n) are jointly SC. In fact, their Loève bifrequency cross-spectrum exhibits spectral masses concentrated on a countable set of support curves and is periodic with period 1 in both variables ν1 and ν2, even if in general the functions ![]() and
and ![]() of Theorem 4.8.17 cannot be easily expressed in terms of
of Theorem 4.8.17 cannot be easily expressed in terms of ![]() and
and ![]() . Furthermore, at every point (ν1, ν2)
. Furthermore, at every point (ν1, ν2) ![]() [− 1/2, 1/2)2, nonzero contribution to the Loève bifrequency cross-spectrum is given by the terms in (4.213) such that
[− 1/2, 1/2)2, nonzero contribution to the Loève bifrequency cross-spectrum is given by the terms in (4.213) such that
(4.215) ![]()
and
(4.216) ![]()
for some ![]() . Specifically, the support curves in the bifrequency principal domain (ν1, ν2)
. Specifically, the support curves in the bifrequency principal domain (ν1, ν2) ![]() [− 1/2, 1/2)2 are described by the set
[− 1/2, 1/2)2 are described by the set
(4.217) 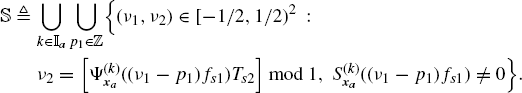
In general, aliasing effects are present. The set ![]() can contain clusters of curves or can be dense in the square [− 1/2, 1/2)2 if, for some ν1
can contain clusters of curves or can be dense in the square [− 1/2, 1/2)2 if, for some ν1 ![]() [− 1/2, 1/2), fs2 is incommensurate with a countable infinity of values of
[− 1/2, 1/2), fs2 is incommensurate with a countable infinity of values of ![]() ,
, ![]() ,
, ![]() , and in correspondence of these values the spectral densities
, and in correspondence of these values the spectral densities ![]() are nonzero. In such a case,
are nonzero. In such a case, ![]() is non identically zero for |f1| > B for some B.
is non identically zero for |f1| > B for some B.
In the special case of support lines ![]() , single sampling frequency fs1 = fs2 = fs, and if frequencies ν1 are evaluated on the bins of a N-point discrete Fourier transform (DFT), that is, ν1 = n1/N, n1 = − N/2, …, (N − 1)/2, (N even), then
, single sampling frequency fs1 = fs2 = fs, and if frequencies ν1 are evaluated on the bins of a N-point discrete Fourier transform (DFT), that is, ν1 = n1/N, n1 = − N/2, …, (N − 1)/2, (N even), then
(4.218) ![]()
Thus, if ![]() is infinite and a(k) is irrational and/or b(k)/fs is irrational for some k, then the restriction of
is infinite and a(k) is irrational and/or b(k)/fs is irrational for some k, then the restriction of ![]() to ν1 = n1/N is dense (in ν2) due to the presence of clusters of lines in
to ν1 = n1/N is dense (in ν2) due to the presence of clusters of lines in ![]() , provided that the spectral density
, provided that the spectral density ![]() is not identically zero for |f1| > B, for some B. In (Lii and Rosenblatt 2002), only condition a(k) irrational is considered since the special case of
is not identically zero for |f1| > B, for some B. In (Lii and Rosenblatt 2002), only condition a(k) irrational is considered since the special case of ![]() finite is treated, so that only the term a(k)p1fs can make the set
finite is treated, so that only the term a(k)p1fs can make the set ![]() dense when a(k) is irrational and
dense when a(k) is irrational and ![]() .
.
In (Lii and Rosenblatt 2002), it is explained that the aliasing problem (in the sense of spectral mass folding onto [− 1/2, 1/2]2) is a consequence of the relationship (see also (5.185))
(4.219) ![]()
This aliasing effect is illustrated in the numerical experiments in (Lii and Rosenblatt 2002), (Napolitano 2010b) and Section 4.9.3.
Theorem 4.9.5 Loève Bifrequency Cross-Spectrum of Sampled Strictly Band-Limited Jointly SC Processes (Napolitano 2011, Theorem 4.2). Let xa,i(t), i = 1, 2, be continuous-time jointly SC processes with Loève bifrequency cross-spectrum (4.209a), (4.209b) strictly band-limited with bandwidths Bi and functions ![]() invertible. If fsi ≥ 2Bi, then the processes xi(n) defined in (4.212) are discrete-time jointly SC having Loève bifrequency cross-spectrum (4.190a) and (4.190b) with
invertible. If fsi ≥ 2Bi, then the processes xi(n) defined in (4.212) are discrete-time jointly SC having Loève bifrequency cross-spectrum (4.190a) and (4.190b) with
and all periodic functions (4.220a)–(4.221b) are sums of nonoverlapping replicas. In such a case, the bounded variation condition (4.214) is equivalent to the bounded variation condition for the continuous-time processes (4.18). Moreover, if ![]() and
and ![]() are also differentiable, then the assumptions for Theorem 4.8.3 are verified and (4.191a) and (4.191b) hold.
are also differentiable, then the assumptions for Theorem 4.8.3 are verified and (4.191a) and (4.191b) hold.
Proof: See Section 5.10. ![]()
The support function ![]() and the corresponding spectral correlation density
and the corresponding spectral correlation density ![]() are said to be exactly identifiable starting from the samples (4.212) if and only if the equalities
are said to be exactly identifiable starting from the samples (4.212) if and only if the equalities
hold ∀ν1 ![]() [− 1/2, 1/2]. Under the assumption fsi ≥ 2Bi of Theorem 4.9.20, the relationships (4.222) and (4.223) hold only for
[− 1/2, 1/2]. Under the assumption fsi ≥ 2Bi of Theorem 4.9.20, the relationships (4.222) and (4.223) hold only for ![]() which, in general, is a proper subset of [− 1/2, 1/2], where suppc means “support curve of”. Analogously,
which, in general, is a proper subset of [− 1/2, 1/2], where suppc means “support curve of”. Analogously,
hold only for ![]() which, in general, is a proper subset of [− 1/2, 1/2]. Thus, for (jointly) SC processes, (4.222), (4.223) defined by the mapping ν1 = f1/fs1 do not hold for every support curve ∀ν1
which, in general, is a proper subset of [− 1/2, 1/2]. Thus, for (jointly) SC processes, (4.222), (4.223) defined by the mapping ν1 = f1/fs1 do not hold for every support curve ∀ν1 ![]() [− 1/2, 1/2] and (4.224), (4.225) defined by the mapping ν2 = f2/fs2 do not hold for every support curve ∀ν2
[− 1/2, 1/2] and (4.224), (4.225) defined by the mapping ν2 = f2/fs2 do not hold for every support curve ∀ν2 ![]() [− 1/2, 1/2]. In contrast, for (jointly) WSS processes, spectral masses are present only on the main diagonal of the bifrequency plane and condition fsi ≥ 2Bi assures that (4.222)–(4.225) defined by the mappings νi = fi/fsi hold for the unique support line and the corresponding density ∀νi
[− 1/2, 1/2]. In contrast, for (jointly) WSS processes, spectral masses are present only on the main diagonal of the bifrequency plane and condition fsi ≥ 2Bi assures that (4.222)–(4.225) defined by the mappings νi = fi/fsi hold for the unique support line and the corresponding density ∀νi ![]() [− 1/2, 1/2], i = 1, 2.
[− 1/2, 1/2], i = 1, 2.
By considering a more stringent condition on the sampling frequencies, (4.222)–(4.225) determined by the νi ↔ fi mappings can be made valid for every support curve ∀νi ![]() [− 1/2, 1/2], i = 1, 2. We have the following result.
[− 1/2, 1/2], i = 1, 2. We have the following result.
Theorem 4.9.6 Density of Loève Bifrequency Cross-Spectrum of Sampled Strictly Band-Limited Jointly SC Processes (Napolitano 2011, Theorem 4.3). Let xa,i(t), i = 1, 2, be continuous-time jointly SC processes with Loève bifrequency cross-spectrum (4.209a), (4.209b) and let the processes be strictly band limited with bandwidths Bi. If
then conditions (4.222) and (4.223) hold ∀ν1 ![]() [− 1/2, 1/2]. Analogously, if
[− 1/2, 1/2]. Analogously, if
then conditions (4.225) and (4.225) hold ∀ν2 ![]() [− 1/2, 1/2].
[− 1/2, 1/2].
Proof: See Section 5.10. ![]()
For ![]() and
and ![]() strictly increasing or decreasing functions, the sup over ν1 and ν2 in (4.226) and (4.227) are achieved for νi equal to 1/2 or −1/2.
strictly increasing or decreasing functions, the sup over ν1 and ν2 in (4.226) and (4.227) are achieved for νi equal to 1/2 or −1/2.
If the sufficient conditions (4.226) and (4.227) are satisfied then, accounting for (4.222)–(4.225), support curves and cross-spectral densities of the continuous-time signals can be reconstructed from those of the discrete-time signals by the frequency rescalings ν1 = f1/fs1 and ν2 = f2/fs2 as follows.
(4.229) ![]()
(4.231) ![]()
where the second equality in (4.228) and (4.230) holds in all points where support curves do not intersect and ![]() and
and ![]() are the bifrequency spectral cross-correlation densities of the Loève bifrequency cross-spectrum (4.190a), (4.190b)
are the bifrequency spectral cross-correlation densities of the Loève bifrequency cross-spectrum (4.190a), (4.190b)
defined analogously to their counterparts (4.20a) and (4.20b) for continuous-time processes.
Solutions of inequalities (4.226) and (4.227) can be easily found in the special case where ![]() and
and ![]() are linear functions with unit slope. Specifically, for a single ACS process xa,i(t) = xa(t), fsi = fs, i = 1, 2, and (*) present, one has
are linear functions with unit slope. Specifically, for a single ACS process xa,i(t) = xa(t), fsi = fs, i = 1, 2, and (*) present, one has ![]() . Thus,
. Thus, ![]() , and (4.226) becomes fs ≥ B + fs/2 + 2B, that is, fs ≥ 6B. This condition, however, can be relaxed to fs ≥ 4B (Section 1.3.9) by exploiting the fact that the support curves are parallel lines (with unit slope) (Gardner et al. 2006), (Izzo and Napolitano 1996) and by using bounds for supports of cyclic spectra.
, and (4.226) becomes fs ≥ B + fs/2 + 2B, that is, fs ≥ 6B. This condition, however, can be relaxed to fs ≥ 4B (Section 1.3.9) by exploiting the fact that the support curves are parallel lines (with unit slope) (Gardner et al. 2006), (Izzo and Napolitano 1996) and by using bounds for supports of cyclic spectra.
As a concluding remark, let us consider GACS processes, which are the other class of processes that, as the class of the SC processes, extends that of the ACS processes. The discrete-time analysis of GACS processes differs from that of SC processes. In fact, in Section 2.5 it is shown that continuous-time GACS processes, unlike WSS, ACS, and SC processes, do not have a discrete-time counterpart and uniformly sampling a continuous-time GACS process leads to a discrete-time ACS process. In addition, in Sections 2.2.2 and 2.2.3 it is shown that a GACS process cannot be strictly band limited and is not harmonizable unless in the special case it reduces to an ACS process (Izzo and Napolitano 2002b; Napolitano 2007a).
4.9.3 Illustrative Examples
In this section, illustrative examples of the results of Section 4.9 are presented. These results which are expressed in terms of Loève bifrequency spectra, can be equivalently formulated in terms of spectral cross-correlation densities (4.20a), (4.20b), (4.232a), and (4.232b) by replacing Dirac with Kronecker deltas.
In the first experiment, a pulse-amplitude-modulated (PAM) signal xa(t) is considered with stationary white modulating sequence, raised cosine pulse with excess bandwidth η, and symbol period Tp. It is second-order cyclostationary with period Tp and strictly band limited with bandwidth (1 + η)/(2Tp). Thus, an upper bound for the bandwidth is B = 1/Tp and the signal has three cycle frequencies αh = h/Tp, h ![]() {0, ± 1} (Gardner et al. 2006). A frequency-warped version of xa(t), namely
{0, ± 1} (Gardner et al. 2006). A frequency-warped version of xa(t), namely
is also considered, with frequency-warping function ψ(f) = Bmtan−1(f/Bs). This kind of frequency warping is used in spectral analysis with nonuniform frequency spacing on the frequency axis (Oppenheim et al. 1971), (Oppenheim and Johnson 1972), (Braccini and Oppenheim 1974). Transformation (4.233) preserves in ya(t) the possible wide-sense stationarity of xa(t) (Franaszek 1967), (Franaszek and Liu 1967), (Liu and Franaszek 1969). In contrast, if xa(t) is ACS, then ya(t) is SC (Section 4.13). Moreover, the signals ya(t) and xa(t) turn out to be jointly SC with Loève bifrequency cross-spectrum having support curves (Section 4.13)
(4.234) ![]()
Computing the bifrequency SCD (4.20a) between ya(t) and xa(t) leads to
where ![]() denote the cyclic spectra of the PAM signal xa(t).
denote the cyclic spectra of the PAM signal xa(t).
In the figures, supports of impulsive functions are drawn as “checkerboard” plots with gray levels representing the magnitude of the density of the impulsive functions. In addition, for notation simplicity, the bifrequency SCD of signals a and b is denoted by ![]() .
.
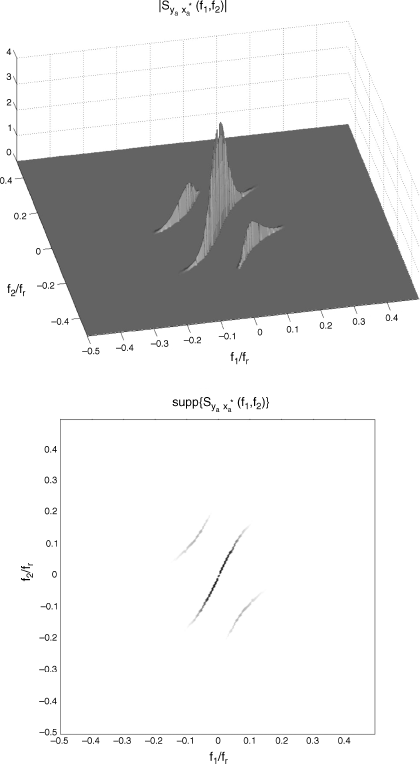
In Figure 4.6, (top) magnitude and (bottom) support of the bifrequency SCD of the continuous-time signal xa(t) are reported as functions of f1/fr and f2/fr, where fr is a fixed reference frequency. In Figure 4.7, (top) magnitude and (bottom) support of the bifrequency SCD in (4.235) of the continuous-time signals ya(t) and xa(t) are reported as functions of f1/fr and f2/fr. In the experiment, η = 0.85, Tp = 4/fr, Bm = 0.21 fr and Bs = 0.1 fr.
Figure 4.6 (Continuous-time) PAM signal xa(t) with raised cosine pulse. (Top) magnitude and (bottom) support of the bifrequency SCD as a function of f1/fr and f2/fr
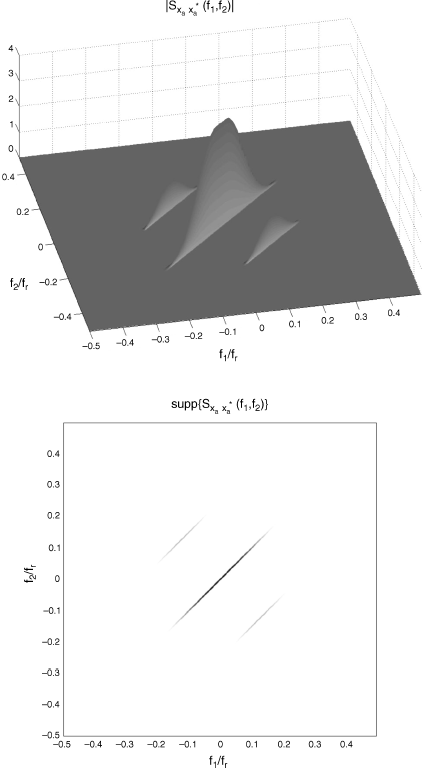
Figure 4.7 (Continuous-time) PAM signal xa(t) with raised cosine pulse and its frequency-warped version ya(t) with frequency-warping function ψ(f) = Bm tan −1(f/Bs). (Top) magnitude and (bottom) support of the bifrequency SCD of ya(t) and xa(t) as a function of f1/fr and f2/fr.
Source: (Napolitano 2011) © IEEE
A unique sampling frequency fs = 1/Ts = fs1 = fs2 is used for both signals. In Figures 4.8 and 4.9, the bifrequency SCD of the discrete-time signals ![]() and
and ![]() , as a function of ν1 and ν2 is reported for two values of the sampling frequency fs. Specifically, in Figure 4.8 (top) magnitude and (bottom) support of the bifrequency SCD for fs = 2B are reported and in Figure 4.9 (top) magnitude and (bottom) support of the bifrequency SCD for fs = 4B are reported. According to the results of Theorem 4.9.20, condition fs = 2B assures non-overlapping replicas (Figure 4.8). However, the SCD of the discrete-time signals along a support curve is not always a scaled version of the SCD of the continuous-time signals along the corresponding support curve ∀ν1
, as a function of ν1 and ν2 is reported for two values of the sampling frequency fs. Specifically, in Figure 4.8 (top) magnitude and (bottom) support of the bifrequency SCD for fs = 2B are reported and in Figure 4.9 (top) magnitude and (bottom) support of the bifrequency SCD for fs = 4B are reported. According to the results of Theorem 4.9.20, condition fs = 2B assures non-overlapping replicas (Figure 4.8). However, the SCD of the discrete-time signals along a support curve is not always a scaled version of the SCD of the continuous-time signals along the corresponding support curve ∀ν1 ![]() [− 1/2, 1/2]. Specifically, in Figure 4.10, the slice of the magnitude of the SCD of the continuous-time signals ya(t) and xa(t) (thin solid line) along
[− 1/2, 1/2]. Specifically, in Figure 4.10, the slice of the magnitude of the SCD of the continuous-time signals ya(t) and xa(t) (thin solid line) along ![]() for αk = 1/Tp and of the rescaled (ν1 = f1/fs) SCD of the discrete-time signals
for αk = 1/Tp and of the rescaled (ν1 = f1/fs) SCD of the discrete-time signals ![]() and
and ![]() (thick dashed line) along ν2 = [Bm tan −1(ν1fs/Bs) − (1/Tp)]/fs ≡ Ψ(k)(ν1), as a function of f1/fr is reported for (top) fs = 2B and (bottom) fs = 4B. In case fs = 2B, the left thick-line replica R1 is exactly overlapped to the thin-line curve but a further aliasing thick-line replica R2 is present. The two replicas correspond to the supports with the same labels R1 and R2 in Figure 4.8 (bottom). In contrast, in case fs = 4B only one thick-line replica (labeled R1 in Figure 4.9 (bottom)) is present which exactly overlaps the thin-line curve. In fact, according to Theorem 4.9.21, condition fs = 4B = fr is sufficient to prevent the presence of aliasing replicas so that (4.228) holds (with fs1 = fs). Specifically, from (4.226) with fs1 = fs2 = fs and B = 1/Tp we have
(thick dashed line) along ν2 = [Bm tan −1(ν1fs/Bs) − (1/Tp)]/fs ≡ Ψ(k)(ν1), as a function of f1/fr is reported for (top) fs = 2B and (bottom) fs = 4B. In case fs = 2B, the left thick-line replica R1 is exactly overlapped to the thin-line curve but a further aliasing thick-line replica R2 is present. The two replicas correspond to the supports with the same labels R1 and R2 in Figure 4.8 (bottom). In contrast, in case fs = 4B only one thick-line replica (labeled R1 in Figure 4.9 (bottom)) is present which exactly overlaps the thin-line curve. In fact, according to Theorem 4.9.21, condition fs = 4B = fr is sufficient to prevent the presence of aliasing replicas so that (4.228) holds (with fs1 = fs). Specifically, from (4.226) with fs1 = fs2 = fs and B = 1/Tp we have
(4.236) 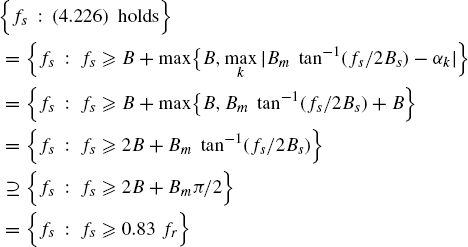
Figure 4.8 (Continuous-time) PAM signal xa(t) with raised cosine pulse and its frequency-warped version ya(t) with frequency-warping function ψ(f) = Bm tan −1(f/Bs). Bifrequency SCD of the discrete-time signals ![]() and
and ![]() , as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 2B.
, as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 2B.
Source: (Napolitano 2011) © IEEE
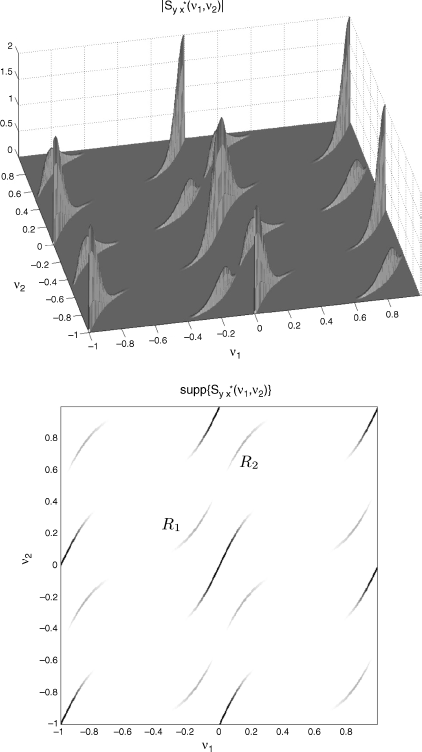
Figure 4.9 (Continuous-time) PAM signal xa(t) with raised cosine pulse and its frequency-warped version ya(t) with frequency-warping function ψ(f) = Bm tan −1(f/Bs). Bifrequency SCD of the discrete-time signals ![]() and
and ![]() , as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 4B.
, as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 4B.
Source: (Napolitano 2011) © IEEE
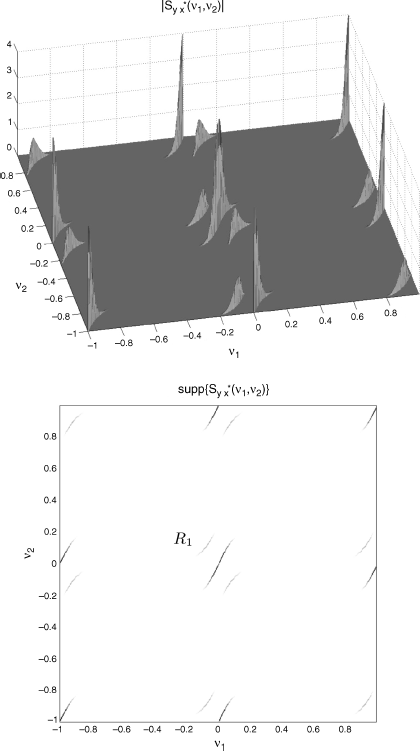
Figure 4.10 (Continuous-time) PAM signal xa(t) with raised cosine pulse and its frequency-warped version ya(t) with frequency-warping function ψ(f) = Bm tan −1(f/Bs). Slice of the magnitude of the SCD of the continuous-time signals ya(t) and xa(t) along ![]() (thin solid line) and of the rescaled (ν1 = f1/fs) SCD of the discrete-time signals
(thin solid line) and of the rescaled (ν1 = f1/fs) SCD of the discrete-time signals ![]() and
and ![]() along ν2 = [ψ(ν1fs) − 1/Tp]/fs ≡ Ψ(k)(ν1) (thick dashed line) as a function of f1/fr. (Top) fs = 2B, (fs/2
along ν2 = [ψ(ν1fs) − 1/Tp]/fs ≡ Ψ(k)(ν1) (thick dashed line) as a function of f1/fr. (Top) fs = 2B, (fs/2 ![]() fr/4), and (bottom) fs = 4B, (fs/2
fr/4), and (bottom) fs = 4B, (fs/2 ![]() fr/2).
fr/2).
Source: (Napolitano 2011) © IEEE

where the last inclusion follows from inequality 0 ≤ tan −1(x) < π/2 for x ≥ 0.
Note that for fs = 2B ![]() fr/2 (Figure 4.10 (top)) the mapping ν1 = f1/fs1 between the arguments of the SCDs of the continuous-and discrete-time signals holds only for f1
fr/2 (Figure 4.10 (top)) the mapping ν1 = f1/fs1 between the arguments of the SCDs of the continuous-and discrete-time signals holds only for f1 ![]() [− fs/2, 0] and ν1
[− fs/2, 0] and ν1 ![]() [− 1/2, 0] whereas for fs = 4B
[− 1/2, 0] whereas for fs = 4B ![]() fr (Figure 4.10 (bottom)) such mapping holds for f1
fr (Figure 4.10 (bottom)) such mapping holds for f1 ![]() [− fs/2, fs/2] and ν1
[− fs/2, fs/2] and ν1 ![]() [− 1/2, 1/2].
[− 1/2, 1/2].
In the second experiment, a PAM signal xa(t) with full-duty-cycle rectangular pulse and baud-rate 1/Tp is considered. Such a signal is second-order cyclostationary with period Tp but is not strictly band limited. It has approximate bandwidth B = 1/Tp and presents cycle frequencies αh = h/Tp, ![]() . When it passes through a multipath Doppler channel, the output signal ya(t) given in (4.56) is SC with Loève bifrequency spectrum given by (4.58) (see also Section 7.7.2). Since the number of cycle frequencies of the continuous-time signal is infinite and the cyclic spectra are not identically zero outside some frequency interval, the discrete-time signal is SC with infinite support curves in the principal spectral domain. However, in the experiment, a finite number Nc of support curves is considered by taking only those curves for which the SCD is significantly different from zero. This number Nc depends on the (finite) number Nr of replicas used to evaluate the aliased bifrequency SCD function. In the experiment, Nr = 5 and Nc = 25 are used and Tp = 4/fr. The multipath Doppler channel is characterized by K = 2, a1 = 1, d1 = 2.5Ts, ν1 = 0.05/Ts, s1 = 0.85, a2 = 0.7, d2 = 6.8Ts, ν2 = − 0.03/Ts, and s2 = 1.25.
. When it passes through a multipath Doppler channel, the output signal ya(t) given in (4.56) is SC with Loève bifrequency spectrum given by (4.58) (see also Section 7.7.2). Since the number of cycle frequencies of the continuous-time signal is infinite and the cyclic spectra are not identically zero outside some frequency interval, the discrete-time signal is SC with infinite support curves in the principal spectral domain. However, in the experiment, a finite number Nc of support curves is considered by taking only those curves for which the SCD is significantly different from zero. This number Nc depends on the (finite) number Nr of replicas used to evaluate the aliased bifrequency SCD function. In the experiment, Nr = 5 and Nc = 25 are used and Tp = 4/fr. The multipath Doppler channel is characterized by K = 2, a1 = 1, d1 = 2.5Ts, ν1 = 0.05/Ts, s1 = 0.85, a2 = 0.7, d2 = 6.8Ts, ν2 = − 0.03/Ts, and s2 = 1.25.
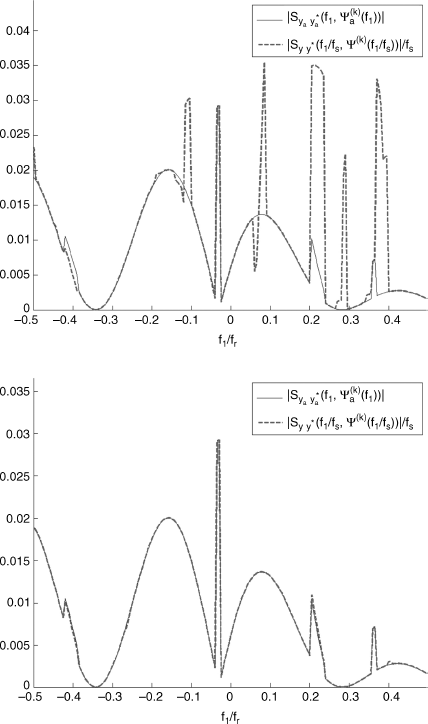
In Figures 4.11 and 4.12, for the continuous-time input signal xa(t) and output signal ya(t), respectively, (top) magnitude and (bottom) support of the bifrequency SCD are reported as functions of f1/fr and f2/fr. In Figures 4.13 and 4.14, (top) magnitude and (bottom) support for fs = 2B and fs = 5B, respectively, of the bifrequency SCD of the discrete-time signal ![]() , as functions of ν1 and ν2 are reported. In Figure 4.15, the slice of the magnitude of the SCD of the continuous-time signal ya(t) along
, as functions of ν1 and ν2 are reported. In Figure 4.15, the slice of the magnitude of the SCD of the continuous-time signal ya(t) along ![]() (thin solid line) and of the rescaled (ν1 = f1/fs) SCD of the discrete-time signal
(thin solid line) and of the rescaled (ν1 = f1/fs) SCD of the discrete-time signal ![]() along ν2 = ν1/s1 − 1/(Tpfs) ≡ Ψ(k)(ν1) (thick dashed line), as functions of f1/fr are reported for (a) fs = 2B
along ν2 = ν1/s1 − 1/(Tpfs) ≡ Ψ(k)(ν1) (thick dashed line), as functions of f1/fr are reported for (a) fs = 2B ![]() 0.685fr and (b) fs = 5B
0.685fr and (b) fs = 5B ![]() 1.71fr. In this experiment, the sufficient condition fs = 2B of Theorem 4.9.20 does not assure a complete non overlap of replicas since the signal xa(t) is not strictly band limited. For fs = 5B replicas turn out to be sufficiently separate and also (4.228) is practically verified.
1.71fr. In this experiment, the sufficient condition fs = 2B of Theorem 4.9.20 does not assure a complete non overlap of replicas since the signal xa(t) is not strictly band limited. For fs = 5B replicas turn out to be sufficiently separate and also (4.228) is practically verified.
Figure 4.11 (Continuous-time) PAM signal xa(t) with rectangular pulse. (Top) magnitude and (bottom) support of the bifrequency SCD as a function of f1/fr and f2/fr
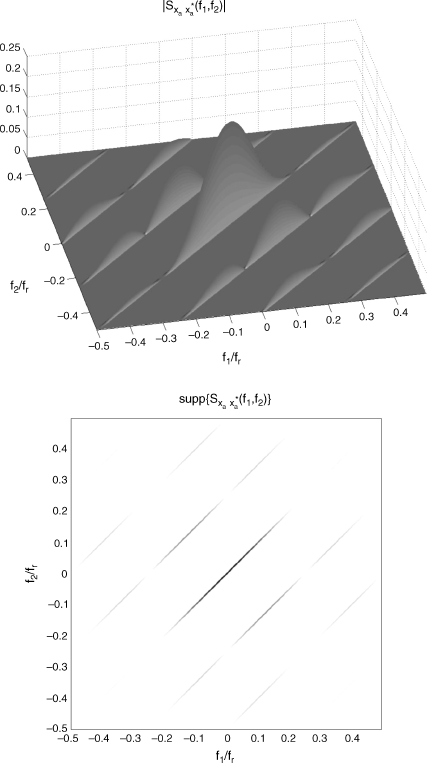
Figure 4.12 Multipath Doppler channel with xa(t) (continuous-time) input PAM signal with rectangular pulse and ya(t) (continuous-time) output signal. (Top) magnitude and (bottom) support of the bifrequency SCD of ya(t), as a function of f1/fr and f2/fr.
Source: (Napolitano 2011) © IEEE
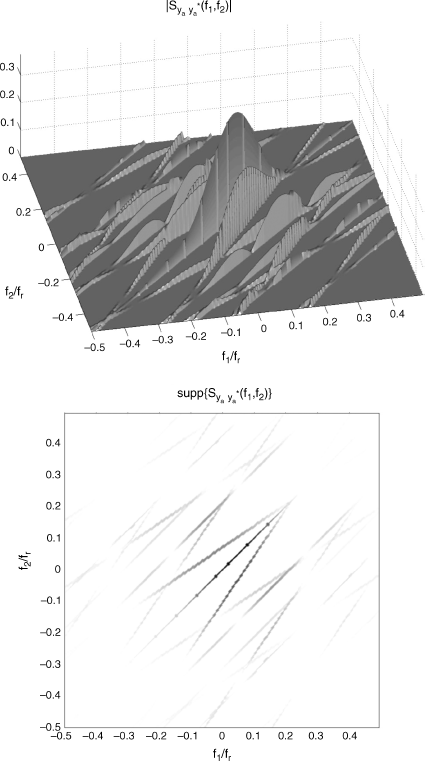
Figure 4.13 Multipath Doppler channel with xa(t) (continuous-time) input PAM signal with rectangular pulse and ya(t) (continuous-time) output signal. Bifrequency SCD of the discrete-time signal ![]() , as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 2B.
, as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 2B.
Source: (Napolitano 2011) © IEEE
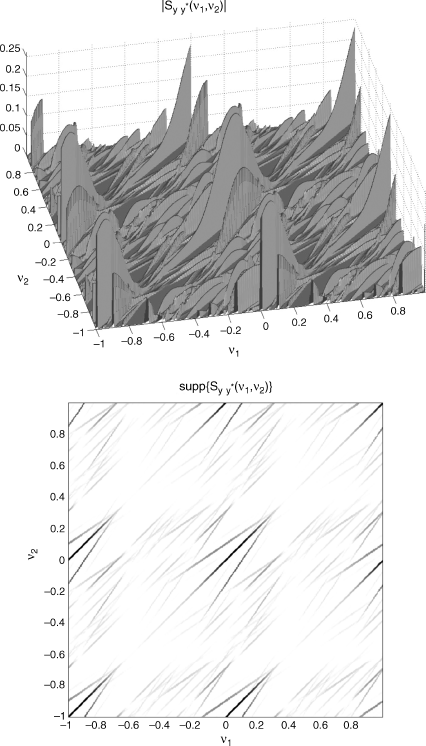
Figure 4.14 Multipath Doppler channel with xa(t) (continuous-time) input PAM signal with rectangular pulse and ya(t) (continuous-time) output signal. Bifrequency SCD of the discrete-time signal ![]() , as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 5B.
, as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 5B.
Source: (Napolitano 2011) © IEEE
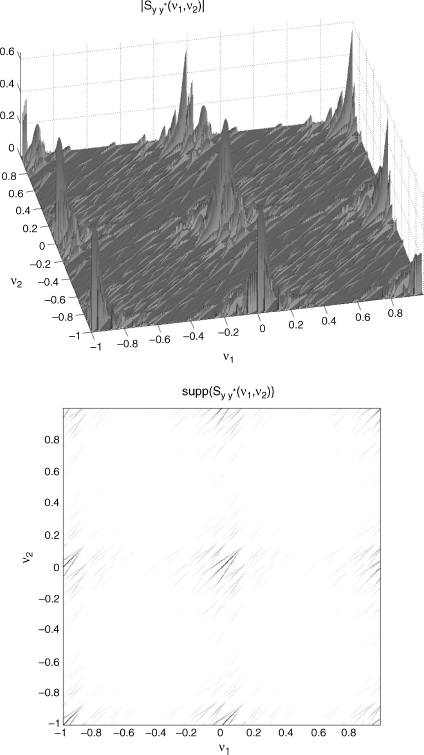
Figure 4.15 Multipath Doppler channel with xa(t) (continuous-time) input PAM signal with rectangular pulse and ya(t) (continuous-time) output signal. Slice of the magnitude of the SCD of the continuous-time signal ya(t) along ![]() (thin solid line) and of the rescaled (ν1 = f1/fs) SCD of the discrete-time signal
(thin solid line) and of the rescaled (ν1 = f1/fs) SCD of the discrete-time signal ![]() along ν2 = ν1/s1 − 1/(Tpfs) ≡ Ψ(k)(ν1) (thick dashed line) as functions of f1/fr. (Top) fs = 2B, (fs/2
along ν2 = ν1/s1 − 1/(Tpfs) ≡ Ψ(k)(ν1) (thick dashed line) as functions of f1/fr. (Top) fs = 2B, (fs/2 ![]() 0.34fr), and (bottom) fs = 5B, (fs/2
0.34fr), and (bottom) fs = 5B, (fs/2 ![]() 0.85fr).
0.85fr).
Source: (Napolitano 2011) © IEEE