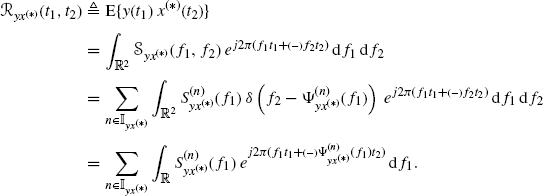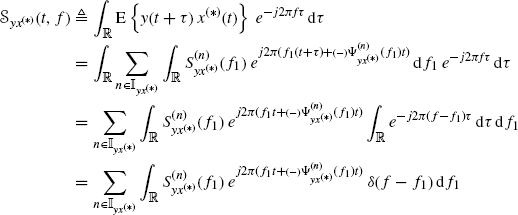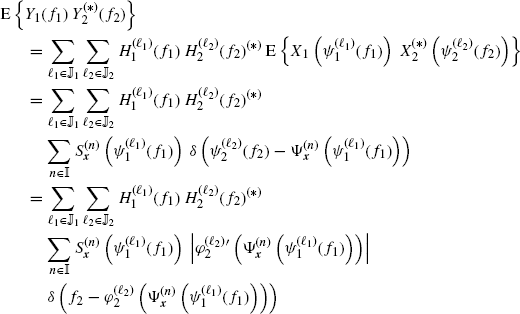5.1 Proofs for Section 4.2 “Characterization of SC Stochastic Processes”

5.1.1 Proof of Theorem 4.2.9 Second-Order Temporal Cross-Moment of Jointly SC Processes

Substituting (4.15) into (4.24b) and using the sampling property of the Dirac delta (Zemanian 1987, Section 1.7) leads to

(5.1)

By using the convolution theorem for the Fourier transform (Champeney 1990, Chapter 6) one obtains (4.24d).

5.1.2 Proof of Theorem 4.2.10 Time-Variant Cross-Spectrum of Jointly SC Processes

Starting from (5.1) with t₁ = t + τ and t₂ = t substituted into, one has

(5.2)

where, in the fourth equality the Fourier transform pair ↔ δ(f − f₁) is used. Equation (4.27b) immediately follows from (5.2) by using the sampling property of Dirac delta (Zemanian 1987, Section 1.7).

5.1.3 Proof of (4.92)

Let ψ(·) be invertible and its inverse ϕ(·) differentiable. It results that (Zemanian 1987, Section 1.7)

(5.3)

Therefore

(5.4)

By using (4.91), (4.89), and (5.4), one has

(5.5)

from which (4.92) follows by using the sampling property of the Dirac delta (Zemanian 1987, Section 1.7).