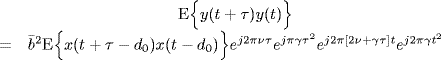7.8 Spectral Analysis of Doppler-Stretched Signals –Constant Relative Radial Acceleration

In the case of constant relative radial acceleration, under the narrow-band conditions (7.246a) and (7.246b), the complex received signal is given by the chirp modulated signal (7.240) (with and replaced by x and y, respectively, for notation simplicity):

(7.346)

Accounting for the Fourier transform pairs

(7.347)

and (Champeney 1990, p. 81)

(7.348)

with a = πγ, we have that the Fourier transform of a delayed, frequency shifted, and chirp modulated signal (7.346) can be expressed as

(7.349)

where O_A[·] denotes the Linear Canonical Transform (LCT) operator (Ozaktas et al. 2001) with parameter matrix

(7.350)

which is coincident with a Fresnel transform with λz = − γ.

In the case of finite-power stochastic processes, the Fourier transform should be intended in the sense of generalized functions (Section 1.1.2), (Gelfand and Vilenkin 1964; Henniger 1970).

7.8.1 Second-Order Statistics (Continuous-Time)

7.8.1.1 Narrow-Band Model

In the case of constant relative radial acceleration, under the narrow-band condition (7.246a) and (7.246b), the complex received signal is given by (7.346). It results that

(7.351)

If (*) is present in (7.351), one obtains the autocorrelation function

(7.352)

If x(t) is ACS, that is, with autocorrelation function

(7.353)

where is a countable set and is the set of cycle frequencies, (7.352) specializes into

(7.354)

Thus, y(t) is GACS and its autocorrelation function can be expressed as

(7.355)

with lag dependent cycle frequencies

(7.356)

and generalized cyclic autocorrelation functions

(7.357)

The functions η_n(τ) are parallel lines with slope γ in the (α, τ) plane. Thus, they do not intersect each other.

If (*) is absent in (7.351), one obtains the conjugate autocorrelation function

(7.358)

If x(t) is ACS, that is, with conjugate autocorrelation function

(7.359)

where is a countable set and is the set of conjugate cycle frequencies, (7.358) specializes into

(7.360)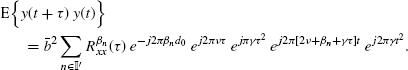

Due to the presence of the term , the conjugate autocorrelation function is not periodic or almost-periodic in t. Therefore, with reference to the conjugate autocorrelation function, the continuous-time signal y(t) is not ACS or GACS. Note that in discrete-time the chirp signal is periodic when and is not AP if .

Accounting for the fact that for b ≠ 0 both integrals

are finite (Champeney 1990, p. 81) one obtains

(7.361)

Thus,

(7.362)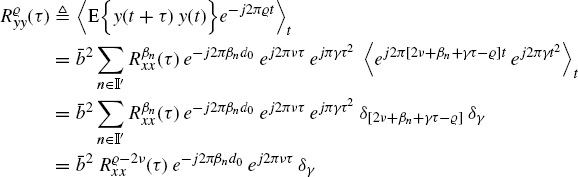

Therefore, the conjugate autocorrelation function can contain a finite-strength additive sinewave component at frequency only if γ = 0 and x(t) has nonzero conjugate cyclic autocorrelation function at conjugate cycle frequency β_n = − 2ν for some β_n A_xx.

Finally, note that the above model for the received signal depends on the length of the observation interval T since it is derived under the narrow-band conditions (7.246a) and (7.246b), that is, and . In order to model the received signal as GACS, however, the further condition |γ|τ_corr > 1/T must be satisfied in order to appreciate the variability of the lag-dependent cycle frequencies with cycle-frequency resolution Δα = 1/T, where τ_corr is the maximum value of |τ| such that is significantly different form zero (Section 2.7.6). For t₀ = 0 conditions (7.246a) and (7.246b) can be written as (7.247a) and (7.247b), respectively, that is and . Therefore, we must have

(7.363)

that is

(7.364)

7.8.1.2 Wide-Band Model

In the case of constant relative radial acceleration the delay is quadratically time varying (see (7.201))

(7.365)

According to (7.236) (with and replaced by x and y, respectively, for notation simplicity) the complex received signal is given by

(7.366)

Thus,

(7.367)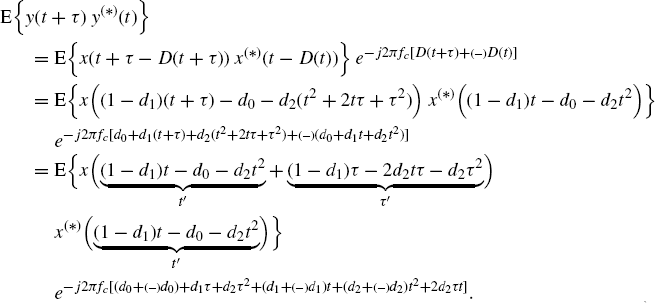

If (*) is present and x(t) is WSS, then the autocorrelation function of y(t) is

(7.368)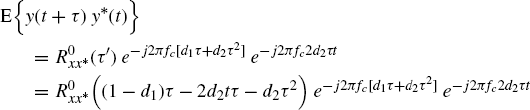

with or . Thus,

(7.369)

This result is due to the presence of t in the argument of or . The infinite time average can be nonzero only if τ = 0. A similar result is obtained if x(t) is ACS.

In (Izzo and Napolitano 2002b, 2005, pp. 200–201), it is shown that cyclic higher-order statistics (moments and cumulants) can have supports contained in lines.

An experiment is conducted to illustrate the behavior of the cyclic autocorrelation function of the output of the Doppler channel existing between transmitter and receiver with constant relative radial acceleration. The transmitted signal x(t) is a binary PAM signal with pulse period T_p = 8T_s and raised cosine pulse with excess bandwidth η = 0.25. The channel introduces a quadratically time-variant delay (see (7.365)) with d₀ = 20T_s, d₁ = − 0.1, and d₂ = − 0.00375/T_s. For an observation interval of 2¹⁰ samples, the narrow-band conditions (7.247a) and (7.247b) are not satisfied. In fact, since B = (1 + η)/(2T_p), we have BT = 80 and |1/d₁| = 10, BT² = 81920T_s and |1/d₂| 266.67T_s.

In Figure 7.18, (top) graph and (bottom) “checkerboard” plot of the magnitude of the cyclic correlogram of the output signal y(t), is reported as a function of αT_s and τ/T_s. Accordingly with (7.369), the cyclic correlogram is significantly different from zero only in a neighborhood of (α, τ) = (0, 0).

Figure 7.18 Output signal of the Doppler channel between transmitter and receiver with constant relative acceleration under the wide-band condition. (Top) graph and (bottom) “checkerboard” plot of the magnitude of the cyclic correlogram as a function of αT_s and τ/T_s.