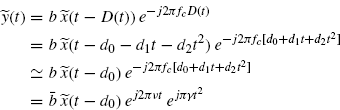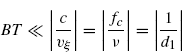7.5 Transmitted Signal: Narrow-Band Condition
Models (7.129) and (7.156) are derived in (Van Trees 1971) for the case of relative motion between transmitter and receiver when the relative radial speed 
can be considered constant within the observation interval (t0, t0 + T). Moreover, in (Van Trees 1971) it is shown that the time–scale factor s can be assumed unity, provided that the condition
is fulfilled, where B is the bandwidth of 
and T the length of the observation interval. Even if condition (7.209) involves both the signal bandwidth and observation interval, it is generally referred to as narrow-band condition.
In the following, the narrow-band condition is derived for a deterministic signal with Fourier transform approaching zero sufficiently fast. The special case of a strictly band-limited signal is considered. Then, the case of a stochastic process with power spectrum approaching zero sufficiently fast is addressed.
Theorem 7.5.1 Narrow-Band Condition –Deterministic Signals. Let x(t) be a differentiable deterministic signal with Fourier transform X(f) such that X(f) = O(|f|−γ) with γ > 2 for |f| > B (that is, |X(f)| ≤ K|f|−γ for |f| > B). It results that
Proof: Let us consider the first-order Taylor series expansion with Lagrange residual term of a delayed version of the signal x(t)
(7.211)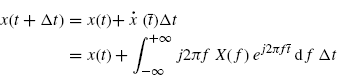 
where 
. One has
(7.212)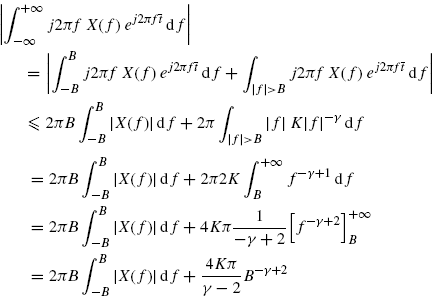 
from which (7.210) follows. Condition γ > 2 assures the existence of all the involved integrals.
In the special case of strictly band-limited signal, the term with the integral on |f| > B is identically zero so that the term O(B−γ+2|Δt|) is absent in (7.210).
From (7.210) it follows that when B|Δt| < 1 (and, hence, a fortiori B−γ+2|Δt| < 1 if B > 1Hz and γ > 2), that is when the time shift |Δt| is much smaller that the reciprocal of the bandwidth B of the signal, then the time shift can be neglected in the argument of x. Similar results can be found in (Swick 1969).
The case of stochastic processes can be addressed by the following result.
Theorem 7.5.2 Narrow-Band Condition –Stochastic Processes. Let x(t) be a finite-power stochastic process with a.e. differentiable time-averaged autocorrelation function 
(Section 1.1.2) and with power spectrum 
such that 
with γ > 2 for |f| > B (that is, 
for |f| > B). For all values of Δt such that 
is differentiable in (0, |Δt|), one obtains
Proof: It results that
where the second equality holds since the time-average does not depend on time shifts of the signal and 
is real and nonnegative.
Let us consider the first-order Taylor series expansion with Lagrange residual term of the time-averaged autocorrelation function around the origin
(7.215) 
where 
denotes the first-order derivative of 
and 
if Δt > 0, 
if Δt < 0. One has
From (7.214) and (7.216), condition (7.213) immediately follows.
Analogously to the case of deterministic signals, in the special case of strictly band-limited stochastic process, the term with the integral on |f| > B is identically zero so that the term O(B−γ+2|Δt|) is absent in (7.213).
7.5.1 Constant Relative Radial Speed
Theorems 7.5.1 and 7.5.2 can be applied in the special case of the linearly time-varying delay introduced by the relative motion between transmitter and receiver with constant relative radial speed. Specifically, from (7.115) (stationary TX, moving RX) and (7.142) (moving TX, stationary RX) we have
(7.217) 
Thus, for t 
(t0, t0 + T) the maximum variation of D(t) is
(7.218) 
Let us assume that
According to Theorems 7.5.1 and 7.5.2, time variations in intervals of width much smaller than 1/B can be neglected. Thus, for t (t0, t0 + T)
(7.220) 
and
(7.221) 
That is, the Doppler channel for the complex signals can be modeled as linear periodically time-variant.
In the case of stationary TX and moving RX, accounting for (7.116), 
and condition (7.219) can be written as
Moreover, in the case of moving TX and stationary RX, accounting for (7.143), 
and condition (7.219) can be written as
which is coincident with (7.209).
Note that when condition (7.219) is satisfied, then s 
1 can be assumed in the argument of 
. Such a condition, however, does not allow to assume s 1 (and, hence, ν 0) in the argument of the complex exponential 
. If condition
holds, then
(7.225) 
Thus, if both conditions (7.219) and (7.224) are satisfied, then
(7.226) 
where 
, and the channel model for the complex signals is LTI.
In the case of stationary TX and moving RX, accounting for (7.131), condition (7.224) can be written as
(7.227) 
that is
In the case of moving TX and stationary RX, accounting for (7.158), condition (7.224) can be written as
(7.229) 
that is
Conditions (7.228) and (7.230) are more stringent then (7.222) and (7.223), respectively, since fc
;B.
7.5.1.1 Example: DSSS Signal
Let us consider a direct-sequence spread-spectrum (DSSS) signal (4.60) used in code-division multiple-access (CDMA) systems with full duty-cycle rectangular chip pulse, chip period Tc, number of chips per bit Nc, and bit period Tb = NcTc. By assuming a bandwidth B 1/Tc for the DSSS signal, one has
(7.231) 
(7.232) 
where rb = 1/Tb = 1/(NcTc) is the bit rate and Nb the number of processed bits.
If 
, c = 3 · 108ms−1, and Nc = 31, then, in the case of stationary TX and moving RX, 1 − s 0.5 · 10−7 and the narrow band condition (7.222) is
(7.233) 
In order to model the channel as LTI, also condition ej2πνt 1 must hold within the observation interval (0, T). Such a condition is generally assumed to be verified when the maximum phase term introduced by the complex exponential within the observation interval is less than Δθ = π/4. If fc = 2 GHz, in case of stationary TX and moving RX, accounting for (7.131) the magnitude of the Doppler shift is
(7.234) 
and, hence, assuming rb = 128 kb s−1 we have
The coherence time τc is the time necessary for a wavefront to cross a λ/2 distance, that is, 
(Sklar 1997, p. 145, eq. (21)). According to such a definition, the channel can be considered stationary within observation intervals less than τc/4. That is, the condition to be fulfilled in order to model the channel as LTI is
which is coincident with (7.235).
7.5.1.2 Example: Sonar Systems
In sonar systems, the narrow band conditions (7.222) or (7.223) involve values of |1 − s| significantly bigger than those for the case of electromagnetic propagation. If the medium is air, then c = 340 ms−1. Therefore, if 
then 1 − s 8 · 10−2. If the medium is water, then c = 1480 ms−1. Thus, if 
then 1 − s 2 · 10−2.
7.5.1.3 Example: Satellite and Space Communications
In the Cassini-Huygens mission, the Cassini probe speed with respect to Huygens in some circumstances is 
(Oberg 2004). Therefore, for c = 3 · 108 ms−1 one has 1 − s 2 · 10−5. In (Oberg 2004), it is shown that, for synchronization purposes, the time-scale factor s cannot be assumed to be unity in the argument of the received complex envelope signal.
Satellites of the Global Position System (GPS) move with a speed 
. The radial speed w.r.t. a stationary observer on the Earth surface is 
where E and ϕ are the elevation angle and the Earth central angle, respectively. For E + ϕ = π/2 − π/16, one has 
.
7.5.2 Constant Relative Radial Acceleration
Let us consider the received signal (7.28) (with A(t) = b not depending on t):
with (see (7.201))
(7.237) 
where 
, 
, d2 = ± aξ/(2c).
The time-varying part of the delay D(t) can be neglected if
Time variations in intervals of width much smaller than 1/B, where B is the bandwidth of 
, can be neglected (Theorems 7.5.1 and 7.5.2). Thus, a sufficient condition to assure (7.238) is
where Δtmax is the maximum delay variation for t (t0, t0 + T). If condition (7.239) is satisfied, from (7.236) it follows that
where,
(7.241a) 
and the second equality in (7.241b) and (7.241c) is obtained for t0 = 0 in the case of stationary TX and moving RX (Section 7.4.1).
Assuming that for t (t0, t0 + T) the function D(t) is monotone, then its maximum variation is
(7.242) 
From (7.200) we have
(7.243)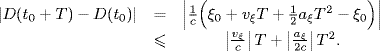 
Therefore, (7.239) is verified if
Since both quantities involved in the left-hand side of (7.244) are positive, a necessary and sufficient condition assuring (7.244) holds is
(7.245)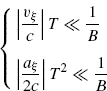 
that is,
Condition (7.246a) is the same as condition (7.222) derived for constant relative radial speed, stationary TX and moving RX. Therefore, (7.246a) and (7.246b) are referred to as narrow-band conditions for the case of constant relative radial acceleration.
In the case of stationary TX an moving RX, |aξ| = |a| and 
. Accounting for (7.241b) and (7.241c), for t0 = 0 conditions (7.246a) and (7.246b) can be written as
7.5.2.1 Example: DSSS Signal
Let us consider a DSSS signal used in CDMA systems, with chip period Tc, number of chips per bit Nc, and bit period Tb = NcTc. It results that B 1/Tc = rbNc and T = NbTb = Nb/rb, where rb = 1/Tb = 1/(NcTc) is the bit rate and Nb the number of processed bits.
The narrow band conditions (7.246a) and (7.246b) specialize into
(7.248a) 
(7.248b) 
respectively.