Developments in Nd:YAG laser welding
Abstract
Laser welding in keyhole (KH) mode using solid-state laser emitting in near infrared at nearly 1 micron wavelength is discussed in this chapter. The main physical processes involved in laser welding are presented and the reasons for using this laser wavelength are shown. Section 3.2 describes the KH geometry and related physical mechanisms controlling its stability. The role of the main operating parameters is also presented. Section 3.3 shows examples of the evolution of keyhole and weld pool behaviour for various welding speeds illustrating the mechanisms discussed in Section 3.2. Finally in the conclusion, expected diagnostics improvements necessary for supporting adapted numerical simulations of this laser welding process are discussed.
3.1 Introduction
The recent advent of the new generation of solid-state lasers based on Nd-YAG, disk or fibre technology, emitting in the near infrared region in the range of 1.03–1.07 micron, has renewed and strongly amplified the interest in using these types of lasers for the welding process. Compared to CO2 lasers, their greater ability to transport this wavelength with a fibre offers an incomparable advantage for industrial applications particularly when anthropomorphic robots are used. Also, these lasers now have a very high level of reliability, with high efficiencies and presently achieve CW powers up to several tens of kW, with an outstanding beam quality reaching quite near diffraction limit. So, for these reasons they have become a very popular tool for joining technology where high performance and high quality with good flexibility are required for the welding of many different materials.
One usually defines two different types of welding. The first one is called the conduction mode: in that case, the absorbed intensity is lower than a given threshold, which depends on the material and the welding speed, where evaporation inside the focal spot is not sufficienthy intense to generate a keyhole. The size of the corresponding melt pool is then mainly controlled by the heat conduction from the focal spot and welding speed. Keyhole (KH) welding or deep penetration welding is the second type of laser welding, which occurs when the laser intensity inside the focal spot is high for generating a high evaporation rate, and so the corresponding recoil pressure depresses the melt pool surface and allows the laser beam to penetrate deeply inside the material. KH generation is therefore the basic mechanism of this mode of welding characterized by a combination of complex physical mechanisms such as laser absorption, conductive and convective heat transfer, a complex hydrodynamic flow around the KH and inside the melt pool, and a strong coupling of the vapour plume with this melt pool.
If conductive welding appears at first glance rather simple to describe, the dominant mechanisms being laser absorption at the melt pool surface, and conductive heat flow inside the melt whose hydrodynamics is controlled by Marangoni surface effect, this is not at all the case with KH welding. One can easily understand that there are many unknowns concerning these very different complex mechanisms that occur during that process and great efforts to understand them are still being undertaken in many laboratories in order to master this important laser process, to make it more reliable and also to improve it in order to achieve better performance. In the first part of this chapter, we will review the main phenomena that are believed to control this process: they concern basically the keyhole (KH) formation and its dynamics, and the resulting hydrodynamics of the melt pool that will define the final weld seam quality. The effect of operating parameters, such as welding speed, laser intensity or power and of course the nature of the material used are also of primary importance for understanding this global behaviour. In the second part, a typical example of evolution of the resulting weld seam is presented when two of the main operating parameters, the welding speed and the incident power, are modified. The chapter concludes by presenting possible directions for improvement of the present understanding necessary for future adaptations to numerical simulations of that process.
3.2 Basics of laser welding in keyhole (KH) mode with solid-state lasers
3.2.1 Main geometrical KH characteristics: wall inclination and KH depth
The basic phenomenon that is at the origin of the KH formation is the recoil pressure that pushes the liquid generated during the surface laser heating, on the sides of the focal spot and allows further penetration of the laser beam inside the material. This ‘piston effect’, which has been described by Semak and Matsunawa (1997) for welding conditions, can be easily understood in the case of pulsed laser welding, or of course during drilling processes that occur at much higher intensities than for welding, i.e. when there is no displacement of material during the laser pulse: the vapour/liquid interface moves into the laser direction, inside the material with a ‘drilling velocity’ Vd and the melt is ejected laterally with a velocity Vm mainly controlled by the recoil pressure Pevap resulting from the strong surface evaporation. When there is a relative displacement between the laser beam and material, defined by the welding speed Vw, the previous scheme is greatly modified: the KH geometry no longer has an axial symmetry: it is then defined by a keyhole front wall (KFW) and a keyhole rear wall (KRW), characterized by their respective inclinations along the welding direction and the side walls can be considered as quite vertical (see Fig. 3.1(a)).
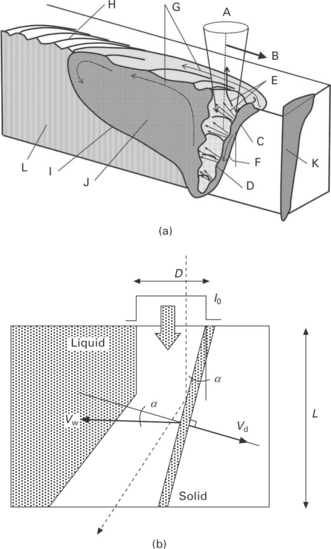
3.1 (a) General skech of laser welding: A: Laser beam; B: Welding speed; C: KH front; D: Humps; E: Vapour jets; F: FKW inclination; G: Melt flow; H: Chevron structure; I: Solidification front; J: Melt pool; K: Weld seam cross section; L: Resolidified material. (b) Scheme of the longitudinal section of a keyhole in a case of full penetration. Incident beam has a uniform intensity I0, with a diameter D. Material is moving from right to left with the welding speed Vw. Under these conditions, the bottom of the KH can be enlarged by the reflected beam.
For this configuration, the main process of laser energy deposition results from the incident laser beam that impinges the KFW under a large angle of incidence. Depending on the partial or full penetration regime of the KH, its aspect ratio L/D (L: KH depth, D: KH diameter), and its KFW inclination α, the local piston effect on the KFW ejects the melt sideways around the KH and downwards along the KFW. This KFW inclination angle α is a very important parameter: first, it defines the main absorptivity A(α) of the incoming laser beam on this surface. As the local angle of incidence is rather high, the absorptivity can be important if one considers the Fresnel equation behaviours and their dependence with the beam polarization (Dausinger and Shen, 1993) that can be modified by local surface roughness (Bergström et al., 2008). Also, macroscopic or microscopic surface deformations resulting from surface instabilities generating humps or ripples (Golubev, 2004) have a non-negligible effect on the level of local absorptivity. Direct measurements of KFW absorptivity by using full penetration welding experiments have shown levels of absorptivity in the range of 60–70% (Fabbro et al., 2005) for non-polarized beams. As a consequence, one should expect that multiple reflections of the laser beam inside the KH are not important for the process of energy distribution inside the KH when medium range incident laser intensities are used.
The second consequence that implies the KFW inclination is that it controls the penetration depth. From geometrical considerations (see Fig. 3.1(b)), it is easy to see that the contribution on the penetration depth L of the impingement of the incident beam with a diameter D, when the entire beam is intercepted, is given by L = D/tgα. Physical analysis of the equilibrium of the KFW has allowed us to determine the main basic parameters of the KH geometry, for stationary conditions (Fabbro, 2010b). One can find that the KFW inclination α is given by a rather simple relation:
In Eq. [3.1], the parameter k is a proportionality factor between the drilling speed Vd and the absorbed intensity: Vd ≈ k · Iabs. This factor k is representative of some energy balance of the process that depends mainly on the workpiece material. It can be determined experimentally for similar conditions of incident laser intensity (typically k ≈ 3 x 10− 11 m3/J for 304 stainless steel) or estimated from the results of the ‘piston model’ of Semak and Matsunawa (1997). So the dependence on penetration depth L with the main operating parameters will be:
where P is the incident laser power. It is interesting to notice that this scaling dependence on the penetration depth L with the ratio P/(D · Vw) has been verified in many experiments (Beyer, 2008; Dausinger et al., 2002; Verhaege and Hilton, 2005), particularly at high welding speeds Vw.
At low welding speeds, because of the small inclination of the KFW, it is easy to show that the resulting absorbed laser intensity on the KFW becomes very low and only depends on the welding speed, with the relation:
Equation [3.3] is interesting because it shows that the absorbed intensity depends only on the welding speed, and not on the incident intensity. This is a very simple self-regulating mechanism: for a given welding speed Vw, as the incident laser intensity I0 increases, the KH depth L also increases (Eq. [3.2]), but the absorbed intensity on FKW is constant, due to the decrease of the FKW inclination (Eq. [3.1]).
Now, let’s consider the KH stability at low welding speed. The KH will be maintained open, if the excess of recoil pressure Pevap over the ambient pressure Pa counterbalances the surface tension pressure Ps = 2σ/D inside the KH (Hirano et al., 2011); as this opening pressure is increasing with the absorbed intensity, Eq. [3.3] shows that for low welding speeds, this excess of recoil pressure should become lower than the characteristic KH closing pressure controlled by surface tension (Fabbro, 2010b). So, for these conditions, the KH cannot be stationary; it closes itself quite periodically, and is continuously re-opened, as in a drilling process, by the continuous incoming incident laser beam. From these considerations, one can estimate that the maximum penetration depth Lmax for achieving a stable KH regime is given by:
where C is a constant defined by the relation between the evaporation pressure Pevap with the absorbed intensity: Pevap − Pa ≈ CIabs, where C is in the order of 1 bar/(MW/cm2) for SUS304 (Fabbro et al., 2006a). For greater penetration depths, one can expect strong fluctuations that may lead to some defects such as trapped porosity from the KH bottom inside the weld seam, strong spatter generation and, as a final consequence, some limitation of the penetration depth. Typically, for SUS304, one can estimate that (Fabbro, 2010b):
The last important effect of the KFW inclination concerns the direction and the level of the dynamic pressure of the vapour emitted by the ablation process on the KFW. We have seen that for the range of incident intensities characteristic of KH generation, the process generates a recoil pressure that can be estimated to be linearly dependent on the absorbed intensity on the KFW. So, as the welding speed increases, the KFW inclination also increases as well as the absorbed intensity on the KFW. Consequently, the recoil pressure also increases and typically can reach a few bars for an absorbed intensity of about 1 MW/cm2 on steel material (Fabbro et al., 2006a). As the direction of expansion of the vapour is perpendicular to the local surface of the KFW, this vapour jet impinges on the KRW with a dynamic pressure Pd that can be similar to the recoil pressure, if the distance between the KFW and KRW is small, which is usually the case. It is the impact pressure Pd of this vapour on the KRW that maintains the KH opened, balancing the sum Ps + Pm of the ‘closing’ pressures of the KRW that result from the surface tension pressure Ps = 2σ/D and from the dynamic pressure Pm ≈ 0.5ρmVm2 due to the liquid melt flowing laterally around the KH with the speed Vm, as a result of the recoil pressure applied on the KFW. (One must mention that if the welding velocity is not too low, the laser beam does not hit the KRW; so we do not have the term Pevap for the previous pressure balance on KRW.)
For these conditions, one can show that the equilibrium of the KRW cannot be stable (Fabbro and Chouf, 2000a, b), and so the KRW shows many fluctuations that are likely to generate some defects inside the melt pool. Moreover, these fluctuations can be even more easily triggered, if one considers that surface instabilities such as humps or ripples are present on the KFW surface, this effect being reinforced at low welding speeds (Golubev, 2004). In that case, important localized evaporation on these humps located on the KFW produces strong jets of vapour that can easily destabilize the KRW. As a result, bubbles of vapour can be generated inside the melt pool. Depending on the fraction content of the trapped shielding gas inside the KH (which may not be negligible, if one considers the very unstable behaviour of the KH in this regime), their position along the KH and the velocity field inside the melt pool, these bubbles can be evacuated at the melt pool surface, or if not, may result as porosity whose final size depends mainly on their shielding gas content when they are initially generated. The dynamic behaviour of these bubbles, whether or not it leads to porosity formation, has been remarkably demonstrated by the various X-ray shadowgraphy experiments realized by the Osaka team (Katayama, 2010) for the last 20 years and also more recently at IFSW in Stuttgart (Abt et al., 2011). Also, some rather recent 2D and 3D numerical simulations have been able to reproduce the complex mechanisms of the interaction of the vapour plume with the melt pool (Amara et al., 2006; Amara and Fabbro, 2008; L. Zhang et al., 2011).
The previous considerations about the KH geometry (and more precisely its KFW inclination defined by the welding speed and the incident laser intensity), and the corresponding direction and dynamic pressure of the emitted vapour allow us to have a general view of the behaviour of the coupling between the KH and the surrounding melt pool:
• At low welding speed, the KH is rather deep, quite vertical and very unstable, leading to irregular collapses. The laser beam impinges on the collapsed liquid wall and pushes it downwards generating bubbles inside the melt pool that are not easily evacuated (with possible pore generation). Upward expansion of the vapour plume induces droplets and spatter generation.
• When the welding speed increases, KFW inclination increases and correspondingly the KH depth decreases. The evaporation on the KFW generates vapour jets that impinge on the KRW, producing different types of defects that may or may not be evacuated, depending on their size and the local induced upward flow of the liquid behind the KRW. So, bubbles leading to pores can be created and also droplets are emitted from the top part of the KRW and/or from the rear rim of the KH aperture. For some range of welding speeds, adapted conditions may lead to quite a stable configuration where the upper part of the KH is opened enough to allow a correct vapour ejection with a quasi-stationary velocity field inside the melt pool. In that case, porosity formation can be suppressed.
• At high welding speed, the KH depth still decreases and becomes rather small. The KFW inclination and therefore the absorbed laser intensity are important, so the resulting vapour jet is intense but it is emitted quite vertically; so, it no longer interacts with the KRW, and the previous defects cannot appear. However, as the melt flow expelled sideways from the KFW has a high velocity under these conditions, the resulting melt pool may present strong undercuts or even humping defects at welding speeds. This evolution of the KH and melt pool behaviour as a function of the welding speed will be detailed in Section 3.3.
3.2.2 Spatter formation
In addition to the porosity formation mechanism, the vapour jet issued from the KFW also plays a very important role in the spatter generation mechanism. From Eq. [3.1], we are able to know the mean direction of the ejected metal vapour, because it is emitted perpendicularly to the KFW whose inclination a increases when the welding speed increases or the incident laser intensity decreases. But when α increases, the vapour jet impinges on the upper part of the KRW, with an increase of its dynamic pressure due to higher absorbed intensity. Therefore, under these conditions, spatters can be generated and are ejected rearwards, in the direction of the vapour jet. By using high-speed video camera, the analysis of the maximum ejection angle of the trajectory of droplets emitted from the rear part of the KH rim confirms the linear relation between the KFW inclination and this maximum angle of droplet trajectory (Weberpals and Dausinger, 2007). In fact, the direction of this spatter emission is deviated from the direction of the vapour jet. This is because the final velocity of the spatters is given by a sum of momentum of the vapour jet emitted perpendicularly from the KFW and an upward directed melt flow occurring on the KRW (Weberpals, 2010). This deviation is more important in partial penetration than in full penetration. This spatter ejection can even be partly controlled and reduced: for similar operating conditions, by inclining the laser axis in the forward direction, the resulting reduction of the KFW inclination makes the vapour jet rather collide with the central part of the KRW, instead of its upper part, which is more sensitive to droplet ejection. In that case, the KH becomes more elongated, and spatter formation or induced defects inside the melt pool are minimized.
There is also another method for reducing spatter emission and for improving the final weld seam quality. It is usually observed that when the laser focal spot is located inside the workpiece, at a distance from the workpiece surface of about 1–3 mm (depending on the corresponding beam waist and beam intensity profile), the weld seam quality is significantly improved and even a greater penetration depth results. This effect is likely to result from the localization of the most intense zone of evaporation in the beam, which corresponds to the minimum focal spot, which is then deep inside the workpiece. At this depth, the KRW and behind it the melt pool, can sustain more easily the impact of the vapour jet, than in the wider upper part of the KRW. So, one can understand that the vapour jet is the main mechanism that can perturb and efficiently modify the hydrodynamics of the melt pool. Its control, if possible, is of primary importance during laser welding. Additional examples will be shown in Section 3.3.
A similar, and even stronger, perturbation is observed when Zn-coated sheets are welded in overlap joint configuration without a gap between the sheets. In that case, hot zinc vapours can only emerge inside the keyhole through a channel that is localized at the sheet interface and emerging at the KFW. Due to their high dynamic pressure (roughly corresponding to the saturation pressure of Zn at steel melting temperature), Zn vapours expel violently the liquid and large amounts of the rear melt pool can be blown away leading to cavities and blowholes in the weld seam. It has been shown experimentally that, depending on the relative position of this sheet interface with the upper surface, this liquid perturbation can be minimized in order to favour the Zn vapour expansion (see Fig. 3.2). The same effect is also obtained when a top-hat intensity distribution is used compared to a ‘peaked’ intensity distribution, because a clear aperture is similarly generated at the bottom of the KRW. Another possible solution consists in using an elongated focal spot along the welding direction that maintains the KRW at enough distance, at about 1 mm, in order to allow the dynamic pressure of Zn vapour to decrease. However, this solution requires a rather large incident laser power (Kielwasser et al., 2000; Fabbro et al., 2006b).
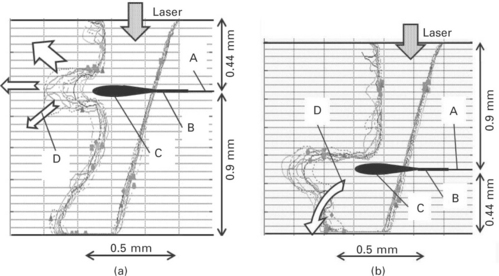
3.2 Computed keyhole profiles when two Zn-coated sheets of different thicknesses are welded in overlap configuration. The RKW is deformed by the Zn vapour jet escaping from a channel at the sheet interface: (a) 0.44 mm/0.90 mm and (b) 0.90 mm/0.44 mm. Experimentally, one observes that case (b) is much more stable than case (a) because the greater enlargement of the KH bottom allows the Zn vapour to escape more easily. A: Sheet interface; B: Zn vapour channel; C: Zn vapour jet; D: Flow followed by the Zn vapours (incident laser power: 4 kW, Vw: 3.5 m/min, top-hat intensity distribution, focal spot diameter: 0.45 mm, 5 ms time interval between each profile for visualizing their fluctuations) (Fabbro et al., 2006b).
It is also well known that an efficient solution to this problem is to maintain a gap of about 0.1–0.2 mm depending on the thickness of the sheet material and the coatings, which allows Zn vapour venting between the two sheets. Some recent simulations of this effect show the resulting modification of the melt flow field (Geiger et al., 2009). For generating such a gap between the two sheets, many techniques have been designed, but an elegant solution was recently proposed by pre-processing dimples on the upper surface of the second sheet before the final assembly (Gu and Shulkin, 2010). These dimples, with controlled height, can be easily generated using a laser weld seam realized in the humping regime, i.e. when the weld seam is obtained at very high welding speed, typically 60–80 m/min. This operation is then very rapidly obtained on these parts, using high-speed remote scanning optics and high beam quality lasers.
At low welding speed, the inclination angle of the KFW is very small, so the keyhole is quite vertical. It is also rather unstable, continuously re-opened and consequently the metal vapour plume is mainly ejected upwards. Under these conditions, this vapour plume has much less impact on the KRW, but interacts mainly by its friction effect along the KH walls. The corresponding shear stress τg and induced upwards melt flow velocity U0 can be estimated using τg ≈ 8ηg Vg/D and U0 ≈ 3 (τg L/ηm ρm)1/3. Typically τg ≈ 100–200 N/m2 and the resulting induced upward melt flow velocity U0 ≈ 5–10 m/s (Fabbro, 2010a). This upwards melt flow is very important and, when it reaches the melt pool surface, it spreads along the radial direction. It is also responsible for the large bumps that are generally observed around the KH rim for these operating conditions. Kelvin-Helmholtz instability can also appear for these high speeds of ejected vapour plume; the previous process is then amplified and may lead to spatter and droplet ejection (Golubev, 1995). It is likely that high beam quality lasers, which generate small focal spot diameters, easily induce these effects. On the other hand, one can also understand the quality improvement generally observed when large keyhole sections such as those obtained with large or elongated focal spots are used (Hohenberger et al., 1999; Luft, 2009). The use of large focal spot diameters is a general rule that can be applied for improving the KH stability.
3.2.3 KH opening stabilization using a side gas jet
We have seen that for low welding speeds, in stationary conditions, the evaporation pressure is not sufficiently intense to maintain an opened keyhole. It is then possible to maintain this opening by using a neutral gas jet delivered inside the keyhole by a small side nozzle (Kamikuki et al., 2002; Fabbro et al., 2006c) (see Fig. 3.3(a)). If the gas is correctly delivered, the dynamical pressure of the gas jet can be adjusted in order to balance the closing pressure controlled by its surface tension effects.
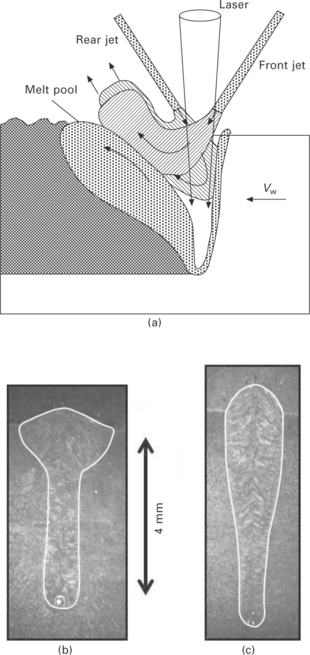
3.3 (a) Scheme of the opening of the KH aperture using a longitudinal side gas jet. The two positions, front or rear, can be used. Weld seam without (b) and with (c) a side gas jet. The weld seam contours have been highlighted (Plaser: 4 kW, Vw: 1 m/min, focal spot diameter: 0.6 mm). A flow rate of 20 l/min of Argon gas was delivered through a 2 mm diameter nozzle. It generates a dynamical pressure of 20 kPa at 5 mm from the nozzle aperture on its axis. By adjusting the argon flow rate, any dynamical pressure can be obtained inside the keyhole in order to avoid its closure.
Figures 3.4 (a) and (b) show characteristic images of the melt pool with and without using the gas jet. The effect of this additional gas flow is very interesting: It maintains the KRW wall at a large distance from the KFW and so the laser beam is no longer intercepted by the KRW fluctuations. Therefore the laser beam can penetrate deeper inside the material. Also, the induced vapour plume is much less important and is more stable compared to conventional welding. Finally the hydrodynamic flow of the melt pool is very different from what is usually observed without the gas jet and it can be controlled: melt flow is ejected rearwards in a continuous, stationary and quite laminar flow. As a result of the use of the side gas jet, a gain of 40–50% in the KH penetration is observed, without any porosity. Also, the wine-cup-shaped weld seam usually observed at these low welding speeds is suppressed (see Fig. 3.3(b, c)) because the flow is no longer directed only upwards but also rearwards by the gas jet. This modified flow also explains the increase of the height of the observed weld seam reinforcement (see Fig. 3.3(c)). 3D modelling of the interaction of a side gas jet with the melt pool was also realized (L. Zhang et al., 2011): it was concluded that an improvement in the stability of the molten pool and a reduction in spatters and pores could be obtained.

3.4 Melt pool behaviour and KH aperture without (a) and with (b) a side gas jet that delivers a dynamical pressure of 8 kPa inside the KH. The resulting elongated KH obtained in that case has a length of about 2 mm. (Welding speed: 3 m/min; Plaser: 3 kW; Spot diameter: 0.6 mm). White vertical arrows show the axis of incident laser beam location.
This technique can be used for severe conditions: using this gas jet-assisted laser welding technique, X. Zhang et al. (2011) have been able to weld 316 L stainless steel plates up to 40 mm thick, in two passes with an 8 kW disk laser and at 0.3 m/min welding speed without any porosity or other defects.
3.2.4 Vapour plume behaviour
Compared to the CO2 laser wavelength, the 1.06 μm of the Nd-Yag laser has a very different behaviour concerning its interaction with the vapour plume. Firstly, as the Inverse Bremsstrahlung absorption coefficient of an ionized gas with a given electronic density follows a λ2 scaling law, one can consider that this absorption mechanism is not at all relevant at 1.06 μm, for incident laser intensities characteristic of welding processes. As a consequence, the temperature of the vapour plume follows the temperature of the surface where the evaporation process occurs; in fact, this plume temperature may be even lower, due to its expansion into the ambient atmosphere and because its reheating cannot occur due to the very low absorption coefficient, as discussed above. So these plume temperatures are rather low, in the range and above the evaporation temperature Tv of the material at atmospheric pressure. Spectroscopic measurements have confirmed this rather low temperature of the vapour plume and correspondingly its very low ionization state (Greses, 2003; Greses et al., 2004; Katayama, 2010). This explains that, unlike CO2 laser welding where the plume temperature in the range of 6,000–10,000 K results from its reheating by the Inverse Bremsstrahlung absorption, the nature of the shielding gas used, such as He, N2 or Ar, has no effect on the final result of welding when 1 μm laser wavelength is used.
The second aspect of the laser–plume interaction concerns the important role of particles ejected back towards the laser along the direction of the beam. These particles have a very wide range of radius r that can vary from a few nanometres when they result from clusters of atoms, aggregates or ultra-fine particles generated by some complex mechanism of local condensation of these metallic atoms, to micron size or above, when they result from liquid droplets detached from the liquid wall by this violent expanding vapour jet as discussed in Section 3.2.2. Because this range of radius particles is typically smaller or about the 1.06 mm wavelength, it is expected that scattering and absorption by these small particles may play a much more important role than with the CO2 10.6 mm laser wavelength. It is known that Mie scattering becomes effective when the ratio r/λ is about one and Rayleigh scattering scales with (r/λ)4, so these mechanisms must be very efficient with short laser wavelengths. The analysis of the relative contribution of the beam absorption (that produces heating of these particles) and of the scattering terms (that induces a significant defocusing effect of the laser beam) shows that absorption is dominant for small particles, while scattering becomes important for larger ones (2πr/λ > 1).
Nevertheless, the application of these theories to experimental conditions is not satisfying due to the lack of precise knowledge of experimental parameters such as the volume ratio (ratio of particle volume to plume volume) or particle radius distribution along the vapour plume. However, Greses et al. (2004) has shown that for welding conditions at 1.06 mm, the particle average size inside the vapour plume varied from 20 to 50 nm when He or Ar shielding gas was used, while for CO2 laser welding, this size was typically 10 times smaller; this likely results from the strong difference of the plume temperature between these two types of welding. Moreover, attenuation and scattering of a probe beam, of different wavelengths, transverse to the vapour plume, confirm the importance of this mechanism occurring at shorter laser wavelengths (Katayama, 2010). In fact, the real importance of the perturbing effect of these scattering mechanisms can really be emphasized when the vapour plume is blown away by an intense transverse gas jet located very near the workpiece surface. Typically, the penetration depth and weld seam area are improved by 15–20% when the vapour plume is correctly ‘cut’. It is likely that the use of a side gas jet, as discussed in Section 3.2.3, also induces such effect by dispersing the vapour plume and therefore reducing its scattering and/or absorbing effect. One must also add that, apart from these localized scattering mechanisms, radial index variation on the shielding gas above the surface induced by thermal heating from the workpiece or from the vapour plume itself, can perturb beam propagation and modify the focal spot intensity distribution, particularly for fibre remote welding (Mitzutani and Katayama, 2009). These results clearly show that the control of the vapour plume and more particularly its size reduction or its suppression by adapted techniques, or of the shielding gas environment, improves the quality and the performance of the welding process. Moreover, due to the large relative variation of the focal spot by these perturbing mechanisms when small focal spots (and/or small apertures of focusing optics) are used, one may expect that these improvements should be very effective when high beam quality lasers are operated.
3.2.5 Welding under vacuum conditions
Welding under vacuum conditions is also another way of reducing the perturbing effects induced by the vapour plume previously discussed. This improvement has already been analysed for high power CO2 laser welding (Poueyo-Verwaerde et al., 1993). At low ambient pressure, the Inverse Bremsstrahlung process of laser absorption by the plasma plume is less efficient due to the decrease of its electronic density as a consequence of the reduction of ambient pressure. Therefore, plume temperature decreases and more laser energy can be transmitted into the KH; typically, on 35NCD16 steel, at a low welding speed of 0.3 m/min and Plaser = 7.5 kW, the KH penetration depth was increased by about 40% when ambient pressure was reduced to about 0.6 kPa. Simultaneously, the characteristic ‘wine cup’ shape of the weld seam top disappeared and large bulging of the melt pool was observed behind the KH.
At 1.06 mm laser welding, if very similar resulting effects are also observed (Abe et al., 2010), the physical mechanisms are rather different. We have seen in Section 3.2.4 that the Inverse Bremsstrahlung absorption process is not effective at this wavelength; therefore the only mechanism that is likely to occur when the ambient pressure is reduced is the strong decrease of the vapour plume density during its expansion outside the KH into this reduced atmosphere. The size of the plume is efficiently reduced due to this 3D expansion just outside the KH aperture and the strong decrease of the observed plume luminosity and its steady behaviour confirm the reduction of perturbing effects. One can also expect that inside the KH, the vapour plume density is also decreased due to this easy and rapid expansion into vacuum. This point also explains the corresponding suppression of spatter emission and the much more stable behaviour of the KH and the melt pool. At low welding speeds, the KH being quite vertical, the vapour plume is then ejected vertically along the KH axis and so perturbs more efficiently laser beam propagation. Improvements observed for welding in vacuum conditions are therefore much more effective at low welding speeds. The consequence of the strong reduction of the absorption and scattering mechanisms in low vacuum conditions, with a more stable KH, is that more laser energy can be injected inside the KH, which then has a greater depth with a narrower size of the weld seam. Abe et al. (2010) obtained an increase of KH depth typically from 20 to 43 mm when the ambient pressure was reduced to about 1 kPa, on 304 stainless steel, at a welding speed of 0.3 m/min (with an incident laser power of 16 kW on a 0.4 mm focal spot diameter). For higher welding speeds, 3–6 m/min, the corresponding increase was only of 15–20%.
One must add that evaporation under vacuum conditions also modifies the temperature threshold for KH generation. As a general condition of KH equilibrium, we have previously seen that it is the excess of the recoil pressure Pevap due to evaporation, over the ambient pressure Pa, which must counterbalance the KH closure pressure Ps due to surface tension, at low welding speeds. Therefore, for vacuum conditions, this condition is realized for a surface temperature of the KH walls with a lower temperature than the usual evaporation temperature Tv. As this reduction of surface temperature can be about 10% of Tv (Hirano et al., 2011), by considering the energy balance of the process, a significantly greater penetration depth has to be expected for similar operating parameters.
3.3 Examples of weld speed variation on global behaviour of keyhole (KH) and melt pool
The previous discussion will be illustrated now by some examples of evolution of the melt dynamics, analysed with a high-speed video camera, for variable welding speeds. Incident laser power and laser spot diameter were kept constant at 4 kW and 0.6 mm, respectively. 304 Stainless steel samples were used, in partial penetration mode. This analysis allows the definition of five main characteristic contiguous regimes, which are only controlled by the welding speed and where the action of the vapour plume on the melt pool is emphasized. This action is controlled by the geometry of the keyhole front, itself defined by the welding speed and incident laser intensity. Although the following observations are done for specific conditions of P = 4 kW and 0.6 mm focal spot diameter, it must be emphasized that these results are general and can be classified as a function of the FKW inclination angle α.
3.3.1 Welding speeds below 5 m/min: ‘Rosenthal’ regime
This regime, occurring for welding speeds lower than 5 m/min, is characterized by a rather large melt pool, even in front of the keyhole, because of the rather low welding speed. The melt pool surface shows many chaotic surface fluctuations and large swellings of liquids fluctuating around the keyhole aperture, which is rather well defined and remains circular (see Fig. 3.5(a)).
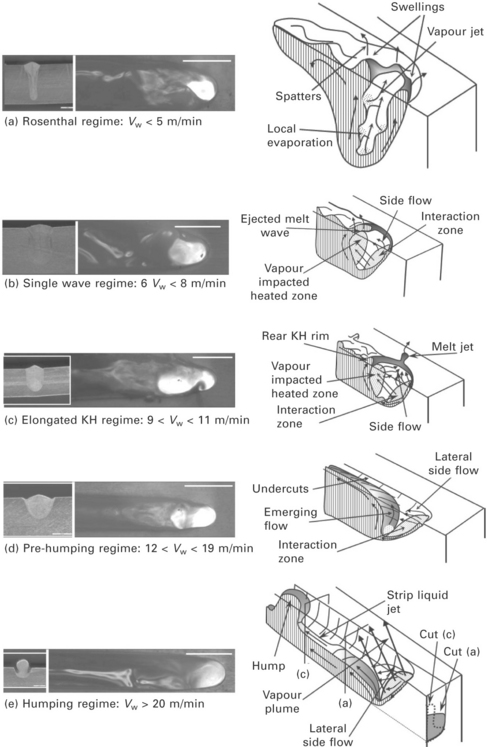
3.5 Characteristic views of KH with surrounding melt pool with corresponding weld seam cross section, and corresponding sketches of the five described regimes obtained for various welding speeds. (Focal spot diameter: 0.6 mm, stainless steel material.) Scale of melt pool: 1 mm.
Because of these fluctuations, there is no clear laminar flow around the keyhole and the Marangoni effect is unlikely to occur for these conditions. Many spatters are emitted mainly from the keyhole rim, and particularly on its front side. On this range of welding speeds, one can see a rapid decrease of the penetration depth as well as large fluctuations of ejection direction of the vapour plume. These fluctuations can be correlated with the previously described melt pool swelling fluctuations. Macrographs of cross sections of the weld seam show a gradual transition of the shape from the well-known ‘wine cup shape’ characteristic of a low welding speed (typically about 1–3 m/min) to a more slender shape for 5 m/min. From the analysis of the keyhole tilting for these low welding speeds, discussed in Section 3.2.1, we know that the keyhole is quite vertical. Therefore, despite these fluctuations, one can schematize this regime by a vertical cylindrical keyhole surrounded by a large melt pool with very limited hydrodynamics. So the description of this situation as a kind of ‘Rosenthal’ heat flow regime, where the keyhole surface is uniformly heated at some temperature close to the evaporation temperature, could be used.
3.3.2 Welding speeds between 6 and 8 m/min: ‘single wave’ regime
This regime is observed for welding speeds ranging from 6 to 8 m/min. It is characterized by the presence of a rather large single swelling generated near the top of the rear keyhole wall (see Fig. 3.5(b)). It is only from this region that large melt droplets are emitted. This large wave is ejected rearwards quite periodically due to back and forth oscillations of the melt pool, leading to quite periodic closures of the keyhole. It is the vapour plume, which is emitted rather deeply inside the keyhole and which collides with the melt pool that triggers these oscillations.
One can observe that only the tilted KFW is clearly heated by the incident laser beam (unlike the ‘Rosenthal’ regime where the luminosity characterizing the laser heated surface was more uniformly and randomly distributed all around the keyhole surface). More interestingly, when the ejected vapour plume collides with the melt pool and lifts it, a corresponding local heating of the liquid surface results from the impact of this energetic heated vapour plume. So the vapour plume not only transfers impulse momentum, but also a non-negligible amount of energy due to its rather high temperature.
It is interesting to note that when high beam quality lasers are used, i.e. with smaller focal spots and correspondingly rather greater penetration depths obtained for this range of rather low welding speeds, one also observes a ‘humping regime’ characterized by very periodic humps generated at the rear of the KH on the weld seam (Behler and Schäfer, 2005; Miyamoto et al., 2004; Thomy et al., 2006). This results from the friction of the ejected vapour acting all along the deep KRW that drags and lifts this part of the melt pool, and whose effect is dominant compared with its colliding effect that occurs when larger focal spots are used.
3.3.3 Welding speeds between 9 and 11 m/min: ‘elongated keyhole’ regime
This regime, which is observed for welding speeds ranging from 9 to 11 m/ min, is characterized by an elongated keyhole whose maximum length of about 2 mm, is obtained at 11 m/min (see Fig. 3.5(c)). This regime also shows some fluctuations, but with much less intense liquid oscillations than in the previous regime, and smaller induced swelling heights. This elongated keyhole shows two characteristic zones that are heated: the first one corresponds, of course, to the more inclined KFW, common to all regimes, and the second one is located at the rear end of this elongated keyhole, inside the melt pool. Moreover, vapour plume seems to be also emitted from the second heated spot and so directed frontward. As in the previous regime, heating by the collision of the vapour plume emitted from the keyhole front is also possible. One could also add that weld seams obtained with this regime have rather good quality, and do not show characteristic defects.
3.3.4 Welding speeds between 12 and 19 m/min: ‘pre-humping’ regime
This regime is observed for welding speeds ranging from 12 to 19 m/min. It is characterized by a rather strong sideward melt flow that contours the KFW, and an important tilting angle. The KH aperture is elongated (but with a shorter length than in the previous regime) and the surface of the following melt pool shows fluctuations characterized by only surface waves with rather small amplitudes. There is also a central melt flow along the KFW that emerges from the bottom of this very stable KFW and is deflected rearwards with its surface melt pool reaching a level close to the initial sample surface (see Fig. 3.5(d)). No more spatters or droplets are emitted, even from the rear rim of the keyhole as in the previous regime. Melt pool surface reaches the level of the surface sample and wets both sides. But above 15–16 m/min welding speeds, undercuts are observed on the sides of the seam. These undercuts begin to be important because the two side flows emitted from the KFW collide with the central emerging flow and press it towards its centre, slightly lifting it. Finally, the vapour plume is very stable; its direction no longer fluctuates and is precisely ejected perpendicularly to the KFW interacting with the top part of the KRW.
3.3.5 Welding speeds above 20 m/min: ‘humping’ regime
For welding speeds above 20 m/min, a very characteristic melt flow appears which corresponds to the humping regime, where the weld seam has very strong undercuts, with solidified large swellings of quite ellipsoidal shape, separated by smaller valleys.
The main central flow always emerges from the bottom of the KFW (see Fig. 3.5(e)); it is strongly deflected rearwards and it rises up to a level that is much lower than the surface sample. So the mean melt velocity inside it is very high. It stays attached to the bottom of the resulting groove along a distance of about 2 mm and then a liquid jet is detached from the central part of this flow and forms a thin vertical strip propagating rearwards at high velocity. The hump appears at a certain distance from the detachment point along this vertical strip of liquid jet (Fabbro et al., 2007). It is the shrinkage of this melt jet strip, due to the Rayleigh instability driven by surface tension, at about 2 mm from the detachment point that generates the instability. This shrinkage cools locally this strip of melt jet and so attaches it to the sample. The fluid flowing inside this strip of melt jet is then stopped at this point, and the hump can grow. The growth of this hump stops when a next shrinkage occurs at about a similar distance from the detachment point that allows the growth of the next hump. Of course, as this thin melt jet strip is located at the centre of section of the groove, very severe undercuts are generated even near the humps. For higher welding speeds, this scheme is not modified.
3.3.6 Analysis of the transition thresholds between these different regimes
The five previous regimes have been observed for a given incident laser power of 4 kW and focal spot of 0.6 mm, for different welding speeds. In fact, one can say that this is a very general result: any set of operating parameters will produce behaviour that corresponds to one of these five regimes. These experiments have been reproduced by using incident laser powers varying between 2.5 and 4 kW and in order to have a greater range of incident intensities, the focal spot was reduced to 0.45 mm. The same regimes were observed but with modified welding speed thresholds. These results are reported in Fig. 3.6 on a laser power-welding speed diagram. Welding is obtained with a KH mode in the region labelled K. Conduction mode is only observed in the region labelled C. Typically, for a welding speed of 25 m/min, KH regime is obtained for incident laser power greater than 0.5 kW. Of course, this power increases with the welding speed.

3.6 Location of different regimes respectively labelled R, S, E, P, H, inside the incident laser power-welding speed plane. Regions corresponding to keyhole (K) and conduction (C) regimes are also indicated. Linear best-fits for the R/S, S/E and E/P transitions have been drawn, with corresponding FKW tilting angle α. (Top-hat intensity distribution; Focal spot diameter: 0.45 mm; Stainless steel material.)
For incident power varying from 2.5 to 4 kW, we have reported the welding speed thresholds between the ‘Rosenthal’/’Single-wave’/’Elongated’/’Pre-humping’/’Humping regimes (these five corresponding regimes are labelled, respectively R, S, E, P, H). Except for the P/H transition, all the other characteristic thresholds increase with the incident laser power. Best-fit lines passing through the origin of these three series of experimental points of these consecutive regimes have also been drawn.
For the P/H transition, it is interesting to note that for incident laser powers smaller than 2.5 kW, no humping instability is observed, even at very high welding speed. Also, when the incident power increases, the threshold for the P/H transition decreases; this behaviour is similar to previous experimental results obtained for different conditions (Thomy et al., 2006). The different behaviour of this P/H transition, compared to the three previous ones, results from the very different mechanisms driving this humping instability. It is also interesting to notice that if we extrapolate the P/H transition to higher incident powers, the pre-humping regime should disappear.
From our previous analysis of the keyhole front equilibrium, one can relate the slope of the three best-fit lines plotted in Fig. 3.6 through the experimental thresholds of the corresponding transitions, with the mean inclination of the KFW. The combination of Eqs [3.1] and [3.2] gives a linear relation between incident laser power P and welding speed Vw:
where the slope B of this linear relation between P and Vw, is given by:
Using Eq. [3.7], the KFW inclination angles α that would reproduce the slopes of these three best-fit lines in Fig. 3.6 are 15°, 30° and 45° for respectively the R/S, S/E and E/P transitions. In fact, these angles are in fair agreement with the corresponding experimental measurements obtained by using the high speed videos.
This model shows that this slope B is proportional to the penetration depth L (Eq. [3.7]). So, for a given transition (R/S, S/E or E/P), all the welding speed thresholds corresponding to that transition will occur at the same penetration depth or KFW inclination. Of course, as expected, when one goes from R to P regimes, the corresponding penetration depths decrease as the welding speeds increase.
So these results indicate that the transition between the first four regimes is basically controlled by a characteristic tilting angle of the KFW. As we have seen that this angle also defines the direction and the dynamic pressure of the emitted vapour plume (this vapour plume being directed perpendicularly to its emitting surface), these results clearly confirm that it is the level of interaction of the vapour plume with the rear melt pool that defines the type of hydrodynamic regime. At low welding speeds, the KFW is slightly tilted; the absorbed intensity is then rather small, as well as the dynamic pressure of vapour. The vapour plume is directed quite horizontally inside the melt pool and so perturbs the melt pool from its bottom. This would correspond to the occurrence of the single wave regime. As the welding speed increases, the tilting angle increases, as well as the absorbed intensity and correspondingly the dynamic pressure of the vapour plume. But this vapour plume is more emitted quite vertically and therefore perturbs more efficiently the top part of the melt pool as in the pre-humping regime.
3.4 Conclusion and future trends
We have described in this chapter the main physical mechanisms that control the quality of the process of laser welding in KH mode. The main conclusion that results is the very important role played by vapour plume generated by the evaporation process that leads to the KH formation. As important is the direction of this vapour plume defined by the KFW inclination. In fact, two main operating parameters, the incident laser intensity and the welding speed, control both this direction and the dynamic pressure of the vapour plume. We have seen that this vapour plume can perturb the welding process in two ways: first by perturbing the beam propagation, by scattering and/or absorbing the incident incoming beam, particularly when small focal spots or low aperture optics are used. As a general rule, it is recommended to blow away the vapour jet each time it is possible, in order to get reproducible, constant and non-perturbed conditions of irradiations. The vapour jet can also strongly perturb the melt pool geometry and its hydrodynamics by its impact on the KRW. The final quality of the weld seam is a sensitive function of the method used to attenuate these perturbations. We have seen that enlarging the focal spot, for example by using a side gas jet that repels the KRW to larger distances from the KFW, or finding an adapted defocused position, or inclining the incident laser beam, or even welding in vacuum conditions may be possible solutions that should improve the final quality, but of course their possible use must be balanced with the induced constraints.
However, there are still many unknowns related to different mechanisms and future experiments should be focused on them. One can mention several points that should be improved in the near future. A precise knowledge of absorption mechanisms on the KFW is necessary. This could be helped by determining the KFW surface geometry by adapted experiments with high time and space resolution, improving, for example, present high-speed video imaging and/or X-ray shadowgraphy techniques. This problem of surface instabilities generated by non-linear coupling of thermal field and hydrodynamic response should also be more deeply analysed on a theoretical basis. The knowledge of resulting recoil pressure is also rather poor; as we have seen, this parameter is very important because it controls melt side-flow velocity and dynamic pressure of the vapour jet. Presently, very few experiments have been done to determine this recoil pressure for this range of absorbed intensity. Moreover, the effect of several parameters such as the ambient pressure and the nature of alloying elements of the workpiece make the determination of recoil pressure rather complex. Also, the thermodynamic state of metal vapour (mean density, temperature, cluster or particles distribution, flow field, etc.) is completely unknown at present. We have seen that this point is very important for the beam propagation into the vapour plume outside the KH; but for inside the KH, beam scattering should control its propagation and so the resulting beam homogenization should interfere with the previous surface instabilities and absorption mechanisms.
Concerning the melt pool, its geometry, and particularly the shape of its KRW, and also its dynamics flow field, should be analysed with greater spatial and temporal precision than presently. High-speed X-ray shadowgraphy, possibly using tracers, will be an indispensable tool. One should also add that a better knowledge of the surface tension or the dynamic viscosity of the workpiece material dependence with temperature would be useful. Finally, one could also remark that there is an important thermodynamic parameter, which is the temperature, which is usually poorly measured during experiments and which is always a direct output of numerical simulations. Having diagnostics able to give time and space resolved temperature distribution in a sub-melting to evaporation temperature range is still a challenge.
So, the precise determination of all these very different parameters should be important data that must be compared with corresponding results of numerical simulations. It is interesting to note that already, several publications begin to show the possibility to realize 3D numerical simulations of laser welding where these main various mechanisms can be described self-consistently, for non-stationary conditions, and where the hydrodynamics of the melt pool and vapour/free surface interaction are also taken into account (Ki et al., 2002a, b; Dasgupta et al., 2007; Otto et al., 2011; L. Zhang et al., 2011; Pang et al., 2011). Depending on their initial various hypotheses and also computational facility used, the main phenomena involved in the coupling between the KH and the melt pool dynamics discussed in that chapter, have already been correctly reproduced (Pang et al., 2011). So, the numerical results of simulations are presently very encouraging. We are convinced that with continuous efforts on improvements to these numerical simulations on one hand, and, on the other, with the corresponding experimental progress on several experimental diagnostics as mentioned previously, one should be able to have, within a few years, very powerful simulation tools that are able not only to reproduce precisely the main observed characteristics, but also to optimize operating parameter selection for a targeted goal, by avoiding long series of experiments.
3.5 References
Abe, Y., Mizutani, M., Kawahito, Y., Katayama, S. ‘Deep penetration welding with high power laser under vacuum’, Proceedings of the ICALEO 2010 Conference. CA: Anaheim; 2010. [648–653].
Abt, F., Boley, M., Weber, R., Grag, T., Popko, G., Nau, S. Novel X-ray diagnostic for in-situ diagnostics of laser based processes – first approach. Physics Procedia. 2011; 12:761–770.
Amara, E. H., Fabbro, R. Modelling of gas jet effect on melt pool movements during deep penetration laser welding. J. Phys. D: Appl. Phys.. 2008; 41:055503.
Amara, E. H., Fabbro, R., Hamadi, F. Modelling of the melted bath movement induced by the vapour flow in deep penetration laser welding. J. Laser Appl.. 2006; 18:2–11.
Behler, K., Schäfer, P. Miami, FL, Oct. 31–Nov. 3. Melt pool dynamics in high speed welding with modern high power solid state lasers. Proceedings of the ICALEO 2005 Conference. 2005:1026–1031.
Bergström, D., Powell, J., Kaplan, A. The absorption of light by rough metal surfaces – a three-dimensional ray-tracing analysis. J. Appl. Phys.. 2008; 103(10):103515.
Beyer, E. ‘High power laser materials processing – new developments and trends’, Proceedings of the 3rd PICALO 2008 Conference. China: Beijing; 2008. [5–9].
Dasgupta, A. K., Mazumder, J., Li, P. Physics of zinc vaporization and plasma absorption during CO2 laser welding. J. Appl. Phys.. 2007; 102:053108.
Dausinger, F., Shen, J. Energy coupling efficiency in laser surface treatment. ISIJ International. 1993; 33:925–933.
Dausinger, F., Berger, P., Hügel, H. ‘Laser welding of aluminium alloys: problems, approaches for improvement and applications’, Proceedings of the ICALEO 2002 Conference, Scottsdale, AZ. Oct.. 14–17, 2002.
Fabbro, R. in Advances in Laser Material ProcessingLawrence J., Pou J., Low D., Toyserkani E., eds. Physical mechanisms controlling keyhole and melt pool dynamics during laser welding. Woodhead Publishing: Cambridge, 2010:211–241.
Fabbro, R. Melt pool and keyhole behaviour analysis for deep penetration laser welding. J. Phys. D: Appl. Phys.. 2010; 43:445501.
Fabbro, R., Chouf, K. Dynamical description of the keyhole in deep penetration laser welding. J. Laser Appl.. 2000; 12:142–148.
Fabbro, R., Chouf, K. Keyhole modelling during laser welding. J. of Appl. Phys.. 2000; 87:4075–4083.
Fabbro, R., Slimani, S., Coste, F., Briand, F. Study of keyhole behavior for full penetration Nd-Yag CW laser welding. J. Phys. D. : Appl. Phys.. 2005; 38:1–7.
Fabbro, R., Slimani, S., Coste, F., Briand, F., Dlubak, B., Loisel, G. Scottsdale, AZ, Oct. 30-Nov. 2. Analysis of basic processes inside the keyhole during deep penetration Nd-Yag CW laser. Proceedings of the ICALEO 2006 Conference. 2006:1–79.
Fabbro, R., Coste, F., Goebels, D., Kielwasser, M. Study of CW Nd-Yag laser welding of Zn-coated steel sheets. J. Phys. D. : Appl. Phys.. 2006; 39:401–409.
Fabbro, R., Slimani, S., Doudet, I., Coste, F., Briand, F. Experimental study of the dynamical coupling between the induced vapour plume and the melt pool for Nd-Yag laser welding. J. Phys. D. : Appl. Phys.. 2006; 39:394–400.
Fabbro, R., Slimani, S., Coste, F., Briand, F. Munich, Germany, June. Experimental study of the humping process during Nd:Yag CW laser welding. Proceedings of the LIM Conf. 2007:18–21.
Geiger, M., Leitz, K. H., Koch, H., Otto, A. A 3D transient model of keyhole and melt pool dynamics in laser beam welding applied to the joining of zinc coated sheets. Prod. Eng. Res. Devel.. 2009; 3:127–136.
Golubev, V. S. ‘On possible models of hydrodynamical nonstationary phenomena in the processes of laser beam deep penetration into materials’, Proc. SPIE. 1995; 2713:219–230.
Golubev, V. S. Melt removal mechanisms in gas-assisted laser cutting of materials, 2004. [Eprint No. 3. Shatura: ILIT RAS].
Greses, J. Plasma/plume effects in CO2 and Nd:Yag laser welding. Dissertation: University of Cambridge, Cambridge; 2003.
Greses, J., Hilton, P. A., Barlow, C. Y., Steen, W. M. ‘Plume attenuation under high power Nd:Yttritium-Aluminum-Garnet laser welding’, J. Laser Applications. 2004; 16(1):9–15.
Gu, H., Shulkin, B. ‘Remote laser welding of Zn-coated sheet metal component in a lap configuration utilizing humping effect’, Proceedings of the ICALEO 2010 Conference. CA: Anaheim; 2010. [380–385].
Hirano, K., Fabbro, R., Muller, M. Experimental determination of temperature threshold for melt surface deformation during laser interaction on iron at atmospheric pressure. J. Phys. D: Appl. Phys.. 2011; 44:435402.
Hohenberger, B., Chang, C., Schinzel, C., Dausinger, F., Hügel, H. ‘Laser welding with Nd:Yag multi-beam technique’, Proceedings the ICALEO 1999 Conference. San Diego, CA. 1999; 87:D167–D176.
Kamikuki, K., Inoue, T., Yasuda, K., Muro, M., Nakabayashi, T., Matsunawa, A. ‘Prevention of welding defect by side gas flow and its monitoring method in continuous wave ND:Yag laser welding’, J. Laser Applications. 2002; 14:136–145.
Katayama, S. in Advances in Laser Material ProcessingLawrence J., Pou J., Low D., Toyserkani E., eds. Understanding and improving process control in pulsed and continuous wave laser welding. Woodhead Publishing: Cambridge, 2010:181–210.
Ki, H., Mohanty, P. S., Mazumder, J. Modelling of laser keyhole welding: Part I Mathematical modeling, numerical methodology, role of recoil pressure, multiple reflections and free surface evolution. Metall. Mater. Trans.. 2002; A33:1817–1830.
Ki, H., Mohanty, P. S., Mazumder, J. Modelling of laser keyhole welding: Part Simulation of keyhole evolution, velocity, temperature profile, and experimental verification. Metall. Mater. Trans.. 2002; A33:1831–1842.
Kielwasser, M., Fabbro, R., Petring, D., Poprawe, R. ‘Physical processes during pulsed Nd:YAG laser and CO2 laser welding of zinc coated steel’, in Laser Application to Auto Industry – Proceedings of ICALEO 2000 Conference. Detroit, MI. 2000; 89:A10–A19.
Luft, A. ‘New applications for welding with diode lasers’, Proceedings of the 5th International WLT-Conference on Lasers in Manufacturing. June: Munich; 2009.
Mitzutani, M., Katayama, S. ‘Numerical calculation of laser beam path influenced by high temperature gas above specimen during laser welding’, Proceedings of ICALEO 2009 Conference. FL: Orlando; 2009. [600–609].
Miyamoto, I., Park, S. J., Ooie, T. Erlangen, Germany. High-speed microwelding by single-mode fiber laser. Proceedings of the 4th LANE 2004 Conf. 2004:55–66.
Otto, A., Koch, H., Leitz, K. H., Schmidt, M. Numerical simulations – a versatile approach for better understanding dynamics in laser material processing. Physics Procedia. 2011; 12:11–20.
Pang, S., Chen, C., Zhou, J., Yin, Y., Chen, T. A three-dimensional sharp interface model for self-consistent keyhole and weld pool dynamics in deep penetration laser welding. J. Phys. D: Appl. Phys.. 2011; 44:025301.
Poueyo-Verwaerde, A., Fabbro, R., Deshors, G., De Frutos, A. M., Orza, J. M. Experimental study of laser induced plasmas in welding conditions with CW CO2 laser. J. Appl. Phys.. 1993; 74:5773.
Semak, V., Matsunawa, A. The role of recoil pressure in energy balance during laser materials processing. J. Phys. D: Appl. Phys.. 1997; 30:2541–2552.
Thomy, C., Seefeld, T., Wagner, F., Vollertsen, F. Scottsdale, AZ, Oct. 30-Nov. 2. Humping in welding with single mode fiber lasers. Proceedings of the ICALEO 2006 Conference. 2006:543–552.
Verhaeghe, G., Hilton, P. ‘The effect of spot size and beam quality on welding performance when using high-power continuous wave solid-state lasers’, Proceedings of the ICALEO 2005 Conference. FL: Miami; 2005. [264–271].
Weberpals, J. Nutzen und Grenzen gutter Fokussierbarkeit beim Laserscheweinssen. Dissertation: University of Stuttgart, Herbert Utz Verlag GmbH; 2010.
Weberpals, J., Dausinger, F. ‘Influence of inclination angle on spatter behaviour at welding with lasers of strong focusability’, Proceedings of the ICALEO 2007 Conference. FL: Orlando; 2007. [858–865].
Zhang, L., Zhang, J., Zhang, G., Bo, W., Gong, S. An investigation on the effects of side assisting gas flow and metallic vapour jet on the stability of keyhole and molten pool during laser full-penetration welding. J. Phys. D. : Appl. Phys. 2011; 44:135201.
Zhang, X., Ashida, E., Tarasawa, S., Anma, Y., Okada, M., Katayama, S., Mizutani, M. ‘Welding of thick stainless steel plates up to 50 mm with high brightness lasers’, J. Laser Applications. 2011; 23(2):9–15.
3.6 Appendix: list of symbols
| A(α) | angular dependence of absorptivity |
| A0 | absorptivity under normal incidence |
| B | slope of relation between laser power and welding speed (J/m) |
| C | slope of relation between evaporation pressure and absorbed intensity (s/m) |
| D | spot diameter (m) |
| Iabs | absorbed laser intensity (W/m2) |
| Icond | conduction loss inside solid (W/m2) |
| I0 | incident laser intensity (W/m2) |
| k | constant (m3J- 1) |
| L | keyhole depth (m) |
| Lmax | maximum depth of a quite stable keyhole (m) |
| P | incident laser power (W) |
| Pa | ambient atmospheric pressure (N/m2) |
| Pd | dynamic pressure of ejected vapour plume (N/m2) |
| Pevap | evaporation pressure (N/m2) |
| Ps | keyhole closing pressure due to surface tension (N/m2) |
| r | particle radius inside the vapour plume (m) |
| Tv | workpiece evaporation temperature (K) |
| Vd | drilling velocity (m/s) |
| Vg | vapour plume velocity (m/s) |
| Vm | melt velocity (m/s) |
| Vw | welding speed (m/s) |
| α | inclination of the front keyhole wall (rd) |
| λ | laser wavelength (m) |
| ρm | melt density (kg/m3) |
| σ | surface tension of metal liquid (N/m) |
| τg | shear stress (N/m2) |
| ηg, ηm | dynamic viscosity of metal vapour and melt (Pa.s) |
