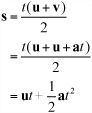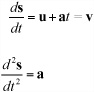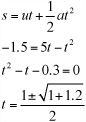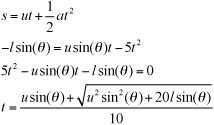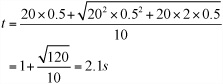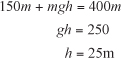Velocity is the rate of change of a particle’s position. Acceleration is the rate of change of velocity. Like velocity, acceleration is a vector. Its components are measured in units of velocity divided by units of time. If your units of distance are meters and your units of time are seconds, how things are measured is then set. Distance and displacement are measured in meters (m). Speed and velocity are measured in meters per second (ms^-1). Acceleration is measured in meters per second per second, or meters per second squared (ms^-2).

Because acceleration is a vector, it can be measured in any direction. If a particle is moving in a straight line and its speed is decreasing at a constant rate, the particle is experiencing a constant acceleration in the direction opposite to its motion. This is somewhat different from the common usage of the word “accelerate,” which refers only to increasing speed. When the speed of a car is decreasing, for example, you usually say that it is decelerating. You might say that its deceleration is the negative of its acceleration. However, this doesn’t really tell you a great deal, and in physics, the term deceleration is not usually used.

With a and u representing vectors, if a particle’s acceleration a is constant, for each unit of time, the velocity changes by a. If the particle starts with a velocity u, then after time t, its velocity v will equal u + at. What will its position be at that time?

You can calculate the position quite simply. Take the mean velocity over the time period t. If at time t the velocity is v, then the mean velocity is (u + v)/2, and the displacement s is t(u + v)/2. Substituting the previous value for v you get

If you look back at Chapter 6, you can see that this result makes perfect sense. If you differentiate with respect to time, you get

This fits your definitions of velocity and acceleration. Velocity is the rate of change of displacement, and acceleration is the rate of change of velocity. Notice also that if acceleration is zero, the formulas reduce to a simple version for motion with a constant speed, s = ut.

You now have three formulas relating the values s, u, v, a and t. Each formula relates four of the five quantities. By artful substitution you can derive still more equations. A fourth equation relates v, u, a and s. A fifth relates v, a, s and t. In the end you have a complete set of formulas for the five quantities:

Since there is no simple way to multiply vectors together, the fifth formula doesn’t make very much sense in terms of vectors; it is presented in terms of scalars, and it assumes that the vectors s, a, v, and u are all collinear. It is really just a restatement of the previous formulas. As you can see, Equation 3 and Equation 4 can be derived from Equation 1 and Equation 2.

Using these formulas, you can calculate any one of the parameters in terms of any three of the others. Say that you know the current velocity and acceleration of a particle and how long it has been moving. You can calculate both its relative initial position and its initial velocity:

It’s unlikely you will need to do this particular calculation often. Since you usually know u, a and t, it is the velocity or position that you need to find. The formulas allow you to find this directly.

As a general approach to getting the position, the calculatePositon() function takes four arguments and returns the position:

function calculatePosition(initialPosition,
                           initialVelocity,
                             acceleration, time)
   return initialPosition + initialVelocity * time
                          + acceleration * time * time/2
end function

The story goes that Galileo wondered if a heavy ball and a light ball would fall at different speeds. He climbed to the top of the leaning Tower of Pisa bearing a heavy ball and a light ball, dropped the two balls off the top, and watched. They fell at the same speed. By this experiment, he proved that the speed at which an object falls is independent of its weight. As it stands, however, he never performed such an experiment. Instead, he stayed in his studio and arrived at his law by pure logic. It is worth looking at his proof because it’s very ingenious.

Suppose you have two objects, A and B, where A is heavier than B. Now suppose that it is true that heavier objects fall faster than light ones. If you tie A to B and drop them from a height, B will fall more slowly, so it will act as a drag on A, like a parachute. This would mean that if A and B were tied together, they would fall more slowly than A. But this makes no sense, because A and B tied together are heavier than A, which should fall faster than A. So something is wrong, and it must be the original hypothesis.

But how exactly does a ball fall through the air? What does gravity do? This is a complicated question, one that is fundamental to science and to which science does not yet have a final answer. For now, you can give a simple answer. As long as the ball doesn’t significantly change height, while it is flying it experiences a constant downward acceleration. The acceleration is due to gravity, g. Ignoring the effects of air resistance, this is the only way that the speed and direction of the ball change. At sea level on earth, |g| is approximately 9.8 m/s². However, to simplify calculations, you’ll use the value of 10 in this chapter.

Using this beginning, you can make some simple calculations straight away. For example, consider a question. If you throw a ball straight upward with a speed of 5 ms^-1, how high will it go? There is a small trick here. When the ball reaches the top of its motion, its speed is zero. This means you can use your equation of motion:

It’s worth looking at exactly what you did here. The values s, u, v, and a are all vector quantities, but in this calculation you have treated them as plain numbers. Your only concession to their vector nature is that you used the negative value –10 for g. This is done because it is in the opposite direction from the other quantities. This is possible because the whole of the motion takes place in a single vertical line, a one-dimensional space. The vectors have just one component, a single-directed number.

In case this seems to be stressing the point too much, think about another question. How fast will the ball be traveling when you catch it again? This time, you are looking for a value of v such that s = 0. You can use the same formula as before:

Solving, you arrive at

Of course, when v = 5, this is the beginning of the motion, and by definition, s = 0. At the end of the motion, v = –5, which is to say that the speed at which the ball lands is the same as it was when it was thrown, but the direction of motion has been reversed. Understanding the directed nature of the quantities you are measuring is essential to using the formulas correctly.

To see how useful these equations are, ask one last question. If the ball leaves your hand 1.5 m from the ground and you do not catch it, how long will it be in the air? To phrase it slightly differently, if the ball is launched upward with a velocity of 5ms^-1, after how long will it have a displacement of –1.5 m? Here is one approach to solving the problem:

So t is either 1.2 s or –0.2 s. Ignoring the negative value, the answer is that the ball lands about 1.2 s after being thrown. (Ignoring the negative makes sense if you imagine projecting the motion backward in time as if the ball had been thrown up from the floor instead of your hand.)

What about when the ball is not thrown straight up? In this case, the velocity and acceleration of the ball are no longer collinear, and so you cannot simply make calculations with single numbers. However, you can use the trick mentioned in Chapter 5, separating the vectors into components. If you take your basis as the horizontal vector (1 0)^T and the vertical vector (0 1)^T, then the acceleration due to gravity acts only along one of the basis vectors. This means that the component of motion in the horizontal direction is unaffected by gravity. Horizontal velocity is constant. Only the vertical component of motion experiences an acceleration.

Suppose this discussion is applied to cannonballs. A cannon is a device for launching a projectile at an exact angle and speed. The barrel of the cannon is a straight tube that forces the cannonball to travel along a particular path, and the velocity can be calibrated, more or less precisely, according to the amount of gunpowder and the weight of the ball. (This is an example of conservation of energy, which you will look at in a moment.)

As is illustrated in Figure 7.1, if the cannon is aimed at an angle of from the ground, and the ball emerges with a speed u, then the horizontal component of the ball’s initial velocity is , while the vertical component is . What is more, if the length of the cannon is l, then the height of the ball as it leaves the barrel is . How far will the ball travel? Assuming that the ground is flat, the vertical distance traveled by the ball is , so ignoring both the height of the cannon and the horizontal component of the motion, you can use the same technique as before to calculate how long it will be in the air:

Figure 7.1. A cannon firing a projectile at a particular angle.

This is a complicated formula. To make it clearer, substitute in some numbers. Suppose = 30°, so = 0.5. Likewise, suppose the cannon is 2 m long and fires the cannon-ball at 20 ms^-1. The time of flight is

You can use this information along with the (constant) horizontal velocity to calculate the distance traveled:

Using calculus, it is possible to calculate at which angle the ball will travel the farthest. (You might want to try your luck with this question. It isn’t exactly easy, but you have all the tools you need.) You might want to ignore the height of the cannon for simplicity. Assume that the vertical displacement when hitting the ground is zero.) In Exercise 7.2, you are asked to provide a function that will aim a cannon so that its projectile hits a particular point.

These techniques are quite general. They work just as well to calculate the behavior of a person jumping up in a platform game or a slingshot firing pellets in a firing range. The only tricky part is calculating the initial speed of the projectile. This is the topic of the next section.

There are two words used to describe how heavy something is. The most common in English is weight. In physics, this word is used for a force, specifically the downward force on an object due to gravity. It is this (vector) quantity that is measured by, for example, a weighing scale (or scales). The other word is mass, or, equivalently, inertia. You need the language of forces to explain the term precisely, but in this context, you can think of it as a measurement of “how hard it is to move X.” Mass is a scalar quantity, measured in units such as grams, kilograms, or pounds. These units of mass are the units shown on a weight scale because, after all, as long you remain on the same planet, weight and mass are proportional.

A particle’s mass is generally constant—although as is discussed in Chapter 15, this is not so when rockets are considered. More importantly, unlike weight, mass is the same wherever the particle is, whether on a neutron star or in outer space. While an object on the moon weighs approximately a sixth of what it weighs on Earth, its mass is unchanged, so in either place it will take the same amount of effort to get it to the same speed.

So what is mass, anyway? One answer is that it is a fundamental property of matter, going right down to the level of atoms and below. In the simplest terms, it is a measure of how much “stuff” there is in the object. This means that the mass of an object is distributed over its whole volume. In terms of calculating solutions to problems, this might be a problem in itself. Consider that up to now the discussion has been about abstract, point-sized objects, such as particles. How can you be sure that an object with its mass spread over a wider space will behave the same way?

Fortunately, it turns out that you can. To a very good approximation, and apart from rotation, at a particular point inside the object, an object moves along exactly the same path as a point particle. The point inside the object is known as its center of mass or center of gravity. The exact position of the center of mass depends on the shape of the object and the distribution of matter within it, but for a symmetrical object, such as a ball, the center of mass is at the center of the object. This topic is addressed at greater length in Chapter 13.

Mass tends to be most useful in calculations when it is combined with other quantities. One particularly important value is momentum, which is the product of a particle’s mass and velocity. As the product of a vector and a scalar, momentum is a vector, parallel to the velocity.

You can think of momentum as a measure of “how hard it is to stop X.” It is much more difficult to stop a 10-ton truck traveling at one mile per hour than it is to stop a toy car traveling at 15 miles per hour. This is why in feats of strength people are able to pull a truck with their teeth. Although it requires a huge effort to get the thing moving, once it is under way, its own momentum helps to keep it going.

The most important thing to know about momentum is that it is conserved. This means that in the absence of any external influences on a particle—or for that matter on a whole system of particles—the total momentum will be unchanged.

When you are dealing with cannonballs, this is not a very useful thing to know. After all, a cannonball does have an outside influence—the force of gravity. This means that the momentum of a cannonball changes from moment to moment as it arcs through the air. But again, this only applies to the vertical momentum. Horizontally, perpendicular to gravity, velocity and momentum are unchanged. Still, momentum does not really come into its own until you start looking at collisions.

Energy is a measure of how much an object can change its environment. The more energy a particle has, the more effect it can have on the rest of the world. A cannonball lying on the ground can’t do anything to anyone, but one flying through the air can knock down a stone wall. Energy is a scalar quantity, measured in a unit called the joule (J), which is equal to 1 kg ms^-1 (one kilogram-meter per second). In addition to the joule, another unit is used to measure energy units. This is the calorie. As it stands, however, in the world today, use of this term is often restricted to problems concerning food (as in a calorie of nutrition).

Energy can take a number of different forms. Here are a few:

There are many more types of energy, but all of them can be sorted into two categories. One is kinetic. Kinetic energy, such as heat and electricity, is actually doing something. It is able to do so with movement. Heat is a large-scale view of the kinetic energy of the atoms and molecules in a substance, and electrical energy is the result of the movement of electrons (or other charged particles) in a conductor.

The other form of energy is potential energy. Potential energy represents the ability of an object to act, given a change of circumstances. Potential energy is usually relative. For example, chemical potential energy depends on the particular chemical reaction involved. Gravitational potential energy depends on relative heights. Elastic potential energy is a little different, being entirely a property of a particular spring.

Like momentum, energy is conserved within a system, apart from the action of any external force. In fact, in certain cases you can say energy is conserved even when external forces do act, when these forces are included in your energy calculations. Gravity is an obvious example. The force of gravity does not really count as an “external” force since you take it into account in the form of gravitational potential energy. (All potential energies are associated with some kind of force.)

Conservation of energy allows you to make calculations about different parts of a situation using different techniques. For example, when dealing with the cannonball, one of the problems you couldn’t solve was determining the initial speed of the ball as it leaves the cannon. Using conservation of energy and a number of known facts, you can theoretically calculate this speed.

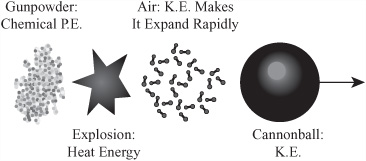
For starters, a chemical reaction between the gunpowder and oxygen in the air causes the cannonball to be propelled outward. The reaction converts some of the chemical potential energy of the gunpowder into heat, giving kinetic energy to the molecules in the air behind the cannonball and causing them to expand rapidly. As illustrated by Figure 7.2, expansion transfers kinetic energy to the cannonball. This means that if you can calculate the energy given off when a quantity of gunpowder is ignited, you also might be able to calculate the energy of the cannonball.

Figure 7.2. The energy transfer during the firing of a cannon.

Of course, in real life, energy transfer is not perfect. A great deal of the heat given off by the gunpowder is absorbed by the surrounding air. This means that the transfer of energy is not 100% efficient. However, you can experiment to discover the particular efficiency.

Another important issue is that, while the cannonball is energized by the reaction, in accordance with the law of conservation of momentum, the cannon itself is propelled backward. The explosion within the cannon counts as an “internal force.” If the total horizontal momentum of the cannon and cannonball is zero before the gun fired, it must be zero afterward. (This does not hold for the vertical momentum, because gravity is acting on the ball and the cannon.) As a result, if the cannonball has a forward momentum p after the explosion, the cannon must have a momentum of –p to compensate.

Suppose the cannonball has a mass of 2 kg and the cannon has a mass of 200 kg. After the gun fires, if the cannonball has a horizontal speed of 30 ms^-1, its momentum is 60 kg ms^-1. Therefore, the cannon must have the same momentum in the opposite direction, which means that its speed must be = 0.3 ms^-1. This is the classic “recoil” phenomenon. Notice that because the cannon is so much heavier than the ball, its speed is much less than the speed of the ball it is firing.

Another consideration is the kinetic energy involved in the explosion. For simplicity, assume that the cannon is aimed horizontally. The kinetic energy of the cannonball after firing is 0.5 × 2 × 30² = 900 J. The kinetic energy of the cannon is 0.5 × 200 × 3² = 9 J. Although the momentum in both directions is equal, the difference in speed makes a major difference to the energy. The energy of the cannon is significantly less than the ball. Nevertheless, it does have some energy. If the cannon is braced to prevent it from moving backward, the ball will emerge faster! All the energy that previously went into moving the cannon backward is now available to give extra kinetic energy to the ball, which means that the ball will have approximately 909 J instead of 900 J. Its speed will be equal to roughly .

The law of conservation of energy gives you different ways to approach a ballistics problem. Ignoring air resistance, after a projectile is flying freely, its energy must remain constant. When it flies up, kinetic energy is transformed to gravitational potential energy (g.p.e.), and when it flies back down, g.p.e. is converted back into kinetic energy. You can use this fact to perform many of the same calculations performed previously. For example, you can ask how high the ball will climb.

As before, suppose the cannon fires the cannonball at 20 ms^-1. Suppose also that the cannonball has a mass of m. The ball’s initial kinetic energy is therefore 400 m. You’ll measure g.p.e. from the muzzle of the cannon, so at the point at which the ball leaves the cannon—its g.p.e.—is 0. Therefore, its total energy (the sum of the kinetic energy and g.p.e.) at all times during the flight must be 400 m.

Assume that the ball is fired straight up (not a wise move when you consider that the ball lands at the same speed it was fired!). At the highest point of the motion, the ball must have a kinetic energy of 0, so its g.p.e. will be 400 m. From the formula for g.p.e., given that mgh = 400 m, h = 40 meters (m). The highest point reached by the ball is 40 m above the muzzle of the cannon. Notice that the mass term cancels out on the two sides of the equation, leaving a height independent of the mass of the ball. Since the trajectory of a projectile is independent of mass, this is to be expected.

If the cannon is fired at an angle, again you have to deal with the motion in horizontal and vertical components. Suppose as before that the cannon is at 30° to the horizontal, so its (constant) horizontal velocity is . At the top of the motion, vertical velocity is 0, but horizontal velocity is unchanged, so the kinetic energy is 1/2 × m × 1.73² = 150m J. Therefore, since the total energy must still be 400 m, you have:

Both of these values need to be adjusted to account for the difference of height above the ground. Try solving the same problem using the equations of motion and see if you get the same answer.

Conservation of energy or momentum considerations will not tell you anything about time. They will not tell you how long anything takes to happen. But in many situations they will enormously simplify calculations.

Write a function named javelin(throwAngle, throwSpeed, time) that calculates the position and angle of a javelin over time.

The function should return an array of two values: a vector (array) representing the position of the javelin at time time after firing and the angle it makes with the horizontal. During its flight, a javelin is more or less oriented along the tangent to the curve. In other words, it is parallel to the velocity vector.

Write a function named aimCannon(cannonLength, muzzleSpeed, aimPoint) that will return the correct firing angle for a cannon if it is to hit a particular point.

Your function should take two scalar arguments, the length of the cannon and the firing speed. It should also take one vector (array) argument, the target position relative to the base of the cannon. It should calculate the best angle at which to aim the cannon so as to hit the point. It should return this angle in either degrees or radians (your preference). In some cases, it may not be possible to hit the target. If this occurs, you should return an error message of some kind. In other cases, there may be more than one possible firing angle. If this occurs, you can choose any valid angle.

Write a function named fireCannon(massOfBall, massOfCannon, energy) that returns the speed of the cannonball as it emerges from the barrel.

This function should use the law of conservation of momentum to calculate the speeds of both the cannonball and the cannon after it is fired. Assume that the variable energy rep resents the total kinetic energy after firing. In other words, chemical energy from the gunpowder is not lost to heat.