Mathematicians divide the world of numbers into several subsets. The first numbers to be recognized were the counting numbers, or natural numbers, which are represented by the symbol N. These are the numbers that children usually learn (1, 2, 3, 4,...). In addition, there is the number zero (0). Each of these can represent a distinct number of “things.” When you add the negative numbers, you have the set of integers, represented by the symbol Z. With the integers, however, a new domain opens out, for negative numbers are brought into the picture.

What, then, is a negative number? You can think about negative numbers in terms of a transaction. Consider a situation in which you have 5 marbles. You are playing with another person, Anne, who has 4 marbles. When you give Anne 2 marbles, she gains 2 marbles, but it is also the case that she is giving you –2 marbles. Either way, you add 2 marbles to one side and subtract 2 from the other.

Given this beginning, you can extend activities to consider multiplication. Think about negative numbers in terms of an operation of “the other way around.” Then you can see why two negative numbers multiplied together give a positive number. You give Anne 2 marbles, which is “the other way round” to her giving you 2 marbles. Since she gave you –2 marbles, if you do this –2 times, it’s the other way round from her doing it 2 times, so it’s the other way round from –4, giving you +4.

If this sounds confusing, the confusion explains why it took centuries for people to accept the idea of negative numbers. The problem was so difficult that fractions, the quotients of two integers, were accepted sooner. First there were the fractions of 1, such as ½ and 1/3. These are in many cases the reciprocals of the natural numbers, as when 2/1 becomes 1/2. After the reciprocals, other simple fractions arose. These were fractions between 0 and 1, such as 2/3. Then came the vulgar fractions, fractions greater than 1, such as 5/4. At the end of the line, you have the complete set of rational numbers, symbolized by Q, which includes both positive and negative fractions, as well as the integers. The integers are included with the rational numbers, because they are viewed as a special kind of fraction that has a denominator of 1.

Beyond the rational numbers, you have the irrational numbers. Such numbers cannot be expressed by the quotient of two integers. For a long time it was thought that such numbers did not exist, but Pythagoras proved that at least one number, the square root of 2, was irrational. Since those days (roughly 550 B.C.E.), the field has expanded. Mathematicians now acknowledge that there are fundamentally more irrational numbers than rational ones.

The rational and irrational numbers together form the set of real numbers, represented by the symbol R. In addition, however, there are other kinds of numbers, such as the complex numbers. These numbers include a multiple of the imaginary number i, which represents the square root of –1. While these numbers are beyond the scope of this chapter, they are dealt with in Chapter 18, which discusses quaternions.

Numbers can be represented many different ways. Consider the number 5. You can represent it geometrically, as a pentagon, but you can also represent it as a set of 5 dots. You can present it physically, as 5 beads on an abacus. Still another (and common) approach is to use the symbol “5,” which is defined to mean what you want it to mean. Each of these representations has its own advantage. For example, if you use beads, to perform operations such as adding and subtracting, you simply count beads back and forth. On the other hand, when you get to larger numbers involving many beads, using symbols has an advantage.

As it is, it is not possible to have a unique symbol for each number. Instead, you use a limited set symbols, combining them to represent a given number, no matter how big. You do this by means of a base system. To create a base system, you choose a number b as a base. Then to represent a number n in the base b, you employ a recursive algorithm. Here is a pseudocode example of how this happens:

function numberToBaseString(Number, Base)
   if Number is less than Base then set Output to String (Number)
   otherwise
      || Find the remainder Rem when you divide Number by Base
      set Output to Rem
      set ReducedNumber to (Number - Rem) / Base
      set RestOfString to numberToBaseString (ReducedNumber, Base)
      append RestOfString to the front of Output
   end if
  return Output
end function

In the numberToBaseString () function, recursion is used. As the name implies, this function converts a number into a string. The function takes two arguments, Number and Base. If you supply 354 as the argument for Number and 10 for the argument for Base, the remainder, when 354 is divided by 10, is 4. This is the number of “units” in 354. The number 4, as the remainder, is written into the output. Next, the remainder is subtracted, resulting in 350, and this result is divided, once again, by 10. By the definition of a remainder, the division is exact, and the answer is 35. This result, 35, is fed into the algorithm again. The remainder is 5, which is the number of “tens” in 354. With another iteration, 3 results, the number of “hundreds.” Putting everything back together, a string is generated, “354,” which is the number first introduced as an argument. While all of this might sound unnecessary, it is important to keep in mind that its purpose is to explore recursively the difference between the number 354 and its representation in the base 10. (Appendix A offers additional discussion of this topic.)

If you perform the operation in reverse, using a string as an argument, you find the value of the number. The baseStringToValue() function shows how this is so:

function baseStringToValue(DigitString, Base)
   if DigitString is empty then set Output to 0
   otherwise
      set Output to the last digit of DigitString
      set RemainingString to all but the last digit of DigitString
      set ValueOfRemainingString to
          baseStringToValue (RemainingString, Base))
      add Base * ValueOfRemainingString to Output
   end if
   return output
end function

When you write a number in base notation, you designate a slot, or base position, for each digit in the number. Consider the number 2631, base 10. The first number, 1, is given by the base to the zero power (which is 1) times the number. The second number, 30, is given by the base to first power (10) times the number (3). The third number, 600, is given by the base to the second power (100), again times the number (6). The process goes on. Rendered as a sequence of additions, you arrive at an expression of this form: 2 × 1000 + 6 × 100 +3 × 10 + 1 × 1.

There’s nothing special about using 10 as a base, but since computers use base 2, base 10 might not be the best choice to use as an example in the current context. Still, base 10 has its virtues, one of which is that humans have 10 fingers to count with. Because 10 is a multiple of 2 and of 5, it’s fairly easy to determine whether a number written in decimal notation is divisible by these two numbers. This is an advantage. On the other hand (no pun intended), it’s much harder to tell if it’s divisible by 4 or 7. However, there are some fairly simple tests for divisibility by 3 or 9, and it’s also easy to divide a number written in base 10 by 2 or 5.

What if you use some other base? Consider, for example, base 12. This base is familiar, in part, because it has been extensively used for currency and measuring, resulting in the familiar system of feet and inches. It makes it easy to divide numbers by 2, 3, 4, or 6. Another is base 60, used in clocks, along with 12 hours. Still another is base 360, used in measuring angles. However, if the last two are to be used properly, they require a lot of individual symbols. The Babylonians used this base, but apparently responding to the complexity of the undertaking, they subdivided its values using a base 10 system. Although very logical, base 12 never caught on except in limited ways.

Base 2, or binary, on the other hand, turns out to be useful in many ways and has found many advocates. In base 2, you represent numbers by powers of two. Using the base positions discussed earlier, the number 11 in base 2 is written as 1011, or 1 × 8 + 0 × 4 +1 × 2 + 1 × 1. As with base 10, as long as you work with integers, representing numbers in base 2 can be done uniquely. Another feature of base 2 is that while you need far more digits to represent any given number, you only need two symbols to do it. For example, 1 is 1, 3 is 11, and 5 is 101. As people learn in a computer architecture course, this way of relating numbers allows you to speak of 1 as “on” and 0 as “off,” and this is the basic (binary) language of digital circuits.

Base 2 requires two symbols, but another base common in computer operations requires 16. This is hexadecimal, which uses the standard decimal symbols 0–9, added to six others, the letters A–F, which stand for 10–15. In hexadecimal, F1A represents 15 × 256 + 1 × 16 + 10 × 1, or 3866. Converting between binary and hexadecimal is quite simple, since each hexadecimal symbol can be translated directly into four binary symbols: F1A translates to 1111 0001 1010.

Because binary can be conveniently represented by two symbols, 1 or 0, or on and off, it’s an ideal system for computers. As has been said many times, a computer thinks only in numbers, and numbers are represented by sets of “switches.” Each switch represents one bit of information, and each bit can be either “on” or “off.” (The word bit is a shortened term for the expression “binary digit.”) With eight such switches (bits), you can represent any number from 0 to 255. With 32 switches (bits), you can represent any number up to 4294967295. With 64 switches (bits), you can represent any number up to 18,446,744,073,709,551,615. This is also known as a “quad word.”

The computer’s native environment is designed to perform calculations very fast with any number using base 2, and this is relative to the number of bits of the processor. A 64-bit machine can handle far bigger calculations than a 32-bit one. Not all bits are used, however. Usually, one bit is set aside to represent whether the number is positive or negative. As a result, a 32-bit machine processes numbers from –2147483647 to 2147483647, instead only a positive range of numbers up to 4294967295.

Since performing operations like addition and multiplication is so easy, binary computations are especially fast. Here is an algorithm that adds two numbers represented as strings in binary:

function addBinaryStrings(b1, b2)
   //pad out the smaller number with leading
   //zeroes so they are the same length
   set Output to ""
   set CarryDigit to 0
   repeat with Index = the length of b1 down to 1
      set k1 and k2 to the Index’th characters of b1 and b2
      if  k1 = k2 then
         // the digits are the same, so write the current carry digit
         set WriteDigit to CarryDigit
         set CarryDigit to k1
         // if k1 and k2 are 1 then you are going to be carrying a digit
         // if they are 0 then you won't.
      otherwise
         // the digits are different,
         // so write the opposite of the current carry digit
         set WriteDigit to NOT(CarryDigit)
        // leave the carry digit alone as it will be unchanged
      end if
      append WriteDigit to the front of Output
  end repeat
  if CarryDigit = 1 then append 1 to the front of Output
  return output
end function

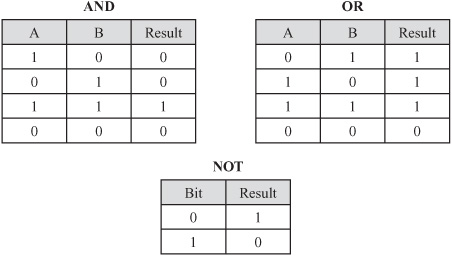
This algorithm is worth examining because the operations it presents are the key to how computers work. In binary, you have 01 + 01 = 10, and 01 + 10 = 11. Speed is augmented because each can be added according to whether digits are the same or different (either 0 or 1). It is not necessary to worry about their values within a large range of values. Since it’s easy to implement in the computer’s hardware, manipulating integers is a relatively simple operation for a computer. Fundamental to this process are the logical operators AND, OR, and NOT, which combine binary (or Boolean) digits together in different ways.

If two values, A and B, are binary digits, as Figure 1.1 illustrates, the AND, OR, and NOT switches result in three primary ways of controlling a computer’s logic. With A AND B, the resulting bit is 1 if and only if both A and B are 1. With A OR B, the resulting bit is 1 if A or B is 1, or if both are 1. With the NOT operation, the result is 1 only if the bit is set to 0.

Figure 1.1. Fundamental Boolean operations on bits.

Multiplication in binary is also straightforward because it combines two simple operations, multiplying by 2 and adding. Just as you can multiply by 10 in decimal, you can multiply by 2 in binary by shifting the digits of the number by one place. Consider, for example, that 6 in binary is 110. If the bits are shifted one place to the left, 12 results, for 12 in binary is 1100.

Thus far, the focus has been on integers, but base notation can be used to represent non-integers, also. The essential activity in this respect is to count down or up from 1. To accomplish this, a marker is used. The marker is referred to as the radix point. The radix point establishes the point at which to start counting. To work with decimal numbers, the radix point is called the decimal point, and the first column after the decimal point represents tenths, the second is hundredths, and so on. In binary, the first column after the radix point represents halves, the second quarters, and so on. Given this scheme of things, the number 1⅜ is represented in binary as 1.011 (1 + ¼ + ⅛).

But there is a problem with this system, which is that not all fractions can be represented this way. In decimal, it is troublesome representing ⅓, because this fraction cannot be expressed as a sum of tenths, hundredths, and so on. It turns out to be the limit of the infinite series You express this by writing 1/3 in decimal as 0.333....

In binary, the situation is even worse. You cannot express any fraction whose denominator is divisible by any number other than 2. Consider, for example, that in decimal, ⅕ is exactly 0.2. In binary, however, it is the infinitely repeating number, 0.001100110011.... Because such numbers have no definitive termination point, computers have trouble with them.

There are two ways to get around this problem. One is to forget radix points and instead to represent the fraction in terms of its constituent integers, the numerator and denominator. Then every rational number can be represented exactly, without any troublesome repeating digits. Unfortunately, there are disadvantages to this as well. If you add ½ and ⅓, the answer is expressed as follows: 5/6. ⅚ + 1/7 = 41/42. 41/42 + 1/11 = 493/462. This is known as an incompatible fraction. With such a fraction, the denominators have no common factor (covered more extensively in Chapter 2), so as you work with the fraction, you end up increasing the complexity of the denominator. As a result, it is easy to go above the computer’s maximum size for integers. Even if the maximum is not reached, the computer slows down as it carries out its calculations with increasingly bulky numbers. Except in very special cases, then, approaching fractions in this way is not a sensible move.

Another problem with this approach is the existence of the irrational numbers, which can’t be expressed exactly as a fraction. Instead, you are forced to find an approximation. To arrive at an approximation, computers use the base system to represent non-integers, and round the number to the nearest digit.

There can also be problems with this, however. Consider what occurs if a fixed-point representation of numbers is used. With this approach, a fixed set of digits (eight, for example) is used after the radix point. With only a limited number of bits to play with for each number, each bit added to the end means one less bit to use at the top. As a result, you are limiting how large and how small numbers can be. Allowing the radix point to be altered changes this situation, and this is what most programming languages do. This alternative is called floating-point representation, similar to what is called scientific notation.

In scientific notation, a number is represented by giving the first “significant” (non-zero) digit, and then as many digits as required after that. Then you give an indication of where to place the radix. For example, the number 201.49 could be represented by (20149; 3). In fact, it is represented as “2.0149 e2.” By convention, you start with the radix after the first digit and count from there. You can count forward or backward (for example, 2.0149 e–3 is 0.0020149). The index (e3) number is called the exponent.

Floating-point numbers use a system similar to scientific notation. There are a number of standard formats. One has been established by the Institute of Electrical and Electronics Engineers (IEEE), an organization that has created many standard formats that are used commonly by computer manufacturers. These standards are important for creating a common language between different hardware.

As established in the IEEE standards, if you are working with 32 bits, you use 1 bit for the sign (positive or negative) and 8 bits for the position of the radix point, from –127 (relative to a value of zero) to +127. This gives a total value of 255. The value of the actual number can then go as high as a little under 2¹²⁸. The remaining 23 bits represent the mantissa, or actual digits of the number. Rather ingeniously, because the first significant digit of a binary number is always 1, there is no need to include this digit in the computer’s representation of the number. It is just implicitly there, which provides one more digit of precision. The actual digits of the floating-point representation are correctly called the significand, although the word mantissa is used for this, too.

To explore how numbers are processed by a computer, consider the actions that are taken with two numbers.

This section explores a few functions that are common, in one form or another, to most computer languages: abs(), floor(), ceil(), and round(). Some languages provide these functions with different names, but they work the same, and the fact that they are so commonly provided testifies to their usefulness. In this context, the discussion involves how they are implemented.

function abs(n)
   if n>=0 then return n
   otherwise return -n
end function

Floats to Integers

Three functions are commonly used to convert float to integer values. Their specific purposes are as follows:

• For a number n, the floor() function finds the largest integer less than n.

• For a number n, the ceil() function finds the smallest integer greater than n.

• For a number n, the round() function finds the integer nearest to n.

Figure 1.2 illustrates the actions of these three functions. Each range is represented by a solid line at one end and a broken line at the other. The solid and broken lines represent inclusion. For example, with floor(n)=3, n is greater than or equal to 3 but less than 4.

Figure 1.2. The ranges of floating point numbers that give the answer 3 using the floor(), ceil(), and round() functions.

Each of these functions is useful in different circumstances. The floor() and ceil() functions are easy for the computer to calculate using floating-point representations. If the exponent of the number is 5, then the functions can find the positive integer part (call it p) of the number by taking the first five digits of the significand. If it’s less than 1, the integer part is zero. If it is greater than the number of digits in the significand, then the function does not know the exact integer part. All that is then necessary is to check the sign of the number. If it is positive, then floor(n) is equal to p and ceil(n) is p + 1. If it’s negative, then ceil(n) is –p and floor(n) is –(p + 1).

The round() function rounds to the nearest whole number. This version of rounding is what most people learn in their early studies of math. The round() function finds an integer such that abs(n - round(n)) < 1. Numbers exactly halfway between two integers, such as 1.5, are ambiguous. You define the round() function to round up in such cases. Given that the floor() and ceil() are defined, the round() function can be implemented as follows:

function round(n)
   Set f to floor(n)
   Set c to ceil(n)
   If n - f > c - n then return c // n is nearer c than f
   If c - n > n - f then return f // n is nearer f than c
   Otherwise return c // n is half-way between c and f
End function

While the round() function suffices to illustrate how a number can be rounded, it remains that it is simpler to calculate the value directly from the floating-point representation. Using this approach, you find the integer part p as before. To decide whether to round up or down, you look at the next digit of the significand, which in binary represents the value ½. If this digit is 0, then the fractional part of the number is less than ½, which means that you round down. If it’s 1, then the fractional part is greater than or equal to ½. If it is greater than or equal, you round up. The arbitrary decision to round up halves turns out to be quite handy. If you round them down, and the first digit of the fractional part is a 1, you still do not know whether to round up or down without looking at the rest of the digits.

No matter how precise you make floating-point numbers, they are still not exact except in special circumstances (such as exact powers of 2). This means that a danger exists of introducing errors into calculations that depend on exact precision. In most circumstances, this is not a major problem, but it is not hard to come up with examples where it is an issue.

For example, ask the computer for the result of . Performing the calculation on paper, you see that the answer should be 0, because and 1 × 50 = 50. However, the computer reports that the answer is 7.10542735760100 e–15. Why does this happen? The answer is that when you divide by 50, you end up with a number with a negative exponent. Adding 1 creates a number with an exponent of 0, which means that a whole lot of bits are dropped off the end of the significand. Multiplying back up by 50 does not restore the lost bits.

Rounding errors are a major source of problems when performing complex and repeated calculations, especially “stretch and fold” calculations that involve adding small numbers to larger ones. In general, there is not a great deal you can do about such problems, but in some cases, doing some pre-calculations alleviates the problem a little.

If you know that you are going to drop and then restore bits, to avoid the problem, you might be able to make your calculations in a different order. In the previous example, consider what happens if you perform the calculation as . In this case, dividing by 50 and then multiplying again results in little loss of precision. Simply adding and subtracting a small integer like 50 is not going to change or worsen the situation.

One other issue to notice here is that testing whether two floating-point calculations are equal may also prove to be a problem. Consider what happens if you ask whether . The answer is no, but it should be yes. In general, it is best when checking for equality of two floats to call them equal when their absolute difference is less than a small value. So, instead of saying if x = y, a preferable approach is to say if abs(x - y) < 0.00001.

None of these workarounds solves the rounding error problem completely. If you are doing calculations that require lots of precision, you might have to use specialized calculation algorithms that allow you to retain as much precision as possible. These will be considered more closely in a moment.

Floating-point calculations are also more expensive in terms of computer time than are calculations with integers. For example, you might find that a given processor using floats calculates 2 × 2 a million times over and requires 1.2 seconds. Integer calculations might take under a second. This is a fairly significant difference for such a simple task. One conclusion is that if at all possible, it’s beneficial to use integer calculations to perform the task you are trying, especially in games or other situations where there are a lot of calculations and speed is an issue.

You can use integer calculations even if you are working with fractions. To do so, multiply all numbers by a sufficiently large number at the start, convert to integers, and complete all your calculations before dividing again by the number at the end. Still, while most calculations will work in this way, caution is the best policy. Test your outcomes as you go.

Having said this, it is certainly the case that the difference between floating-point calculations and integer calculations is not as big a deal as it once was. In the early days of floats, the difference in speed was often critical. These days, processors are geared to deal with floats on a hardware level just as they are with integers, so the difference is not usually important. Your time is probably better spent optimizing other areas of your code.

One way to deal with functions requiring great precision is to work with BigInteger classes. Such classes generate specialized objects that store numbers in long arrays instead of using the computer’s processor to store and work with them. Something similar to this action was taken when, previously in this chapter, a binary number was represented with a long string of digits.

When you perform calculations in this way, you are no longer limited by the processor’s built-in number storage. Your array can be as long as you like, limited only by the computer’s memory. As a result, instead of having 32 or 64 bits to represent a number, you might have a trillion bits or more, which should be sufficiently precise to deal with any calculation you could conceivably want to perform. Of course, since you must perform the calculations at the level of your programming language rather than directly within the processor and each calculation involves many more digits, this approach is much slower. However, in situations in which you need great precision (such as detailed physics simulations of hair, water, or fabric), generally you are thinking in terms of letting the computer do the calculations overnight rather than at lightning runtime speed.

BigInteger classes are available for most languages used by scientists. Consider, for example Java, C#, and C/C++. That they are not dealt with specifically in this context does not make a great deal of difference. The mathematical explorations in this book do not require them.

Write a function convertBase (NumberString, Base1, Base2), which takes a string (or array) NumberString, representing an integer in the base Base1 and converts it into the base Base2, returning the new string (or array). Make it handle any base from 2 to 16.

You might want to make special cases for binary and hexadecimal translation to speed up the function.

Write a series of functions for calculating addition, subtraction, multiplication, and division using IEEE-style floating-point numbers. Represent the floats as 32-bit strings (or arrays) of 1s and 0s.

Each function should take two floating-point numbers and return another. Don’t forget the special case when the exponent is zero. You will probably find division to be the most difficult case.