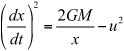Although the word force has been used quite a few times in the preceding pages, as of yet, it has not been precisely defined. Force is a term that is precisely defined in physics, and the study of physics begins with the laws of motion developed by Isaac Newton (1643–1727). Newton’s laws respecting motion and gravitation were presented as universal scientific statements. They have remained valid for hundreds of years, and while it is generally known since the time of Albert Einstein (1879–1955) that they are limited according to the scales of space and time in which they are applied, in everyday use, they are still remarkably accurate.
Even if it provides precise definitions of force, in other respects, this chapter is something of a recapitulation of previous chapters. Among other things, it re-examines terms previously present in the context afforded by the mathematics alone. In the current contexts, you see mathematical techniques put to work by the science of physics.
The term force is used commonly in everyday speech. People refer to the force of an argument, the force of nature, or the force of law. All such uses are both effective for the contexts of their use and highly metaphorical. Such uses suggest an effort or power, and the words “energy” and “work” are used almost interchangeably. In a scientific context, force is a technical term. Newton defined the concept of force precisely with his three Laws of Motion. Force is measured with a unit named after Newton. This is the newton. A newton is defined as one kilogram meter per second per second.
How things move has not always been understood the same way. Before Newton, it was thought that every moving object required some impetus to keep it moving along its path. Unless something is being pushed, it was contended, it will slow down. Among many others, this was a notion introduced by Aristotle (383 B.C.E.–321 B.C.E.). This is not an unreasonable assumption. After all, an automobile stops moving when the engine stops. If you move a toy automobile with your hand, it stops moving if you remove your hand. Even if the automobile has been speeded up or pushed to a high speed, due to friction, it slows and stops after a time. It is only in a setting without friction that Newton’s observations become clear. One such setting is outer space, where there is very little friction.
Having given consideration to how objects move in outer space and elsewhere, Newton formulated his first law. According to this law, an object continues moving at the same velocity unless acted on by a force. This movement includes a velocity of zero. An object that is standing still will remain standing still unless a force is applied to it to set it in motion.
What form this force takes is not stated in Newton’s first law, but for the moment you can think of it as some kind of influence. A particle will continue to travel in the same way unless influenced by some other particle.
As illustrated by Figure 12.1, a body with no forces acting on it is said to be in equilibrium. The sum of the forces acting on it is zero. In this respect, Newton’s first law can be stated as “a body in equilibrium remains at a constant velocity.”
In essence, the Newton’s first law is an early version of a later law of physics relating to conservation of momentum. You implicitly used this latter law when you assumed that the pool balls in the previous chapter would continue to move with the same velocity unless acted on by some friction or colliding with another ball.
Newton presented a second law that is more mathematically involved than the first. While Newton stated the second law in complex terms, stripped to its essentials, it says, When a body is acted on by a force, it experiences an acceleration that is proportional to the force and inversely proportional to the mass of the body. Using mathematics, you can formulate this as follows:
Force on body = mass x acceleration
An alternative way to look at Newton’s second law is to say that the force on a body is equal to the rate of change of the body’s momentum. This is more useful when dealing with forces or masses that change continuously over time, such as centripetal force or the motion of a rocket. Both of these are covered later in this chapter.
Newton’s second law defines the unit of force. It specifies that one unit of force is the force required to accelerate a kilogram mass by 1 ms-1 in one second. As mentioned previously, the newton is the name applied to this force. The abbreviation for one newton is 1N. As you have seen in previous chapters, the acceleration due to gravity at sea level is approximately 10 ms-2. This means that the force of gravity at sea level experienced by a 1-kg mass is approximately 10N. When you feel this force on your body, you feel your weight.
Unlike the equations of motion examined in previous chapters, force is intimately tied in with mass. If you want to throw a 10-kg cannonball, it will take twice the force it would take to throw a 5-kg cannonball. This is where force is related to momentum and the concept of mass can be understood as inertia. Inertia is how much a body resists the action of any force.
How is it that things stand still? By Newton’s second law, if you’re experiencing a constant downward force, you should be accelerating downward. If this does not happen, the reason is that you are in equilibrium. Although there is a force acting down on you, there is another force acting upward. For example, if you are sitting in a chair, then force is acting through the chair you are sitting in to prevent you from going farther down. In turn, the chair is experiencing a downward force from you, but it doesn’t move because it is experiencing an upward force from the floor. That this is so is implied by the first two laws Newton presented. It is formalized in Newton’s third law, which is the most misunderstood of the three. If a body is experiencing a force from some other object, then it exerts an equal and opposite force on that object.
The third law has to be carefully stated because most people get it wrong. They say “every action has an equal and opposite reaction,” but they assume that the two actions are on the same body, which is clearly false. What Newton’s third law actually says is that force is symmetrical. One object can’t exert a force without experiencing a force. Earth pulls you toward itself by the force of gravity, but simultaneously you are pulling Earth slightly toward you.
You don’t notice these effects while on Earth’s surface because, with the huge discrepancy between your mass and Earth’s, the acceleration of Earth due to your gravitational pull is infinitesimally small. What is more, there are many of these infinitesimal forces acting on Earth in all directions, so this tends to cancel their effects. Even the moon, which is much larger than a person, only barely pulls Earth off its orbit about the sun, although its gravitational pull on Earth’s oceans does have a noticeable effect in the tides.
If Newton’s first law is a statement of conservation of momentum for bodies in equilibrium, the third is the equivalent for bodies that are colliding. In fact, aside from conversion of energy into other forms such as heat, it also codifies the law relating to the conservation of energy. Ultimately, while Newton’s first and third laws are different ways of viewing the methods you have already been using to deal with ballistics and collisions, Newton’s second law is a little different. It is a mathematical result that allows you to make calculations about motion. While you will be using the first and third laws from time to time, it is the second law that will concern you most in this and later chapters.
You might have recognized by this point that Newton’s second law is going to encounter problems when dealing with the rigid body collisions you looked at in Part II. With these collisions, you consider that the velocities of colliding bodies change instantaneously at the moment of collision. This implies an infinite acceleration, which requires an infinite force. However, if you have infinite force and acceleration, the velocity at the end of it becomes impossible to calculate in any especially useful way in the context of collision detection.
To deal with this problem, you introduce the concept of an impulse, which is defined as a force acting over a particular time period. It is equal to force × time. Newton’s second law tells you that this impulse is going to be equal to the change in momentum. In a rigid-body collision, an infinitely large force acts over an infinitely short period of time, and these two infinities cancel out to give a finite impulse. As you saw in Chapter 9, using the laws of conservation of energy and momentum, such an impulse is readily calculable.
Note
Recall that there is not really any such thing as a rigid body. Colliding bodies deform as they collide. They also rebound from each other. Since deformation and rebounding require some amount of time to take place in, real collisions always last for some measurable time.
Using these generalizations about impulses, you can rewrite your collision resolution calculations. When two bodies collide, they experience some impulse J in the direction of the collision normal n. This causes a change of momentum that is some multiple of n. You can summarize the event as follows:
mv = mu + Jn
The impulse acts equally and oppositely, so one body experiences J and the other –J. Combining these momentum equations with the energy equations, you can calculate the value of J, which turns out to be
The resulting equation assumes n is unit length, where u is the relative velocity of the two bodies before collision. You might want to see if you can derive this result and make it match with the results of Chapter 9.
In this section, you will look at the force of gravity and how it can be used to explain planetary motion. This story begins with Newton. In addition to his three laws of motion, another discovery of Newton’s was the concept of gravity. While other astronomers, particularly Johannes Kepler (1571–1630), had observed and recorded data that described the motions of the planets, it was Newton who realized that the same principle that causes an apple to fall to the ground could be used to calculate the motions of the planets. It was a revolutionary concept. Accordingly, as Newton understood it, all the planets in the solar system, including Earth, are constantly “falling” toward the sun and each other.
The force of gravity is a universal phenomenon that affects all bodies from the smallest to the largest. Unlike the other “fundamental forces,” gravity is only attractive. Every physical body in the universe attracts every other physical body in the universe. This contrasts with other forces. For example, magnetic forces can attract or repel. In the current state of the universe, however, gravity is one way only.
Gravity works as an inverse-square relationship. The strength of the gravitational attraction between two objects is inversely proportional to the square of the distance between them. The phrase “the distance between them” means the distance between their centers of mass. Expressed as a formula, the relationship is presented as follows:
Here, m1 and m2 are the masses of the two objects, d is the distance between them, and G is a constant, known as the gravitational constant, the value of which turns out to be approximately 6.673000 × 10-11 m3 kg-1 s-2.
Given that gravity works at all scales, you might wonder why you don’t have to take into account the gravitational attraction between all the molecules in each body as well. Fortunately, it turns out that these effects cancel out for a spherical body, and as mentioned earlier, you can treat most bodies as being particles at the center of mass.
Newton deduced the inverse-square relationship by examining the motion of the planets. As the basis of his research, he made use of data associated with Kepler’s laws of planetary motion. By making painstaking and largely accurate observations, Kepler had replaced an understanding of the solar system developed by Nicolaus Copernicus (1473–1543). Copernicus thought the planets revolved around the sun at a constant rate in a circular path. Kepler said that view needed to be modified.
According to Kepler, the motion of a planet relative to the sun is elliptical, with the sun at one focus of the ellipse. Copernicus and others had mistaken the paths of the planets because the eccentricity of the planetary paths are so small. Likewise, Kepler pointed out that speeds of the planets as they travel around the sun are not constant. In fact, the speeds vary quite subtly. The area of the sector of the ellipse swept out during any time period by a planet is constant. Figure 12.2 illustrates how the areas of the two highlighted regions are the same. When the planet is nearer the sun, it moves faster than it does when far away. Figure 12.2 has been drawn in an exaggerated manner to make the effect clear; for planets, the deviation from a circle is minimal.
Kepler’s observations apply to bodies other than planets. In fact, they work for all orbiting bodies, such as moons, comets, and asteroids. Not only that, but they work for meteorites that pass through the solar system without going into orbit. The only qualifier is that rather than moving in an ellipse, they move in a parabola. The law of equal areas continues to apply. Newton worked backward from these observations to realize that they implied an inverse-square law.
All the planets, including Earth, are spiraling slowly in toward the sun. Less stable orbits would have disappeared many billions of years ago and are unlikely to have been suitable for sustaining life. In addition to the Earth, the other existing planets are in nearly stable orbits. Again, however, perfect stability is impossible to achieve. Among other things, the gravitational pull of other planets slightly deflects each one from its orbit, destabilizing it.
The most important aspects of a stable orbit are its period and its semi-major axis. The period, denoted as T, is the time taken for one complete orbit. When one body has a significantly greater mass than the other, as with a planet in orbit around the sun, it turns out that these values are related as follows:
where M is the total mass of the two bodies.
The inverse of the period is called the angular frequency of the orbit, which is 2π times the angular velocity, or the number of orbits in a given time. This gives you the equation of Kepler’s third law:
The value ![]() is also called the mean motion n, and the initial equation can be rewritten in a simpler form as n2a3 = GM.
is also called the mean motion n, and the initial equation can be rewritten in a simpler form as n2a3 = GM.
Another important result is that you can calculate the speed v of a particle when at a particular distance r from the center of the ellipse. This can be worked out by conservation of energy, and gives
Surprisingly, despite all these results, the question of finding the position of an orbiting body at a particular time t cannot be solved by simple algebra or calculus, although it is possible to find a differential equation that can be solved numerically.
An object rotating in a circle appears to be disobeying Newton’s first law. Since the direction of motion is changing, its velocity is constantly changing. However, this correspondence presents no great problem. To achieve the circular motion, there must always be a linear force on the object, directed toward the center of the circle. This force is called the centripetal force and can be calculated precisely. The centripetal force required to keep a mass m rotating at a constant speed v around a radius r is given by ![]() . In terms of the angular velocity ω, the force is ω2r. This relationship will be examined more extensively in the next chapter.
. In terms of the angular velocity ω, the force is ω2r. This relationship will be examined more extensively in the next chapter.
Centripetal force should not be confused with centrifugal force, which is to some extent a myth. A particle moving in a circle is only experiencing a net force inward. However, by Newton’s third law, the particle exerts a force in turn on whatever is causing it to spin. For example, if you whirl an object around on a string, then there is an outward force on the string equal and opposite to the centripetal force. This force on you is called centrifugal force. Similarly, when you whirl a bucket full of water around, the bucket exerts an inward force on the water, which in turn exerts an outward force on the bucket. It is easy to get confused about this phenomenon, and it’s best to ignore centrifugal force altogether and concentrate on the centripetal.
The reason you seem to experience an outward force when moving in a circle is due to Newton’s first law. Your tendency is to keep going in a straight line. It is this inertia that feels like an outward force. But if you imagine standing on a “wall-of-death” fairground ride, it is by being on the inside of the wall, with the wall exerting a force toward the center, that you are held in place. If you were on the outside, you would fly off the wheel. Further, you would fly off tangentially to the wall, not straight outward.
When working in Chapter 7 on ballistics problems, you assumed that the effect of gravity was a constant acceleration. Now you see that this is not true, and the force of gravity varies with height. Over small distances relative to the size of Earth, the difference is negligible, but once you start dealing with objects traveling into space, you have to take variable gravity into account.
In 1945, over a decade before satellites were launched into space, science fiction writer Arthur C. Clarke realized that because the period of a stable orbit varies with distance, at some distance from Earth’s surface, the period of an orbiting satellite will be exactly one day. This means that if the satellite orbits parallel to the equator, it will continuously remain over the same point on Earth’s surface. Envisioning a network of such satellites used for telecommunications, Clark’s speculations turned out to be right on the mark. In part inspired by his ideas, geo-stationary satellites are at the heart of telecommunications, surveillance, and GPS technology.
You can calculate the correct height of a geo-stationary satellite by noting that, as with any orbiting body, it must experience a centripetal force equal to the gravitational force. This gives you the following equation:
If the satellite has a period of T, then you have ![]() , so
, so
To this equation, you plug in values for Earth. Earth has a mass of about 6 × 1024 kg. The sidereal day for Earth is 86164 seconds. A sidereal day is the time taken for Earth to complete one rotation relative to a distant star. Earth’s sidereal day is shorter than a solar day, which is the time to complete a rotation relative to the sun. Since Earth is orbiting around the sun, this adds a little extra relative spin. As a result, you get a value for r of 42168 km.
In current science fiction, one speculative prospect involves a space elevator, which is a long fiber connecting a geo-stationary satellite and its corresponding point on the ground. Once in place, such an elevator would vastly reduce the energy needed to get into space. As interesting as this prospect might be, the technical problems are immense. Among other things, the weight of the fiber alone would be immense, as well as the danger to and from aircraft. Likewise, although the satellite is in geo-stationary orbit, the connecting cable is not, and one result of this is that it acts as a drag on the satellite, tending to pull it out of orbit. Having said all this, many research groups are working on overcoming these obstacles.
The discussion thus far has not provided the tools to deal with rocket travel properly. The key to successful rocket travel is that the mass of the rocket decreases as its fuel is used up, and working comprehensively with an object whose mass changes over time must wait a few chapters. However, at this point, you can make a start. One approach is to consider a very fast cannonball. While such an object moves at great speed into space, its mass remains constant. How does such an object behave?
To investigate the behavior of the cannonball, consider first that the mass of the cannonball is much less than Earth’s, so you can assume that Earth does not move significantly as a result of the gravitational pull of the cannonball. Likewise, assume the ball is fired vertically into space from sea level.
You can solve this problem of what happens after the cannonball is fired by means of energy considerations. At a distance x from the center of Earth, the cannonball has a gravitational potential energy of ![]() . If its initial upward speed is u, then you know that
. If its initial upward speed is u, then you know that ![]() at every instant of the motion. This gives you a differential equation:
at every instant of the motion. This gives you a differential equation:
Differential equations are not, in general, easy to solve exactly in some algebraic form, and this is no exception. However, it does mean that given a particular initial position and speed for the cannonball, you can calculate its motion over time by incremental steps. The moveCannonBall() function is constructed to carry out this operation:
function moveCannonBall(currentHeight, initialSpeed, timePeriod, G, M)
set currentSpeed to sqrt(2*G*M / currentHeight
- initialSpeed * initialSpeed)
return currentSpeed * timePeriod
end function
Write a set of functions that will allow a system of planets to move under gravity.
You can do this a number of different ways, but the mathematics is the same. At each time-step, calculate the total force on each planet due to the gravitational fields of the others. Then convert this to a linear acceleration. Be careful to base your accelerations on positions at the beginning of the time step. Don’t use moved positions. See if you can set up a planet to orbit smoothly.
Little code has been presented in this chapter. The reason for the lack of code is that it has been necessary to restate earlier results in a new form. Given this new phase of understanding, however, you can now use the language of forces and Newton’s laws much more extensively in your programming efforts. In the next chapter, you will continue the study of orbits by looking at angular motion and particularly angular momentum.