3.2 LONG RANGE HYDRO THERMAL SCHEDULING
Let a power system consist of one large hydel plant and one thermal plant say. The two plants cater to the total system load PD.
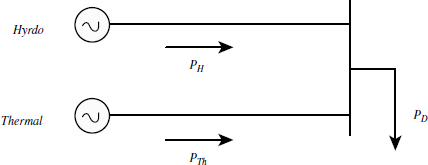
Fig 3.1 A power system consisting of a hydel and a thermal Plant.
The hydro plant can generate power PH more than power demand PD for a limited time t. That is,
However, the energy available from the hydro plant is insufficient to meet the load because of the water constraints.
Let tmax be the number of hours required for an optimization solution (week/month/year) say.
The hydro energy produced is less than total energy required. The difference in energy shall be supplied from the thermal plant.

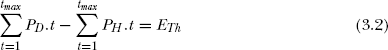
Let the thermal plant be operating for tTh hours, where tTh < tmax. The energy produced by it in tTh hours is:

Using Eqns. (3.2) and (3.3), the energy equivalent constraint can be written as:

It can be understood that the hydel plant is working for total tmax hours in the considered period. However, the thermal plant is working only for tTh hours. The fuel cost of the thermal plant can be written as
In the span of tTh hours, the total energy cost is:
Now, the problem is to minimize the value Eq.(3.6) subject to equality constraint Eq.(3.4) using Lagrangian technique, the constrained objective function can be written as unconstrained function using Lagrangian multiplier λ as:
Using the Kuhn-Tucker necessary condition for local minima of L, the condition for economic operation can be obtained. The condition can be obtained when the first derivative of L with respect to independent variable PTh is set to zero.
i.e.,

For the period of tTh, when both hydro and thermal generations are available, the economic operation in hydro thermal scheduling can be achieved when Eq.(3.7) is satisfied. The thermal plant is loaded according to Eq.(3.7) and the remaining part of load demand is met by the hydro plant.
3.2.1 Determination of Optimal Contribution of Thermal Plant
Let the total demand PD exist for tmax hours. The PD can be met from thermal and hydro plants. Let ![]() be the optimal generation value of the thermal plant.
be the optimal generation value of the thermal plant.
Fig. 3.2 represents energy diagram for tmax hours.
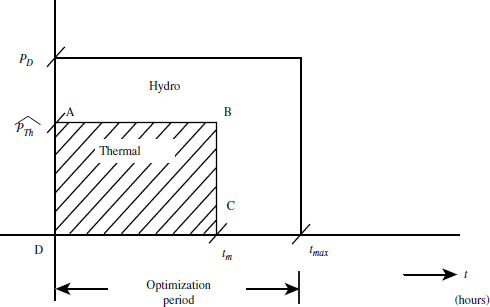
Fig 3.2 Energy contributions of hydro and thermal plant for a specified period
The thermal energy is given by Eq.(3.3) as:
From Fig.3.2, the value of ETh can be obtained by calculating the area of rectangle ABCD as:
From Eq.(3.10),
Using Eq.(3.5),
The total cost of thermal energy generation is:

For minimal thermal energy cost,
Using Eq.(3.13),
From Eq.(3.14)
Note: Eq.(3.15) represents optimal thermal generation, while Eq.(3.11) gives the time tTh for which the thermal plant should be kept in service.
Example 3.1
A power system consists of one thermal and one hydro plant. The load is constant at 100 MW for a period of 45 days. The fuel cost curve of the thermal plant is represented by:
If the total energy produced by the hydel plant in the period is 80,000 MWH, calculate the optimal time for which the thermal plant should be kept in service and optimal thermal generation.
Solution:
Using Eq.(3.5), 50
Optimal thermal generation ![]()
Using Eq.(3.11)

Note: The total load 100 MW for a period of 1080 hours (45 days) shall be met as per the following conclusions.
Total load = 100 MW
Total duration = 1080 hours
In 531.263 hours,
In the remaining period (1080 – 531.263 = 548.737 hours), the total demand of 100 MW shall be met from the hydel plant only.
3.2.2 Short Term Hydro Thermal Scheduling
Let one thermal plant and one hydel plant together meet a total load demand of PD MW. The duration of this run may range from a day to maximum of one week. Knowing the total volume of water available for discharge, the problem lies in the minimization of total cost subject to water discharge constraints.
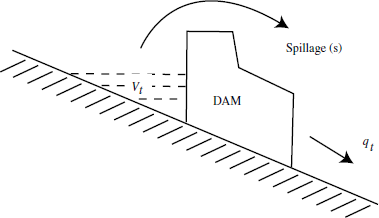
Fig 3.3 Block diagram of a typical hydel plant
Mathematically, the problem is solved as:
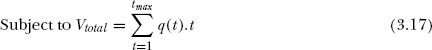
Where Fc = total cost function (in Rs/hr)
PH = Hydro power generation (in MW)
PTh = Thermal power generation (in MW)
t = time interval in the concerned period (day/week)
tmax = Maximum number of hours in the concerned period
Vtotal = Total volume of water discharged in 0 to tmax hours
q(t) = discharge in m3/sec
For the sake of simplifying the problem, the following assumptions are considered.
- The total power demand PD during the period is constant.
- At the begining and in the end, the volume of water in the reservoir is specified.
- Due to technical problems, water cannot be discharged suddenly or stopped suddenly. i.e qmin ≤ q(t) ≤ qmax
- Hydro power generation is a function of discharge q(t).
- The spill-over of water from the dam is zero
i.e S(t) = 0
The equality and inequality constraints and the statement of the problem are given in detail below.
The total cost function is a function of fuel costs of thermal and hydro plants. For a given PD, the total cost function is:
|
where Fc(PTh, PH) |
: |
Total cost function, which is a function of thermal generation PTh and hydro generation PH (in Rupees) |
|
FTh(t, PTh) |
: |
Cost of thermal generation. Computed at t, while generating PTh (in Rs/hr) |
|
FH(t, PTh) |
: |
Cost of hydro generation. Computed at t, while generating PH (in Rs/hr) |
The objective is to minimize FC (PTh, PH)
In Eq.(3.19),
|
FC (PTh, PH) |
= Total cost function |
|
Fth (t, PTh) |
= Fuel cost of thermal plant |
|
γh |
= Constant which converts incremental water into an equivalent incremental cost |
|
W (t, PH) |
= Water discharge to generate hydel power PH in the given time ‘t’. |
It should be remembered that discharge is a function of hydro power generation.
The equality constraint is:
In the Eq.(3.20)
Assuming that there in no spillage, the inequality constraint is:
In the Eq.(3.21),
WTotal = Total water discharge in the period from t = 1 to t = tmax hours.
W(t) = Water discharge during the time ‘t’.
The constrained objective function Eq.(3.19) can be converted into an unconstrained function using Lagrangian technique as:
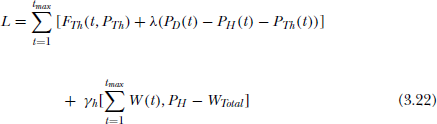
The optimal solution can be obtained by equating ![]()
Similarly optimal scheduling of hydro generation can be obtained by evaluating ![]() using Eq. (3.22),
using Eq. (3.22),
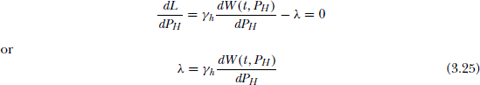
Optimal hydro scheduling is possible when incremental cost of received power(λ) is equal to plant’s incremental cost of generation as:
Eqs. (3.24 and 3.25) are known as coordination equations and can be used for computation.
Algorithm
Step-1: Have an initial guess for λh
Step-2: Set t = 1
Step-3: Assume λdeg
Step-4: The PTh and PH can be obtained using Eqs (3.24) and (3.25)
Step-5: Check if PD – PH – PTh = 0. If this condition is satisfied GOTO Step-6. Otherwise take a new value of λdeg and repeat Steps 3 to 5.
Step-6: t = t + 1 (goto next hour) If t > tmax GOTO Step-7. Else repeat Steps 3 to 5 for new load demand PD.
Step-7: The water withdrawal from hydel plant for total hydel generation during the period should be computed.
Step-8: If the difference between the calculated water withdrawal and scheduled water withdrawal is not within the prescribed tolerance, then γn is adjusted and the procedure is repeated until the criterion is satisfied
Step-9: Print Results, END.
