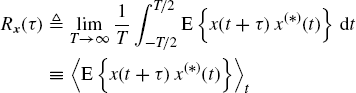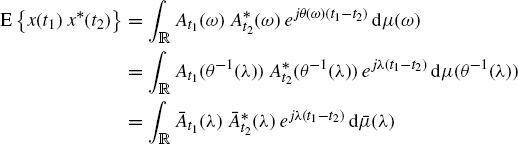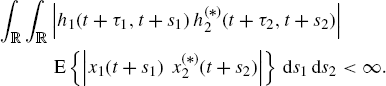1.1 Second-Order Characterization of Stochastic Processes
1.1.1 Time-Domain Characterization
In the classical stochastic-process framework, statistical functions are defined in terms of ensemble averages of functions of the process and its time-shifted versions. Nonstationary processes have these statistical functions that depend on time.
Let us consider a continuous-time real-valued process 
, with abbreviate notation x(t) when it does not create ambiguity, where Ω is a sample space equipped with a σ-field 
and a probability measure P defined on the elements of . The cumulative distribution function of x(t) is defined as (Doob 1953)
where
(1.2) 
is the indicator of the set 
and 
denotes statistical expectation (ensemble average). The expected value corresponding to the distribution 
is the statistical mean
(1.3) 
Analogously, at second-order, the process is characterized by the second-order joint distribution function (Doob 1953)
(1.4) 
and the autocorrelation function
If 
and 
depend on t, the process is said to be nonstationary in the strict sense. If 
does not depend on t, the process x(t) is said to be 1st-order [2nd-order] stationary in the strict sense. If both mean and autocorrelation function do not depend on t, the process is said to be wide-sense stationary (WSS) (Doob 1953).
In the following, we will focus on the second-order statistics of complex-valued nonstationarity processes.
The complex-valued stochastic process x(t) is said to be a second-order process if the second-order moments
exist 
and 
. In Equation (1.6), superscript (*) denotes optional complex conjugation, and subscript 
. That is, 
denotes one of two different functions depending if the complex conjugation is considered or not in subscript x. If conjugation is present, then (1.6) is the autocorrelation function. If the conjugation is absent, then (1.6) is the conjugate autocorrelation function also referred to as relation function (Picinbono and Bondon 1997) or complementary correlation (Schreier and Scharf 2003a). Note that, in the complex case the order of the distribution functions turns out to be doubled with respect to the real case. For example, the joint distribution function of x(t) and x(t + τ) is a fourth-order joint distribution of the real and imaginary parts of x(t) and x(t + τ).
The (conjugate) autocovariance is the (conjugate) autocorrelation of the process reduced to be zero mean by subtracting its mean value
(1.7) 
Even if 
only for zero-mean processes, in some cases the terms autocorrelation, autocovariance, and covariance are used interchangeably. When the terms autocovariance or covariance are adopted, from the context it is understood if the mean value is subtracted or not. In statistics, the definition of autocorrelation includes in (1.6) also a normalization by the standard deviations of x(t) and x(t + τ).
1.1.2 Spectral-Domain Characterization
The characterization of stochastic processes in the spectral domain can be made by resorting to the concept of harmonizability (Loève 1963). A second-order stochastic process x(t) is said to be harmonizable if its (conjugate) autocorrelation function can be expressed by the Fourier-Stieltjes integral
where 
is a spectral correlation function of bounded variation (Loève 1963):
(1.9) 
In (1.8), (−) is an optional minus sign that is linked to 
denotes one of two different functions depending if the complex conjugation is considered or not in subscript x.
Under the harmonizability condition, x(t) is said to be (strongly) harmonizable and can be expressed by the Cramér representation (Cramér 1940)
where χ(f) is the integrated spectrum of x(t).
In (Loève 1963), it is shown that a necessary condition for a stochastic process to be harmonizable is that it is second-order continuous (or mean-square continuous) (Definition 2.2.11, Theorem 2.2.12). Moreover, it is shown that a stochastic process is harmonizable if and only if its covariance function is harmonizable. In fact, convergence of integrals in (1.8) and (1.10) is in the mean-square sense. In (Hurd 1973), the harmonizability of processes obtained by some processing of other harmonizable processes is studied.
If the absolutely continuous and the discrete component of χ(f) are (possibly) nonzero and the singular component of χ(f) is zero with probability 1 (w.p.1) (Cramér 1940), we can formally write dχ(f) = X(f) df (w.p.1) (Gardner 1985, Chapter 10.1.2), where
is the Fourier transform of x(t) which possibly contains Dirac deltas in correspondence of the jumps of the discrete component of χ(f). For finite-power processes, that is such that the time-averaged power
(1.12) 
exists and is finite, relation (1.11) is intended in the sense of distributions (Gelfand and Vilenkin 1964, Chapter 3), (Henniger 1970).
Let x(t) be an harmonizable stochastic process. Its bifrequency spectral correlation function or Loève bifrequency spectrum (Loève 1963; Thomson 1982), also called generalized spectrum in (Gerr and Allen 1994), cointensity spectrum in (Middleton 1967), or dual frequency spectral correlation in (Hanssen and Scharf 2003), is defined as
and if χ(f) and 
do not contain singular components w.p.1, in the sense of distributions the result is that
(1.14a) 
and, accordingly with (1.8), we can formally write
A spectral characterization for nonstationary processes that resembles that for WSS processes (Section 1.1.4) can be obtained starting from the time-averaged (conjugate) autocorrelation function
when the limit exists. Its Fourier transform is called the power spectrum, is denoted by Sx(f), and represents the spectral density of the time-averaged power Rx(0) of the process. The time-averaged autocorrelation function and the power spectrum defined here for nonstationary processes exhibit the same properties of the autocorrelation function and power spectrum defined for wide-sense stationary processes (Wu and Lev-Ari 1997).
1.1.3 Time-Frequency Characterization
The Loève bifrequency spectrum (1.13) provides a description of the nonstationary behavior of the process x(t) in the frequency domain. A description in terms of functions of time and frequency can be obtained by resorting to the time-variant spectrum, the Rihaczek distribution, and the Wigner-Ville spectrum.
The Fourier transform of the second-order moment (1.6) with respect to (w.r.t.) the lag parameter τ is the time-variant spectrum
By substituting (1.6) into (1.18), interchanging the order of the expectation and Fourier-transform operators, and accounting for the formal relation 
, one obtains
(1.19) 
where the right-hand-side is referred to as the (conjugate) Rihaczek distribution of x(t) (Scharf et al. 2005).
By the variable change 
in (1.6) and Fourier transforming w.r.t. τ, we obtain a time-frequency representation in terms of Wigner-Ville spectrum for stochastic processes (Martin and Flandrin 1985)
(1.20b) 
where the second equality follows using (1.11).
Extensive treatments on time-frequency characterizations of nonstationary signals are given in (Amin 1992), (Boashash et al. 1995), (Cohen 1989, 1995), (Flandrin 1999), (Hlawatsch and Bourdeaux-Bartels 1992). Most of these references refer to finite-energy signals.
1.1.4 Wide-Sense Stationary Processes
Second-order nonstationary processes have (conjugate) autocorrelation function depending on both time t and lag parameter τ and the function defined in (1.6) is also called the time-lag (conjugate) autocorrelation function. Equivalently, their time-variant spectrum depends on both time t and frequency f. In contrast, second-order WSS processes are characterized by a (conjugate) autocorrelation and time-variant spectrum not depending on t. That is
(1.21b) 
In such a case, for (*) present, the Fourier-transform (1.18) specializes into the Wiener-Khinchin relation that links the autocorrelation function and the power spectrum Sx(f) (Gardner 1985)
(1.22) 
Condition (1.21a) is equivalent to the fact that the time–time (conjugate) autocorrelation function (1.8) depends only on the time difference t1 − t2. This time dependence in the spectral domain corresponds to the property that the Loève bifrequency spectrum (1.13) is nonzero only on the diagonal f2 = − (−)f1. That is,
where 
denotes Dirac delta. When (*) is present, 
is the power spectrum of the process x(t). From (1.23), it follows that for WSS processes distinct spectral component are uncorrelated. In contrast, the presence of spectral correlation outside the diagonal is evidence of nonstationarity in the process x(t) (Loève 1963). Finally, for WSS processes the Wigner-Ville spectrum is independent of t′ and is coincident with the power spectrum. That is, 
.
Extensive treatments on WSS processes are given in (Brillinger 1981), (Cramér 1940), (Doob 1953), (Grenander and Rosenblatt 1957), (Papoulis 1991), (Prohorov and Rozanov 1989), (Rosenblatt 1974, 1985).
1.1.5 Evolutionary Spectral Analysis
In (Priestley 1965), the class of zero-mean processes for which the autocovariance function admits the representation
is considered, where {ϕt(ω)} is a family of functions defined on the real line (
) indexed by the suffix t and dμ(ω) is a measure on the real line. In (Grenander and Rosenblatt (1957) paragraph 1.4), it is shown that if the autocovariance has the representation (1.24), then the process x(t) admits the representation
(1.25) 
where Z(ω) is an orthogonal process with
(1.26) 
In fact, we formally have
(1.27)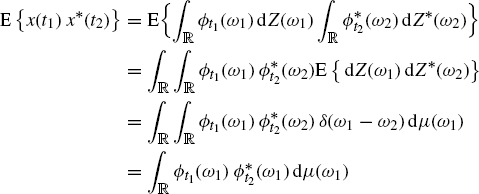 
where, in the last equality, the sampling property of the Dirac delta (Zemanian 1987, Section 1.7) is used.
When the process is second-order WSS, a valid choice for the family 
is 
. The autocovariance is
(1.28) 
which is function of 
. The function 
is the integrated power spectrum. If μ(ω) is absolutely continuous or contains jumps and has zero singular component (Cramér 1940), then in the sense of distributions 
, where S(ω) is the power spectrum (with 
) which contains Dirac deltas in correspondence of the jumps in 
.
The function of t, 
is said to be an oscillatory function if, for some real-valued function θ(ω), it results in
where the modulating function At(ω), as a function of t, has a (generalized) Fourier transform with an absolute maximum in the origin (that is, as a function of t, it is a low-pass function) and can be seen as the “envelope” of x(t). In addition, if the function θ(·) is invertible with inverse 
, then by substituting (1.29) into (1.24) and making the variable change λ = θ(ω) we have
where 
and 
. The process is said to be an oscillatory process and admits the representation
with respect to the family of oscillatory functions
where 
is an orthogonal process with
In fact, by using (1.31) and (1.33) into the autocovariance definition leads to the rhs of (1.30).
Motivated by the fact that, according to (1.30),
(1.34) 
the evolutionary spectrum at time t with respect to the family (1.32) is defined as
(1.35) 
This definition is consistent with the interpretation of (1.31) as an expression of the process x(t) as the superposition of complex sinewaves with orthogonal time-varying random amplitudes 
.
The WSS processes are obtained as a special case of oscillatory processes if 
for all t and ω and 
, or, equivalently, 
for all t and λ. In such a case, the evolutionary spectrum is coincident with 
and WSS processes are expressed as the superposition of complex sinewaves with orthogonal time-invariant random amplitudes (Cramér 1940).
For generalizations and applications, see (Matz et al. 1997), (Hopgood and Rayner 2003).
1.1.6 Discrete-Time Processes
The characterization of discrete-time nonstationary stochastic processes can be made similarly to that of continuous-time processes with the obvious modifications. The harmonizability condition for the discrete-time process xd(n) is
with 
spectral correlation function of bounded variation when 
. Under the harmonizability condition, xd(n) can be expressed as
(1.37) 
where we can formally write 
(Gardner 1985, Chapter 10.1.2) with
Fourier transform of 
to be intended in the sense of distributions (Gelfand and Vilenkin 1964; Henniger 1970, Chapter 3).
The possible presence of Dirac deltas on the edges of the integration domain in (1.36) or for ν = ± 1/2 in (1.38) must be managed, accounting for the periodicity with period 1 w.r.t. variables ν1 and ν2 in (1.36) and w.r.t. variable ν in (1.38). If one delta term is considered, then its replica must be neglected.
The Loève bifrequency spectrum of xd(n) is defined as (Loève 1963)
(1.39) 
Let 
be the discrete-time process obtained by uniformly sampling with period 
the continuous-time process x(t). The (conjugate) autocorrelation function of xd(n) turns out to be the sampled version of that of x(t) at sampling instants 
and 
. The Loève bifrequency spectrum of xd(n) can be expressed as
(1.40) 
Uniform sampling is a linear periodically time-variant transformation of a continuous-time process into a discrete-time process. Since the transformation is time-variant, in general the nonstationary behavior of the discrete-time process can be different from that of the continuous-time one.
1.1.7 Linear Time-Variant Transformations
In this section, linear time-variant (LTV) transformations of stochastic processes are considered. Input/output relations are derived in both time and frequency domains with reference to processes and their second-order moments.
The input/output relationship of a LTV system is given by
where h(t, u) is the system impulse-response function. That is,
(1.42) 
where 
denotes Dirac delta. By Fourier transforming both sides of (1.41), one obtains the input/output relationship in the frequency domain
where the transmission function H(f, λ) (Claasen and Mecklenbräuker 1982) is the double Fourier transform of the impulse-response function:
In (1.43), (1.44), and the following, Fourier transforms are assumed to exist at least in the sense of distributions (generalized functions) (Zemanian 1987).
1.1.7.1 Input/Output Relations in the Time Domain
Let us consider two LTV systems with impulse-response functions h1(t, u) and h2(t, u), excited by x1(t) and x2(t), respectively (Figure 1.1). The output signals are
Figure 1.1 LTV systems –time domain
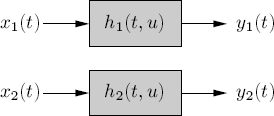
The (conjugate) cross-correlation of the outputs y1(t) and y2(t) can be expressed in terms of that of the input signals x1(t) and x2(t):
(1.46)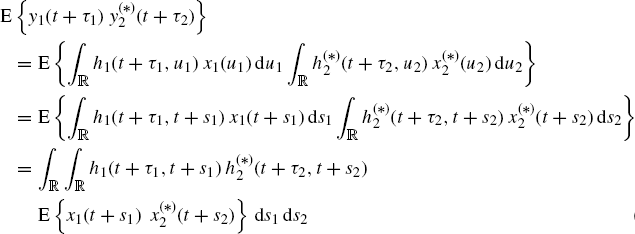 
where, in the second equality, the variable changes 
are made in order to allow, in the third equality, the interchange of integral and expectation operators also when the proof is made in the functional approach (see Chapter 6).
A sufficient condition to allow the interchange of integral and expectation operators is given by the Fubini and Tonelli theorem (Champeney 1990, Chapter 3)
1.1.7.2 Input/Output Relations in the Frequency Domain
The frequency-domain counterpart of the input/output relation (1.45) is (Figure 1.2)
(1.48) 
where Hi(f, λ), i = 1, 2, are the transmission functions defined according to (1.44).
Figure 1.2 LTV systems –frequency domain
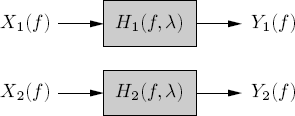
The Loève bifrequency cross-spectrum of the outputs y1(t) and y2(t) can be expressed in terms of that of the input signals x1(t) and x2(t) as follows
(1.49)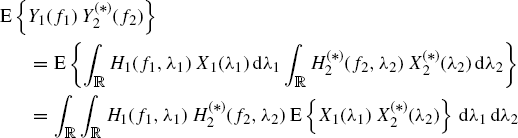 
provided that (Fubini and Tonelli theorem (Champeney 1990, Chapter 3))
(1.50) 