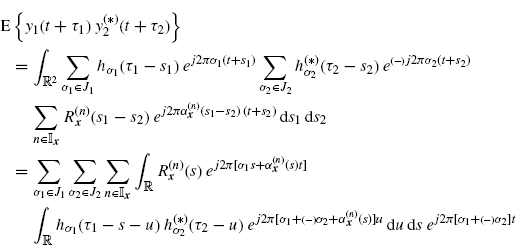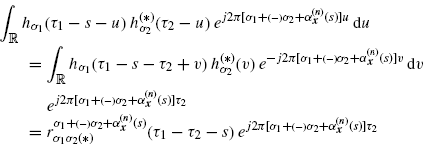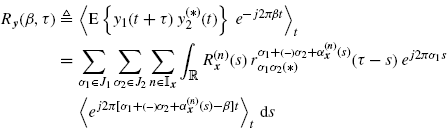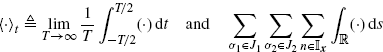3.3 Proofs for Section 2.3 “Linear Time-Variant Filtering of GACS Processes”

3.3.1 Proof of (2.112)

By substituting (2.111) into (2.110) we have

(3.33)

where, in the second equality the variable changes s₁ = s + u, s₂ = u are made. Furthermore, by making the variable change into the inner integral in (3.33), we have

(3.34)

where is defined in (2.113).

By substituting (3.34) into (3.33), we obtain (2.112).

Assumption (1.47) allows to interchange the order of integral and expectation operators (Fubini and Tonelli Theorem (Champeney 1990, Chapter 3)).

3.3.2 Proof of (2.117)

From (2.112) with τ₁ = τ and τ₂ = 0 it follows that

(3.35)

from which (2.117) immediately follows.

To obtain (3.35), under assumptions (2.114)–(2.116), the order of

operations can be interchanged. In fact, the following inequalities hold

(3.36)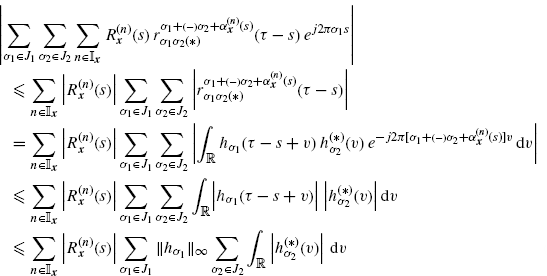

and

(3.37)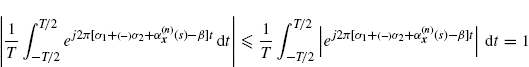

independent of T.

Therefore, conditions (2.114)–(2.116) allow to use the Fubini and Tonelli theorem (Champeney 1990, Chapter 3) to interchange the order of integrals in dt and ds for T finite. Moreover, the same conditions are sufficient to apply the dominated convergence theorem (Champeney 1990, Chapter 4) to interchange the order of limit and integral operations.