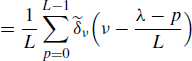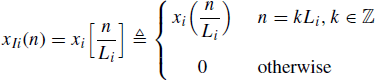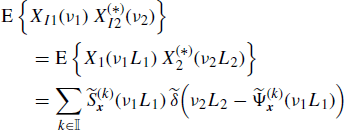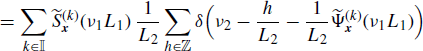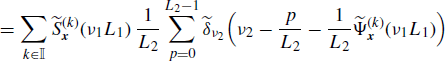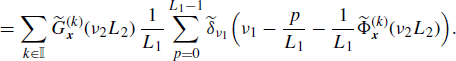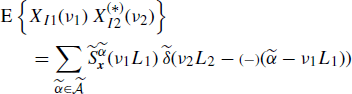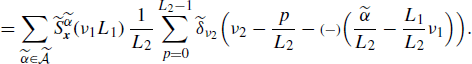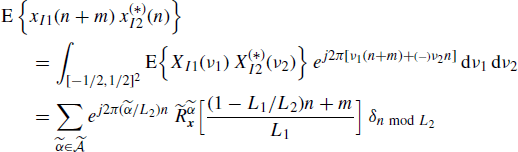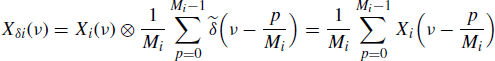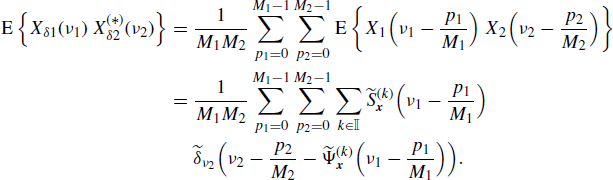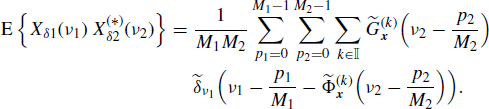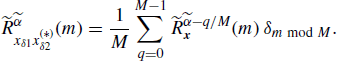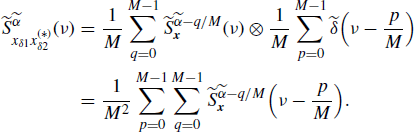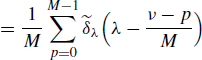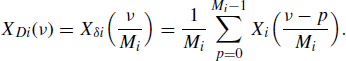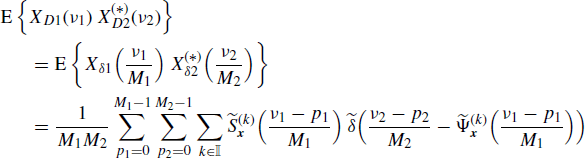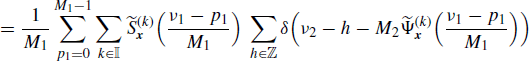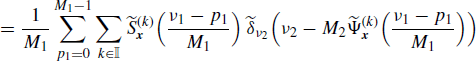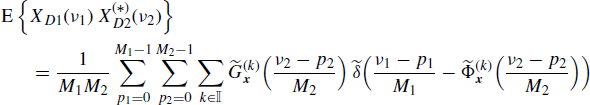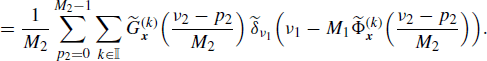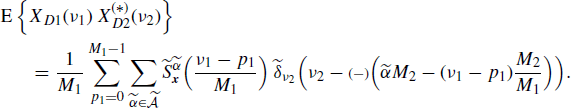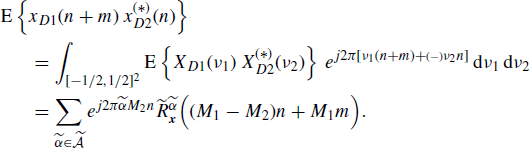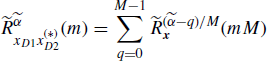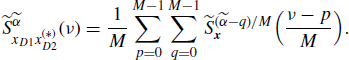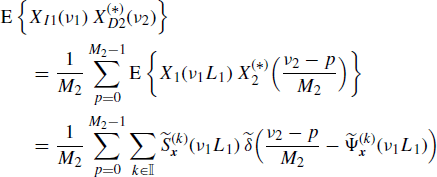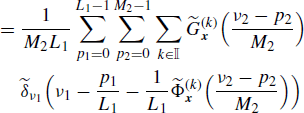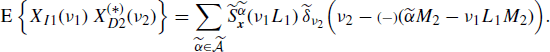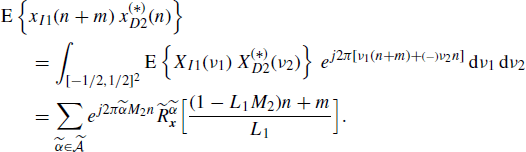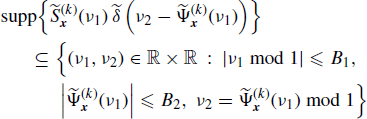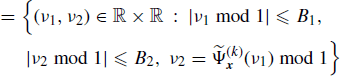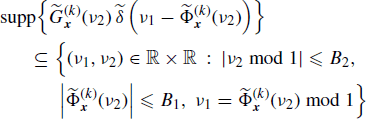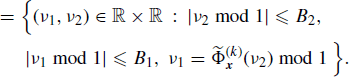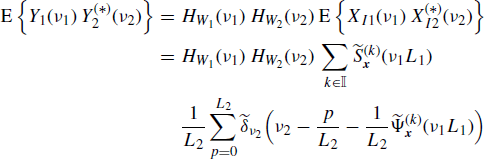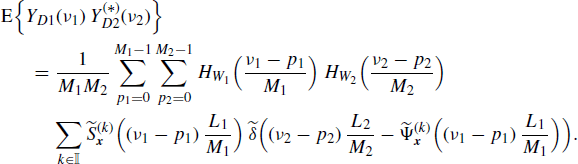4.10 Multirate Processing of Discrete-Time Jointly SC Processes

In multirate digital signal processing, systems constituted by complicate interconnections of interpolators, decimators, and linear time-invariant (LTI) filters acts on input stochastic processes (Crochiere and Rabiner 1981), (Vaidyanathan 1990). Since interpolators and decimators are linear time-variant systems, the stationarity or nonstationarity properties of the input processes turn out to be modified at the output. For example, the expanded version of a WSS process is cyclostationary with period of cyclostationarity equal to the expansion factor (Sathe and Vaidyanathan 1993).

The effects of multirate systems on second-order WSS and cyclostationary processes are analyzed in (Sathe and Vaidyanathan 1993). In (Akkarakaran and Vaidyanathan 2000), conditions that preserve at the output of an interpolation filter the wide-sense stationarity of the input sequence are derived. Moreover, conditions for the joint wide-sense stationarity of the outputs of interpolation filters are also obtained. Higher-order statistics of ACS processes are considered in (Izzo and Napolitano 1998b).

In (Sathe and Vaidyanathan 1993), (Izzo and Napolitano 1998b), and (Akkarakaran and Vaidyanathan 2000), multirate operations on a single process are addressed and no cross-statistics of a process and its expanded or decimated version are considered. Moreover, no cross-statistics are considered between processes obtained by multirate elaborations of the same process with different rates.

Expansions with different rates transforms jointly WSS, jointly ACS, and jointly SC processes into jointly SC processes. An analogous result is obtained by decimation with different rates.

In this section, the effects of expansion and decimation operations on jointly SC processes are analyzed. Specifically, the way in which the Loève bifrequency cross-spectrum of input jointly SC processes transforms into the Loève bifrequency cross-spectrum of the output processes is derived for expansors and decimators which are the basic building blocks of multirate systems. The class of the jointly SC processes is shown to be closed under linear time variant transformations realized by interconnecting expansors and decimators. The case of input jointly ACS processes is analyzed in detail. It is proved that even if the input processes are jointly ACS, in general the output processes are jointly SC. Known results for ACS processes are obtained as special cases.

The problem of suppressing imaging and aliasing replicas in the Loève bifrequency cross-spectra of interpolated or decimated processes is addressed. Specifically, the reconstruction (but for two frequency scale factors) of an image-free Loève bifrequency cross-spectrum of two jointly SC processes when they passes through two interpolator filters is considered. Then, the reconstruction of a frequency-scaled version of the Loève bifrequency cross-spectrum of two jointly SC processes starting from the outputs of two decimation filters is addressed. Finally, the problem of reconstructing a frequency-scaled image-and alias-free version of the Loève bifrequency cross-spectrum of two jointly SC processes starting from their fractionally sampled versions is treated.

4.10.1 Expansion

4.10.1.1 LTV System Characterization

The L-fold expanded version of the discrete-time signal x(n) is defined as

(4.237)

Thus, it results that

(4.238)

from which it follows that the Fourier transform X_I(ν) of x_I(n) is given by

(4.239)

In Section 5.11 it is shown that expansion is a linear time-variant transformation (Figure 4.16)

(4.240)

with impulse-response function

(4.241)

and transmission function

(4.242a)

(4.242b)

(4.242c)

where

(4.243)

and the subscript in notation and indicates the variable with respect to which periodization is made and needs to avoid ambiguities when a function of two variables λ and ν is considered.

The function H_I(ν, λ) is periodic in ν with period 1/L and periodic in λ with period 1. Systems performing L-fold expansion are a special case of discrete-time FOT-deterministic LTV systems (Section 4.3.1) not LAPTV.

4.10.1.2 Input/Output Statistics

Let x_Ii(n) be the L_i-fold expanded version of x_i(n), (i = 1, 2). That is

(4.244)

whose Fourier transform is

(4.245)

If x₁(n) and x₂(n) are jointly SC with Loève bifrequency cross-spectrum (4.190a), the Loève bifrequency cross-spectrum of the expanded processes x_I1(n) and x_I2(n) (Figure 4.17) is given by

(4.246a)

(4.246b)

(4.246c)

where, in the third equality, the scaling property of the Dirac delta is used (Zemanian 1987, Section 1.7) and in the fourth equality (5.191) is accounted for. Equivalently, accounting for (4.190b), we also have

(4.247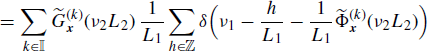a)

(4.247b)

(4.247c)

From (4.246a)–(4.246c) and (4.247a)–(4.247c) it follows that the expanded processes are jointly SC. In addition, their Loève bifrequency cross-spectrum is periodic in ν₁ with period 1/L₁ and in ν₂ with period 1/L₂.

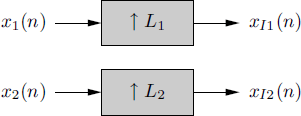
In the special case of x₁(n) and x₂(n) jointly ACS, accounting for (4.202), the Loève bifrequency cross-spectrum of the expanded processes x_I1(n) and x_I2(n) can be expressed as

(4.248a)

(4.248b)

(4.248c)

In (4.248a)–(4.248c), the cyclic spectra are periodic in ν₁ with period 1/L₁ and the delta train is periodic in ν₁ with period 1/L₁ and is periodic in ν₂ with period 1/L₂. Therefore, is periodic in ν₁ with period 1/L₁ and in ν₂ with period 1/L₂. In addition, from (4.248c) it follows that the Loève bifrequency cross-spectrum of the expanded processes x_I1(n) and x_I2(n) in the principal domain (ν₁, ν₂) [− 1/2, 1/2)² has support curves (for the case (−) present)

(4.249)

that is, lines with slope L₁/L₂. Consequently, x_I1(n) and x_I2(n) are jointly SC. In particular, for a single process x₁(n) ≡ x₂(n) ≡ x(n), by taking L₁ = 1, that is x_I1(n) ≡ x(n), it follows that the ACS process x(n) and its expanded version x_I2(n) are jointly SC with support lines with slope 1/L₂. In the special case of x(n) WSS, x(n) and x_I2(n) are jointly SC with support constituted by a unique line.

In Section 5.11 it is shown that when x₁(n) and x₂(n) are jointly ACS the cross-correlation function of x_I1(n) and x_I2(n) is given by

(4.250)

where the Kronecker delta is defined in (5.190) and is defined according to (4.244), that is,

(4.251)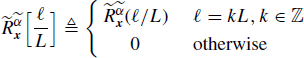

When L₁ ≠ L₂, the argument of the cyclic cross-correlation function contains the time variable n. Consequently, under the mild assumption that , it follows that, for every fixed m, the cross-correlation function in (4.250) as a function of n does not contain any finite-strength additive sinewave component. That is, x_I1(n) and do not exhibit joint almost-cyclostationarity at any cycle frequency:

(4.252)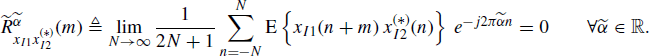

In particular, their time-averaged cross-correlation is identically zero. Moreover, from (4.250) it follows that x_I1(n) and x_I2(n) are jointly ACS if and only if L₁ = L₂ = L. In such a case, their cyclic cross-correlation functions are (Section 5.11)

(4.253)

Furthermore, since from (4.253) it follows

(4.254)

accordingly with the Fourier-transform pair (4.244) and (4.245), the cyclic cross-spectra of x_I1(n) and x_I2(n) are

(4.255)

In the special case of x₁ ≡ x₂, (4.253) and (4.255) reduce to (Izzo and Napolitano 1998b, eqs. (32) and (34)) specialized to second order.

4.10.2 Sampling

Let x_δi(n) be the sampled version of x_i(n), with sampling period M_i (i = 1, 2). That is

(4.256)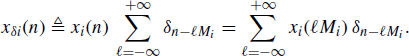

Accounting for (5.190), the Fourier transforms of the sampled processes are

(4.257)

where ⊗ denotes periodic convolution with period 1. Consequently, if x₁(n) and x₂(n) are jointly SC with with Loève bifrequency cross-spectrum (4.190a), then the Loève bifrequency cross-spectrum of x_δ1(n) and x_δ2(n) is

(4.258)

Equivalently, accounting for (4.190b) we also have

(4.259)

Thus, the sampled processes x_δ1(n) and x_δ2(n) are jointly SC. In addition, the Loève bifrequency cross-spectrum (4.258) (or (4.259)) is periodic in ν₁ with period 1/M₁ and in ν₂ with period 1/M₂.

In the special case where x₁(n) and x₂(n) are jointly ACS, accounting for (4.402), it results in

(4.260)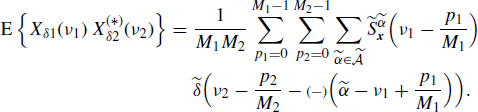

That is, the sampled processes are in turn jointly ACS for every value of M₁ and M₂. Such a result is not surprising since sampling is a linear periodically time-variant transformation (Napolitano 1995). In addition, if M₁ = M₂ = M, in Section 5.11 it is shown that the cyclic cross-correlation function of x_δ1(n) and x_δ2(n) is given by

(4.261)

By Fourier transforming both sides of (4.261) and using (5.190), we have the following expression for the cyclic cross-spectrum

(4.262)

where ⊗ denotes periodic convolution with period 1, and the fact that is the unit element for the periodic convolution with period 1 is used.

4.10.3 Decimation

4.10.3.1 LTV System Characterization

The M-fold decimated version x_D(n) of the discrete-time signal x(n), its link with the sampled signal x_δ(n), and the frequency-domain counterpart of these relationships are

(4.263)

(4.264)

(4.265)

(4.266)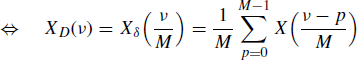

where (4.265) is obtained by (4.264) accounting for (4.239).

In Section 5.11 it is shown that decimation is a linear time-variant transformation (Figure 4.18)

(4.267)

with impulse-response function

(4.268)

and transmission function

(4.269a)

(4.269b)

(4.269c)

where and are defined in (4.243).

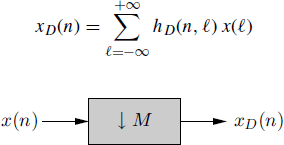
The function H_D(ν, λ) is periodic in ν with period 1 and periodic in λ with period 1/M. Systems performing M-fold decimation are a special case of discrete-time FOT-deterministic LTV systems (Section 4.3.1) not LAPTV.

4.10.3.2 Input/Output Statistics

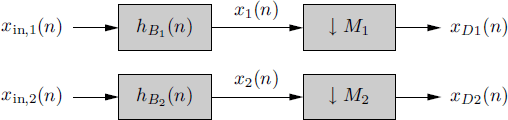
Let x_Di(n) be the decimated version of x_i(n), with decimation factor M_i (i = 1, 2) (Figure 4.19). That is,

(4.270)

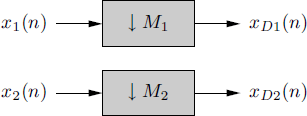
The cross-correlation functions of decimated, sampled, and original signals are linked by the relationship

(4.271)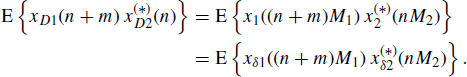

Since the sampled process is an expanded version of the decimated process, that is x_δi(n) = x_Di[n/M_i], accounting for (4.245), the Fourier transform of the sampled and decimated processes are linked by X_δi(ν) = X_Di(νM_i). Thus, using (4.257), the Fourier transforms of the decimated processes are

(4.272)

Therefore, if x₁(n) and x₂(n) are jointly SC with Loève bifrequency cross-spectrum (4.190a), by using (4.258) and (4.272), the Loève bifrequency cross-spectrum of x_D1(n) and x_D2(n) can be expressed as

(4.273a)

(4.273b)

(4.273c)

where, in the third equality, the scaling property of the Dirac delta (Zemanian 1987, Section 1.7) and identity (5.192) are used. Analogously, accounting for (4.259) one obtains the equivalent expressions

(4.274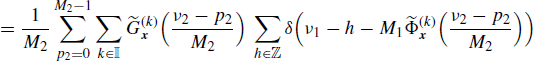a)

(4.274b)

(4.274c)

From (4.273a)–(4.273c) and (4.274a)–(4.274c) it follows that the decimated versions of jointly SC processes are jointly SC. In addition, unlike the case of sampled processes, their Loève bifrequency cross-spectrum is periodic with period 1 in both variables ν₁ and ν₂.

In the special case where x₁(n) and x₂(n) are jointly ACS, then accounting for (4.202) it results in

(4.275)

The cyclic spectra are periodic in ν₁ with period M₁ and the delta train is periodic in both ν₁ and ν₂ with period 1. In addition, from (4.275) it follows that the Loève bifrequency cross-spectrum of the decimated processes x_D1(n) and x_D2(n) in the principal domain (ν₁, ν₂) [− 1/2, 1/2)² has support curves (in the case (−) present)

(4.276)

that is, lines with slope M₂/M₁. Consequently, unlike the case of sampled processes, the decimated processes x_D1(n) and x_D2(n) are jointly SC. In particular, for a single process x₁(n) ≡ x₂(n) = x(n), by taking M₁ = 1, that is x_D1(n) ≡ x(n), it follows that the ACS process x(n) and its decimated version x_D2(n) are jointly SC with support lines with slope M₂. In the special case of x(n) WSS, the support line is unique.

In Section 5.11 it is shown that, when x₁(n) and x₂(n) are jointly ACS, the cross-correlation function of x_D1(n) and x_D2(n) is given by

(4.277)

By reasoning as for (4.250), we have that if then for M₁ ≠ M₂ the right-hand side of (4.277), as a function of n, does not contain any finite-strength additive sinewave component. That is, for M₁ ≠ M₂ the processes x_D1(n) and do not exhibit joint almost-cyclostationarity at any cycle frequency. From (4.275) and (4.277) it follows that x_D1(n) and x_D2(n) are jointly ACS if and only if M₁ = M₂ = M. In such a case, their cyclic cross-correlation function is (Section 5.11)

(4.278)

and, accounting for the Fourier-transform pair (4.270) and (4.272), their cyclic cross-spectrum can be expressed as

(4.279)

In the special case x₁ ≡ x₂, (4.278) and (4.279) reduce to (Izzo and Napolitano 1998b, eqs. (22) and (24)) specialized to second order. In addition, by comparing (4.261) with (4.278) the following relationship between cyclic cross-correlations of decimated and sampled signals can be established

(4.280)

or, equivalently

(4.281)

Moreover, by comparing (4.262) with (4.279) it results in

(4.282)

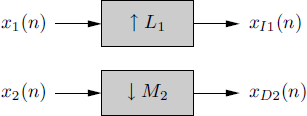
4.10.4 Expansion and Decimation

Let x_I1(n) and x_D2(n) be the L₁-fold expanded and M₂-fold decimated versions of x₁(n) and x₂(n), respectively (Figure 4.20).

If x₁(n) and x₂(n) are jointly SC processes with Loève bifrequency cross-spectrum (4.190a), accounting for (4.245) and (4.272) and using and (5.192), the Loève bifrequency cross-spectrum of x_I1(n) and x_D2(n) can be expressed as

(4.283a)

(4.283b)

(4.283c)

or equivalently, using (4.190a), as

(4.284a)

(4.284b)

(4.284c)

Thus x_I1(n) and x_I2(n) are jointly SC. In addition, from (4.283a)–(4.283c) and (4.284a)–(4.284c) it follows that their Loève bifrequency cross-spectrum is periodic in ν₁ with period 1/L₁ and in ν₂ with period 1.

If x₁(n) and x₂(n) are jointly ACS processes, (4.283c) specializes into

(4.285)

The cyclic spectra are periodic in ν₁ with period 1/L₁ and the delta train is periodic in ν₂ with period 1 and in ν₁ with period 1/(L₁M₂). Therefore, is periodic in ν₁ with period 1/L₁ and in ν₂ with period 1. In addition, from (4.285) it follows that x_I1(n) and x_D2(n) are jointly SC for every value of L₁ and M₂ except in the trivial case L₁ = M₂ = 1.

When x₁(n) and x₂(n) are jointly ACS, the cross-correlation function of x_L1(n) and x_D2(n) can be expressed as (Section 5.11)

(4.286)

Accordingly with the result in the frequency domain, the cross-correlation is an almost-periodic function of n for every fixed m if and only if L₁ = M₂ = 1. In such a case, x_L1(n) ≡ x₁(n) and x_D2(n) ≡ x₂(n) are jointly ACS. In contrast, if at least one of L₁ and M₂ is not unit, x_L1(n) and x_D2(n) are jointly SC. Under the mild assumption that , for every fixed m, the cross-correlation function in (4.286), as a function of n, does not contain any finite-strength additive sinewave component. That is, x_I1(n) and do not exhibit joint almost-cyclostationarity at any cycle frequency.

4.10.5 Strictly Band-Limited SC Processes

Let , with rect(ν) = 1 if |ν| ≤ 1/2 and rect(ν) = 0 otherwise, be the harmonic response of an ideal low-pass filter with monolateral bandwidth b < 1/2. A discrete-time nonstationary process x(n) is said to be strictly band-limited with bandwidth B if B is the smallest value of bandwidth b such that x(n) passes unaltered through a filter with harmonic response H_b(ν). In Section 4.9.1, the a.s. band-limitedness definition is given with reference to continuous-time processes. This definition can be extended with obvious changes to discrete-time processes.

Let x₁(n) and x₂(n) be jointly SC processes strictly band-limited with bandwidths B₁ and B₂, respectively. In Section 5.11 it is shown that for every term of the sum over in the Loève bifrequency cross-spectrum (4.190a) one has

(4.287a)

(4.287b)

where mod 1 is the modulo 1 operation with values in [− 1/2, 1/2). Analogously, starting from (4.190b), for every , one has

(4.288a)

(4.288b)

4.10.6 Interpolation Filters

Figure 4.21 presents two interpolation filters. Each interpolation filter (i = 1, 2) is constituted by a L_i-fold interpolator followed by a LTI filter with bandwidth W_i whose purpose is to obtain image-free interpolation (Crochiere and Rabiner 1981; Vaidyanathan 1990). An additional LTI filter with bandwidth B_i precedes the L_i-fold interpolator to strictly bandlimit the input process x_in,i(n) in order to avoid overlapping among images in the Loève bifrequency cross-spectrum.

In this section, the effects of interpolation filters on jointly SC processes are analyzed and sufficient conditions are established to assure that the Loève bifrequency cross-spectrum of the interpolated processes y₁(n) and y₂(n) is a frequency-scaled image-free version of that of the band-limited processes x₁(n) and x₂(n).

If x_in,1(n) and x_in,2(n) are jointly SC processes, then x₁(n) and x₂(n) are jointly SC processes strictly bandlimited with bandwidths B₁ and B₂, respectively (Section 4.3.2). Accounting for (4.246c), the Loève bifrequency cross-spectrum of y₁(n) and y₂(n) is given by

(4.289)

In Section 5.11 it is shown that

(4.290)

is a sufficient condition to assure that the Loève bifrequency cross-spectrum is a frequency-scaled image-free version of .

Condition (4.290) is independent of the shape of the support curves . In the special case of a single ACS process and L₁ = L₂ = L, is less restrictive than (Izzo and Napolitano 1998b, eq. (56)) specialized to second-order. In fact, (Izzo and Napolitano 1998b, eq. (56)) assures the lack of images in the densities of spectral correlation (the cyclic spectra) for ν₁ [− 1/(2L), 1/(2L)] and cycle frequencies . In Section 5.11, it is shown that

(4.291)

or, equivalently,

(4.292)

is a sufficient condition such that the density of Loève bifrequency cross-spectrum (4.289) along every support curve is a frequency-scaled image-free version of the corresponding density of Loève bifrequency cross-spectrum for every ν₁ [− 1/(2L₁), 1/(2L₁)]. Conditions (4.291) and (4.292) are independent of L₁ and L₂ and correspond to sufficient conditions to avoid aliasing in spectral cross-correlation densities in the case of sampling continuous-time SC processes (see (4.226) and (4.227)).

4.10.7 Decimation Filters

In Figure 4.22, two decimation filters are represented. Each decimation filter (i = 1, 2) is constituted by a M_i-fold decimator preceded by a LTI filter to strictly bandlimit the input process x_in,i(n) in order to avoid aliasing among replicas in the Loève bifrequency cross-spectrum. In this section, the effects of decimation filters on jointly SC processes are analyzed and sufficient conditions are established to assure that the Loève bifrequency cross-spectrum of the decimated processes x_D1(n) and x_D2(n) is a frequency-scaled alias-free version of that of the band-limited processes x₁(n) and x₂(n).

If x_in,1(n) and x_in,2(n) are jointly SC processes, then x₁(n) and x₂(n) are jointly SC processes strictly bandlimited with bandwidths B₁ and B₂, respectively (Section 4.3.2). The Loève bifrequency cross-spectrum of x_D1(n) and x_D2(n) is given by (4.273a)–(4.273c).

In Section 5.11 it is shown that

(4.293)

is a sufficient condition to assure that the Loève bifrequency cross-spectrum in (4.273a)–(4.273c) is a frequency-scaled alias-free version of .

Condition (4.293) is the Shannon condition to avoid aliasing in the sampled discrete-time processes. It is independent of the shape of the support curves . Moreover, in the special case of a single ACS process and M₁ = M₂, is less restrictive than (Izzo and Napolitano 1998b, eq. (40)) specialized to second-order. In fact, (Izzo and Napolitano 1998b, eq. (40)) assures the lack of aliasing replicas in the densities of spectral correlation (the cyclic spectra) for ν₁ [− 1/2, 1/2] and cycle frequencies .

In Section 5.11, it is shown that

(4.294)

or, equivalently,

(4.295)

is a sufficient condition such that the density of Loève bifrequency cross-spectrum (4.273a)–(4.273c) along every support curve is a frequency-scaled aliasing-free version of the corresponding density of Loève bifrequency cross-spectrum for every ν₁ [− 1/2, 1/2]. Conditions (4.294) and (4.295) are the discrete-time counterpart of sufficient conditions to avoid aliasing in spectral cross-correlation densities in the case of sampling continuous-time SC processes (see (4.226) and (4.227)).

4.10.8 Fractional Sampling Rate Converters

In Figure 4.23, two systems are represented, that perform sampling rate conversions by noninteger (rational) numbers M_i/L_i, (i = 1, 2). Each input process x_i(n) is assumed to be strictly band limited with bandwidth B_i. An ideal low-pass filter with bandwidth W_i follows the L_i-fold interpolator in order to cancel spectral images.

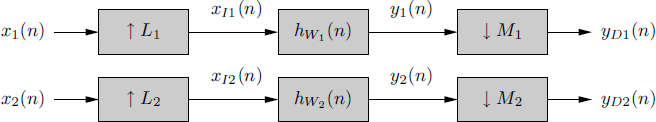
Let x₁(n) and x₂(n) be jointly SC processes with Loève bifrequency cross-spectrum (4.190a). In Section 5.11 it is shown that

(4.296)

Let x₁(n) and x₂(n) be strictly band limited with bandwidths B₁ and B₂, respectively. According to the results of Section 4.10.6, B_i/L_i ≤ W_i ≤ 1/(2L_i), (i = 1, 2), is a sufficient condition to assure that the Loève bifrequency cross-spectrum is a frequency-scaled image-free version of . In addition, since y₁(n) and y₂(n) are jointly SC with bandwidths W₁ and W₂, according to the results of Section 4.10.7, M_iW_i ≤ 1/2, (i = 1, 2), is a sufficient condition to assure that the Loève bifrequency cross-spectrum is a frequency-scaled aliasing-free version of . Therefore,

(4.297)

is a sufficient condition to assure that the Loève bifrequency cross-spectrum is a frequency-scaled image-and aliasing-free version of .