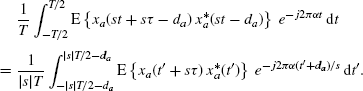7.10 Proofs

7.10.1 Proof of (7.262)

Fourier transform of a time-scaled, delayed, and frequency-shifted signal:

(7.383)

(7.384)

(7.385)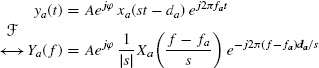

7.10.2 Proof of (7.263) and (7.264)

By using (7.261), the result is that

(7.386)

where is the continuous-time infinite average with respect to t, and, in the third equality, the variable change t′ = st − d_a is made, so that

(7.387)

This proof can be equivalently carried out in the FOT approach by simply removing the expectation operator E{ · } in (7.386) and (7.387).

(7.264) is obtained by Fourier transforming both sides of (7.263).

7.10.3 Proof of (7.262) and (7.272)

By reasoning as for (7.386), we have

(7.388)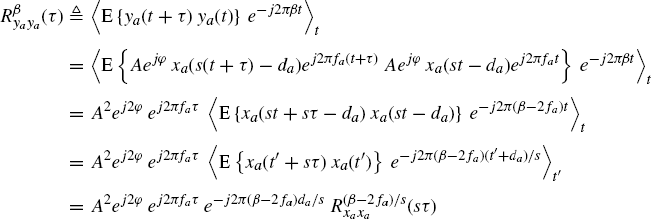

(7.268) is obtained by Fourier transforming both sides of (7.267).

7.10.4 Proof of (7.273)

Accounting for (7.262) and (7.272), one obtains

(7.389)

from which (7.273) follows by a variable change in the argument of the Dirac delta (Zemanian 1987, Section 1.7).

7.10.5 Proof of (7.275)

Using (7.261), we have

(7.390)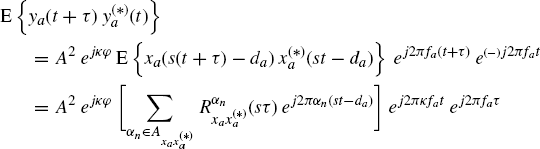

from which (7.275) immediately follows. The same result is obtained by taking the double inverse Fourier transform (see (1.15)) of both sides of (7.273) and then making the variable changes t₁ = t + τ, t₂ = t.

7.10.6 Proof of (7.276)

Accounting for (7.262), one obtains

(7.391)

from which (7.276) immediately follows using (7.272).

7.10.7 Proof of (7.286) and (7.287)

Accounting for (7.284) and (1.88), we have

(7.392)

where the last equality is obtained by putting and into (1.88).

Under assumption (1.89), . Thus, if for k₁ ≠ k₂, then each term in the sum over α in (7.392) is a finite-strength additive sinewave component of the cyclic autocorrelation function only when k₁ = k₂ = k so that there is no dependence on t in the argument of . Thus we have the first and second equality in (7.286).

By taking the Fourier coefficient at frequency β in (7.286) we have

(7.393)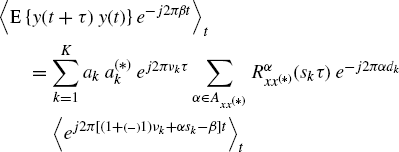

from which (7.287) easily follows observing that the last time average on t equals to the Kronecker delta .

Note that (7.287) can be obtained as special case of (Izzo and Napolitano 2002b, eq. (90)) for N = 2 with only the second optional complex conjugation present, by using (Izzo and Napolitano 1998a, eq. (36)) that expresses reduced-dimension (generalized) cyclic temporal moment functions in terms of (generalized) cyclic temporal moment functions.

7.10.8 Proof of Theorem 7.7.3 Doppler-Stretched Signal: Sampling Theorem for Loève Bifrequency Spectrum

Replicas in (7.325) are separated by 1 in both ν₁ and ν₂ variables. Thus, from (7.326a) it follows that f_s ≥ 2B|s| is a sufficient condition such that replicas do not overlap. Note that, even if replicas do not overlap, the mapping ν_i = f_i/f_s, i = 1, 2, does not link (7.273) and (7.325) for ν_i [− 1/2, 1/2]. A sufficient condition to assure such a mapping or, equivalently, that only replica (n₁, n₂) in (7.325) lies in the square (ν₁, ν₂) (n₁ − 1/2, n₁ + 1/2) × (n₂ − 1/2, n₂ + 1/2), according to (7.326b) is , that is, , where (7.298) is accounted for.

7.10.9 Proof of Theorem 7.7.4 Doppler Stretched Signal: Sampling Theorem for the Density of Loève Bifrequency Spectrum

According to (7.326a), if , the mapping ν₁ = f₁/f_s for ν₁ [− 1/2, 1/2] between the densities in (7.325) with n₁ = n₂ = 0 and those in (7.273) is assured provided that the support of replica with n₁ = n₂ = 0 does not intercept that of replicas with n₁ = 0, n₂ = ± 1. That is, on every support line

(7.394)

the following implication

(7.395)

must hold, where (7.394) is obtained by rearranging the argument of the Dirac delta in (7.325). From (7.394) with substituted into we have

(7.396)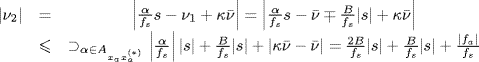

where the bound for comes form (1.176b). Thus, inequality in (7.95) is satisfied provided that that is, f_s ≥ 2(2B|s| + |f_a|).

These results agree with those in (Napolitano 2010b, Theorem 3) since (−)κ = κ.

7.10.10 Proof of Theorem 7.7.5 Doppler Stretched Signal: Sampling Theorem for the (Conjugate) Cyclic Spectrum

By setting and into the cyclic-spectrum support expression (1.176a), we have

(7.397)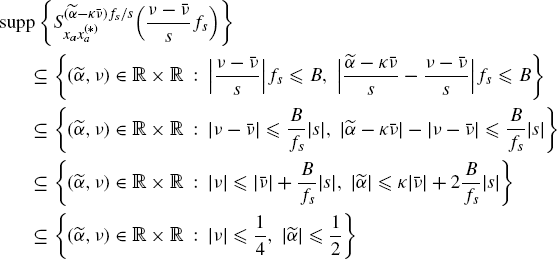

where the last inclusion relationship holds provided that inequality f_s ≥ȅ4(B|s| + |f_a|) is satisfied. In fact, accounting for (7.298), such an inequality is equivalent to .

Replicas in (7.329) are separated by 1 in both and ν domains. Consequently, condition f_s ≥ 4(B|s| + |f_a|) assures that only replica with p = 0 and q = 0 gives nonzero contribution in the principal domain . Then, observing that only replicas with p = q = 0 are coincident in (7.329) and (7.330), equation (7.331) immediately follows.

7.10.11 Proof of Theorem 7.7.6 Sampling Theorem for Loève Bifrequency Cross-Spectrum

Replicas in the aliasing formula (7.332) are separated by 1 in both ν₁ and ν₂ variables. Thus, from the support bound (7.333a) it follows that B|s|/f_s ≤ 1/2 and B/f_s ≤ 1/2 that is,

(7.398)

is a sufficient condition such that replicas do not overlap. Moreover, from (7.333b), it follows that a sufficient condition to obtain that only the replica (n₁, n₂) lies in the square (ν₁, ν₂) (n₁ − 1/2, n₁ + 1/2) × (n₂ − 1/2, n₂ + 1/2) is and B/f_s ≤ 1/2. Thus, accounting for (7.298), for the replica with n₁ = n₂ = 0 we have (7.334).

7.10.12 Proof of Theorem 7.7.7 Sampling Theorem for the Density of Loève Bifrequency Cross-Spectrum

Due to (7.333a), the mapping ν₁ = f₁/f_s1 for ν₁ [− 1/2, 1/2] between the densities with n₁ = n₂ = 0 in (7.332) and those in (7.276) is assured provided that the support replica with n₁ = n₂ = 0 does not intercept that of the replica with n₁ = 0, n₂ = ± 1. That is, on every support line

(7.399)

the following implication

(7.400)

must hold. From (7.399) with substituted into we have

(7.401)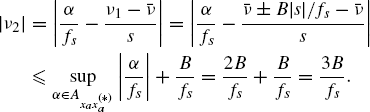

Thus, inequality in (7.400) is satisfied provided that 3B/f_s ≤ 1 − B/f_s, that is, f_s ≥ 4B. Then, accounting for (7.334), we obtain (7.336).

7.10.13 Proof of Theorem 7.7.8 Sampling Theorem for the (Conjugate) Cyclic Autocorrelation Function

From (7.339) (with y(n) = x_s(n), A = 1, ϕ = 0, , and d = 0) it follows that

(7.402)

Thus, if or if for |α| > f_s/2, then for the sum in the rhs of (7.339) equals the rhs of (7.402) and, hence, . A sufficient condition to assure for |α| > f_s/2 is that the bandwidth of x_as(t) is less than f_s/2 (Section 1.3.9), (Napolitano 1995; Gardner et al. 2006). That is, B|s| ≤ f_s/2, i.e., (7.340).