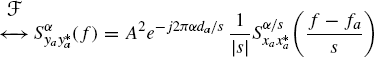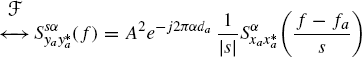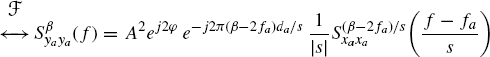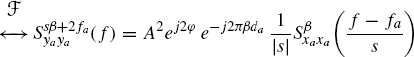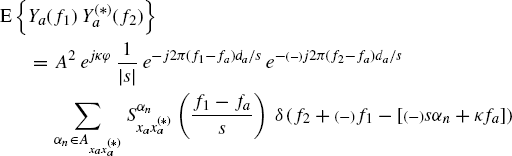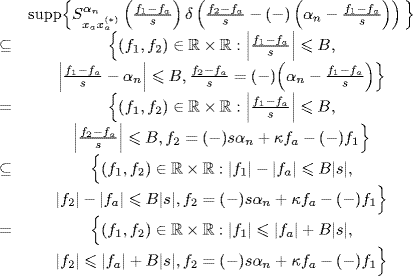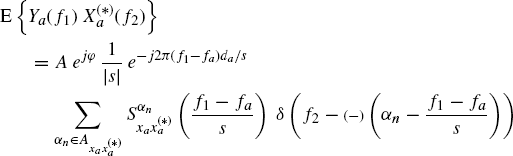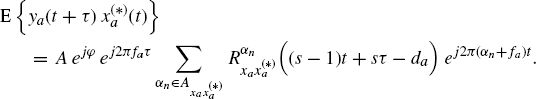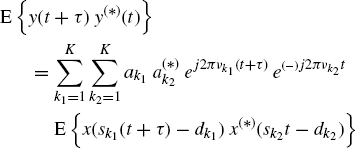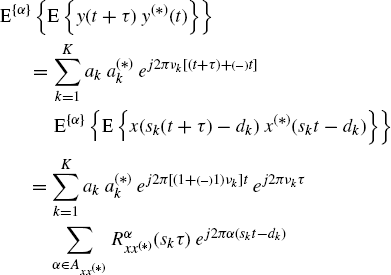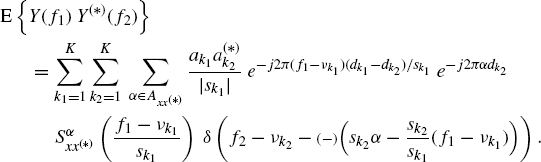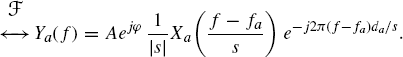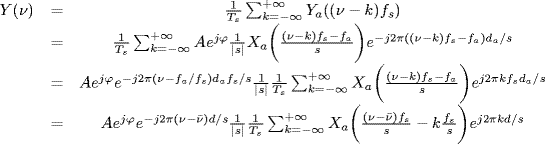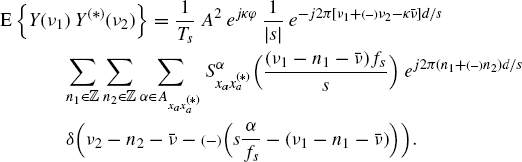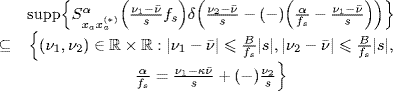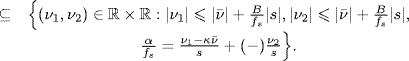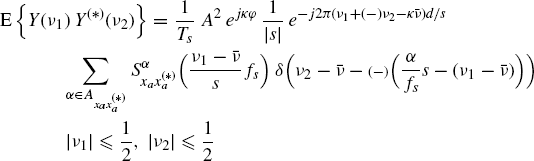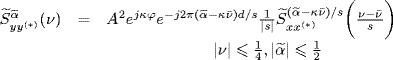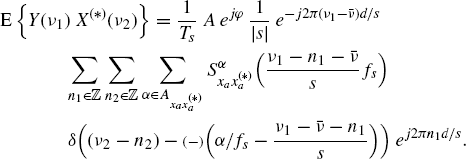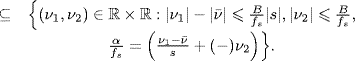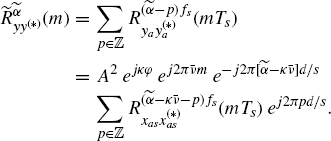7.7 Spectral Analysis of Doppler-Stretched Signals –Constant Radial Speed
In this section, the spectral analysis of the Doppler stretched signal received in the case of constant relative radial speed between TX and RX is addressed. The second-order statistical characterization is made in both time and frequency domains and both continuous-and discrete-time cases are considered. Sampling theorems are proved to obtain input/output relationships for discrete-time sampled signals which are formally analogous to their continuous-time counterparts. Proofs are reported in Section 7.10.
Let us consider the continuous-time Doppler-stretched signal (Section 7.3):
It is a time-scaled, delayed, and frequency-shifted version of the transmitted signal xa(t). Its Fourier transform is given by (Section 7.10)
7.7.1 Second-Order Statistics (Continuous-Time)
Let xa(t) exhibit (conjugate) cyclostationarity. Then, also ya(t) exhibits (conjugate) cyclostationarity and its cyclic statistics are linked to those of xa(t) as follows.
7.7.1.1 Cyclic Autocorrelation Function and Cyclic Spectrum
The cyclic autocorrelation function and the cyclic spectrum of ya(t) are given by (Section 7.10)
(7.263) ![]()
Equivalently,
Thus, if xa(t) exhibits cyclostationarity at cycle frequency αx, then ya(t) exhibits cyclostationarity at cycle frequency α = sαx.
7.7.1.2 Conjugate Cyclic Autocorrelation Function and Conjugate Cyclic Spectrum
The conjugate cyclic autocorrelation function and the conjugate cyclic spectrum of ya(t) are given by (Section 7.10)
Equivalently,
Thus, if xa(t) exhibits conjugate cyclostationarity at conjugate cycle frequency βx, then ya(t) exhibits conjugate cyclostationarity at conjugate cycle frequency β = sβx + 2fa.
Let xa(t) be ACS. Its (conjugate) autocorrelation function (1.88) and Loève bifrequency spectrum (1.94) are reported here for convenience:
In the following it is shown that for s ≠ 1, xa(t) and ya(t) are singularly but not jointly ACS. Specifically, xa(t) and ya(t) are jointly SC.
7.7.1.3 Loève Bifrequency Spectrum –ACS Input Signal
The Loève bifrequency spectrum of ya(t) is given by (Section 7.10)
where κ ![]() (1 + (−)1), that is, κ = 0 if (−) = − and κ = 2 if (−) = +. From (7.273), it follows that the Loève bifrequency spectrum of ya(t) has support contained in lines with slopes ±1. That is, the Doppler-stretched signal ya(t) is ACS. Moreover, its (conjugate) cyclic spectra can be related to those of the transmitted signal xa(t) by (7.264), (7.266)(7.268), and (7.270). Therefore, due to the Doppler channel, cycle frequencies of xa are scaled by s and conjugate cycle frequencies of xa are scaled by s and shifted by 2fa.
(1 + (−)1), that is, κ = 0 if (−) = − and κ = 2 if (−) = +. From (7.273), it follows that the Loève bifrequency spectrum of ya(t) has support contained in lines with slopes ±1. That is, the Doppler-stretched signal ya(t) is ACS. Moreover, its (conjugate) cyclic spectra can be related to those of the transmitted signal xa(t) by (7.264), (7.266)(7.268), and (7.270). Therefore, due to the Doppler channel, cycle frequencies of xa are scaled by s and conjugate cycle frequencies of xa are scaled by s and shifted by 2fa.
Accounting for (1.178a) and (1.178b), the support of the generic term of the sum over α in (7.389) (which is equivalent to (7.273)) is such that
Note that the ACS nature of ya(t) is not an obvious result. In fact, relation (7.261) describes a transformation of the input signal xa(t) into the output signal ya(t) which is linear time-variant but not almost-periodically time-variant. Only in this last case it is known that ACS signals are transformed into ACS signals (Section 1.3.3), (Napolitano 1995), (Gardner et al. 2006). Transformation described by (7.261) is a special case of deterministic transformation in the FOT probability sense (Section 4.3.1), (Izzo and Napolitano 2002a, 2005).
7.7.1.4 (Conjugate) Autocorrelation Function –ACS Input Signal
In Section 7.10, it is shown that for an input ACS signal the (conjugate) autocorrelation function of the signal ya(t) in (7.261) is given by
which agrees with (7.265) and (7.269) derived in the more general case of xa(t) that exhibits cyclostationarity.
7.7.1.5 Loève Bifrequency Cross-Spectrum –ACS Input Signal
The Loève bifrequency cross-spectrum of ya(t) and xa(t) is given by (Section 7.10)
Thus, when s ≠ 1, the Loève bifrequency cross-spectrum has support contained in lines with slopes different from ±1. That is, even if both signals xa(t) and ya(t) are (singularly) ACS, they are not jointly ACS. The joint nonstationary behavior of xa(t) and ya(t) can be described resorting to the class of the SC signals. In fact, jointly SC signals have Loève bifrequency cross-spectrum with spectral masses concentrated on a countable set of curves in the bifrequency plane. From (7.276) it follows that ya(t) and xa(t) are jointly SC with support curves constituted by lines with slopes ±1/s. Specifically, with reference to the notation introduced in Chapter 4, we have
(7.277) ![]()
with
(7.278) ![]()
(7.279) ![]()
(7.280) ![]()
Assuming the transmitted signal xa(t) strictly band-limited with bandwidth B, and accounting for (1.178a) and (1.178b), the support of the generic term of the sum over α in (7.276) is such that
(7.281) 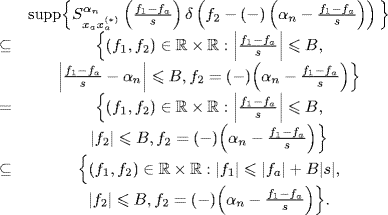
7.7.1.6 Cross-Correlation Function –ACS Input Signal
By using (7.261) and (7.271) leads to
(7.282) 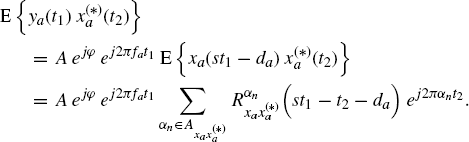
Moreover, by the variable change t1 = t + τ, t2 = t we have
Thus, under the mild assumption that ![]() , ∀αn, the function of t in the rhs of (7.283) can contain finite-strength additive sinewave components if and only if s = 1, i.e., if there is no dependence on t in the argument of
, ∀αn, the function of t in the rhs of (7.283) can contain finite-strength additive sinewave components if and only if s = 1, i.e., if there is no dependence on t in the argument of ![]() . That is, according to the frequency-domain result, for s ≠ 1 the cross-correlation function
. That is, according to the frequency-domain result, for s ≠ 1 the cross-correlation function ![]() is not an almost-periodic function of t, that is, ya(t) and xa(t) are not jointly ACS.
is not an almost-periodic function of t, that is, ya(t) and xa(t) are not jointly ACS.
7.7.2 Multipath Doppler Channel
In Section 7.6.1, it is shown that the output signal y(t) of a multipath Doppler channel introducing complex gain, time-scale factor, delay, and frequency shift for each path, for input signal x(t) is
7.7.2.1 Output Statistics
From (7.284), it follows that the (conjugate) autocorrelation function of y(t) is
In Section 7.10 it is shown that for an ACS input signal x(t), under the mild assumption of (conjugate) cyclic autocorrelation function summability (1.89), if ![]() for k1 ≠ k2, then the almost-periodic component of the (conjugate) autocorrelation function is given by
for k1 ≠ k2, then the almost-periodic component of the (conjugate) autocorrelation function is given by
In addition, the (conjugate) cyclic autocorrelation function of the output signal y(t) is
In contrast, if the length T of the observation interval is such that the narrow-band condition (see (7.222) and (7.223))
holds for all paths, then ![]() and
and ![]() can be assumed in (7.285) and the multipath Doppler channel is LAPTV. Thus, it transforms ACS input signals into ACS output signals. Consequently, for an ACS input signal x(t), the (conjugate) autocorrelation function of the output signal y(t) is coincident with its almost-periodic component and, accounting for (c07-mdis-0412) with
can be assumed in (7.285) and the multipath Doppler channel is LAPTV. Thus, it transforms ACS input signals into ACS output signals. Consequently, for an ACS input signal x(t), the (conjugate) autocorrelation function of the output signal y(t) is coincident with its almost-periodic component and, accounting for (c07-mdis-0412) with ![]() , the result is
, the result is
and
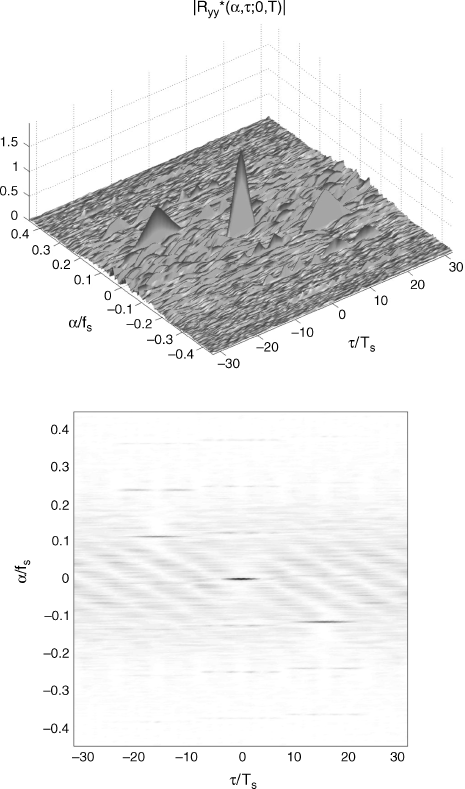
To corroborate the result that a different behavior of the cyclic autocorrelation function is predicted by (7.287) or (7.290) depending on the data-record length adopted for the cyclic correlogram estimate, the following experiment is carried out. A binary PAM signal with bit rate 1/8Ts and full-duty-cycle rectangular pulse excites a multipath Doppler channel characterized by a1 = 1, d1 = 0, ν1 = 0.015/Ts, s1 = 1.001, a2 = 0.9, d2 = 15Ts, ν2 = − 0.1/Ts, and s2 = 0.999. In Figures 7.7 and 7.8, (top) graph and (bottom) “checkerboard” plot of the magnitude of the cyclic correlogram as a function of αTs and τ/Ts, estimated by a data-record length of 215 samples and 210 samples, respectively, are reported. For T = 215Ts one has BT ![]() 4096 and 1/|1 − sk| = 1000, k = 1, 2. Thus, the narrow-band condition (7.288) is not satisfied and (7.287) describes the cyclic autocorrelation function of the output (Figure 7.7). In contrast, for T = 210Ts one has BT
4096 and 1/|1 − sk| = 1000, k = 1, 2. Thus, the narrow-band condition (7.288) is not satisfied and (7.287) describes the cyclic autocorrelation function of the output (Figure 7.7). In contrast, for T = 210Ts one has BT ![]() 128 and 1/|1 − sk| = 1000, k = 1, 2, and the narrow-band condition (7.288) holds. Therefore, (7.290) describes the cyclic autocorrelation function of the output. Also terms with k1 ≠ k2 give nonzero contribution (Figure 7.8).
128 and 1/|1 − sk| = 1000, k = 1, 2, and the narrow-band condition (7.288) holds. Therefore, (7.290) describes the cyclic autocorrelation function of the output. Also terms with k1 ≠ k2 give nonzero contribution (Figure 7.8).
Figure 7.7 Output signal of a multipath Doppler channel excited by a PAM input signal. (Top) graph and (bottom) “checkerboard” plot of the magnitude of the cyclic correlogram as a function of αTs and τ/Ts, estimated by a data-record length of 215 samples (narrow-band condition (7.288) not satisfied)
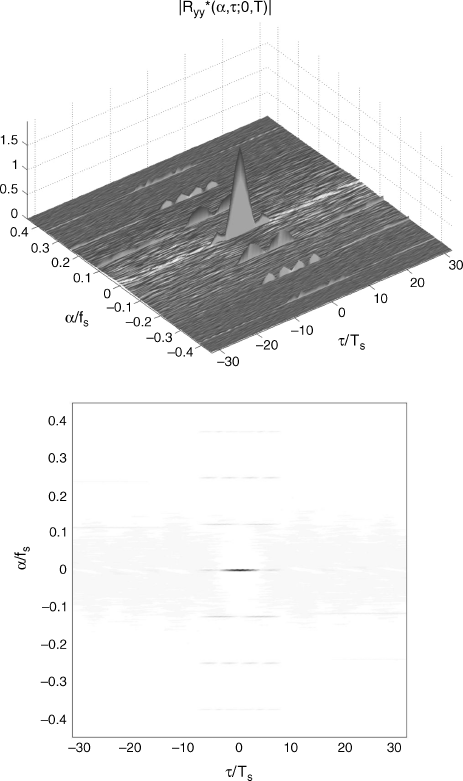
Figure 7.8 Output signal of a multipath Doppler channel excited by a PAM input signal. (Top) graph and (bottom) “checkerboard” plot of the magnitude of the cyclic correlogram as a function of αTs and τ/Ts, estimated by a data-record length of 210 samples (narrow-band condition (7.288) satisfied)
Briefly, both the above analysis and previous experiment show that if the product bandwidth data-record length is sufficiently small, then the multipath Doppler channel can be modeled as a LAPTV system since the effects of the time scaling factors can be ignored in the argument of the complex envelope of the received signal. In contrast, if the data-record length is increased (e.g., to obtain high noise immunity in cyclostationarity-based algorithms), the time-scaling factors must be taken into account, and the system cannot be modeled as LAPTV but, rather, as FOT deterministic.
Equations (7.285), (7.286), (7.287), (7.289), and (7.290) can also be written in the functional approach by substituting the statistical expectation operator with the almost-periodic component extraction operator E{α}{ · } (Izzo and Napolitano 2002b), (Izzo and Napolitano 2005) and observing that E{α}{E{α}{ · }} ≡ E{α}{ · }. In such a case, however, equalities must be intended in the temporal mean-square sense (Section 6.3.5, (Gardner et al. 2006, Section 4.2), (Izzo and Napolitano 2005, Appendix A)). Alternatively, almost periodicity should be considered in some of the generalized senses addressed in Sections 1.2.2, 1.2.3, 1.2.4, 1.2.5 (see also (Besicovitch 1932, Chapter 2), (Bohr 1933, paragraphs 94–102), (Corduneanu 1989, Chapter VI)).
Accounting for (7.262), we have the following expression for the Loève bifrequency spectrum of y(t)
(7.291) 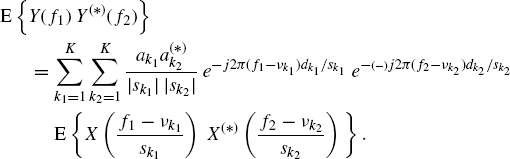
which, in the special case of ACS input signal, accounting for (7.273), reduces to
Equation (7.292) shows that for an input ACS signal, the Loève bifrequency spectrum of the output signal has support contained in lines with slopes ![]() . Thus, the output signal is SC provided that at least two time-scale factors are different.
. Thus, the output signal is SC provided that at least two time-scale factors are different.
7.7.2.2. Input/Output Cross-Statistics
Accounting for (7.276), the Loève bifrequency cross-spectrum of y(t) and x(t) is given by
(7.293) 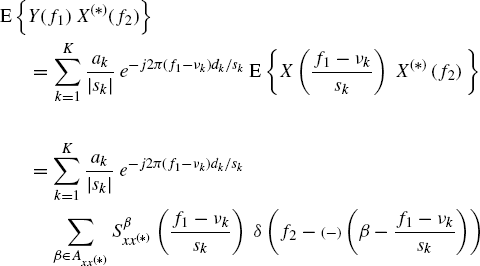
That is, the input and output signals of the multipath Doppler channel are jointly SC signals.
7.7.3 Doppler-Stretched Signal (Discrete-Time)
In this section, the equivalent discrete-time Doppler channel obtained by uniformly sampling input and output signals of a continuous-time Doppler channel is considered. Input/output relationships in both time and frequency domains are derived. Moreover, a sampling theorem is proved such that the input/output relationship in the frequency domain is formally equivalent to its continuous-time counterpart.
In the case of constant relative radial speed between TX and RX (Section 7.3) the continuous-time Doppler-stretched received signal and its Fourier transform are given by (7.261) and (7.262), respectively, reported here for convenience
(7.294) ![]()
Let us consider the uniformly sampled discrete-time signal
(7.296) ![]()
where Ts = 1/fs is the sampling period and let us define
(7.297) ![]()
(7.299) ![]()
where ![]() is the normalized frequency shift and d is the (possibly non-integer) normalized delay.
is the normalized frequency shift and d is the (possibly non-integer) normalized delay.
Accounting for the relationship (5.184) between the Fourier transform of a continuous-time signal and that of its uniformly sampled version
the Fourier transform of the discrete-time signal y(n) is given by
The following remarks are in order.
From the above remarks we find that a discrete-time counterpart of (7.295) formally analogous to (7.295) cannot be straightforwardly derived from (7.301).
Let xa(t) be strictly band-limited, that is, Xa(f) = 0 for |f| > B. Thus,
(7.303) ![]()
With the mapping f = νfs, replicas in (7.301) are centered in multiples of fs. Hence, a sufficient condition to avoid replicas' overlap in (7.301) is fa + |s|B ≤ fa + fs − |s|B (Figure 7.9), that is
Note that the frequency shift fa has no influence in this condition. A sufficient condition to obtain that only the kth replica has support contained in the interval
is (Figure 7.9)
In such a case, the frequency shift fa has influence and condition (7.306) is more restrictive than condition (7.304) that only avoids replicas' overlap.
Figure 7.9 Sampled stretched spectra (fa > 0, |s| > 1, s ![]() 0)
0)
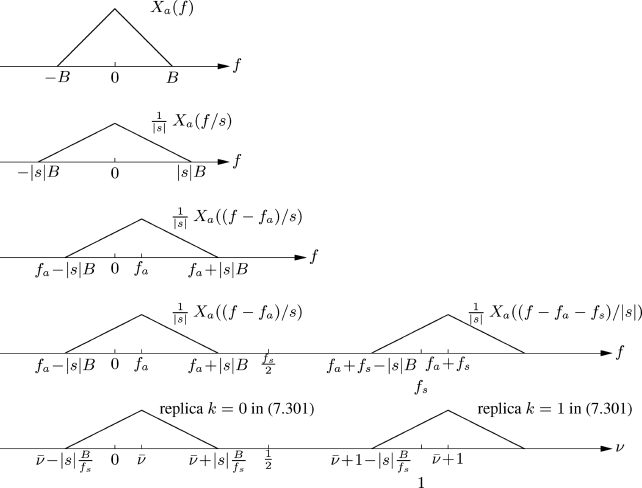
Conditions (7.304) and (7.306) can be written in terms of frequency ν accounting for the mapping ν = f/fs. Specifically (see Figure 7.9), condition (7.304) of replicas' non-overlap becomes
(7.307) ![]()
and condition (7.306) assuring that only the kth replica falls in the interval Ik becomes
(7.308) ![]()
Assumption 7.7.1 No Aliasing for the Discrete-Time Doppler Stretched Signal
(7.309) ![]()
Theorem 7.7.2 Sampling Theorem for Doppler-Stretched Signals. Under Assumption 7.7.1, it results that
which is formally analogous to its continuous-time counterpart (7.295).
Proof: By comparing replicas for k = 0 in (7.301) and (7.302), we obtain (7.311), provided that only replica for k = 0 in (7.301) is contained in the interval [−1/2,1/2) (that is, I0/fs, where I0 is defined according to (7.305)). ![]()
In the special case s = 1, (7.301) becomes
(7.312) ![]()
from which it follows
Equality in (7.313) holds ![]() only if
only if ![]() .
.
7.7.4 Simulation of Discrete-Time Doppler-Stretched Signals
In this section, an interpolation procedure is outlined to generate samples of a discrete-time Doppler-stretched signal. The method is extended to the generation of samples of time-warped version of a given signal with generic time-warping function. Then, its frequency-domain counterpart is considered to generate a frequency-warped version of a given signal.
Let xa(t) be strictly bandlimited, i.e., Xa(f) = 0 |f| > B and let fs ≥ 2B (sufficient condition assuring the replicas in (7.300) do not overlap). The following Shannon interpolation formula holds
(7.314) ![]()
where ![]() . In addition, if fs ≥ 2B|s| we also have
. In addition, if fs ≥ 2B|s| we also have
(7.315) ![]()
The more stringent condition (7.310) has to be verified to have that Theorem 7.7.2 holds. Thus, from (7.261) it follows that samples of the sequence y(n) can be generated by the following interpolation formula (see also (Chan and Ho 2005))
(7.316) 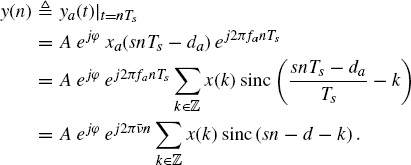
Analogously, a time-warped version of xa(t) say
(7.317) ![]()
where ψ(t) is the real-valued time-warping function, can be expressed as
(7.318) ![]()
provided that fs ≥ 2B′, with B′ the monolateral bandwidth of xa(ψ(t)). Consequently, samples of ya(t) can be generated by the interpolation formula
(7.319) ![]()
In particular, this relation can be used with ψ(t) = t − D(t) in the case of constant relative radial acceleration with D(t) given by (7.201).
The problem of the bandlimitedness of time-warped versions of bandlimited signals is addressed in (Cochran and Clark 1990), (Xia and Zhang 1992), (Clark and Cochran 1993), (Azizi and Cochran 1999), (Azizi et al. 2002). In particular, in (Xia and Zhang 1992) it is shown that if xa(t) is strictly band-limited, within a large class of time-warping functions, the time-warped signal ya(t) = xa(ψ(t)) is strictly band-limited if and only if ψ(t) is affine, i.e., ψ(t) = st − d. Consequently, for a generic time-warping function ψ(t), even if xa(t) is strictly band-limited, in general ya(t) can only be approximatively band-limited.
A similar interpolation procedure can be adopted to generate samples of a frequency-warped version of x(n). Let X(k/N) be the DFT of the finite N-length sequence x(n) defined for n ![]() {0, 1, …, N − 1} (see (3.215)). The Fourier transform of x(n) can be expressed by the interpolation formula
{0, 1, …, N − 1} (see (3.215)). The Fourier transform of x(n) can be expressed by the interpolation formula
(7.320) ![]()
where ![]() is the Dirichlet kernel defined in (3.216b). Thus, for a generic real-valued frequency-warping function Ψ(ν) (with −1/2 ≤ Ψ(ν) ≤ 1/2) we have that the frequency-warped version of x(n) has Fourier transform
is the Dirichlet kernel defined in (3.216b). Thus, for a generic real-valued frequency-warping function Ψ(ν) (with −1/2 ≤ Ψ(ν) ≤ 1/2) we have that the frequency-warped version of x(n) has Fourier transform
(7.321) ![]()
and DFT
(7.322) ![]()
The samples y(n) of the frequency-warped version of x(n) are obtained by inverse discrete Fourier transform (IDFT) of the sequence Yk
(7.323) ![]()
7.7.5 Second-Order Statistics (Discrete-Time)
In this section, sampling theorems are proved for the statistical functions characterizing the uniformly sampled Doppler-stretched received signal and jointly characterizing the sampled transmitted and received signals. In addition, sufficient conditions are derived to avoid aliasing in the relationships linking spectral functions of sampled transmitted and received signals in order to make these relationships formally analogous to their continuous-time counterparts (7.264), (7.268), (7.273), and (7.276) which are obtained starting from the continuous-time physical model (7.261)–(7.262) for the propagation channel. This formal analogy allows, for example, straightforward discrete-time implementations of the Doppler-channel parameter estimation algorithm proposed in continuous-time in (De Angelis et al. 2005), and the range-Doppler estimation algorithms proposed in (Napolitano and Do![]() ançay 2011).
ançay 2011).
Analogous results could be obtained by specializing results of Section 4.9.2 to the case of support curves which are lines. In this section, however, by exploiting the linearity of the support curves, less stringent constraints on the sampling frequency fs are obtained with respect to those that can be obtained specializing the results of Section 4.9.2.
In the following, for convenience, equations (7.264) and (7.268) will be expressed by the unique equation
where κ ![]() (1 + (−)1), that is, κ = 0 if (−) = − and κ = 2 if (−) = +.
(1 + (−)1), that is, κ = 0 if (−) = − and κ = 2 if (−) = +.
Accounting for the Fourier transform (7.262) of the Doppler-stretched signal, the Loève bifrequency spectrum (7.272) of ACS signals, and the Fourier transform (7.300) of sampled signals, the following aliasing formula for the Loève bifrequency spectrum of y(n) is obtained when xa(t) is an ACS signal:
The discrete-time signal y(n) is ACS since its Loève bifrequency spectrum has support contained in lines with slope ±1 in the bifrequency plane (ν1, ν2). In addition, if xa(t) is band-limited with bandwidth B, accounting for (1.178b), the support of the replica with n1 = n2 = 0 in the aliasing formula (7.325) is a frequency scaled version of that in (7.274) and is reported here for future reference
Starting from (7.325)–(7.326b), the following results can be proved, which provide sufficient conditions to avoid aliasing in the Loève bifrequency spectrum of y(n) and its density.
Theorem 7.7.3 Doppler-Stretched Signal: Sampling Theorem for Loève Bifrequency Spectrum (Napolitano 2010b, Theorem 2). Let xa(t) be ACS and band-limited with bandwidth B. For fs ≥ 2B|s| replicas in the aliasing formula (7.325) do not overlap. Furthermore, for fs ≥ 2(B|s| + |fa|) one obtains
which is coincident with its continuous-time counterpart (7.273) but for the amplitude scale factor 1/Ts and the scaling factor fs in both frequency variables.
Proof: See Section 7.10. ![]()
An application of Theorem 7.7.3 is illustrated in Section 7.7.6 (Figures 7.10, 7.11, and 7.12).
Figure 7.10 (Continuous-time) Doppler-stretched signal ![]() , where xa(t) is a PAM signal with raised cosine pulse. (Top) magnitude and (bottom) support of the bifrequency spectral correlation density of ya(t), as a function of f1/fr and f2/fr.
, where xa(t) is a PAM signal with raised cosine pulse. (Top) magnitude and (bottom) support of the bifrequency spectral correlation density of ya(t), as a function of f1/fr and f2/fr.
Source: (Napolitano 2010b).

Figure 7.11 (Continuous-time) Doppler-stretched signal ![]() , where xa(t) is a PAM signal with raised cosine pulse. Bifrequency spectral correlation density of the discrete-time signal
, where xa(t) is a PAM signal with raised cosine pulse. Bifrequency spectral correlation density of the discrete-time signal ![]() , as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 2|s|B′.
, as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 2|s|B′.
Source: (Napolitano 2010b) Copyright of Elsevier
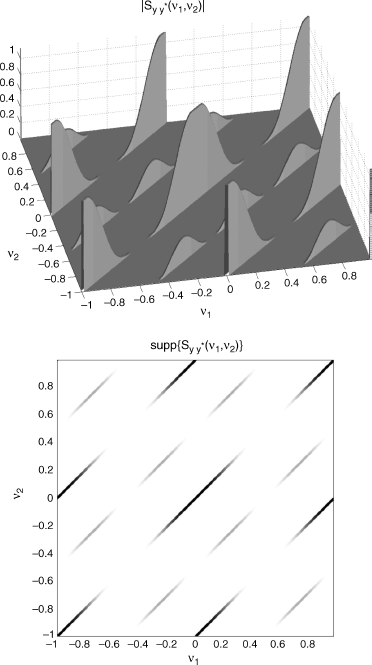
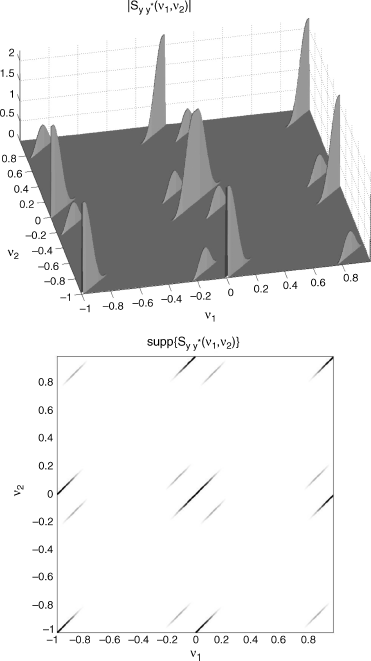
Figure 7.12 (Continuous-time) Doppler-stretched signal ![]() , where xa(t) is a PAM signal with raised cosine pulse. Bifrequency spectral correlation density of the discrete-time signal
, where xa(t) is a PAM signal with raised cosine pulse. Bifrequency spectral correlation density of the discrete-time signal ![]() , as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 4|s|B′.
, as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 4|s|B′.
Source: (Napolitano 2010b) Copyright of Elsevier.
Theorem 7.7.4 Doppler Stretched Signal: Sampling Theorem for the Density of Loève Bifrequency Spectrum (Napolitano 2010b, Theorem 3). Let xa(t) be ACS and band-limited with bandwidth B. For fs ≥ 2(2B|s| + |fa|), the density of Loève bifrequency spectrum of y(n) is given by
where k is an index in one-to-one correspondence with ![]() . In (7.328), for (−) = − one has ν1 − ν2 = αs/fs and for (−) = + one has
. In (7.328), for (−) = − one has ν1 − ν2 = αs/fs and for (−) = + one has ![]() .
.
Proof: See Section 7.10. ![]()
The sufficient condition on the sampling frequency in Theorem 7.7.4 can be made more stringent by requiring that not only the mapping between spectral frequencies ν1 = f1/fs holds for ν1 ![]() [− 1/2, 1/2] but also that the mapping between cycle frequencies
[− 1/2, 1/2] but also that the mapping between cycle frequencies ![]() holds for
holds for ![]() . This new condition assures the formal analogy between formulas in terms of cyclic spectra for continuous-and discrete-time cases. It can be obtained starting from the aliasing formula for the discrete-time (conjugate) cyclic spectrum of y(n) which can be derived accounting for (7.324) and (1.175):
. This new condition assures the formal analogy between formulas in terms of cyclic spectra for continuous-and discrete-time cases. It can be obtained starting from the aliasing formula for the discrete-time (conjugate) cyclic spectrum of y(n) which can be derived accounting for (7.324) and (1.175):
It is worth observing that the formal analogy between cyclic spectra of the discrete-time sampled signals and their continuous-time counterparts is not straightforward and should be carefully stated, as clarified by the following consideration. By replacing ![]() with
with ![]() and ν with
and ν with ![]() into the aliasing formula for cyclic spectra (1.175), it follows that
into the aliasing formula for cyclic spectra (1.175), it follows that
Even if the function in the left-hand-side (lhs) of (7.330) can be seen as the discrete-time counterpart of the cyclic spectrum in the right-hand-sides (rhs) of (7.324), both functions in the rhs and lhs of (7.330) are periodic in ν and ![]() with period s and, hence, are not (conjugate) cyclic spectra of discrete-time signals. The discrete-time counterpart of (7.324) is obtained by the following result.
with period s and, hence, are not (conjugate) cyclic spectra of discrete-time signals. The discrete-time counterpart of (7.324) is obtained by the following result.
Theorem 7.7.5 Doppler Stretched Signal: Sampling Theorem for the (Conjugate) Cyclic Spectrum (Napolitano 2010b, Theorem 4). Let xa(t) be ACS and band-limited with bandwidth B. For fs ≥ 4(B|s| + |fa|) one has
which is formally analogous to its continuous-time counterpart (7.324).
Proof: See Section 7.10. ![]()
An application of Theorems 7.7.5 and 7.7.6 is illustrated in Section 7.7.6 (Figure 7.13).
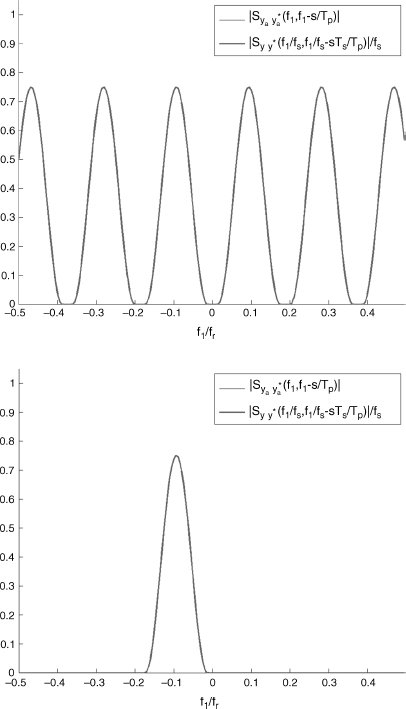
Figure 7.13 (Continuous-time) Doppler-stretched signal ![]() , where xa(t) is a PAM signal with raised cosine pulse. Slice of the magnitude of the spectral correlation density of the continuous-time signal ya(t) along the support line f2 = f1 − s/Tp (thin line) and of the rescaled (ν1 = f1/fs) spectral correlation density of the discrete-time signal
, where xa(t) is a PAM signal with raised cosine pulse. Slice of the magnitude of the spectral correlation density of the continuous-time signal ya(t) along the support line f2 = f1 − s/Tp (thin line) and of the rescaled (ν1 = f1/fs) spectral correlation density of the discrete-time signal ![]() , along ν2 = ν1 − s(Ts/Tp) (thick line) as a function of f1/fr. (Top) fs = 2|s|B′ [fs/2 = 0.1875fr] and (bottom) fs = 4|s|B′ [fs/2 = fr/2].
, along ν2 = ν1 − s(Ts/Tp) (thick line) as a function of f1/fr. (Top) fs = 2|s|B′ [fs/2 = 0.1875fr] and (bottom) fs = 4|s|B′ [fs/2 = fr/2].
Source: (Napolitano 2010b) Copyright of Elsevier
The spectral cross-characterization of y(n) and x(n) requires to prove sampling theorems in the case of signals that are not jointly ACS but, rather, jointly SC. Therefore, results for auto-statistics cannot be extended to cross-statistics.
Accounting for the Fourier transform (7.262) of the Doppler-stretched signal, the Loève bifrequency spectrum (7.272) of ACS signals, and the Fourier transform (7.300) of sampled signals, the following aliasing formula for the Loève bifrequency cross-spectrum of y(n) and x(n) can be derived when xa(t) is ACS:
From (7.332), it follows that the discrete-time signals x(n) and y(n) are jointly SC with the Loève bifrequency cross-spectrum having support contained in lines with slope ±1/s in the bifrequency plane (ν1, ν2).
If xa(t) is band-limited with bandwidth B, accounting for (1.178b), the support of the replica with n1 = n2 = 0 and fixed α in the aliasing formula (7.332) is such that
Equations (7.333a) and (7.333b) allow to establish the following results.
Theorem 7.7.6 Sampling Theorem for Loève Bifrequency Cross-Spectrum (Napolitano 2010b, Theorem 5). Let xa(t) be ACS and band-limited with bandwidth B. For
one obtains
(7.335) 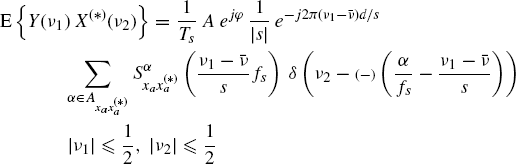
which is formally analogous to its continuous-time counterpart (7.276).
Proof: See Section 7.10. ![]()
An application of Theorem 7.7.6 is illustrated in Section 7.7.6 (Figures 7.14, 7.15, and 7.16).
Figure 7.14 (Continuous-time) PAM signal xa(t) with raised cosine pulse. (Top) magnitude and (bottom) support of the bifrequency spectral cross-correlation density of ![]() and xa(t), as a function of f1/fr and f2/fr.
and xa(t), as a function of f1/fr and f2/fr.
Source: (Napolitano 2010b) Copyright of Elsevier
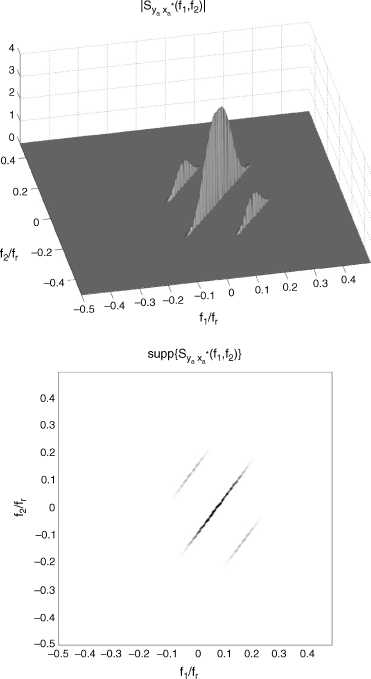
Figure 7.15 (Continuous-time) PAM signal xa(t) with raised cosine pulse and its Doppler-stretched version ![]() . Bifrequency spectral cross-correlation density of the discrete-time signals
. Bifrequency spectral cross-correlation density of the discrete-time signals ![]() and
and ![]() , as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 2B′.
, as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 2B′.
Source: (Napolitano 2010b) Copyright of Elsevier
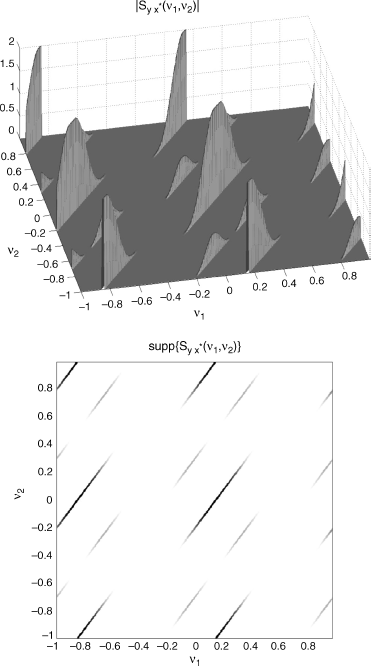
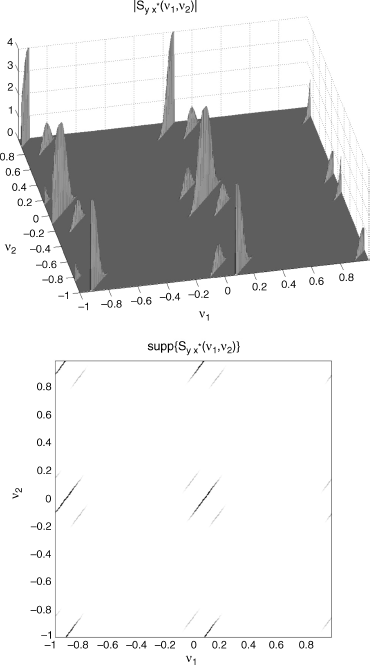
Figure 7.16 (Continuous-time) PAM signal xa(t) with raised cosine pulse and its Doppler-stretched version ![]() . Bifrequency spectral cross-correlation density of the discrete-time signals
. Bifrequency spectral cross-correlation density of the discrete-time signals ![]() and
and ![]() , as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 4B′.
, as a function of ν1 and ν2. (Top) magnitude and (bottom) support for fs = 4B′.
Source: (Napolitano 2010b) Copyright of Elsevier
Theorem 7.7.7 Sampling Theorem for the Density of Loève Bifrequency Cross-Spectrum (Napolitano 2010b, Theorem 6). Let xa(t) be ACS and band-limited with bandwidth B. For
one obtains that the density of the Loève bifrequency cross-spectrum (7.332) along the support line ![]() is given by
is given by
(7.337) ![]()
where k is an index in one-to-one correspondence with ![]() .
.
Proof: See Section 7.10. ![]()
An application of Theorem 7.7.6 is illustrated in Section 7.7.6 (Figure 7.17).
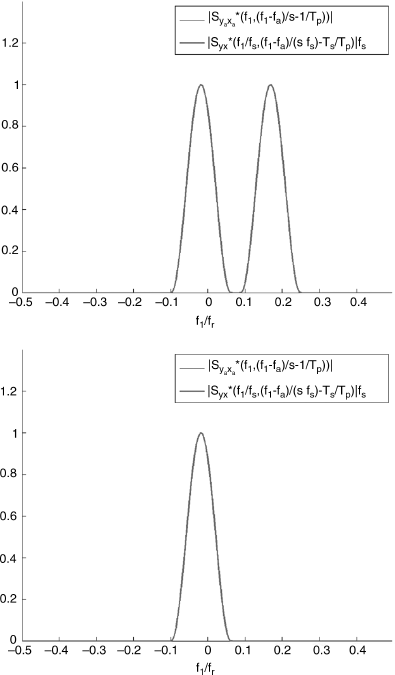
Figure 7.17 (Continuous-time) PAM signal xa(t) with raised cosine pulse and its Doppler-stretched version ![]() . Slice of the magnitude of the spectral cross-correlation density of the continuous-time signals ya(t) and xa(t) along the support line f2 = (f1 − fa)/s − 1/Tp (thin line) and of the rescaled (ν1 = f1/fs) spectral cross-correlation density of the discrete-time signals
. Slice of the magnitude of the spectral cross-correlation density of the continuous-time signals ya(t) and xa(t) along the support line f2 = (f1 − fa)/s − 1/Tp (thin line) and of the rescaled (ν1 = f1/fs) spectral cross-correlation density of the discrete-time signals ![]() and
and ![]() , along
, along ![]() (thick line) as a function of f1/fr. (top) fs = 2B′ [fs/2 = 0.25fr] and (bottom) fs = 4B′ [fs/2 = fr/2].
(thick line) as a function of f1/fr. (top) fs = 2B′ [fs/2 = 0.25fr] and (bottom) fs = 4B′ [fs/2 = fr/2].
Source: (Napolitano 2010b) Copyright of Elsevier
By inverse Fourier transforming both sides of (7.324) gives the following expression for the (conjugate) cyclic autocorrelation function of the Doppler-stretched signal ya(t) (see also (7.263) and (7.267))
Then, accounting for (1.174) the following aliasing formula for the (conjugate) cyclic autocorrelation function of y(n) is obtained
In (7.339), xas(t) ![]() xa(st) and, hence, according to (7.338) (with ya(t) = xa(st), A = 1, ϕ = 0, fa = 0, and da = 0) one has
xa(st) and, hence, according to (7.338) (with ya(t) = xa(st), A = 1, ϕ = 0, fa = 0, and da = 0) one has ![]() .
.
From (7.339), the following result can be derived.
Theorem 7.7.8 Sampling Theorem for the (Conjugate) Cyclic Autocorrelation Function (Napolitano 2010b, Theorem 7). Let xa(t) be ACS and band-limited with bandwidth B. For
one obtains
with ![]() . Equation (7.342) is the unaliased sampled version of (7.338).
. Equation (7.342) is the unaliased sampled version of (7.338).
Proof: See Section 7.10. ![]()
An expression for ![]() alternative to (7.341a) and (7.342b) can be obtained starting from (7.331). In fact, for fs ≥ 4(B|s| + |fa|) the (conjugate) cyclic autocorrelation function of y(n) can be expressed as
alternative to (7.341a) and (7.342b) can be obtained starting from (7.331). In fact, for fs ≥ 4(B|s| + |fa|) the (conjugate) cyclic autocorrelation function of y(n) can be expressed as
(7.342) 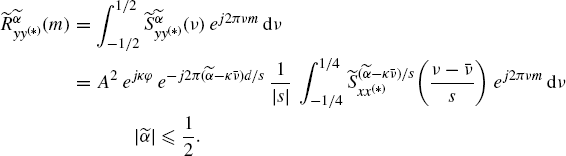
Finally, the cross-characterization of y(n) and x(n) is obtained by setting t = nTs and τ = mTs into (7.283)
(7.343) 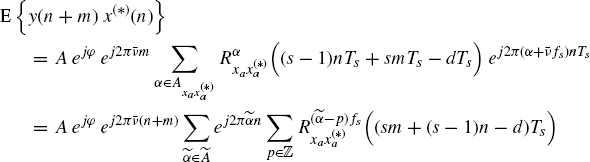
where ![]() is defined according to (1.171) and (1.172) and (sm + (s − 1)n − d) in general is non-integer.
is defined according to (1.171) and (1.172) and (sm + (s − 1)n − d) in general is non-integer.
Analogously to the continuous-time case, the cross-correlation ![]() does not contain any finite-strength additive sinewave component if s ≠ 1.
does not contain any finite-strength additive sinewave component if s ≠ 1.
7.7.6 Illustrative Examples
In this section, examples are presented aimed at illustrating the theoretical results of Section 7.7.5. These results, which are formulated in terms of Loève bifrequency spectra, can be equivalently expressed in terms of bifrequency spectral cross-correlation densities (4.19) by replacing Dirac with Kronecker deltas. For example, (7.276) becomes
where δγ denotes Kronecker delta, that is, δγ = 1 for γ = 0 and δγ = 0 for γ ≠ 0.
In the experiment, a PAM signal xa(t) is considered with stationary white modulating sequence, raised cosine pulse with excess bandwidth η, and symbol period Tp. It is second-order cyclostationary with period Tp and strictly bandlimited with bandwidth B = (1 + η)/(2Tp) which can be slightly overestimated by B′ = 1/Tp. Thus, it has three cycle frequencies αh = h/Tp, h ![]() {0, ± 1} (Gardner et al. 2006). Furthermore, η = 0.85 and Tp = 4/fr are assumed, where fr is a fixed reference frequency. The Doppler-stretched signal ya(t) in (7.261) has A = 1, ϕ = 0, da = 0, fa = 0.075fr, and s = 0.75.
{0, ± 1} (Gardner et al. 2006). Furthermore, η = 0.85 and Tp = 4/fr are assumed, where fr is a fixed reference frequency. The Doppler-stretched signal ya(t) in (7.261) has A = 1, ϕ = 0, da = 0, fa = 0.075fr, and s = 0.75.
In the figures, supports of impulsive functions are drawn as “checkerboard” plots with gray levels representing the magnitude of the density of the impulsive functions. In addition, for notation simplicity, the bifrequency SCD of signals a and b is denoted by ![]() . The bifrequency spectral correlation density
. The bifrequency spectral correlation density ![]() is the same as that in Figure 4.6. In Figure 7.10, (top) magnitude and (bottom) “checkerboard” plot of the bifrequency spectral correlation density
is the same as that in Figure 4.6. In Figure 7.10, (top) magnitude and (bottom) “checkerboard” plot of the bifrequency spectral correlation density ![]() are reported as functions of f1/fr and f2/fr. In Figures 7.11 and 7.12, the magnitude of the bifrequency spectral correlation density
are reported as functions of f1/fr and f2/fr. In Figures 7.11 and 7.12, the magnitude of the bifrequency spectral correlation density ![]() of the discrete-time signal
of the discrete-time signal ![]() , is represented as a function of ν1 and ν2 for two values of the sampling frequency. Specifically, in Figure 7.11 fs = 2|s|B′ and in Figure 7.12 fs = 4|s|B′ are considered. Since the support lines have unit slope, both continuous-and discrete-time signals are ACS. According to Theorem 7.7.3, fs = 2|s|B′ ≥ 2|s|B is a sufficient condition to assure non-overlapping replicas in the Loève bifrequency spectrum of ya(t). However, only the more stringent condition fs ≥ 2(B|s| + |fa|) can assure that (7.327) holds. For the considered numerical values, fs = 4|s|B′ is such that the sufficient conditions on fs of Theorems 7.7.5 and 7.7.6 are both satisfied.
, is represented as a function of ν1 and ν2 for two values of the sampling frequency. Specifically, in Figure 7.11 fs = 2|s|B′ and in Figure 7.12 fs = 4|s|B′ are considered. Since the support lines have unit slope, both continuous-and discrete-time signals are ACS. According to Theorem 7.7.3, fs = 2|s|B′ ≥ 2|s|B is a sufficient condition to assure non-overlapping replicas in the Loève bifrequency spectrum of ya(t). However, only the more stringent condition fs ≥ 2(B|s| + |fa|) can assure that (7.327) holds. For the considered numerical values, fs = 4|s|B′ is such that the sufficient conditions on fs of Theorems 7.7.5 and 7.7.6 are both satisfied.
In Figure 7.13, the slice of the magnitude of the spectral correlation density of the continuous-time signal ya(t) along the support line f2 = f1 − s/Tp (thin line) and of the rescaled (ν1 = f1/fs) spectral correlation density of the discrete-time signal ![]() along ν2 = ν1 − s(Ts/Tp) (thick line) as a function of f1/fr are reported (top) for fs = 2|s|B′ and (bottom) for fs = 4|s|B′. According with the results of Theorems 7.7.4 and 7.7.5, only in case fs = 4|s|B′ there are no aliasing replicas and the spectral correlation density of ya(t) (coincident with the cyclic spectrum) is equal to that rescaled of y(n) considered in the main frequency domain.
along ν2 = ν1 − s(Ts/Tp) (thick line) as a function of f1/fr are reported (top) for fs = 2|s|B′ and (bottom) for fs = 4|s|B′. According with the results of Theorems 7.7.4 and 7.7.5, only in case fs = 4|s|B′ there are no aliasing replicas and the spectral correlation density of ya(t) (coincident with the cyclic spectrum) is equal to that rescaled of y(n) considered in the main frequency domain.
Let us consider now the bifrequency spectral cross-correlation density ![]() between the jointly SC signals ya(t) and xa(t). Accounting for (7.344) we have
between the jointly SC signals ya(t) and xa(t). Accounting for (7.344) we have
where ![]() denote the cyclic spectra of the PAM signal xa(t).
denote the cyclic spectra of the PAM signal xa(t).
In Figure 7.14, (top) magnitude and (bottom) “checkerboard” plot of the spectral cross-correlation density (7.345) of the continuous-time signals ya(t) and xa(t) are reported as functions of f1/fr and f2/fr.
In Figures 7.15 and 7.16, the bifrequency spectral cross-correlation density ![]() of the discrete-time signals
of the discrete-time signals ![]() and
and ![]() is represented as a function of ν1 and ν2 for two values of the sampling frequency. Specifically, in Figure 7.15 fs = 2B′ and in Figure 7.16 fs = 4B′ are considered. Since B′ ≥ B ≥ B|s| + |fa|, due to Theorem 7.7.6, condition fs = 2B′ assures non-overlapping replicas in the Loève bifrequency cross-spectrum, and, hence, in its bifrequency density
is represented as a function of ν1 and ν2 for two values of the sampling frequency. Specifically, in Figure 7.15 fs = 2B′ and in Figure 7.16 fs = 4B′ are considered. Since B′ ≥ B ≥ B|s| + |fa|, due to Theorem 7.7.6, condition fs = 2B′ assures non-overlapping replicas in the Loève bifrequency cross-spectrum, and, hence, in its bifrequency density ![]() . However, such a condition does not assure, for each support line, the mapping in the whole principal frequency domain between spectral densities of continuous-and discrete-time signals. In fact, in Figure 7.17, the slice of the magnitude of the spectral cross-correlation density of the continuous-time signals ya(t) and xa(t) along the support line f2 = (f1 − fa)/s − 1/Tp (thin line) and of the rescaled (ν1 = f1/fs) spectral cross-correlation density of the discrete-time signals
. However, such a condition does not assure, for each support line, the mapping in the whole principal frequency domain between spectral densities of continuous-and discrete-time signals. In fact, in Figure 7.17, the slice of the magnitude of the spectral cross-correlation density of the continuous-time signals ya(t) and xa(t) along the support line f2 = (f1 − fa)/s − 1/Tp (thin line) and of the rescaled (ν1 = f1/fs) spectral cross-correlation density of the discrete-time signals ![]() and
and ![]() along
along ![]() (thick line) as a function of f1/fr is reported (top) for fs = 2B′ and (bottom) for fs = 4B′. According to Theorem 7.7.7 and due to the numerical values of s and fa, only condition fs = 4B′ assures the lack of aliasing replicas in the considered cross-spectral density function. In such a case, the spectral cross-correlation density of the continuous-time signals and that rescaled of the discrete-time signals are coincident in the principal frequency domain.
(thick line) as a function of f1/fr is reported (top) for fs = 2B′ and (bottom) for fs = 4B′. According to Theorem 7.7.7 and due to the numerical values of s and fa, only condition fs = 4B′ assures the lack of aliasing replicas in the considered cross-spectral density function. In such a case, the spectral cross-correlation density of the continuous-time signals and that rescaled of the discrete-time signals are coincident in the principal frequency domain.
7.7.7 Concluding Remarks
The Loève bifrequency spectrum is used as framework to describe in the spectral domain the nonstationarity of a Doppler-stretched signal when the transmitted signal is ACS. Even if the Doppler channel is linear not almost-periodically time-variant, the received signal is still ACS. The transmitted and received signals are jointly SC with spectral masses in the bifrequency plane concentrated on lines with slope equal to the reciprocal of the time-scale factor introduced by the Doppler channel. Sampling theorems are proved for spectral statistical functions characterizing the Doppler-stretched received signal and jointly characterizing the transmitted and received signals. Sufficient conditions are found in terms of sampling frequency fs, transmitted signal bandwidth B, frequency-shift fa, and time-scale factor s. For the ACS Doppler-stretched signal, fs ≥ 2B|s| and fs ≥ 2(B|s| + |fa|) assure, in the Loève bifrequency spectrum of the sampled signal, no overlap of replicas and main replica in the principal frequency domain, respectively (Theorem 7.7.3); fs ≥ 2(2B|s| + |fa|) guarantees the mapping between spectral densities of the continuous-and discrete-time signals in the whole principal frequency domain (Theorem 7.7.4); fs ≥ 4(B|s| + |fa|) assures that the main replica of the (conjugate) cyclic spectrum is in the principal spectral and cycle frequency domain (Theorem 7.7.5). For the jointly SC transmitted and received Doppler-stretched signals, fs ≥ max {2B|s|, 2B} and fs ≥ max {2(B|s| + |fa|), 2B} assure, in the Loève bifrequency cross-spectrum, no overlap of replicas and main replica in the principal frequency domain, respectively (Theorem 7.7.6); fs ≥ max {2(B|s| + |fa|), 4B} provides the mapping between cross-spectral densities of the continuous-and discrete-time signals in the whole principal frequency domain (Theorem 7.7.7). Condition fs ≥ 4B|s| is sufficient to avoid aliasing in the cycle-frequency domain for the (conjugate) cyclic autocorrelation function (Theorem 7.7.8).
It is worth observing that in communications and radar applications the several obtained bounds on fs can be reduced to the two bounds fs ≥ 2B and fs ≥ 4B since |s| ![]() 1 and |fa| < B can be generally assumed. Such conditions, however, do not hold in sonar and acoustic aircraft applications (Ferguson 1999; Weiss 1994). The derived lower bounds for the sampling frequency are such that relationships in continuous-time linking spectral statistical functions of transmitted ACS and received Doppler-stretched signals are formally analogous to their discrete-time counterparts. Thus, signal-parameter estimation procedures described in continuous-time in (De Angelis et al. 2005) and (Napolitano and Do
1 and |fa| < B can be generally assumed. Such conditions, however, do not hold in sonar and acoustic aircraft applications (Ferguson 1999; Weiss 1994). The derived lower bounds for the sampling frequency are such that relationships in continuous-time linking spectral statistical functions of transmitted ACS and received Doppler-stretched signals are formally analogous to their discrete-time counterparts. Thus, signal-parameter estimation procedures described in continuous-time in (De Angelis et al. 2005) and (Napolitano and Do![]() ançay 2011) can be straightforwardly implemented in discrete-time by substituting cyclic spectra of continuous-time signals with cyclic spectra of their sampled versions and integrals with sums.
ançay 2011) can be straightforwardly implemented in discrete-time by substituting cyclic spectra of continuous-time signals with cyclic spectra of their sampled versions and integrals with sums.