Problem 3.5
Optimal transaction costs from a
Stackelberg perspective
Geert Jan Olsder
Faculty of Information Technology and Systems
Delft University of Technology
P.O. Box 5031, 2600 GA Delft
The Netherlands
1 DESCRIPTION OF THE PROBLEM
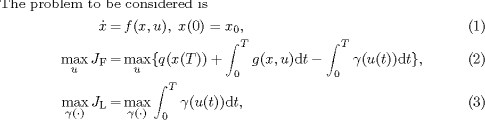
2 MOTIVATION AND HISTORY OF THE PROBLEM
3 AVAILABLE RESULTS AND BACKGROUND
Problems with transaction costs have been studied before, see e.g., [1, 3, 4], but never from the point of view of the bank to maximize these costs. The problem as stated is a difficult one, see [7] for some first solution attempts. The principal difficulty is that composed functions are involved, i.e., one function is the argument of another [6]. Hence, we will also consider the following static problem, which is simpler than the time-dependent one:
To start with, in a conventional Stackelberg game, there are two players, called Leader and Follower respectively, each having their own cost function
where 
. Each player wants to choose his own decision variable in such a way as to maximize his own criterion. Without giving an
equilibrium concept, the problem as stated so far is not well defined. Such an equilibrium concept could, for instance, be
one named after Nash or Pareto. In the Stackelberg equilibrium concept, one player, the Leader, announces his decision uL,
which is subsequently known to the other player, the Follower.
With this knowledge, the Follower chooses his 
. Hence, becomes a function of 
, written as
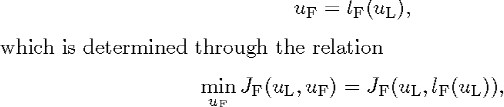
provided that this minimum exists and is a singleton for each possible choice of the Leader. The function 
is sometimes called a reaction function.
Before the Leader announces his decision , he will realize how the Follower will react and hence the Leader chooses uL such as to minimize
BIBLIOGRAPHY
[1] M. Akian, J. L. Menaldi, and A. Sulem, “On an investment-consumption model with transaction costs, ” SIAM J. Control and Optim., vol. 34 pp.
329-364, 1996.
[2] T. 
and G. J. Olsder, Dynamic Noncooperative Game Theory, SIAM, Philadelphia, 1999.
[3] P. Bernhard, “A robust control approach to option pricing including transaction costs, ” In: Annals of the ISDG 7, A.Nowak, ed., Birkhäuser, 2002.
[4] E. R. Grannan and G. H. Swindle, “Minimizing transaction costs of option hedging strategies, ” Mathematical finance, vol. 6, no. 4, 341–364, 1996.
[5] Y.-C. Ho, P. B. Luh and G. J. Olsder, “A control-theoretic view on incentives, ” Automatica, vol. 18, pp. 167-179, 1982.
[6] M. Kuczma, Functional Equations in a Single Variable, Polish Scientific Publishers, 1968.
[7] G. J. Olsder, “Differential game-theoretic thoughts on option pricing and transaction costs, ” International Game Theory Review, vol. 2, pp. 209 228, 2000.