Problem 6.1
Copositive Lyapunov functions
M. K. 
amlibel
Department of Mathematics
University of Groningen
P.O. Box 800, 9700 AV Groningen
The Netherlands
J. M. Schumacher
Department of Econometrics and Operations Research
Tilburg University
P.O. Box 90153, 5000 LE Tilburg
The Netherlands
1 PRELIMINARIES
2 MOTIVATION
Lyapunov stability theory is one of the ever green topics in systems and control. For (finite dimensional) linear systems, the following theorem is very well-known.
Theorem 1:[3, Theorem 1.2]: The following conditions are equivalent.
1. The system 
= Ax is asymptotically stable.
2. The Lyapunov equation 
has a positive definite symmetric solution P for any negative definite symmetric matrix Q.
As a refinement, we can replace the last statement by
2. The Lyapunov equation has a positive definite symmetric solution P for any nonpositive definite symmetric matrix Q such that the pair (A, Q) is observable.
An interesting application is to the stability of the so-called switched systems. Consider the system
where the switching signal 
is a piecewise constant function. We assume that it has a finite number of discontinuities over finite time intervals in
order to rule out infinitely fast switching. A strong notion of stability for the system (1) is the requirement of stability
for arbitrary switching signals.
The dynamics of (1) coincides with one of the linear subsystems if the switching signal is constant, i.e., there are no switchings at all. This leads us to an obvious necessary condition: stability of each subsystem. Another extreme case would emerge if there exists a common Lyapunov function for the subsystems. Indeed, such a Lyapunov function would immediately prove the stability of (1). An earlier paper [8] pointed out the importance of commutation relations between A1 and A2 in finding a common Lyapunov function. More precisely, it has been shown that if A1 and A2 are Hur-witz and commutative then they admit a common Lyapunov function. In [1, 6], the commutation relations of subsystems are studied further in a Lie algebraic framework and sufficient conditions for the existence of a common Lyapunov function are presented. Notice that the results of [1] are stronger than those in [6]. However, we prefer to restate [6, Theorem 2] for simplicity.
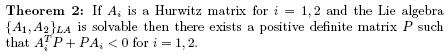
So far, we quoted some known results. Our main goal is to pose two open problems that can be viewed as extensions of Theorems 2 and 2 for a class of piecewise linear systems. More precisely, we will consider systems of the form
One way of studying the stability of the system (2) is simply to utilize Theorem 2. However, there are some obvious drawbacks:
i. It requires positive definiteness of the common Lyapunov function whereas the positivity on a cone is enough for the system (2).
ii. It considers any switching signal whereas the initial state determines the switching signal in (2).
In the next section, we focus on ways of eliminating the conservatism mentioned in 2.
3 DESCRIPTION OF THE PROBLEMS
4 ON COPOSITIVE MATRICES
This last section discusses copositive matrices in order to provide a starting point for further investigation of the proposed problems.
The class of copositive matrices occurs in optimization theory and particularly in the study of the linear complementarity problem [2]. We quote from [4] the following theorem which provides a characterization of copositive matrices.
Theorem 2. A symmetric matrix M is (strictly) copositive with respect to the cone 
if and only if every principal submatrix of M has no eigenvector 
with associated eigenvalue 
Since the number of principal submatrices of a matrix of order n is roughly 2n, this result has a practical disadvantage. In fact, Murty and Kabadi [7] showed that testing for copositivity is NP-complete. An interesting subclass of copositive matrices are the ones that are equal to the sum of a nonnegative definite matrix and a non-negative matrix. This class of matrices is studied in [5] where a relatively more tractable algorithm has been presented for checking if a given matrix belongs to the class or not.