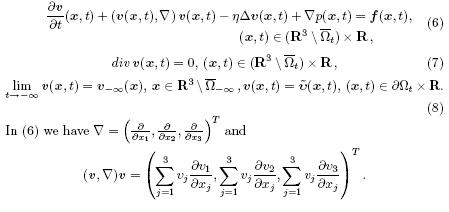Problem 5.6

In recent years, as a consequence of the dramatic increases in computing power and of the continuing refinement of the numerical algorithms available, the numerical treatment of control problems for systems governed by partial differential equation; see, for example, [1], [3], [4], [5], [8]. The importance of these mathematical problems in many applications in science and technology cannot be overemphasized.

The most common approach to a control problem for a system governed by partial differential equations is to see the problem as a constrained nonlinear optimization problem in infinite dimension. After discretization the problem becomes a finite dimensional constrained nonlinear optimization problem that can be attacked with the usual iterative methods of nonlinear optimization, such as Newton or quasi-Newton methods. Note that the problem of the convergence, when the “discretization step goes to zero, ” of the solutions computed in finite dimension to the solution of the infinite dimensional problem is a separate question and must be solved separately. When this approach is used an objective function evaluation in the nonlinear optimization procedure involves the solution of the partial differential equations that govern the system. Moreover, the evaluation of the gradient or Hessian of the objective function involves the solution of some kind of sensitivity equations for the partial differential equations considered. The nonlinear optimization procedure that usually involves function, gradient and Hessian evaluation is computationally very expensive.

This fact is a serious limitation to the use of control problems for systems governed by partial differential equations in real situations. However the approach previously described is very straightforward and does not use any of the special features present in every system governed by partial differential equations. So that, at least in some special cases, it should be possible to improve on this straightforward approach.

The purpose of this paper is to point out a problem, see [6], [2], where a new approach, that greatly improves on the previously described one, has been introduced and to suggest some other problems where, hopefully, similar improvements can be obtained. In particular, we propose two control problems of great relevance in several applications in science and technology and we suggest the (open) question of characterizing the optimal solution of these control problems as the solution of suitable systems of partial differential equations. If this question has an affirmative answer, high performance algorithms can be developed to solve the control problems proposed. Note that in [6], [2] this characterization has been made for some control problems in acoustics, thanks to the use of the Pontryagin maximum principle, and has permitted to develop high performance algorithms to solve these control problems. Moreover, we suggest the (open) question of using effectively the dynamic programming method to derive closed loop control laws for the control problems considered. For effective use of the dynamic programming method, we mean the possibility of computing a closed loop control law at approximately the same computational cost of solving the original problem when no control strategy is involved.

In section 2 we summarize the results obtained in [6], [2], and in section 3 we present two problems that we believe can be approached in a way similar to the one described in [6], [2].

2 PREVIOUS RESULTS

In [6], [2] a furtivity problem in time dependent acoustic obstacle scattering is considered. An obstacle of known acoustic impedance is hit by a known incident acoustic field. When hit by the incident acoustic field, the obstacle generates a scattered acoustic field. To make the obstacle furtive means to “minimize” the scattered field. The furtivity effect is obtained circulating on the boundary of the obstacle a “pressure current” that is a quantity whose physical dimension is: pressure divided by time. The problem consists in finding the optimal “pressure current” that “minimizes” the scattered field and the “size” of the pressure current employed. The mathematical model used to study this problem is a control problem for the wave equation, where the control function (i.e., the pressure current) influences the state variable (i.e., the scattered field) through a boundary condition imposed on the boundary of the obstacle, and the cost functional depends explicitly from both the state variable and the control function. Introducing an auxiliary variable and using the Pontryagin maximum principle (see [7]) in [6], [2] it is shown that the optimal control of this problem can be obtained from the solution of a system of two coupled wave equations. This system of wave equations is equipped with suitable initial, final, and boundary conditions. Thanks to this ingenious construction the solution of the optimal control problem can be obtained solving the system of wave equations without the necessity of going through the iterations implied in general by the nonlinear optimization procedure. This fact avoids many of the difficulties, that have been mentioned above, present in the general case. Finally, the system of wave equations is solved numerically using a highly parallelizable algorithm based on the operator expansion method (for more details, see [6], [2] and the references therein). Some numerical results obtained with this algorithm on simple test problems can be seen in the form of computer animations in the websites: http://www.econ.unian.it/recchioni/w6, http://www.econ.unian.it/recchioni/w8. In the following section, we suggest two problems where will be interesting to carry out a similar analysis.

3 TWO CONTROL PROBLEMS

17269