Problem 9.1

A conjecture on Lyapunov equations and

principal angles in subspace identification

Katrien De Cock and Bart De Moor¹

Dept. of Electrical Engineering (ESAT–SCD)

K.U.Leuven

Kasteelpark Arenberg 10

B-3001 Leuven

Belgium

http://www.esat.kuleuven.ac.be/sista-cosic-docarch

[email protected],[email protected]

1 DESCRIPTION OF THE PROBLEM

The following conjecture relates the eigenvalues of certain matrices that are derived from the solution of a Lyapunov equation that occurred in the analysis of stochastic subspace identification algorithms [3]. First, we formulate the conjecture as a pure matrix algebraic problem. In Section 2, we will describe its system theoretic consequences and interpretation.

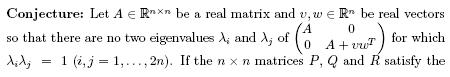
Lyapunov equation

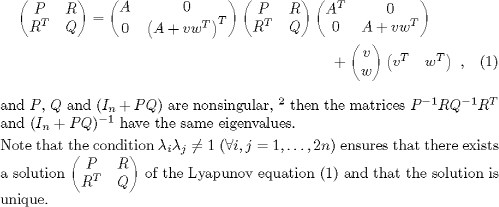
We have checked the similarity of for numerous examples (“proof by Matlab”) and it is simple to prove the conjecture for n = 1. Furthermore, via a large detour (see [3]) we can also prove it from the system theoretic interpretation, which is given in section 5. However, we have not been able to find a general and elegant proof.

We also remark that the requirement that v and w are vectors is necessary for the conjecture to hold. One can easily find counterexamples for the case It is consequently clear that this condition on v and w should be used in the proof.

2 BACKGROUND AND MOTIVATION

Although the conjecture is formulated as a pure matrix algebraic problem, its system theoretic interpretation is particularly interesting. In order to explain the consequences, we first have to introduce some concepts: the principal angles between subspaces (section 3) and their statistical counterparts, the canonical correlations of random variables (section 4). Next, in section 5 we will show how the conjecture, when proved correct, would enable us to prove in an elegant way that the nonzero canonical correlations of the past and the future of the output process of a linear stochastic model are equal to the sines of the principal angles between two specific subspaces that are derived from the model. This result, in its turn, is instrumental for further derivations in [3], where a cepstral distance measure is related to canonical correlations and to the mutual information of two processes (see also section 5). Moreover, by this new characterization of the canonical correlations, we gain insight in the geometric properties of subspace based techniques.

3 THE PRINCIPAL ANGLES BETWEEN TWO SUBSPACES

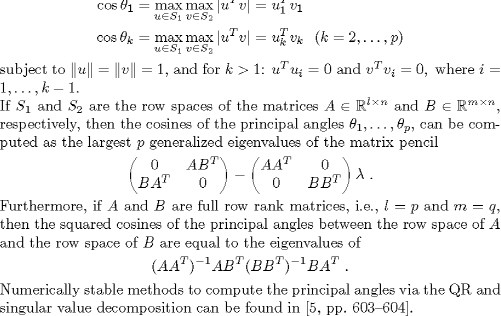
4 THE CANONICAL CORRELATIONS OF TWO RANDOM VARIABLES

Canonical correlation analysis, due to Hotelling [6], is the statistical version of the notion of principal angles.

Let X 2 Rp and Y 2 Rq, where p q, be zero-mean random variables with full rank joint covariance matrix³

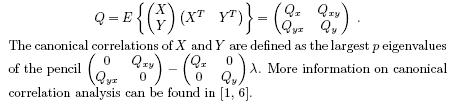
5 SYSTEM THEORETIC

INTERPRETATION OF CONJECTURE

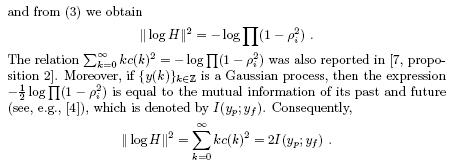
6 CONCLUSIONS

We presented a matrix algebraic conjecture on the eigenvalues of matrices that are derived from the solution of a Lyapunov equation. We showed that a proof of conjecture 1 would provide yet another elegant geometric result in the subspace based study of linear stochastic systems. Moreover, it can be used to express a cepstral distance measure that was defined in [9] in terms of canonical correlations and also as the mutual information of two processes.

BIBLIOGRAPHY

[1] T. W. Anderson, An Introduction to Multivariate Statistical Analysis, John Wiley & Sons, New York, 1984.

[2] K. De Cock and B. De Moor, “Subspace angles between ARMA models, ” Technical Report⁴ 00-44a, ESAT-SCD, K.U.Leuven, Leuven, Belgium, accepted for publication in Systems Control Letters, 2002.

[3] K. De Cock, Principal Angles in System Theory, Information Theory and Signal Processing, Ph.D. thesis, ⁵ Faculty of Applied Sciences, K.U.Leuven, Leuven, Belgium, 2002.

[4] I. M. Gel’fand and A. M. Yaglom, “Calculation of the amount of information about a random function contained in another such function, ”American Mathematical Society Translations, Series (2), 12, pp. 199– 236, 1959.

[5] G. H. Golub and C. F. Van Loan, Matrix Computations, The Johns Hopkins University Press, Baltimore, 1996.

[6] H. Hotelling, “Relations between two sets of variates, ” Biometrika, 28, pp. 321–372, 1936.

[7] N. P. Jewell, P. Bloomfield, and F. C. Bartmann, “Canonical correlations of past and future for time series: Bounds and computation, ” The Annals of Statistics, 11, pp. 848–855, 1983.

[8] C. Jordan, “Essai sur la géométrie à n dimensions, ” Bulletin de la Société Mathematique, 3, pp. 103–174, 1875.

[9] R. J. Martin, “A metric for ARMA processes, ”, IEEE Transactions on Signal Processing, 48, pp. 1164–1170, 2000.

[10] A. V. Oppenheim and R. W. Schafer, Digital Signal Processing, Pren-tice/ Hall International, 1975.

1Katrien De Cock is a research assistant at the K.U.Leuven. Dr. Bart De Moor is a full professor at the K.U.Leuven. Our research is supported by grants from several funding agencies and sources: Research Council KUL: Concerted Research Action GOA-Mefisto 666, IDO, several Ph.D., postdoctoral & fellow grants; Flemish Government: Fund for Scientific Research Flanders (several Ph.D. and postdoctoral grants, projects G.0256.97,

G.0115.01, G.0240.99, G.0197.02, G.0407.02, research communities ICCoS, ANMMM), AWI (Bil. Int. Collaboration Hungary/ Poland), IWT (Soft4s, STWW-Genprom, GBOU-McKnow, Eureka-Impact, Eureka-FLiTE, several PhD grants); Belgian Federal Govern-ment: DWTC (IUAP IV-02 (1996-2001) and IUAP V-22 (2002-2006)), Program Sustainable Development PODO-II (CP/40); Direct contract research: Verhaert, Electrabel, Elia, Data4s, IPCOS.

2The matrix In is the n × n identity matrix.

3E {.} is the expected value operator.

4This report is available by anonymous ftp from ftp.esat.kuleuven.ac.be in the directory pub/sista/reports as file 00-44a.ps.gz.

5This thesis will also be made available by anonymous ftp from ftp.esat.kuleuven.ac.be as file pub/sista/decock/reports/phd.ps.gz