Problem 5.3
Null-controllability of the heat equation
in unbounded domains
Sorin Micu
Facultatea de Matematic
-Informatica
Universitatea din Craiova
Al. I. Cuza 13, Craiova, 1100
Romania
Enrique Zuazua
Departamento de Matemáticas, Facultad de Ciencias
Universidad Autónoma
Cantoblanco, 28049, Madrid
Spain
1 DESCRIPTION OF THE PROBLEM
2 MOTIVATION AND HISTORY OF THE PROBLEM
We begin with the following well-known result
Theorem 1. When 
is a bounded domain of class C2 system (1) is null-controllable for any T > 0.
We refer to D. L. Russell [12] for some particular examples treated by means of moment problems and Fourier series and to
A. Fursikov and O. Yu. Imanuvilov [3] and G. Lebeau and L. Robbiano [7] for the general result covering any bounded smooth
domain and open, nonempty subset 
of 
. Both the approaches of [3] and [7] are based on the use of Carleman inequalities.
However, in many relevant problems the domain is unbounded. We address the following question: if is an unbounded domain, is system (1) null-controllable for some T > 0?.
None of the approaches mentioned above apply in this situation. In fact, very particular cases being excepted (see the following
section), there exist no results on the null-controllability of the heat equation (1) when is unbounded.
The approach described in [6] and [9] is also worth mentioning. In this article it is proved that, for any T > 0, the heat
equation has a fundamental solution that is 
Caway from the origin and with support in the strip 
. This fundamental solution, of course, grows very fast as |x|goes to infinity. As a consequence of this, a boundary controllability
result may be immediately obtained in any domain with controls distributed all along its boundary. Note, however, that when the domain is unbounded the solutions and controls
obtained in this way grow too fast as 
and, therefore, these are not solutions in the classical sense. In fact, in the frame of unbounded domains, one has to be
very careful in defining the class of admissible controlled solutions. When imposing, for instance, the classical integrability
conditions at infinity, one is imposing additional restrictions that may determine the answer to the controllability problem.
This is indeed the case, as we shall explain.
control on the approximating bounded domain 
. But this approach does not apply in the context of the null-control problem.
However, taking into account that approximate controllability holds, it is natural to analyze whether null-controllability holds as well.
In [1] it was proved that the null-controllability property holds even in unbounded domains if the control is supported in
a subdomain that only leaves a bounded set uncontrolled. Obviously, this result is very close to the case in which the domain
is bounded and does not answer to the main issue under consideration of whether heat processes are null-controllable in unbounded
domains.
3 AVAILABLE RESULTS
To our knowledge, in the context of unbounded domains and the boundary control problem, only the particular case of the half-space has been consid-ered:
When is bounded, Carleman inequalities provide the estimate (5) and, consequently, null-controllability holds (see, for instance, [3]). In the case of a half-space, by using a translation argument, it is easy to see that (5) does not hold (see [11]).
In the case of bounded domains, by using Fourier series expansion, the control problem may be reduced to a moment problem. However, Fourier series cannot be used directly in 
. Nevertheless, it was observed by M. Es-cobedo and O. Kavian in [2] that, on suitable similarity variables and at the appropriate
scale, solutions of the heat equation on conical domains may be indeed developed in Fourier series on a weighted 
-space. This idea was used in [10] and [11] to study the null-controllability property when is given by (3).
Firstly, we use similarity variables and weighted Sobolev spaces to develop the solutions in Fourier series. A sequence of
one-dimensional controlled systems like those studied in [10] is obtained. Each of these systems is equivalent to a moment
problem of the following type: given S > 0 and 
(depending on the Fourier coefficients of the initial data 
) find 
such that
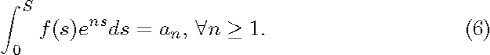
Theorem 2. When is the half line, there is no nontrivial initial datum u0 belonging to a negative Sobolev space that is null-controllable
in finite time with boundary controls.
This negative result was complemented by showing that there exist initial data with exponentially growing Fourier coefficients
for which null-controllability holds in finite time with -controls.
We mention that in [10] and [11] we are dealing with solutions defined in the sense of transposition, and therefore the solutions in [6] and [9] that grow and oscillate very fast at infinity are excluded.
4 OPEN PROBLEMS
As we have already mentioned, the null-controllability property of (1) when is unbounded and different from a half-line or half-space is still open.
The approach based on the use of the similarity variables may still be used in general conical domains. But, due to the lack of orthogonality of the traces of the normal derivatives of the eigenfunctions, the corresponding moment problem is more complex and remains to be solved.
When is a general unbounded domain, the similarity transformation does not seem to be of any help since the domain one gets after
transformation depends on time. Therefore, a completely different approach seems to be needed when is not conical. However, one may still expect a bad behavior of the null-control problem. Indeed, assume for instance that
contains . If one is able to control to zero in an initial data u0 by means of a boundary control acting on × (0, T), then, by restriction, one is able to control the initial
data | with the control being the restriction of the solution in the larger domain 
A careful development of this argument and of the result it may lead to remains to be done.
ACKNOWLEDGEMENTS
The first author was partially supported by Grant PB96-0663 of DGES (Spain) and Grant A3/2002 of CNCSIS (Romania). The second author was partially supported by Grant PB96-0663 of DGES (Spain) and the TMR network of the EU “Homogenization and Multiple Scales (HMS2000).”
BIBLIOGRAPHY
[1] V. Cabanillas, S. de Menezes and E. Zuazua, “Null controllability in unbounded domains for the semilinear heat equation with nonlinearities involving gradient terms, ” J. Optim. Theory Applications, 110 (2) (2001), 245-264.
[2] M. Escobedo and O. Kavian, “Variational problems related to self-similar solutions of the heat equation, ” Nonlinear Anal. TMA, 11 (1987), 1103-1133.
[3] A. Fursikov and O. Yu. Imanuvilov, “Controllability of evolution equations, ” Lecture Notes Series #34, Research Institute of Mathematics, Global Analysis Research Center, Seoul National University, 1996.
[4] J. M. Ghidaglia, “Some backward uniqueness results, ” Nonlinear Anal. TMA, 10 (1986), 777-790.
[5] O. Yu. Imanuvilov and M. Yamamoto, “Carleman estimate for a parabolic equation in Sobolev spaces of negative order and its applications, ” In: Control of Nonlinear Distributed Parameter Systems, G. Chen et al. eds., MarcelDekker, 2000, pp. 113-137.
[6] B. F. Jones, Jr., “A fundamental solution of the heat equation which is supported in a strip, ” J. Math. Anal. Appl., 60 (1977), 314-324.
[7] G. Lebeau and L. Robbiano, “Control
e exact de l’equation de la chaleur, ” Comm. P.D.E., 20 (1995), 335-356.
[8] J. L. Lions and E. Malgrange, “Sur l’unicit
e retrograde dans les problèmes mixtes paraboliques, ” Math. Scan., 8 (1960), 277-286.
[9] W. Littman, “Boundary control theory for hyperbolic and parabolic partial differential equations with constant coefficients, ”Annali Scuola Norm. Sup. Pisa, Serie IV, 3 (1978), 567-580.
[10] S. Micu and E. Zuazua, “On the lack of null-controllability of the heat equation on the half-line, ” Trans. AMS, 353 (2001), 1635-1659.
[11] S. Micu and E. Zuazua, “On the lack of null-controllability of the heat equation on the half-space, ” Portugalia Matematica, 58 (2001), 1-24.
[12] D. L. Russell, “Controllability and stabilizability theory for linear partial differential equations. Recent progress and open questions, ” em SIAM Rev., 20 (1978), 639-739.
[13] L. de Teresa and E. Zuazua, “Approximate controllability of the heat equation in unbounded domains, ” Nonlinear Anal. TMA, 37 (1999), 1059-1090.