Problem 2.2

On the stability of random matrices

Giuseppe Calafiore*, Fabrizio Dabbene**

*Dip. di Automatica e Informatica

**IEIIT-CNR Politecnico di Torino

C.so Duca degli Abruzzi, 24 Torino,

Italy

{giuseppe.calafiore, fabrizio.dabbene}@polito.it

1 INTRODUCTION AND MOTIVATION

The objective of this note is to encourage research on random matrices in the control community. The one who adventures in this field will encounter unexpected and exciting connections among different fields of science and beautiful branches of mathematics.

In the next section, we resume some of the known results on random matrices, and state a simple new (to the best of our knowledge) closed form result on the probability of stability of a certain class of random matrices. Then, in section 3 we propose three open problems related to the analytical assessment of the probability of stability of random matrices. The problems are presented in what we believe is their order of difficulty.

2 AVAILABLE RESULTS

2.1 Probability of stability for the ensemble

3 OPEN PROBLEMS

The probability of stability can be computed also for the GOEn ensemble and the ensemble, using a technique of integration over alternate variables. We pose this as the first open problem (of medium difficulty):

Problem 1: Determine the probability of stability for the GOEn and the ensembles.

A much harder problem would be to determine an analytic expression for the density of the eigenvalues (which are now both real and complex) of Gaussian matrices Gn, and then integrate it to obtain the probability of stability for the Gn ensemble:

Problem 2: Determine the probability of stability for the Gn ensemble.

A numerical estimate of the probability of (Hurwitz) stability for Gn matrices is reported in table 2.2.1, as a function of dimension n.

As the reader may have noticed, all the problems treated so far relate to random matrices with zero mean. From the point of view of robustness analysis it would be much more interesting to consider the case of biased random matrices. This motivates our last (and most difficult) open problem:

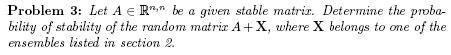
ACKNOWLEDGEMENTS

The authors wish to thank Professor Madan Lal Mehta for reading and giving his precious advice on this manuscript.

BIBLIOGRAPHY

[1] T. W. Anderson, An Introduction to Multivariate Statistical Analysis, John Wiley & Sons, New York, 1958.

[2] V. D. Blondel and J. N. Tsitsiklis, “A survey of computational complexity results in systems and control, ” Automatica, 36:1249–1274, 2000.

[3] G. Calafiore, F. Dabbene, and R. Tempo, “Randomized algorithms for probabilistic robustness with real and complex structured uncertainty, ” IEEE Trans. Aut. Control, 45(12):2218–2235, December 2000.

[4] A. Edelman, Eigenvalues and Condition Numbers of Random Matrices, Ph.D. thesis, Massachusetts Institute of Technology, Boston, 1989.

[5] A. Edelman, “How many eigenvalues of a random matrix are real?”, J.

Amer. Math. Soc., 7:247–267, 1994.

[6] V. L. Girko, Theory of Random Determinants, Kluwer, Boston, 1990.

[7] M. L. Mehta, Random Matrices, Academic Press, Boston, 1991.

[8] E. P. Wigner, “Distribution laws for the roots of a random Hermitian matrix, ” In C. E. Porter, ed., Statistical Theories of Spectra: Fluctuations. Academic, New York, 1965.

[9] E. P. Wigner, “Statistical properties of real symmetric matrices with many dimensions, ” In C. E. Porter, ed., Statistical Theories of Spectra:

Fluctuations. Academic, New York, 1965.