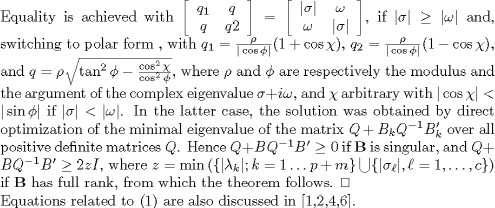Problem 1.11

Riccati stability

Erik I. Verriest¹

School of Electrical and Computer Engineering

Georgia Institute of Technology

Atlanta, GA, 30332-0250

USA

[email protected]

1 DESCRIPTION OF THE PROBLEM

Given two n×n real matrices, A and B, consider the matrix Riccati equation

Can one characterize the pairs (A, B) for which the above equation has a solution for positive definite symmetric matrices P, Q, and R?

In [8] a pair (A, B) was defined to be Riccati stable if a triple of positive definite matrices P, Q, R exists such that (1) holds.

The problem may be stated equivalently as an LMI:

Can one characterize all pairs (A, B) without invoking additional matrices, for which there exist positive definite matrices P and Q such that

2 MOTIVATION AND HISTORY OF THE PROBLEM

Equation (1) plays an important role in the stability analysis of linear time-invariant delay-differential systems. It is known [9] that the autonomous system

is asymptotically stable, for all values if the pair (A, B) is Riccati stable. Note that since (3) has to be stable for r= 0 and , the matrices A + B and A have to be Hurwitz stable, i.e., has its spectrum in the open left half plane. Recall also that a matrix C is Schur-Cohn stable, if its spectrum lies in the open unit disk.

If B = 0, thus reducing the problem to a finite dimensional time-invariant system, the Riccati equation reduces to the ubiquitous Lyapunov equation,

where we have set Q + R = S. It is well known that a positive definite pair (P, S) exists if and only if A is Hurwitz. This condition is necessary and sufficient.

The above result and its equivalent LMI formulation, initiated a whole set of extensions: for multiple delays, distributed delays, time-variant systems (with time-variant delays) [3, 5]. In addition all the above variants can further be extended to include parameter variations (robust stability) and noise (stochastic stability). Also other types of functional differential equations (scale delay) lead to such conditions [7]. The main idea in deriving these results is the use of the Lyapunov-Krasovskii theory with appropriate Lya-punov functionals. The equation (1) appears also in control theory and in game theory.

3 AVAILABLE RESULTS

Riccati-stable.

The full rank condition on B can be relaxed. Lemma 3 is a duality result.

In [8] a detailed construction was given for a subset of Riccati-stable pairs for the case n = 2. It leads to an (over-)parameterization, but the construction readily extends to arbitrary dimensions, by using

Theorem 4: Assume that the pairs {(Ai, Bi) | i = 1 . . .N} are Riccati-stable for the same P-matrix. i.e., there exist Qi, Ri > 0, i = 1 . . .N such that

The invariance of Riccati-stability under similarity (lemma 2) ensures that if (A, B) is Riccati-stable, one can transform the system to one for which the new P matrix, i.e., is the identity. Thus motivated, we provide a simplified form:

Given B, denote by AB the set of matrices A for which (A, B) is Riccati stable, with P = I, i.e.,

Hence, a necessary condition for A AB is that its symmetric part As satisfies