Problem 1.13

Projection of state space realizations

Antoine Vandendorpe and Paul Van Dooren

Department of Mathematical Engineering

Université catholique de Louvain

B-1348 Louvain-la-Neuve

Belgium

1 DESCRIPTION OF THE PROBLEM

We consider two m × p strictly proper transfer functions

2 MOTIVATION AND HISTORY OF THE PROBLEM

Equation (2) arises naturally in the general framework of model reduction of large scale linear systems [1]. In this context we are given a transfer function T(s) of McMillan degree n, which we want to approximate by a transfer function of smaller McMillan degree k, in order to solve a simpler analysis or design problem.

Classical model reduction techniques include modal approximation (where the dominant poles of the original transfer function are copied in the reduced order transfer function), balanced truncation and optimal Hankel norm approximation (related to the controllability and observability Grammians of the transfer function [10]). These methods either provide a global error bound between the original and reduced-order system and/or guarantee stability of the reduced order system. Unfortunately, their exact calculation involves O(n3) floating point operations even for systems with sparse model matrices {A, B, C}, which becomes untractable for a very large state dimension n.

Only the image of the projecting matrices Z and V are important since choosing other bases satisfying the bi-orthogonality condition (2) amounts to a state-space transformation of the realization of

A more recent approach involves generalized Krylov spaces ([3]) which are defined as the images of the generalized Krylov matrices

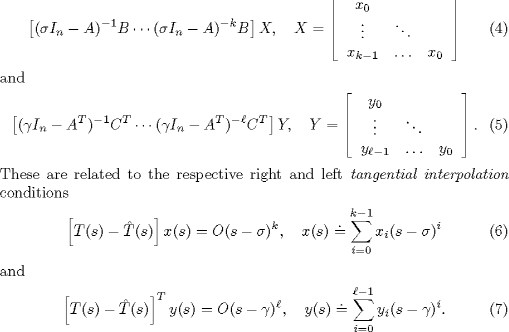
In the most general form, one imposes such conditions in several points and as well as bi-tangential conditions (see [2], [5] for more details). The calculation of Krylov spaces and the solution of the corresponding tangential interpolation problem typically exploits the sparsity or the structure of the model matrices (A, B, C) of the original system and are therefore efficient for large scale dynamical systems with such structure. Their drawbacks are that the resulting reduced order systems have no guaranteed error bound and that stability is not necessarily preserved.

The conjecture-and open problem-is that these methods are in fact quite universal (i.e., they contain the classical methods as special cases) and can be formulated in terms of Sylvester equations and generalized eigenvalue problems. Tangential interpolation would then be a unifying procedure to construct reduced-order transfer functions in which only the interpolation points and tangential conditions need to be specified.

3 OUR CONJECTURE

The error transfer function E(s) = T(s) - is realized by the following pencil:

The transmission zeros of the system matrix (i.e., the system zeros of its minimal part) can be chosen as interpolation points between T(s) and since the normal rank of E(s) drops below its normal rank. Therefore one can impose interpolation conditions of the type (6, 7) for appropriate choices of x(s) and y(s) and generalized eigenvalues and of (8).

Our conjecture tries to give necessary and sufficient conditions for this in terms of the system zero matrix.

Conjecture 2. A minimal state space realization of the strictly proper transfer function of McMillan degree k can be obtained by projection from a minimal state space realization of the strictly proper transfer function following equations

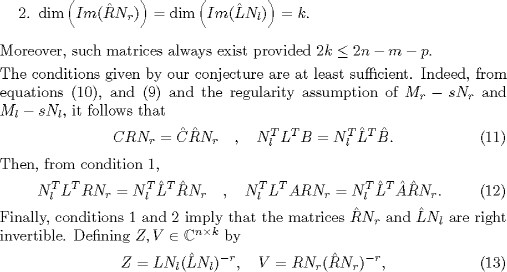
we can easily verify equations (1) and (2). Another justification is that (by looking carefully at the proof of theorem 1) Conjecture 3 is true for the SISO case.

We now present the link with the Krylov techniques. Equations (9) and (10) give us the following Sylvester equations:

In other words, our conjecture is that any projected reduced-order transfer function can be obtained by imposing some interpolation conditions or some modal approximation conditions with respect to the original transfer function. Moreover, a solution always exists provided 2k 2n - m - p (i.e., for all T(s) of sufficiently small degree k). If this turns out to be true, we could hope to find the interpolation conditions that yield, e.g., the optimal Hankel norm or optimal Hnorm reduced-order models using cheap interpolation techniques.

4 AVAILABLE RESULTS

Independently, Halevi recently proved in [6] new results concerning the general framework of model order reduction via projection. The unknowns

BIBLIOGRAPHY

[1] A. C. Antoulas, “Lectures on the approximation of large-scale dynamical systems, ” SIAM Book Series: Advances in Design and Control, 2002.

[2] J. A. Ball, I. Gohberg and L. Rodman, Interpolation of rational matrix functions, Birkhauser Verlag, Basel, 1990.

[3] K. Gallivan, A. Vandendorpe, and P. Van Dooren, “Model reduction via tangential interpolation, ” MTNS 2002 (15th Symp. on the Mathematical Theory of Networks and Systems), University of Notre Dame, South Bend, Indiana, USA, August 2002.

[4] K. Gallivan, A. Vandendorpe, and P. Van Dooren, “Model Reduction via truncation: an interpolation point of view, ” Linear Algebra Appl.

, submitted.

[5] K. Gallivan, A. Vandendorpe, and P. Van Dooren, “Model reduction of MIMO systems via tangential interpolation, ” Internal report, Universite catholique de Louvain , 2002. Available at http://www.auto.ucl.ac.be/ vandendorpe/.

[6] Y. Halevi, “On model order reduction via projection, ” 15th IFAC World Congress on automatic control, Barcelona, July 2002.

[7] J. J. Loiseau, S. Mondie, I. Zaballa and P. Zagalak, “Assigning the Kro-necker invariants of a matrix pencil by row or column completions, ”

Linear Algebra Appl., 278, pp. 327-336, 1998.

[8] E. Marques de Sá, “Imbedding conditions for -matrices, ” Linear Algebra Appl., 24, pp. 33-50, 1979.

[9] R. C. Thompson, “Interlacing Inequalities for Invariant Factors, ” Linear Algebra Appl., 24, pp. 1-31, 1979.

[10] K. Zhou, J. C. Doyle, and K. Glover, Robust and optimal control, Upper Saddle River, Prentice Hall, Inc, N.J.: 1996.