Problem 1.3

Does any analytic contractive

operator function on the polydisk

have a dissipative scattering

nD realization?

Dmitry S. Kalyuzhniy-Verbovetzky

Department of Mathematics

The Weizmann Institute of Science

Rehovot 76100

Israel

[email protected]

1 DESCRIPTION OF THE PROBLEM

It is known [5] that the transfer function of a dissipative scattering nD system belongs to the subclass of the class of all analytic contractive -valued functions on the open unit polydisk , which is segregated by the condition of vanishing of its functions at z = 0. The question whether the converse is true was implicitly asked in [5] and still has not been answered. Thus, we pose the following problem.

Problem: Either prove that an arbitrary can be realized as the transfer function of a dissipative scattering nD system of the form (1) with the input space and the output space , or give an example of a function (for some , and some finite-dimensional or infinite-dimensional separable Hilbert spaces that has no such a realization.

2 MOTIVATION AND HISTORY OF THE PROBLEM

For n = 1 the theory of dissipative (or passive, in other terminology) scattering linear systems is well developed (see, e.g., [2, 3]) and related to various problems of physics (in particular, scattering theory), stochastic processes, control theory, operator theory, and 1D complex analysis. It is well known (essentially, due to [8]) that the class of transfer functions of dissipative scattering 1D systems of the form (1) with the input space and the output space coincides with . Moreover, this class of transfer functions remains the same when one is restricted within the important special case of conservative scattering 1D systems, for which the system block matrix G is unitary, i.e., Let us note that in the case n = 1 a system (1) can be rewritten in an equivalent form (without a unit delay in output signal y) that is the standard form of a linear system, then a transfer function does not necessarily vanish at z = 0, and the class of transfer functions turns into the Schur class The classes and are canonically isomorphic due to the relation ).

coincides with the class of transfer functions of nD systems of Roesser type with the input space and the output space , and certain conservativity condition imposed. The analogous result is valid for conservative systems of the form (1). A system is called a conservative scattering nD system if for any the operator is unitary. Clearly, a conservative scattering system is a special case of a dissipative one. By [5], the class of transfer functions of conservative scattering nD systems coincides with the subclass , which is segregated from the latter by the condition of vanishing of its functions at z = 0. Since for n = 1 and n = 2 one has ), this gives the whole class of transfer functions of dissipative scattering nD systems of the form (1), and the solution to the problem formulated above for these two cases.

In [6] the dilation theory for nD systems of the form (1) was developed. It was proven that has a conservative dilation if and only if the corresponding linear function belongs to (. Systems that satisfy this criterion are called n-dissipative scattering ones. In the cases n = 1 and n = 2 the subclass of n-dissipative scattering systems coincides with the whole class of dissipative ones, and in the case n > 2 this subclass is proper. Since transfer functions of a system and of its dilation coincide, the class of transfer functions of n-dissipative scattering systems with the input space and the output space is 0n . According to [7], for any n > 2 there exist , operators and commuting contractions , . . . , n, such that

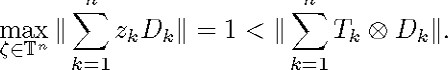
The syste is a dissipative scattering one, however not, n-dissipative. Its transfer function )

Since for functions in B0n (U, Y)S0n (U, Y) the realization technique elaborated in [1] and developed in [4] and [5] is not applicable, our problem is of current interest.

BIBLIOGRAPHY

[1] J. Agler, “On the representation of certain holomorphic functions defined on a polydisc, ” Topics in Operator Theory: Ernst D. Hellinger Memorial Volume (L. de Branges, I. Gohberg, and J. Rovnyak, Eds.), Oper. Theory Adv. Appl. 48, pp. 47-66 (1990).

[2] D. Z. Arov, “Passive linear steady-state dynamic systems, ” Sibirsk. Math. Zh. 20 (2), 211-228 (1979), (Russian).

[3] J. A. Ball and N. Cohen, “De Branges-Rovnyak operator models and systems theory: A survey, ” Topics in Matrix and Operator Theory (H.

Bart, I. Gohberg, and M.A. Kaashoek, eds.), Oper. Theory Adv. Appl., 50, pp. 93-136 (1991).

[4] J. A. Ball and T. Trent, “Unitary colligations, reproducing kernel hilbert spaces, and Nevanlinna-Pick interpolation in several variables, ”J. Funct. Anal. 157, pp. 1-61 (1998).

[5] D. S. Kalyuzhniy, “Multiparametric dissipative linear stationary dynamical scattering systems: Discrete case, ” J. Operator Theory, 43 (2), pp. 427-460 (2000).

[6] D. S. Kalyuzhniy, “Multiparametric dissipative linear stationary dynamical scattering systems: Discrete case, II: Existence of conservative dilations, ” Integr. Eq. Oper. Th., 36 (1), pp. 107-120 (2000).

[7] D. S. Kalyuzhniy, “On the von Neumann inequality for linear matrix functions of several variables, ” Mat. Zametki 64 (2), pp. 218-223 (1998), (Russian); translated in Math. Notes 64 (2), pp. 186-189 (1998).

[8] B. Sz.-Nagy and C. Foias, Harmonic Analysis of Operators on Hilbert Spaces, North Holland, Amsterdam, 1970.