Problem 10.4
Vector-valued quadratic forms in control
theory
Francesco Bullo
Coordinated Science Laboratory
University of Illinois
Urbana-Champaign, IL 61801
USA
Jorge Cortés
Coordinated Science Laboratory
University of Illinois
Urbana-Champaign, IL 61801
USA
Andrew D. Lewis
Mathematics & Statistics
Queen’s University
Kingston, ON K7L 3N6
Canada
Sonia Martínez
Matemática Aplicada IV
Universidad Politécnica de Cataluña
Barcelona, 08800
Spain
1 PROBLEM STATEMENT AND
HISTORICAL REMARKS
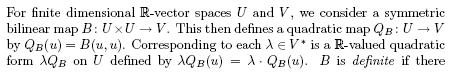
From the computational point of view, the first two questions are the more interesting ones. Both can be shown to be NP-complete, whereas the third one can be recast as a semidefinite programming problem.1 Actually, our main interest is in a geometric characterization of these problems. Section 4 below constitutes an initial attempt to unveil the essential geometry behind these questions. By understanding the geometry of the problem properly, one may be lead to simple characterizations like the one presented in Proposition 3, which turn out to be checkable in polynomial time for certain classes of quadratic mappings.
Before we comment on how our problem impinges on control theory, let us provide some historical context for it as a purely
mathematical one. The classification of 
-valued quadratic forms is well understood. However, for quadratic maps taking values in vector spaces of dimension two or
higher, the classification problem becomes more difficult. The theory can be thought of as beginning with the work of Kronecker,
who obtained a finite classification for pairs of symmetric matrices. For three or more symmetric matrices, that the classification
problem has an uncountable number of equivalence classes for a given dimension of the domain follows from the work of Kac
[12]. For quadratic forms, in a series of papers Dines (see [8] and references cited therein) investigated conditions when
a finite collection of -valued quadratic maps were simultaneously positive-definite. The study of vector-valued quadratic maps is ongoing. A recent
paper is [13], to which we refer for other references.
2 CONTROL THEORETIC MOTIVATION
Interestingly, and perhaps not obviously, vector-valued quadratic forms come up in a variety of places in control theory. We list a few of these here.
Local controllability: The use of vector-valued quadratic forms arises from the attempt to arrive at feedback-invariant conditions for controllability. Basto-Goncalves [6] gives a second-order sufficient condition for local controllability, one of whose hypotheses is that a certain vector-valued quadratic map be indefinite (although the condition is not stated in this way). This condition is somewhat refined in [11], and a necessary condition for local controllability is also given. Included in the hypotheses of the latter is the condition that a certain vector-valued quadratic map be definite.
Control design via power series methods and singular inversion:
Numerous control design problems can be tackled using power series and inversion methods. The early references [5, 9] show how to solve the optimal regulator problem and the recent work in [7] proposes local steering algorithms. These strong results apply to linearly controllable systems, and no general methods are yet available under only second-order sufficient controllability conditions. While for linearly controllable systems the classic inverse function theorem suffices, the key requirement for second-order controllable systems is the ability to check surjectivity and compute an inverse function for certain vector-valued quadratic forms.
Dynamic feedback linearisation: In [14] Sluis gives a necessary condition for the dynamic feedback linearization of a system
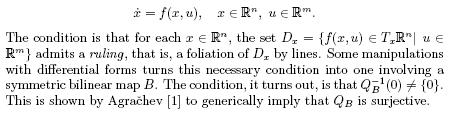
3 KNOWN RESULTS
Let us state a few results along the lines of our problem statement that are known to the authors. The first is readily shown
to be true (see [11] for the proof). If X is a topological space with subsets 
, we denote by intS(A) the interior of A relative to the induced topology on S. If S
V , aff(S) and conv(S) denote, respectively, the affine hull and the convex hull of S.
4 PROBLEM SIMPLIFICATION
This is, we think, a beautiful interpretation of the study of vector-valued quadratic mappings, and will surely be a useful formulation of the problem. For example, with it one easily proves the following result.
Proposition 3: If dim(U) = dim(V ) = 2 with B: U ×U
V a symmetric bilinear map, then 
is surjective if and only if B is indefinite.
BIBLIOGRAPHY
[1] A. A. Agračhe, “The topology of quadratic mappings and Hessians of smooth mappings, ” J. Soviet Math., 49(3):990–1013, 1990.
[2] A. A. Agračhev, “Quadratic mappings in geometric control theory, ” J. Soviet Math., 51(6):2667–2734, 1990.
[3] A. A. Agračhev and R. V. Gamkrelidze, “Quadratic mappings and vector functions: Euler characteristics of level sets, ” J. Soviet Math. , 55(4):1892–1928, 1991.
[4] A. A. Agračhev and A. V. Sarychev, “Abnormal sub-Riemannian geodesics: Morse index and rigidity, ” Ann. Inst. H. Poincaré. Anal. Non Lineaire, 13(6):635–690, 1996.
[5] È. G. Al’brekht, “On the optimal stabilization of nonlinear systems, ”J. Appl. Math. and Mech., 25:1254–1266, 1961.
[6] J. Basto-Goncalves, “Second-order conditions for local controllability, ” Systems Control Lett., 35(5):287–290, 1998.
[7] W. T. Cerven and F. Bullo, “Constructive controllability algorithms for motion planning and optimization, ” IEEE Trans Automat Control, Forethcoming.
[8] L. L. Dines, “On linear combinations of quadratic forms, ” Bull. Amer. Math. Soc. (N.S.), 49:388–393, 1943.
[9] A. Halme, “On the nonlinear regulator problem, ” J. Optim. Theory Appl., 16(3-4):255–275, 1975.
[10] J. Harris, Algebraic Geometry: A First Course, Number 133 in Graduate Texts in Mathematics, Springer-Verlag, New York Heidelberg Berlin, 1992.
[11] R. M. Hirschorn and A. D. Lewis, “Geometric local controllability: Second-order conditions, ” preprint, February 2002.
[12] V. G. Kac, “Root systems, representations of quivers and invariant theory, ” In: Invariant Theory, number 996 in Lecture Notes in Mathematics, pages 74–108, Springer-Verlag, New York-Heidelberg-Berlin, 1983.
[13] D. B. Leep and L. M. Schueller, “Classification of pairs of symmetric and alternating bilinear forms, ” Exposition. Math., 17(5):385–414, 1999.
[14] W. M. Sluis, “A necessary condition for dynamic feedback lineariza-tion, ” Systems Control Lett., 21(4):277–283, 1993.
1We thank an anonymous referee for these observations.