Problem 5.5

Exact controllability of the semi-linear

wave equation

Xu Zhang

Departamento de Matemática Aplicada

Universidad Complutense

28040 Madrid

Spainand

School of Mathematics

Sichuan University

Chengdu 610064

China

[email protected]

Enrique Zuazua

Departamento de Matemáticas, Facultad de Ciencias

Universidad Autónoma

28049 Madrid

Spain

[email protected]

1 DESCRIPTION OF THE PROBLEM

The exact (boundary) controllability problem of (1) can be formulated similarly. In that case, the control u enters on the system through the boundary conditions. This produces extra technical difficulties. The main open problem on the controllability of this semilinear wave equation we shall describe here arises in both cases. We prefer to present it in the case where the control acts on the internal subdomain to avoid unnecessary technical difficulties.

2 AVAILABLE RESULTS AND OPEN PROBLEMS

Nonlinearities with mild growth condition

Later on, based on a method due to Emanuilov ([5]), Cannarsa, Komornik, and Loreti ([2]) improved theorem 1 by relaxing the growth condition on f. The main result in [2] says that the same conclusion in theorem 1 holds if the condition (7) on f is replaced by (3). The growth condition (3) on f is sharp (since solutions of (1) may blow up whenever f grows faster than (3) at infinity and f has the bad sign).

For the higher dimensional case, Li and Zhang ([7]) proved the following result:

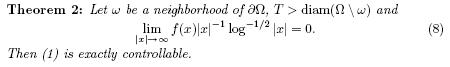
A special case of theorem 2 is when f is globally Lipschitz continuous, which gives the main result of Zuazua in [12]. The main result in [12] was generalized to an abstract setting by Lasiecka and Triggiani ([6]) using a global version of Inverse Function theorem and was extended in [9] to the case when T and satisfy the classical multiplier condition.

It is natural to conjecture that the same conclusion in Theorem 2 holds under the growth condition (3) on f as in one dimension. But this is by now an open problem. On the other hand, whether the same conclusion in theorem 2 holds for more general conditions on T and , say the classical multiplier condition or Geometric Control Condition, is also an open problem. Especially, when T and satisfy the Geometric Control Condition, the exact controllability problem for (1) is open even for globally Lipschitz continuous nonlinearities.

Nonlinearities with good sign and superlinear growth at infinity

In this case, there are no global exact controllability results in the literature. However, using a fixed point argument, Zuazua proved the following local exact controllability results for (1) ([10]):

Note that the controllability time T in theorem 4 depends on (y0, y1) and (z0, z1). According to [11], one can obtain explicit bounds on T. However, whether T may be chosen to be uniform, i.e., independent of the data (y0, y1) and (z0, z1), is an open problem even for the nonlinearity in (6) for n = 1.

This is certainly one of the main open problems in the context of controllability of nonlinear PDE.