Problem 10.3
Freeness of multiplicative matrix
semigroups
Vincent D. Blondel
Department of Mathematical Engineering
University of Louvain
Avenue Georges Lemaitre, 4
B-1348 Louvain-la-Neuve
Belgium
Julien Cassaigne
Institut de Mathématiques de Luminy
UPR 9016 - Campus de Luminy, Case 907
13288 Marseille Cedex 9
France
Juhani Karhumäki
Dept. of Math. & TUCS
University of Turku
FIN-20014 Turku
Finland
1 DESCRIPTION OF THE PROBLEM
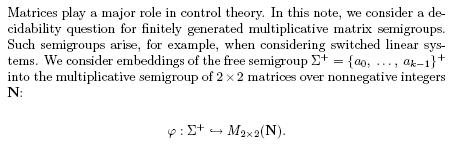

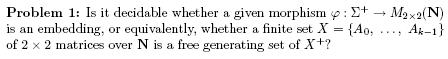
Problem 1 deserves two comments. First, we could consider matrices over rational numbers rather than nonnegative integers. This variant is -as it is not too difficult to see- equivalent to the case where matrices are integer matrices. Second, the problem is open even if only two matrices are considered:
Problem 2: Is it decidable whether the multiplicative semigroup generated by two 2 × 2 matrices over N is free?
Of course, the nontrivial part of problem 2 is the case when the semigroup is of rank 2. In many concrete examples, the freeness
is easy to conclude, as we saw. Amazingly, however, the problem remains even if the matrices are upper-triangular, as is ![]() above.
above.
2 MOTIVATION AND HISTORY
The importance of problem 1 should be obvious, without any further motivation. Indeed, product of matrices is one of the most fundamental operations in mathematics. In linear algebra it witnesses the composition of linear mappings, and in automata theory it defines the behavior of finite automaton, cf. [7], to mention just two examples. However, the importance of Problem 1 goes far beyond these general reasons.
The existence of embeddings like (2) have been known for a long time. Already in the 1920s J. Neilsen [12] was using these when studying free groups.
Such embeddings are extremely useful for both the theories involved. In one hand, these can be used to transfer results on words into those of matrices.
The undecidability is an example of a property that is natural and common in the theory of words, and translatable to matrices via these embeddings.
This, indeed, is essential in the spirit of this note.
On the other hand, there exist many deep results on matrices that have turned out useful for solving problems on words. A splendid example is Hilbert Bases Theorem, which implies -again via above embeddings- a fundamental compactness property of word equations, so-called Ehrenfeucht Compactness Property, cf. [5].
According to the knowledge of the author, the problems mentioned were first discussed in [10], where problem 1 was explicitly stated, and its variant for 3×3 matrices over N was shown to be undecidable. In [4] the undecidability was extended to upper-triangular 3 × 3 matrices over N, and moreover problem 2 was formulated.
Similar problems on matrices have been considered much earlier. Among the oldest results is a remarkable paper by M. Paterson [13], where he shows that it is undecidable whether the multiplicative semigroup generated by a finite set of 3 × 3 integer matrices contains the zero matrix. In other words, the mortality problem, cf. [16], for 3 × 3 integer matrices is undecidable.
According to the current knowledge, it remains undecidable even in the cases when a finite set consists of only seven 3×3 integer matrices or of only two 21 × 21 integer matrices, cf. [11] and [8, 3, 2]. For 2 × 2 matrices, the mortality problem is open.
The above undecidability results can be interpreted as follows. First, the existence of the zero element in a two generator
(matrix) semigroup is un-decidable, cf. [3]. Second, it is also undecidable whether some composition of an effectively given
finite set of linear transformation of Euclidian space ![]() equals to the zero mapping.
equals to the zero mapping.
The above motivates a related question: is it decidable whether a finitely generated semigroup contains the unit element? In terms of matrices, we state:
Problem 3: Is it decidable whether the multiplicative semigroup S generated by a finite set of n × n integer matrices contains the unit matrix?
For n = 2 this is shown to be decidable in the case of two matrices in [11], and in the case of an arbitrary number of matrices in [6], but in general the problem is open. A related problem, also open at the moment, asks whether the semigroup S contains a diagonal matrix. In this context, the following example is of interest.

3 AVAILABLE RESULTS


BIBLIOGRAPHY
[1] J. Berstel and D. Perrin, Theory of Codes, Academic Press, 1986.
[2] V. Blondel and J. Tsitsiklis, “When is a pair of matrices mortal, ” Inform. Process. Lett. 63, 283–286, 1997.
[3] J. Cassaigne and J. Karhumäki, “Examples of undecidable problems for 2-generator matrix semigroups, ” Theoret. Comput. Sci. 204, 29–34, 1998.
[4] J. Cassaigne, T. Harju and J. Karhumäki, “On the undecidability of freeness of matrix semigroups, ” Int. J. Algebra Comp. 9, 295–305, 1999.
[5] C. Choffrut and J. Karhumäki, “Combinatorics of words, ” In: G. Rozen-berg and A. Salomaa (eds.), Handbook of Formal Languages, vol. I, Springer, 1997, 329–438.
[6] C. Choffrut and J. Karhumäki, “On decision problems on integer matrices, ” manuscript.
[7] S. Eilenberg, Automata, Languages and Machines, vol. A, Academic Press, 1974.
[8] V. Halava and T. Harju, “Mortality in matrix semigroups, ” Amer. Math. Monthly 108, 649–653, 2001.
[9] T. Harju and J. Karhumäki, Morphisms, In: G. Rozenberg and A.
Salomaa (eds.), Handbook of Formal Languages, vol. I, Springer, 1997, 439–510.
[10] D. Klarner, J.-C. Birget and W. Satterfield, “On the undecidability of the freeness of integer matrix semigroups, ” Int. J. Algebra Comp. 1, 223–226, 1991.
[11] F. Mazoit, “Autour de quelques probl`emes ![]() de decidabilite sur des semi-groupes de matrices, ” manuscript, 1998.
de decidabilite sur des semi-groupes de matrices, ” manuscript, 1998.
[12] J. Nielsen, “Die Isomorphismengruppe der freien Gruppen, ” Math. Ann. 91, 169–209, 1924.
[13] M. Paterson, “Unsolvability in 3×3 matrices, ” Studies Appl. Math. 49, 105–107, 1970.
[14] E. Post, “A variant of recursively unsolvable problem, ” Bull. Amer. Math. Soc. 52, 264–268, 1949.
[15] W. Rytter, “The space complexity of the unique decipheribility problem, ” Inform. Process. Lett. 23, 1–3, 1986.
[16] P. Schultz, “Mortality of 2 × 2 matrices, ” Amer. Math. Monthly 84, 463–464, 1977.
