22
Digital Electronics
OBJECTIVES: After studying this chapter, you will be able to
- Explain binary, hexadecimal, and octal number systems
- Explain the practical importance of all those number systems
- Write decimal numbers in binary, octal, and hexadecimal systems and convert those to decimal numbers
- Define bit, byte, word, LSB, MSB, overflow, flag, microprocessor, and microcontroller
- Understand conversion from an analog measurement to a digital number
- Describe the relationship between precision in measurement and the number of bits of digital representation of the measured value
- Define and use DAC, ADC, A/D, and D/A
- Define signed and unsigned numbers and their application in measurement of physical systems
- Do basic arithmetic operations in binary numbers
- Describe one’s complement and two’s complement of binary numbers
- Give definitions for terms sampling, sampling time, and sampling rate
- Explain how an analog value is updated for being used in a computer-controlled device
- Understand a digital signal representation and a clock signal
- Understand how microprocessor control is performed in many small or large devices and equipment
- Define what binary-coded decimal is and what it is used for
New terms: Actuator, analog-to-digital converter, binary, binary-coded decimal (BCD), decimal system, digital-to-analog converter, falling edge, flag, hexadecimal, leading edge, least significant bit (LSB), microcontroller, microprocessor, most significant bit (MSB), negative going edge, one’s complement, over-flow, positive going edge, register, rising edge, rotation, sample and hold, sampling, sampling frequency, sampling rate, sampling time, shift right, signed number, trailing edge, two’s complement, unsigned number
22.1 Introduction
Many of the technological advancements we observe today, both at domestic level and industrial applications, are due to the progress in digital electronics. Examples are laptops, cellular phones, TV broadcasting, and many processes that are now controlled by a digital computer. In fact, all that started from a digital calculator leading to a digital computer (replacing an analog computer) and the rest.
Part of this technological advancement is due to progress in electronics, computer science, material science, miniaturization in manufacturing, and research and development on all the pertinent subjects. In this chapter and the next we cover the fundamentals of digital electronics without addressing the materials or the manufacturing processes. All digital electronics are based on a few analog devices that we have learned so far, on top of them the transistor. A computer chip, an integrated circuit that is made in a miniature scale and can be only 1.5 × 1.5 inch (4 cm × 4 cm), can contain 1 million components, most of them transistors.
22.2 Number Systems
The numbers we are familiar with and use every day are based on 10 symbols and rules for making and displaying all numbers, both positive and negative, from them. This system of numbers is the decimal system. We learned about most of these rules in elementary school. At this time these rules may look primitive, and we do not even think about them. But they are the same for other number systems used in digital computers that have revolutionized the world, which we will discuss in this chapter.
Decimal system: Most common numbering system with ten numbers (0 to 9) as the base for making all other numbers.
Note that in the decimal system the base is 10; we have 10 symbols, and the first number is 0. After counting to 9, the next number is composed of two digits: a 1 followed by the very first number, 0. Consider an ordinary number such as 543. Because we are used to ordinary numbers like 543, it is not necessary to indicate its base. Otherwise, we would have to write it as 54310, showing that its base is 10, or it is a number written in a decimal system.
In the rest of this chapter, unless it is required, we do not refer to a number as decimal or write it with the base. We follow the ordinary way of writing numbers.
The meaning of the number 543 is as follows:
543 = 5 × 100 + 4 × 10 + 3 × 1 = 5 × 102 + 4 × 101 + 3 × 100
(Remember that any number raised to power 0 is equal to 1.)
Also, note that any number multiplied by 10 receives an additional zero at its right, or if divided by 10 loses its rightmost digit (The rightmost digit is the least significant digit. We may need to round a number):
543 × 10 = 5430
543 ÷ 10 = 54 (+0.3)
All these and other rules are applicable to any other number system. We are going to see only 3 other number systems: hexadecimal, octal, and binary numbers. These are widely employed in the development or usage of industrial and domestic digital products. All that is done in calculators, computers, and the like are practically based on binary system, but for presentations, analysis, discussions, and theorem formulations, hexadecimal and octal systems are used. The reason for using hexadecimal and octal numbers is the convenience in converting from binary to those and vice versa. Conversion between decimal and binary numbers is not as convenient.
Hexadecimal: Numbering system with 16 as the base. Thus, there are 16 basic numbers (0 to 15) in order to make all other numbers. Furthermore, there are 16 symbols 10 of which are 0 to 9 and for the rest the capital letters A to F are used (A = 10, B = 11, C = 12, D = 13, E = 14, and F = 15).
Binary: Having two states: 0 and 1, true and false, high and low, on and off, yes and no.
22.2.1 Hexadecimal Number System
Hexadecimal represents a number system whose base is 16 (made out of the Greek word hex for 6 and decimal denoting association with 10). Initially, therefore, 16 symbols are necessary to represent all numbers. Also, in writing hexadecimal numbers it is necessary to somehow indicate that its base is 16 and not 10.
The 16 numbers for the base of the hexadecimal system are numbers 0 to 15. For numbers 0 to 9 the same symbols used in the decimal system are employed. For numbers 10 to 15 the letters A to F are utilized, without any name. The base for hexadecimal system is then
0 1 2 3 4 5 6 7 8 9 A B C D E F
and their corresponding decimal values are
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
The following number after F in hexadecimal system is 10, in the same way that in decimal numbers after 9 we have 10. To show that a number is written in the hexadecimal system (or its base is 16), we can put the base as a subscript for the number, like 54316. A more common way is to put an X before the number (e.g., X543) or add an H after the number, like 543H. Thus,
X543 = 54316 = 543H = 5 × 162 + 4 × 161 16 + 3 × 160 = (5)(256) + (4)(16) + (3)(1) = 1347
The following shows examples of hexadecimal numbers (without the preceding X):
48, 312, A9, C3, 2AA, ABCD, 3FF, 6A2B, 12DF
To have a better feeling for the values of these numbers, we calculate their decimal equivalents. You notice that if we do not use the preceding X, it is not clear if numbers such as 48 and 312 are decimal or hexadecimal, and these are quite different. The decimal magnitudes of hexadecimal numbers are calculated in the same way shown earlier for 543 in both cases of having 10 or 16 as for base. Because 160 = 1, we refrain from its repetition and use 1 for the multiplier of the rightmost (least significant) digit.
X48 = 4 × 161 + 8 × 1 = 72
X312 = 3 × 162 + 1 × 161 + 2 × 1 = 786
XA9 = 10 × 161 + 9 × 1 = 169
XC3 = 12 × 161 + 3 × 1 = 195
X2AA = 2 × 162 + 10 × 161 + 10 × 1 = 682
XABCD = 10 × 163 + 11 × 162 + 12 × 161 + 13 × 1 = 43,981
X3FF = 3 × 162 + 15 × 161 + 15 × 1 = 1023
X6A2B = 6 × 163 + 10 × 162 + 2 × 161 + 11 × 1 = 27,179
X12DF = 1 × 163 + 2 × 162 + 13 × 161 + 15 × 1 = 4831
X99 = 9 × 161 + 9 × 1 = 153
XFF = 15 × 161 + 15 × 1 = 255
X100 = 1 × 162 + 0 × 161 + 0 × 1 = 256
XFF + 1 = X100
Note that equivalent to 99, 999, and similar decimal numbers (i.e., those figures before the number of digits increases) in hexadecimal system we have FF, FFF, and so on. Thus,
X1000 − 1 = XFFF
XFFFF + 1 = X10’000
(Note that it is not necessary to write X1 instead of 1 because there is no ambiguity.)
Example 22.1
Find the decimal equivalent of XABCD0.
Solution
In the same way that in the decimal number system a number like 1230 is 10 times the number 123, we can use the analogy to say the number XABCD0 is 16 times the number XABCD. The decimal equivalent of the latter has already been found to be 43,981. Thus, for the decimal value of XABCD0, we have
XABCD0 = (16)(43,981) = 703,696
The reverse process of finding the hexadecimal expression of decimal numbers can be done by successive divisions by 16. The remainder of a division determines the digit for the number. Consider, for example, the small figure 23. Dividing this figure by 16, we can write

The arrows on the left show the procedure, and the arrows on the right show the answer. The answer is 17, as defined by the numbers 7 and 1 denoted by arrows. The oblique arrow starting from 1 on the first row toward the second row denotes the transfer of the quotient to a new line for continuation of the same process of dividing by 16. The vertical arrow shows that when the quotient becomes 0 the process should stop.
For this small number, only one division is sufficient (the last one is not really necessary). But for larger numbers the dividing process must be repeated a number of times until no more division is possible (or no extra results are obtained). The following examples show the same procedure for larger numbers. It is not necessary to show the arrows. Here they help understanding.
Example 22.2
Find the hexadecimal representation of 2002.
Solution
We carry out dividing by 16 showing the process in the same format as above.

The corresponding hexadecimal number, therefore, is X7D2 (D is for the decimal 13).
Example 22.3
Find the hexadecimal representation of decimal 52,778.
Solution
52,778 = 3298 ´ 16 + 10 → A
3298 = 206 ´ 16 + 2 → 2
206 = 12 ´ 16 + 14 → EE
12 = 0 ´ 16 + 12 → C
The answer is XCE2A.
22.2.2 Binary Number System
The binary number system has only two base numbers, 0 and 1. The reason for developing such a number system is its applicability to many physical processes that have two states, and thus a binary number is sufficient to describe them. These physical states can be in the form of
- On and off
- True and false
- High and low
- Yes and no
- Positive and negative
depending on the application. For example, for switches and switching devices in an electrical circuit the on-off defines the state of one switch. This can be the basis of storing data, which can consist of the many switches or devices where each one assumes one of the two states at a time.
A number in the binary system, thus, can have only 0’s and 1’s because there is no other symbol. Note that in the same way that in the decimal system the number after 9 (the last number element) is 10, in the binary system the number after 1 is 10. The following lines show a few examples of some decimal numbers when written in the binary system. A subscript b or 2 is used to indicate that a number is binary.
0 = 0
1 = 1
2 = 10b
3 = 11b
4 = 100b
10 = 1010b
11 = 1011b
12 = 1100b
15 = 1111b
16 = 10000b
Before we learn how to find the binary equivalent of a number, note that in the same way that 10 + 1 = 11, in the given binary numbers the same thing can be verified:
1010b + 1 = 1011b
and after 1111b (the last four digit binary number) is 10000 (the first five-digit number), in the same way that after 9999 in decimal numbers we have 10000.
The decimal equivalent of any binary number can be found by the same procedure we have used earlier for the number 543. We use the above figures to verify that they really are equivalent to each other:
10b= 1×21 + 0 ×20 = 2 + 0 = 2
11b= 1×21 +1×20 = 2 +1 = 3
1111b= 1×233 +1×22 +1×21 +1×20 = 8 + 4 + 2 +1 = 15
10000b= 1×24 + 0 ×23 + 0 ×222 + 0 ×21 + 0 ×20 = 16 + 0 + 0 + 0 + 0 = 16
Example 22.4
Find the decimal number for the binary 1011010110b.
For clarity, it is convenient to show the number as 10,1101,0110b, that is, separating each four digits from right. This number has 10 digits.
1 × 29 + 0 × 28 + 1 × 27 + 1 × 26 + 0 × 25 + 1 × 24 + 0 × 23 + 1 × 22 + 1 × 21 + 0 × 20 = 512 + 128 + 64 + 16 + 4 + 2 = 726
But, note that it is not necessary to write the multipliers because they are either 1 or 0. Moreover, 0 multiplied by any number results in 0; hence, it is not necessary to write. The above mathematical line can be reduced to
29 + 27 + 26 + 24 + 22 + 21 = 512 + 128 + 64 + 16 + 4 + 2 = 726
To find the binary number equivalent of a decimal number, use the following procedure:
- Divide the number by 2 and write the quotient and the remainder.
- If the remainder is 0, the rightmost digit is zero; otherwise, it is 1.
- Substitute the quotient for the number and repeat the division by 2.
- If the remainder is 0, the second digit is 0; otherwise, it is 1.
- Continue the same procedure until the quotient reaches 0.
The following example shows this procedure.
Example 22.5
Find the binary equivalent number for 86.
Solution
The sequence of divisions by 2 can be arranged in the following format:

The binary representation of 86, thus, is 1010110.
22.2.3 Octal Number System
Another number system that is more utilized in industry is the octal numbers, having number 8 as the base. The rules for conversion from octal to decimal and vice versa are the same as the other number systems. Numbers 0 to 7 are used for the eight main symbols. Thus, the positive numbers start from 0 and are
0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20 …
Again, each octal number must be followed by a subscript 8 to indicate its base. The following examples show calculation of the decimal equivalent of an octal number and the octal equivalent of a decimal number.
Example 22.6
Find the decimal value of 20128.
Solution
20128 = 2 × 83 + 0 × 82 + 1 × 81 + 2 × 1 = 2 × 512 + 8 + 2 = 1034
Example 22.7
Find the octal representation of number 7777.
Solution
| 7777 = 972 × 8 + 1 | → | 1 | first digit from right |
| 972 = 121 × 8 + 4 | → | 4 | second digit |
| 121 = 15 × 8 + 1 | → | 1 | third digit |
| 15 = 1 × 8 + 7 | → | 7 | fourth digit |
| 1 = 0 × 8 + 1 | → | 1 | fifth digit |
The octal number is 171418.
22.2.4 Conversion between Binary and Hexadecimal Numbers
The fact that hexadecimal numbers are based on 16, and 16 is the fourth power of 2 makes the conversion between hexadecimal and binary numbers easy. Consider a single digit hexadecimal number. The values expressed by this digit are between 0 and 15. Now consider the numbers that may be represented by four digits in a binary number. Again, they are between 0 and 15. All these numbers are compared together below (the prefix X for hexadecimal numbers is omitted for simplicity).
0001b=1
0010b=2
0011b=3
0100b=4
0101b=5
0110b=6
0111b=7
1000b=8
1001b=9
1010b=A
1011b=B
1100b=C
11001b=D
1110b=E
1111b=F
The above equivalence can be directly carried to all other digits of a hexadecimal number and the set of four digits of a binary number. The following are some examples.
X123 = 0001,0010,0011b
X47A = 0100,0111,1010b
XBCD1 = 1011,1100,1101,0001b
XA00F5 = 1010,0000,0000,1111,0101b
1111,1100,0011,0000,1110 = XFC30E
0000,1001,0000,1111 = X90F
Note that in the last number the leftmost 0 is not shown in the hexadecimal number, whereas in a binary number it is very common to have 0’s on the left, as you will see in the next section.
Example 22.8
Find the hexagonal equivalent of 1001,1010,1100,1111,1000, 0001.
Solution
Each digit can be calculated or looked up in the preceding list. Thus,
1001,1010,1100,1111,1000,0001 = 9ACF8116
22.2.5 Direct Conversion between Binary and Octal Numbers
On the basis of the discussion in Section 22.2.4, a direct conversion between octal and binary numbers is possible. A binary number can be divided in groups of three, each of which corresponds to one digit of its associated octal number. Only the first 8 out of 16 in the preceding list correspond to octal numbers, and the 0 on the left must be omitted so that there are only three digits for each binary number. Some examples are as follows.
000,101,000,100b = 5048
000,101,111,100b = 5748
001,001,111,101b = 11758
010,111,110,000b = 27608
100,111,110,000b = 47608
111,101,011,001b = 75318
As said before, the 0’s on the left side of a binary number do not need to be included in the converted number.
22.3 Number Conversion and Precision
Most of the physical parameters that we deal with every day have an analog nature, such as temperature, wind speed, line voltage, pressure in a tube, flow rate in a pipe, sun’s position with respect to a solar farm, angle of a solar panel, and so forth. For using a computer or a microprocessor for measurement and control, and for other purposes such as display and data storage, their values can be converted to digital numbers. This is carried out through converters. These converters must not be confused with power converters that we have studied before.
Microprocessor: Integrated circuit for all arithmetic and logic operations in a computer.
For altering the physical values that come out of measurements to the form that can be used by a microprocessor an analog-to-digital converter (ADC) is used. Also, for the reverse action a digital-to-analog converter (DAC) is employed. The latter is used to send an analogue value to an actuator, for instance. An actuator is any device that acts on a mechanical system, for example, a motor or hydraulic piston that turns the blades of a wind turbine to a desired pitch angle, or the adjusts the angle of a solar panel toward the sun’s rays. The desired angle is obtained from some calculations that the system microprocessor performs.
Analog-to-digital converter: Electronic device that generates a digital signal from an analog signal so that the signal can be treated with digital devices. This is normally used for measured values. In such a case converted signals must be updated at a desired frequency.
Digital-to-analog converter: Electronic device that translates the value of a digital signal generated by a computer or a digital device into an analog value that can be used in an electric circuit.
Actuator: Any physical device that can generate a mechanical action (e.g., rotation, force exertion, moving) based on an electric, hydraulic, or pneumatic excitation.
A microprocessor is the brain of a computer that controls all the numerical operations and peripheral actions of the computer. It is not necessarily used only in a computer. There are special purpose microprocessors for specific purposes. Also, in many devices, microprocessors are employed for adjusting the performance of the device based on given conditions and desired objectives. Examples can vary from a huge turbine to a camera, a car, a washing machine, a coffeemaker, and many more. For each purpose an appropriate microprocessor is used. Figure 22.1 illustrates the schematic of what happens in any microprocessor controlled device. In this figure, A/D and D/A stand for analog-to-digital (ADC) and digital-to-analog (DAC) converter, respectively. For control systems a small microprocessor, specifically designed for control purposes, built together with other necessary components such as memory and input/output devices, is referred to as a microcontroller.
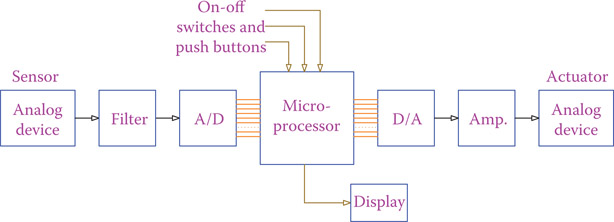
Figure 22.1
Schematic of a microprocessor control system.
Microcontroller: A one chip integrated circuit (IC) comprising a main processor plus all components and input/output terminals that can be used for control purposes (process control and control of machinery).
In Figure 22.1, you can see that output of a measurement device may need to be filtered for noise and unwanted signals. Also, the output from a microprocessor may be too weak to be able to drive a system. Thus, an amplifier is used to amplify the signal.
Not all the inputs to a microprocessor (or microcontroller) are initialized from a parameter with an analogue quantity. Certain measurements are naturally in a binary form and can be readily used. The output of a switch in most cases is on and off, which is already in the binary form. These parameters do not need any conversion. A switch is either on or off, a key is either pressed or not pressed and a pushbutton either is or is not pushed. Binary numbers serve as the best way to show these on and off states because the associated data can be easily stored and accessed in the form of 0’s and 1’s.
The best example for conversion from analog to digital is a digital watch in which the time, an analog quantity, is converted to a digital variable and is digitally displayed. Certain variables have a digital nature, such as the number of people entering a library, or the number of cars crossing a bridge. In fact, anything that can be counted, has a digital nature and anything that can be measured has an analog nature.
No matter if the numbers correspond to an analog quantity, come directly from a digital counter, or are already in a binary form, binary numbers must be used for their processing. Processing implies measuring, recording, performing arithmetic operations on numbers, displaying numbers, and similar actions that are performed by a digital computer. For recording and storing binary numbers, at the base level, an electronic device is used that is capable of holding a value of 0 or 1. For example, a charged capacitor can represent 1 and a discharged capacitor 0. This is for a single one digit binary number.
For larger numbers, more than one unit of the 0 and 1 storing device is essential. Then the size of the physical device in terms of how many 0’s and 1’s can be allocated for a number becomes important.
22.3.1 Bits and Bytes
In dealing with binary numbers, the terms bit and byte come into picture. A bit is the unit for the digits that a binary number can have. Thus, the smallest binary number has 1 bit, and its value can be 0 or 1. A byte is a group of 8 bits together. The memory and the digital processor for many devices may contain 8 bits (one byte), but computers have larger number of bits for their number processing. Today’s laptops are made with 32-bit or 64-bit processors and the larger computers can be based on 128 bits. This number of bits is for representing or storing one digital number, only. A computer can handle millions of numbers. Thus, it has many units of the 128-bit device. This defines the computer memory, which is normally measured in bytes; for example, 32 megabytes or 4 gigabytes, etc. Associated with bit and byte in computer terminology a word is a group of 16 bits or two bytes.

Figure 22.2
Representation of bits, bit numbers, and their values.
Figure 22.2 shows the representation of the electronic circuits that hold binary numbers. We refer to this electronic device as a register. At this time we are only concerned about the bits and bytes, without caring about what circuits constitute the register. When there are a number of bits, like in a byte, the rightmost bit is called the least significant bit (LSB), and the leftmost bit is called the most significant bit (MSB). Each bit is numbered for ease of reference. The rightmost bit is bit 0, followed by bit 1, bit 2 and so forth. The last bit in a byte, therefore, is bit 7. There is a value associated with each bit. This value is obtained by raising “2” to the power defined by the bit number. For instance, the first one from the right has a value 20 = 1, and the most significant figure in a byte has a value of 27 = 128. These numbers are also shown in Figure 22.2 for a byte.
Register: Electronic device to store digital data (in the form of binary numbers), made of a number of flipflops, one for each bit.
Least significant bit (LSB): The bit on the far right in a binary number.
Most significant bit (MSB): Leftmost bit in a binary number.
As can be understood, with 4 bits only, the smallest number that can be addressed or stored is zero, when all bits are 0, and the largest number is 15, when all bits are 1. Altogether, 16 values can be recorded. Similarly, with 8 bits, the smallest number is zero and the largest number is 255. This implies that only 256 values are possible. These are 255 positive integer values plus zero.
Example 22.9
Determine with 64 bits how many numbers can be stored.
The smallest number (negative numbers are not yet considered) is 0, when all bits are 0. The problem is finding the number when all bits are 1. We can use the same procedure used to find the decimal equivalent of a binary number, that is,
11…11b = 1 × 263 + 1 × 262 + … + 1 × 21 + 1 × 20
But, this is tedious and time-consuming. Consider what was said earlier about 1111b and 10000b. That is, the number with all bits equal to 1 is one less than the next number with only the most significant bit being 1 and all the other bits being 0.
Thus, we have
11…11 = 1 × 264 b – 1 = 18446744073709551616 – 1 = 18,446,744,073,709,551,615
You may ask where such a large number is used. Remember that negative and fractional numbers need to be handled, too. Computers use 64 bits, but for industrial use sometimes even 4 bits may suffice for very simple applications.
In practice, we often have negative values, particularly in measurements. We continue this discussion to see how negative binary numbers can be stored. For dealing with negative binary numbers it is crucial to adopt a fixed number of bits. If not, numbers cannot be interpreted correctly. Normally, a commercial device comes with a fixed bit size, and the greater the number of bits, the more expensive the device is.
22.3.2 Representation of Negative Binary Numbers
For simplicity and better clarity, in what follows only 8 bits are used. With 8 bits the total numbers that can be addressed is limited. Dealing with larger numbers requires larger bit size. Nevertheless, in many small applications, 8 bits is sufficient.
When an 8-bit device is in use we need to fill all the places in the register with 0’s and 1’s. In other words, for each bit a value must be defined and it cannot be left without a value. For instance, for storing the decimal number 86 in a binary form it was found that (see Section 22.2) 86 = 1010110b. This number has only 7 digits and occupies 7 bits in a register. To represent this number with 8 bits the remaining bit on the left is filled with a 0 and thus 86 is represented by 0101,0110b. For any other number in the same way all remaining bits from left are filled with 0’s.
In computer terminology, positive numbers are referred to as unsigned numbers, and when we have both positive and negative numbers, then we need to use signed numbers. With 8 bits there are 256 possible numbers. For any application an initial decision must be made if these 256 possibilities are to be used for the range of 0 to 255 unsigned numbers, or half are negative and half positive and, therefore, the 256 positions must accommodate 256 signed numbers.
Unsigned number: Binary number representing a positive value, as opposed to a signed number, which can represent a positive or negative value.
Signed number: Binary number that can be positive or negative. Sign (of the number) must be embedded with the bits representing the number.

Figure 22.3
Signed and unsigned 8-bit numbers.
In unsigned numbers (for 8 bits) the most significant bit has a value of 27 = 128, whereas in signed numbers this bit represents the negative sign. Figure 22.3 shows this fact. The unsigned numbers start from 0 and end with 255, and are as follows:
0000,0000 = 0
0000,0001 = 1
0000,0010 = 2
…
1111,1110 = 254
11111,1111 = 225
and the signed numbers are from −128 to +127, as follows:
1000,0000 = −128
1000,0001 = −127
1000,0010 = −126
…
1111,,1111 = −1
0000,0000 = 0
0000,0001 = +1
…
0111,1111 = +127
Below we see some examples of signed numbers. Pay attention to the fact that if a positive number and a negative number of the same quantity are added, the resultant is zero. Note and compare the numbers having similar bits except for the most significant bit.
Unsigned:
0000,1100 = 12
0010,1100 = 44 (32 + 12)
0110,1100 = 108 (64 + 44)
1111,1111 = 255
Signed:
0010,1100 = 44 (same as above)
0110,1100 = 108 (same as above)
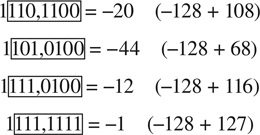
Although a way to find the value of a negative number is shown above (in the brackets), this is not the best way. Also, we want to find the negative of a given number. There is a rule for finding the negative of a binary number. This is discussed under one’s and two’s complement in Section 22.4.
22.3.3 Precision in Analog-to-Digital Conversion
Today, in many industries, microprocessors are used for control of processes and plants. Examples of that are plenty. Today’s cars are equipped with a microprocessor that controls the performance of the engine by measuring a number of parameters, such as air temperature, car speed, position of the gas pedal, and other pertinent parameters. Likewise, the operation of a wind turbine, steam turbine, and gas turbine is supervised and controlled by a microprocessor based on many parameters that need to be measured.
A microprocessor is the brain of any computer and any equipment with digital control. There are many different microprocessors with different bit size and different capabilities. In all microprocessor-based control systems, when an analog quantity is measured, it must be converted to its digital equivalent, so that it can be read or stored digitally or better, say, by a binary number.
The output of most measurement devices is in the form of a voltage. For some variables like wind speed this value is always positive (we do not have negative wind speed) and for some other ones, like temperature this can be positive or negative. According to what was said before, a signed or unsigned number can be decided on based on the requirement.
Suppose that the output of a measurement device is a voltage that can vary between 0 and 10 V. Considering an 8-bit converter, there are 256 possibilities for the values that can be recorded, processed, and displayed. In this case the 256 numbers correspond to 10 V range. Because there are 255 intervals (between 0 and 255), each digital number corresponds to 10/255 V, which is approximately 0.039 V. This implies that within the converted digital values the difference between any number and the number next to it is 0.039 V. This value of 0.039 V is the resolution of the representation of 10 V by 8 bits. It determines the precision of the operation. Samples of the binary values and their corresponding voltages for this example are shown below:
| 0000,0000 | 0V | |
| 0000,0001 | 0.039V | (1 × 0.039) |
| 0000,0011 | 0.117V | (3 × 0.039) |
| 0011,1100 | 1.95V | (50 × 0.039) |
| 1000,0000 | 5.0V | (128 × 0.039) |
The above numbers show that the difference between any two consecutive numbers that can be displayed through a digital display is 0.039 V. For instance, considering the two first numbers, a measured value can be 0 or 0.039 V, and nothing in between. With 8 bits it is not possible to have a better precision. To have a higher precision, either the voltage range must be smaller or the number of bits (bit size) must be increased, as shown in the following examples.
Example 22.10
Determine how much is the precision in the conversion of 5 V range by an 8-bit system.
Solution
Divide the 5 V range by 255 possible graduations.
5 V ÷ 255 = 0.0196 V = 19.6 mV
The precision in this case is twice that of the previous case.
In analog-to-digital conversion the higher the number of bits, the higher the precision of conversion.
Example 22.11
Determine the precision if a 10-bit converter is used for conversion of numbers between −5 and +5 V.
Solution
With 10 bits the possible number of binary values is 210 = 1024 (0 to 1023); that is, 4 times more than with 8 bits. Also, note that for the range of values between −5 and +5 V, we have 10 V.
Following the same procedure as in the previous example, we come up with
10 ÷ 1023 = 0.00977 V = 9.77 mV
Note that for this example it is necessary to use signed numbers to be able to accommodate and display the negative values.
Precision determines the maximum error that can exist due to conversion to digital values. Only those values that are a multiplier of 0.00977 can be represented by their real value. For other numbers, there exists an error. For instance, consider the real value of a voltage to be 2 V. Also, consider the following binary numbers and their corresponding decimal values
00,1100,1100b(204) → 204 ´ 0.00977 = 1.99308
00,1100,11101b(205) → 205 ´ 0.00977 = 2.00285
00,1100,1110b(206)) → 206 ´ 0.00977 = 2.01262
The nearest binary number corresponding to 2 V is the middle one, 00,1100,1101b but is not exact (the exact value is 204.8 × 0.00977, which cannot be addressed by a binary number here). The error in this case is 0.00285 V (2.85 mV); the error may be larger than this, but not greater than 9.77 mV.
Conversion from analog to digital values contains inevitable error. Only some of the digital values that will be displayed represent the true measured value without error.
22.4 One’s and Two’s Complement
For the analysis of practical applications it is necessary to do mathematical operations on binary numbers. This is the basis of all that a microprocessor does. In this section we study how two binary numbers are added, how one is subtracted from the other. We also discuss how the negative of a binary number is formed.
22.4.1 Addition
The addition of two binary numbers is performed in the same way as we add two decimal numbers with the exception that the only nonzero element in the set of basic elements of the binary number system is the number 1. Thus, in the same way that in decimal numbers if we add 1 to 9, the answer is 10, in binary numbers if we add 1 to 1, the answer is 10. That is, the addition of 1 and 1 is a 0 with a 1 carried over to the next digit on the left. Also, practically, which is the way this operation is performed in microprocessors, only two numbers are added together at a time. We consider the following three examples. Assume unsigned numbers.
| 10100011+ | 10100011+ | 01010101+ |
| 00101010 |
10100011 |
11111110 |
| 11001101 | 101000110 | 101010011 |
Because any binary numbers is practically the contents of a register, only a limited number of bits are available. This is because of the hardware, which determines the bit size to be 8, 10, 12, or some other. In the result of adding two numbers you see that the very last digit on the left is shown in red, when it happens to exist. This digit (bit) is ignored. There is physically no place for this bit to go to. It is either not significant (in a subtraction operation, as you will see next), or it is an indication of overflow (as shown above). Overflow is a situation where a number is larger than the capacity of the machine. When there is an overflow situation, the last bit is ignored, but it signals out a flag. A flag is an indicator of an undesirable or fault situation in digital systems. A message will be issued when a flag is signaled. An example is when you have a division by zero in your calculator.
Overflow: State of reaching a value beyond the capacity of a digital device in terms of the number of bits.
Flag: Representation of the occurrence of of some unusual or unwanted situation in digital circuits and computer terminology.
22.4.2 Subtraction
To subtract a number B from number A the common method is to add A to the negative of B.
A − B = A + (−B)
The subtraction, then, changes to an addition operation. Then, in the same way as discussed above the two numbers are added.
Consider for example subtraction of 44 (0010,1100b) from 108 (0110,1100b) in binary operation. Instead, we add −44 (1101,0100b) to 108
01101100 +
11010100
101000000
You can easily check that 108 − 44 = 64, and the resultant binary number (0100,0000b) is 64. Also, you can verify the number for −44 to be correct. If it is added to 44, the resultant is 0.
01101100 + (44)
11010100 (–44)
100000000
Note that in both cases the very last digit, shown in red, does not play any role and is ignored.
22.4.3 One’s Complement of a Binary Number
The one’s complement of a binary number is used to find the two’s complement of a number, which is used to find the negative of that number. Note that negatives are valid with signed numbers. The one’s complement of a number is obtained by switching each bit to its opposite value, 1’s to 0’s and 0’s to 1’s. For example, the one’s complement of 0110,1010 (106) is 1001,0101.
One’s complement: Result of swapping each bit value to its complement in a binary number.
Two’s complement:
A binary number obtained by adding 1 to the one’s complement of a binary number.
22.4.4 Two’s Complement of a Binary Number
Two’s complement of a binary number is obtained by adding 1 to the one’s complement of that number. For instance,
| if one’s complement of a number is then the two’s complement of it is | 10010101 |
| 10010101+ | |
| 1 |
|
| 10010110 |
The two’s complement defines the negative of a number. Therefore, the negative of 0110,1010b is 1001,0110b. We can check this by adding the two numbers together.
01101010+
10010110
100000000
Example 22.12
Find the negative of the signed binary number 1110,0111.
Solution
First, note that this number is already negative because its most significant bit is 1. The negative of a negative number is positive. No matter if the number is initially positive or negative, the two steps to be taken are
- Step 1. Find the one’s complement of the number One’s complement of 1110,0111 is 0001,1000.
- Step 2. Find the two’s complement of the number (or, add 1 to the one’s complement)
0001,1000b + 1 = 0001,1001b
The answer, thus, is 0001,1001.
Verifying the result:
11100111+
00011001
100000000
The given numbers was −25. You cannot say that easily just from the number directly by looking at the digits, except that one has a look-up table showing all the numbers in the range. Figure 22.4 shows some numbers between −128 and −1. You may notice a pattern to determine the numbers for 8 bits as shown in the table. On the basis of this pattern, find the decimal magnitude of the binary number leaving out the leftmost bit, and subtract 128 from that number. For other bit numbers the value to subtract (128 in this case) must be changed accordingly.
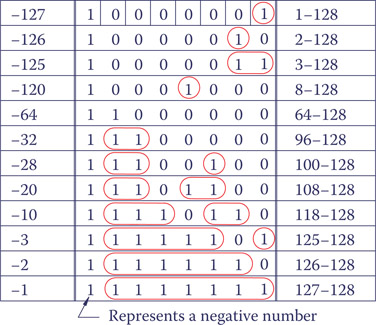
Figure 22.4
Negative binary numbers.
The two’s complement of a binary number defines the negative of that number.
22.4.5 Multiplication and Division of Unsigned Binary Numbers
Multiplication of binary numbers is very easy. This is the way multiplication is performed in a microprocessor. First, consider multiplication by 10b and 100b, which is, in fact, multiplication by 2 and 4. Consider 0011,1011b (always assume a limited number of bits, here 8). Assume an unsigned number.
| 0011,1011b × 10b = 0111,0110b | (592 × = 118) |
| 0011,1011b × 100b = 1110,1100b | (594 × = 236) |
As in the case of decimal numbers 1 or 2, 0’s are added to the right side of the number for multiplication by 10b and 100b, respectively. Because the number of bits must remain the same, this operation is like bringing the 0’s from the left hand to the right hand. Figure 22.5 depicts this. This operation of moving 0’s to the right is called rotation.
Rotation: (in binary number operations) Operation of moving one or more leftmost zeros in a binary number with a limited number of digits to the far right. This implies multiplying that number by 10b, 100b, etc.
Rotation to the right is performed for multiplication, 1 bit for multiplication by 10b, 2 bits for multiplication by 100b, and so on. Note that here if multiplication is continued, then eventually overflow happens when the result becomes larger than a machine can handle (here because there are only 8 bits, not many numbers can be handled, but in a machine with 128 bits the operation can go on much further).
For multiplication by numbers like 3 (11b) and 6 (110b) and so forth, these numbers are broken into their components. For example,
11b = 10b + 1
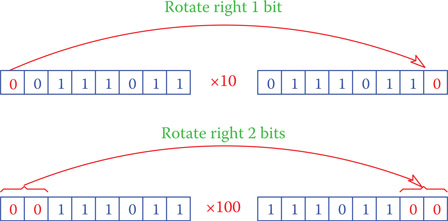
Figure 22.5
Multiplication of a number by 10b and 100b.
Thus, multiplication of a binary number by 11b includes multiplication of that number by 10b, as above, and multiplication of the number by 1(multiplication by 1 is trivial and does not change the number), and adding the results. Similarly, multiplication by 110b includes multiplication by 100b plus multiplication by 10b,
110b = 100b + 10b
both of which we have already seen. The results of the two multiplications then must be added together. Multiplication by all other numbers can be treated the same way.
Example 22.13
Multiply the 10-bit binary number 00,0110,0111b by 7.
Solution
Multiplication of the number by 7 consists of multiplication by 4 + 2 + 1. Because 7 = 111b, then the number must be multiplied by 100b, multiplied by 10b, and multiplied by 1b followed by adding all the results.
00,0110,0111b´ 100b= 01,1001,1100b
00,0110,0111b´ 100b= 00,1100,1110b
00,0110,0111b´ 1b= 00,0110,0111b
The final result is
01,1001,1100b + 00,1100,1110b + 00,0110,0111b = 10,1101,0001b
You may want to check the results with decimal numbers. The initial number was 103, and the final answer is 721, which is 103 × 7.
In conjunction with multiplication is division. For division, numbers are shifted right. Shift right is shown in Figure 22.6. In dividing integer numbers, round-off errors can occur, as can be seen in the figure.
Shift right: (in binary number operations) Operation of moving all digits of a binary number (with a limited number of digits) to the right by one or more places. The leftmost places are then filled with zeros. This implies dividing that number by 10b, 100b, etc. The rightmost digits are moved out and introduce the roundoff error that occurs in division.
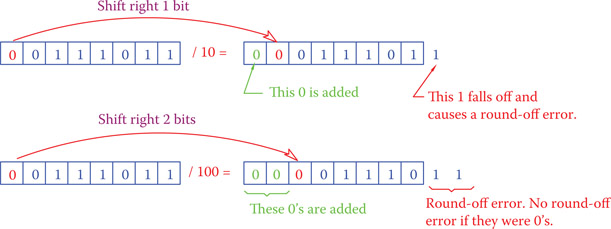
Figure 22.6
Division in binary unsigned numbers.
Example 22.14
Multiply the 12-bit number 0000,0110,1101b by 1011b.
Solution
We see that the multiplier consists 4 bits as follows:
1 × 23 + 1 × 21 + 1 × 20 = 1000b + 10b + 1b
Therefore, the given number must be multiplied by 1000b and 10b and 1, and the results be added together.
For multiplication by 1000b, rotate right 3 bits, for multiplication by 10b, rotate right 1 bit and for multiplication by 1 do not change the number:
| Rotate right 3 bits | 0011,0110,1000 + | |
| Rotate right 1 bit | 0000,1101,1010 |
|
| Add together | 0100,0100,0010 | (iintermediate result) |
| Multiplication by 1 | 0000,,01101101 | |
| Add to the prevvious result | 0100,0100,0010 |
|
| Result | 0100,,10101111 | (210+27 + 25+15 = 1199) |
We can verify the result. The original number is 109 and the multiplier is 11. The result of multiplication must be 109 × 11 = 1199, which is true.
22.5 Number Display and BCD
For digital display of numbers, for example, in a digital watch, a DMM, and many other devices a seven-segment display, matrix display, or other display types are used. In all of these, every digit in a number is handled independent of the other digits. For instance, 216 is not treated as two hundred and sixteen, but as 2, 1, and 6. This is completely acceptable and widely practiced because no mathematical operation is involved in displaying a number.
In displays, all digits are not always needed to be present. In a digital clock, for instance, the leftmost digit must be able to show only 1 (and 2 if a 24 hours format is to be used), and the left digits for minutes and seconds must only show figures 0 to 6; other digits must be able to display 0 to 9. In each particular case, if some unnecessary components can be removed, this is normally done by manufacturers.
For handling numbers 1 and 2 by a binary device, only 2 bits are enough (2 bits can represent four different states or four entities), and for handling 0 to 6 only 3 bits suffice. Three bits can handle up to 8 values (0 to 7). This is one reason for using octal numbers for some practical applications. In a more general case where all digits vary between 0 and 9, 4 bits are necessary for their binary representation. Although up to 16 numbers can be addressed by 4 bits, only 10 of them are utilized (0 to 9) and the rest are unused but are always available. It is clear that for addressing 10 values, 3 bits are definitely not sufficient.
Binary-coded decimal (BCD) refers to treating a decimal number as a set of independent binary numbers corresponding to each individual digit in the number. As an example, the number 192 consists of a 1, a 9, and a 2. It is not before 193 and it is not after 191. Each individual digit, in this way, needs 4 bits to be addressed. For a three-digit decimal number, then, 12 bits are necessary. The binary-coded decimal numbers corresponding to 1, 9, and 2 in 192 are
Binary-coded decimal (BCD): Special representation of decimal values when each individual digit is coded separately in binary form and can be displayed by digital circuits.
0001, 1001, 0010 (1, 9, 2)
Compare the above number with that representing (unsigned) 192, which requires only 8 bits.
192 = 1100,0000b
If we add 8 to 192, the result is 200 = 1100,1000b, but adding 8 to the BCD number has no meaning (0001,1001,1010 BCD has no magnitude content). The binary-coded decimal for 200 is
| 0010, | 0000, | 0000 |
| ↑ | ↑ | ↑ |
| 2 | 0 | 0 |
Example 22.15
Find the BCD number for 1376.
Solution
We need to put the binary equivalents of the digits 1, 3, 7, and 6 together and in the same order.
The answer is
| 0001, | 0011, | 0111, | 0110 |
| ↑ | ↑ | ↑ | ↑ |
| 1 | 3 | 7 | 6 |
22.6 Sampling Analog Variables
In the processes or machinery that are controlled by a microcontroller or microprocessor, as we learned earlier in this chapter, all analog data must be converted to digital, so that it can be represented by binary numbers and be usable by the microprocessor. We learned about precision in converting analog numbers to their digital representation and its relationship with the number of bits.
When a variable entity such as wind speed, car speed, or electric current in a motor is measured, the value obtained is for only the moment the measurement is performed. In a continuous process the measured value is used for one or more necessary actions to be taken. For example, when a car is driven, the position of the gas pedal depressed by the driver is used to adjust car speed.
22.6.1 Sampling
In a continuous process any measurement must be frequently repeated for updated values. Therefore, for microprocessor control of a device another factor comes into picture: the rate at which the data are updated.
This updating of measured values is called sampling and how often a variable is updated is determined by the sampling rate. The sampling rate can also be called sampling frequency, which implies how many times in one second the variable is measured. The time interval between each two measurements is called the sampling time.
Sampling: Action of measuring a variable in a process or machine repeatedly at a fixed frequency, for control purposes.
Sampling rate: Same as the sampling frequency. The (normally fixed) frequency at which a sampling action is performed.
Sampling frequency: The number of samples taken (or measurements made) in 1 second in a sampled data system. This is for converting analog values to digital values for digital control, computer control, display of values, and so on.
Sampling time: Time interval between each two consecutive measurements in a sampling action.
For example, if in each second a variable is measured 1000 times, the sampling rate is 1000 per second, and the sampling time is 0.001 second. Depending on how important a role a parameter has in a process, this updating of values must be performed at a higher sampling rate.
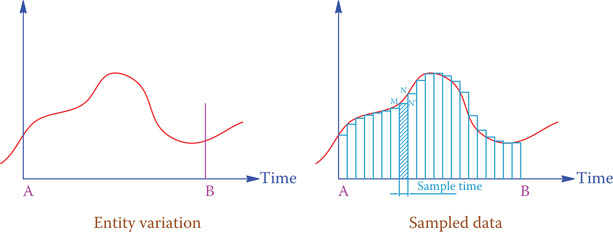
Figure 22.7
Sampling a variable parameter.
In Figure 22.7 a variable is sampled between times A and B. The variable is assumed to remain constant at the measured value for the total period of the sampling time until the next measurement is performed. In reality, it is more likely that the value of a variable changes even if the time interval is very small. For example, the value of the parameter at M is changing to that at N, whereas in the microcontroller it is kept constant until the new reading comes in, which implies a jump from N′ to N. It is thus obvious that more precision in measurement and control can be achieved by having a smaller sampling time. The measured value of any variable is stored by a circuit called sample and hold.
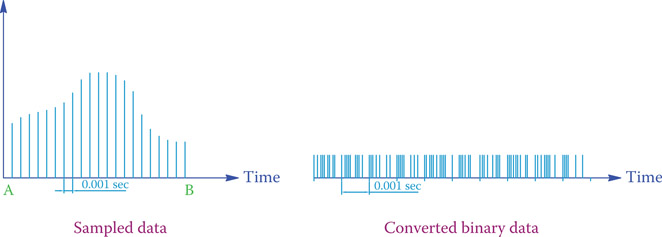
Figure 22.8
Sampled data and their binary conversion.
Sample and hold: Action of measuring a variable and storing the measured value for use. This is common in computer control systems where measurements are performed repeatedly (but not continuously; say at 1 msec intervals) at a proper fixed frequency.
Nowadays, fast sampling, for instance, one million samples per second (a sampling time of 1 microsecond) is possible for many measurements. This implies that the necessary time for measuring the variable under question, converting its value to digital and storing the result can be less than 1 millionth of a second. It must be noted that, in general, the higher the sampling rate is, the higher the price of the sampling equipment.
Increasing the sampling rate is not always necessarily essential, useful, or worth the cost even if possible. For example, consider the pitch angle of a wind turbine. If it takes 1 sec for the pitch angle to change (through its mechanism), any measurement faster than 1 per second does not have any useful effect. Also, if the measurement itself takes a long time, or the process is slow, such as heating a liquid, there is no point in sampling at a high rate. It can only add to the cost.
After sampling is performed at any instant, the measured value is converted to its binary form. This is repeated after each sampling time interval. Figure 22.8 shows a typical example of sampled data and its conversion to binary data (the binary conversion is only for demonstration).
22.6.2 Clock Signal
Each microprocessor has a clock to regulate its operation. Each and every single operation, such as adding two bits of data, is performed with the clock pulse. Each clock pulse is a step for synchronized work of all components (for reading new values, conversions, mathematical operations, etc.) and all operations progress step by step. A clock signal is a square pulse train with a fixed frequency. The clock rate can be decreased, and slower pulse trains be made from it for slower processes.
Figure 22.9 shows the pulse train of the clock signal and two other signals with half and one quarter of the clock frequency. Each pulse has a rising edge, a falling edge, and a level part. A device can be sensitive to the rising edge or the falling edge, and, consequently, its function takes place with that part of a pulse. Some devices are level sensitive.
Rising edge: Same as positive going edge and leading edge in a square waveform.
Falling edge: Edge in a square waveform signal where the voltage drops from a positive value to a negative value (or to zero), as opposed to the rising edge.

Figure 22.9
Representation of fixed frequency pulse signals.
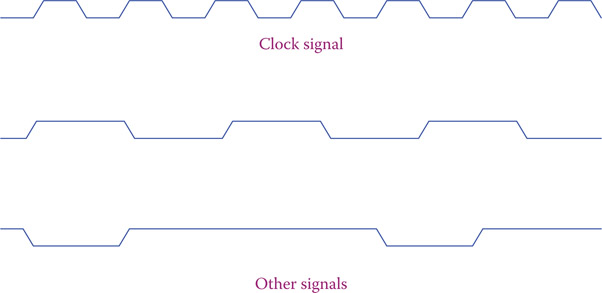
Figure 22.10
Representation of clock and other signals in a microprocessor.
A rising edge is also called a leading edge or positive going edge. A falling edge is also called a trailing edge or a negative going edge. A pulse train continuously switches between zero and a positive value. We refer to these values as low and high.
Leading edge: Same as rising edge in a square waveform.
Positive going edge: Rising edge in a square wave where the magnitude sharply goes positive from negative or zero.
Trailing edge: Same as negative going edge, which is that edge of a rectangular waveform that the value drops from positive to negative or zero.
Negative going edge: Same as falling edge or trailing edge (changing from a positive value to a negative or zero value in a square wave).
Although microprocessors are very fast and their clock frequencies are in the range of MHz (million hertz), the change from a low level to a high level and vice versa is not instant, and, thus the time for switching (duration of the rising edge and falling edge) is not zero. In this sense, the actual clock signal and other signals are represented as shown in Figure 22.10.
22.7 Chapter Summary
- In addition to the decimal number system that we are accustomed to, there are binary, hexadecimal, and octal number systems for use in digital technology.
- The base in decimal numbers is 10, the base for binary, hexadecimal, and octal systems are 2, 16, and 8, respectively.
- In the same way that in the decimal system the symbols for base numbers are from 0 to 9, in the binary, hexadecimal, and octal systems the base numbers are 0 to 1, 0 to 15, and 0 to 7, respectively.
- In the hexadecimal number system for showing numbers 10 to 15 the symbols A, B, C, D, E, and F are used. F is the last base number; the number after that is 1016. After FF is 10016, after FFF is 100016, and so forth.
- The binary number system contains only 0 and 1. The number after 1 is 10b, after 11b is 100b, and so on.
- The octal number system has 8 digits, from 0 to 7. The number after 7 is 108, after 778 is 1008, and after 7778 is 10008, and so on.
- Any single digit in a binary number is called a bit. An ensemble of 8 bits is called a byte, and two bytes make a word.
- In a binary number the leftmost bit is called the most significant bit (MSB) and the rightmost bit is called the least significant bit (LSB).
- A microprocessor is the brain of a digital computer. Customized microprocessors for small control systems are called micro controllers.
- An analog-to-digital converter (ADC or A/D converter) translates an analog value to a digital value.
- A digital value is made out of a finite number of 0’s and 1’s. This finite number is based on the number of bits in a device. For a very simple application it can be 4, but in today’s laptops it is 64 and for larger computers it is at least 128.
- A digital-to-analog converter (DAC or D/A converter) translates a digital value to an analog value.
- In conversion from an analog (measured) value to digital the number of digits is limited by the physical electronic device. The number of digits defines the precision of conversion.
- All positive integer numbers in a computer application are referred to as unsigned numbers.
- All integer numbers (negative and positive) fall in the category of signed numbers.
- One’s complement of a binary number is obtained by changing all 0’s to 1’s and vice versa.
- Two’s complement of a binary number is obtained by adding 1 to the one’s complement of that number.
- In the binary system the negative of a number is represented by its two’s complement.
- In practice, because the number of bits are fixed, the most signifi-cant bit determines if a signed number is positive or negative. A 1 as the MSB signifies a negative number.
- For digital control of a machine or a process the entities that need measurement are sampled at a constant sampling rate. Sampling rate is the frequency of repeated measurement at “sampling time” intervals.
- Any microprocessor or microcontroller works in steps. All mathematical, logical, and conversion operations are performed one step at a time. The steps are synchronized by a clock signal.
- All signals in a microprocessor are in the form of square wave or pulses, where each pulse has a rising edge, a level and a falling edge.
Review Questions
- What are hexadecimal and octal number systems?
- How many basic symbols are there in the binary number system?
- How many base numbers are required for hexadecimal numbers?
- What is the importance of binary numbers?
- What is the use of octal numbers?
- What do LSB and MSB stand for?
- What is a microcontroller?
- What are meant by overflow and flag in microprocessor terminology?
- What does BCD stand for and what does it mean?
- What do DAC and ADC mean?
- What is the difference between signed and unsigned numbers?
- If the most significant bit in a binary number is 1, what does it imply?
- What is meant by two’s complement of a number?
- What is a D/A converter used for?
- What is the result of 1b + 1b?
Problems
- Convert the following unsigned binary numbers to their decimal values:
- 001011110001
- 101011010110
- 001100111011
- 100010110011
- 111100011101
- 100111000110
- 110110010110
- 100000100001
- Find the decimal values of the following signed binary numbers:
- 111000111001
- 100010111010
- 111100011011
- 110001011001
- 100001000011
- Convert all the unsigned numbers given in Problem 1 to their hexadecimal representation.
- Write the unsigned numbers in Problem 1 in their octal equivalents.
- Convert the following numbers to binary. Use 12 digits.
- 18
- 25
- 132
- 1456
- 2333
- 4000
- Write the one’s complement and two’s complement of the following numbers:
- 0001110011
- 0010110111
- 0010100011
- 0000010110
- 0001001101
- 0011001100
- Find the binary numbers for the negative of those in Problem 5.
- Find the octal values of the following decimal numbers:
- 22
- 33
- 65
- 178
- 4355
- Find the decimal values of the following octal numbers:
- 1058
- 2318
- 4278
- 1778
- 77778
- 10008
- 123458
- Write the following numbers in hexadecimal:
- 13
- 198
- 522
- 1292
- 2020
- 10000
- 99999
- Convert the following hexadecimal numbers to decimal:
- 155
- 2A3B
- AABB
- 10001
- CDA00
- 1A5FF
- FFFF
- Convert the numbers in Problem 11 directly from hexadecimal to binary.
- Find the BCD number for the following decimal numbers:
- 16
- 415
- 840
- 2233
- Write the decimal numbers corresponding to the following BCD numbers:
- 1001,0110,0101,1000
- 0001,0011,0001,1001
- If an 8-digit converter is used for a sensor with 2.5 V range, what is the smallest nonzero voltage that can be displayed?
- For measurement in the range of 0 to 10 V, how many bits are necessary to have a minimum resolution (or precision) of 10 mV?
- Add the numbers given in Problem 6. Hint: Add 2 numbers at a time.
