C. Pandu Rangan
Indian Institute of Technology, Madras
6.2Basics of Amortized Analysis
6.3Meldable Priority Queues and Skew Heaps
Meldable Priority Queue Operations•Amortized Cost of Meld Operation
Priority Queue is one of the most extensively studied Abstract Data Types (ADT) due to its fundamental importance in the context of resource managing systems, such as operating systems. Priority Queues work on finite subsets of a totally ordered universal set U. Without any loss of generality we assume that U is simply the set of all non-negative integers. In its simplest form, a Priority Queue supports two operations, namely,
•insert(x, S): update S by adding an arbitrary x ∈ U to S.
•delete-min(S): update S by removing from S the minimum element of S.
We will assume for the sake of simplicity, all the items of S are distinct. Thus, we assume that x ∉ S at the time of calling insert(x, S). This increases the cardinality of S, denoted usually by |S|, by one. The well-known data structure Heaps, provide an elegant and efficient implementation of Priority Queues. In the Heap based implementation, both insert(x, S) and delete-min(S) take O(log n) time where n = |S|.
Several extensions for the basic Priority Queues were proposed and studied in response to the needs arising in several applications. For example, if an operating system maintains a set of jobs, say print requests, in a priority queue, then, always, the jobs with “high priority” are serviced irrespective of when the job was queued up. This might mean some kind of “unfairness” for low priority jobs queued up earlier. In order to straighten up the situation, we may extend priority queue to support delete-max operation and arbitrarily mix delete-min and delete-max operations to avoid any undue stagnation in the queue. Such priority queues are called Double Ended Priority Queues. It is easy to see that Heap is not an appropriate data structure for Double Ended Priority Queues. Several interesting alternatives are available in the literature [1–3]. You may also refer Chapter 8 of this handbook for a comprehensive discussion on these structures.
In another interesting extension, we consider adding an operation called melding. A meld operation takes two disjoint sets, S1 and S2, and produces the set S = S1 ∪ S2. In terms of an implementation, this requirement translates to building a data structure for S, given the data structures of S1 and S2. A Priority Queue with this extension is called a Meldable Priority Queue. Consider a scenario where an operating system maintains two different priority queues for two printers and one of the printers is down with some problem during operation. Meldable Priority Queues naturally model such a situation.
Again, maintaining the set items in Heaps results in very inefficient implementation of Meldable Priority Queues. Specifically, designing a data structure with O(log n) bound for each of the Meldable Priority Queue operations calls for more sophisticated ideas and approaches. An interesting data structure called Leftist Trees, implements all the operations of Meldable Priority Queues in O(log n) time. Leftist Trees are discussed in Chapter 5 of this handbook.
The main objective behind the design of a data structure for an ADT is to implement the ADT operations as efficiently as possible. Typically, efficiency of a structure is judged by its worst-case performance. Thus, when designing a data structure, we seek to minimize the worst case complexity of each operation. While this is a most desirable goal and has been theoretically realized for a number of data structures for key ADTs, the data structures optimizing worst-case costs of ADT operations are often very complex and pretty tedious to implement. Hence, computer scientists were exploring alternative design criteria that would result in simpler structures without losing much in terms of performance. In Chapter 14 of this handbook, we show that incorporating randomness provides an attractive alternative avenue for designers of the data structures. In this chapter we will explore yet another design goal leading to simpler structural alternatives without any degrading in overall performance.
Since the data structures are used as basic building blocks for implementing algorithms, a typical execution of an algorithm might consist of a sequence of operations using the data structure over and again. In the worst case complexity based design, we seek to reduce the cost of each operation as much as possible. While this leads to an overall reduction in the cost for the sequence of operations, this poses some constraints on the designer of data structure. We may relax the requirement that the cost of each operation be minimized and perhaps design data structures that seek to minimize the total cost of any sequence of operations. Thus, in this new kind of design goal, we will not be terribly concerned with the cost of any individual operations, but worry about the total cost of any sequence of operations. At first thinking, this might look like a formidable goal as we are attempting to minimize the cost of an arbitrary mix of ADT operations and it may not even be entirely clear how this design goal could lead to simpler data structures. Well, it is typical of a novel and deep idea; at first attempt it may puzzle and bamboozle the learner and with practice one tends to get a good intuitive grasp of the intricacies of the idea. This is one of those ideas that requires some getting used to. In this chapter, we discuss about a data structure called Skew heaps. For any sequence of a Meldable Priority Queue operations, its total cost on Skew Heaps is asymptotically same as its total cost on Leftist Trees. However, Skew Heaps are a bit simpler than Leftist Trees.
6.2Basics of Amortized Analysis
We will now clarify the subtleties involved in the new design goal with an example. Consider a typical implementation of Dictionary operations. The so called Balanced Binary Search Tree structure (BBST) implements these operations in O(m log n) worst case bound. Thus, the total cost of an arbitrary sequence of m dictionary operations, each performed on a tree of size at most n, will be O(log n). Now we may turn around and ask: Is there a data structure on which the cost of a sequence of m dictionary operations is O(m log n) but individual operations are not constrained to have O(log n) bound? Another more pertinent question to our discussion - Is that structure simpler than BBST, at least in principle? An affirmative answer to both the questions is provided by a data structure called Splay Trees. Splay Tree is the theme of Chapter 13 of this handbook.
Consider for example a sequence of m dictionary operations S1, S2, …, Sm, performed using a BBST. Assume further that the size of the tree has never exceeded n during the sequence of operations. It is also fairly reasonable to assume that we begin with an empty tree and this would imply n ≤ m. Let the actual cost of executing Si be Ci. Then the total cost of the sequence of operations is C1 + C2 + ··· + Cm. Since each Ci is O(log n) we easily conclude that the total cost is O(m log n). No big arithmetic is needed and the analysis is easily finished. Now, assume that we execute the same sequence of m operations but employ a Splay Tree in stead of a BBST. Assuming that ci is the actual cost of Si in a Splay Tree, the total cost for executing the sequence of operation turns out to be c1 + c2 + ··· + cm. This sum, however, is tricky to compute. This is because a wide range of values are possible for each of ci and no upper bound other than the trivial bound of O(n) is available for ci. Thus, a naive, worst case cost analysis would yield only a weak upper bound of O(nm) whereas the actual bound is O(m log n). But how do we arrive at such improved estimates?
This is where we need yet another powerful tool called potential function.
The potential function is purely a conceptual entity and this is introduced only for the sake of computing a sum of widely varying quantities in a convenient way. Suppose there is a function f:D → R+ ∪ {0}, that maps a configuration of the data structure to a non-negative real number. We shall refer to this function as potential function. Since the data type as well as data structures are typically dynamic, an operation may change the configuration of data structure and hence there may be change of potential value due to this change of configuration. Referring back to our sequence of operations S1, S2, …, Sm, let Di−1 denote the configuration of data structure before the executing the operation Si and Di denote the configuration after the execution of Si. The potential difference due to this operation is defined to be the quantity f(Di) − f(Di−1). Let ci denote the actual cost of Si. We will now introduce yet another quantity, ai, defined by
What is the consequence of this definition?
Note that
Let us introduce one more reasonable assumption that f(D0) = f(ϕ) = 0. Since f(D) ≥ 0 for all non empty structures, we obtain,
If we are able to choose cleverly a “good” potential function so that ai’s have tight, uniform bound, then we can evaluate the sum easily and this bounds the actual cost sum . In other words, we circumvent the difficulties posed by wide variations in ci by introducing new quantities ai which have uniform bounds. A very neat idea indeed! However, care must be exercised while defining the potential function. A poor choice of potential function will result in ais whose sum may be a trivial or useless bound for the sum of actual costs. In fact, arriving at the right potential function is an ingenious task, as you will understand by the end of this chapter or by reading the chapter on Splay Trees.
The description of the data structures such as Splay Trees will not look any different from the description of a typical data structures—it comprises of a description of the organization of the primitive data items and a bunch of routines implementing ADT operations. The key difference is that the routines implementing the ADT operations will not be analyzed for their individual worst case complexity. We will only be interested in the the cumulative effect of these routines in an arbitrary sequence of operations. Analyzing the average potential contribution of an operation in an arbitrary sequence of operations is called amortized analysis. In other words, the routines implementing the ADT operations will be analyzed for their amortized cost. Estimating the amortized cost of an operation is rather an intricate task. The major difficulty is in accounting for the wide variations in the costs of an operation performed at different points in an arbitrary sequence of operations. Although our design goal is influenced by the costs of sequence of operations, defining the notion of amortized cost of an operation in terms of the costs of sequences of operations leads one nowhere. As noted before, using a potential function to off set the variations in the actual costs is a neat way of handling the situation.
In the next definition we formalize the notion of amortized cost.
Definition 6.1: (Amortized Cost)
Let A be an ADT with basic operations O = {O1, O2, …, Ok} and let D be a data structure implementing A. Let f be a potential function defined on the configurations of the data structures to non-negative real number. Assume further that f(Φ) = 0. Let D′ denote a configuration we obtain if we perform an operation Ok on a configuration D and let c denote the actual cost of performing Ok on D. Then, the amortized cost of Ok operating on D, denoted as a(Ok, D), is given by
If a(Ok, D) ≤ c′g(n) for all configuration D of size n, then we say that the amortized cost of Ok is O(g(n)).
Theorem 6.1
Let D be a data structure implementing an ADT and let s1, s2, …, sm denote an arbitrary sequence of ADT operations on the data structure starting from an empty structure D0. Let ci denote actual cost of the operation si and Di denote the configuration obtained which si operated on Di−1, for 1 ≤ i ≤ m. Let ai denote the amortized cost of si operating on Di−1 with respect to an arbitrary potential function. Then,
Proof. Since ai is the amortized cost of si working on the configuration Di−1, we have
Therefore,
■
Remark 6.1
The potential function is common to the definition of amortized cost of all the ADT operations. Since holds good for any potential function, a clever choice of the potential function will yield tight upper bound for the sum of actual cost of a sequence of operations.
6.3Meldable Priority Queues and Skew Heaps
Definition 6.2: (Skew Heaps)
A Skew Heap is simply a binary tree. Values are stored in the structure, one per node, satisfying the heap-order property: A value stored at a node is larger than the value stored at its parent, except for the root (as root has no parent).
Remark 6.2
Throughout our discussion, we handle sets with distinct items. Thus a set of n items is represented by a skew heap of n nodes. The minimum of the set is always at the root. On any path starting from the root and descending towards a leaf, the values are in increasing order.
6.3.1Meldable Priority Queue Operations
Recall that a Meldable Priority queue supports three key operations: insert, delete-min and meld. We will first describe the meld operation and then indicate how other two operations can be performed in terms of the meld operation.
Let S1 and S2 be two sets and H1 and H2 be Skew Heaps storing S1 and S2 respectively. Recall that S1 ∩ S2 = ϕ. The meld operation should produce a single Skew Heap storing the values in S1 ∪ S2. The procedure meld (H1, H2) consists of two phases. In the first phase, the two right most paths are merged to obtain a single right most path. This phase is pretty much like the merging algorithm working on sorted sequences. In this phase, the left subtrees of nodes in the right most paths are not disturbed. In the second phase, we simply swap the children of every node on the merged path except for the lowest. This completes the process of melding.
Figures 6.1–6.3 clarify the phases involved in the meld routine.
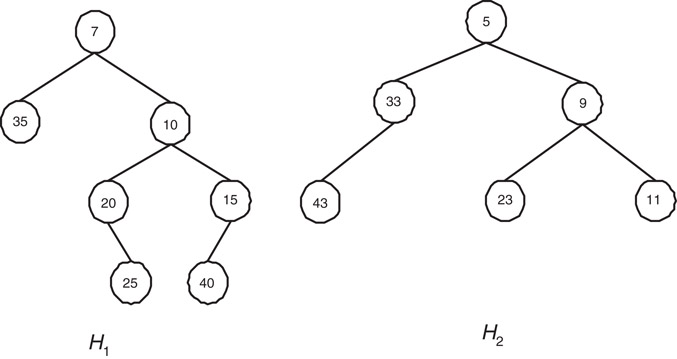
Figure 6.1Skew Heaps for meld operation.
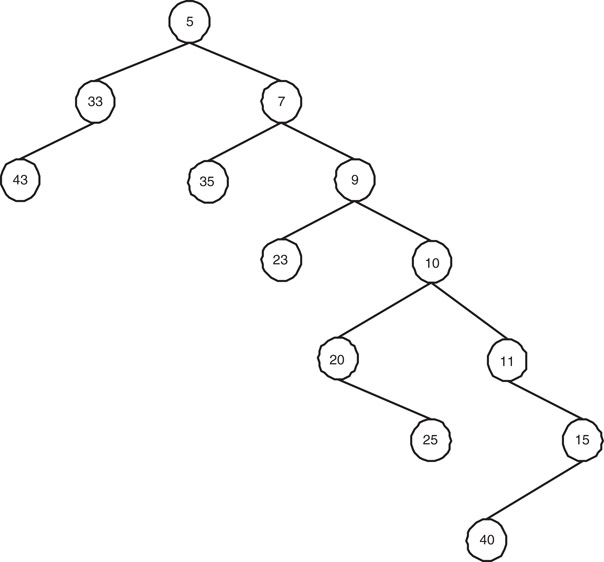
Figure 6.2Rightmost paths are merged. Left subtrees of nodes in the merged path are intact.
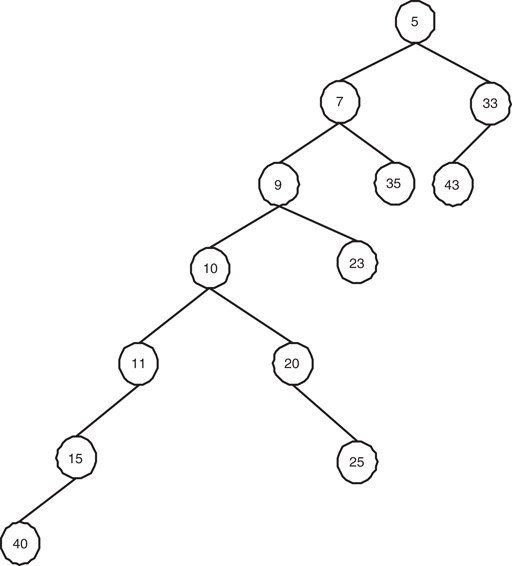
Figure 6.3Left and right children of nodes (5), (7), (9), (10), (11) of Figure 6.2 are swapped. Notice that the children of (15) which is the lowest node in the merged path, are not swapped.
Figure 6.1 shows two Skew Heaps H1 and H2. In Figure 6.2 we have shown the scenario after the completion of the first phase. Notice that right most paths are merged to obtain the right most path of a single tree, keeping the respective left subtrees intact. The final Skew Heap is obtained in Figure 6.3. Note that left and right child of every node on the right most path of the tree in Figure 6.2 (except the lowest) are swapped to obtain the final Skew Heap.
It is easy to implement delete-min and insert in terms of the meld operation. Since minimum is always found at the root, delete-min is done by simply removing the root and melding its left subtree and right subtree. To insert an item x in a Skew Heap H1, we create a Skew Heap H2 consisting of only one node containing x and then meld H1 and H2. From the above discussion, it is clear that cost of meld essentially determines the cost of insert and delete-min. In the next section, we analyze the amortized cost of meld operation.
6.3.2Amortized Cost of Meld Operation
At this juncture we are left with the crucial task of identifying a suitable potential function. Before proceeding further, perhaps one should try the implication of certain simple potential functions and experiment with the resulting amortized cost. For example, you may try the function f(D) = number of nodes in D (and discover how ineffective it is!).
We need some definitions to arrive at our potential function.
Definition 6.3
For any node x in a binary tree, the weight of x, denoted wt(x), is the number of descendants of x, including itself. A non-root node x is said to be heavy if wt(x) > wt(parent(x))/2. A non-root node that is not heavy is called light. The root is neither light nor heavy.
The next lemma is an easy consequence of the definition given above. All logarithms in this section have base 2.
Lemma 6.1
For any node, at most one of its children is heavy. Furthermore, any root to leaf path in a n-node tree contains at most ⌊log n⌋ light nodes.
Definition 6.4: (Potential Function)
A non-root is called right if it is the right child of its parent; it is called left otherwise. The potential of a skew heap is the number of right heavy node it contains. That is, f(H) = number of right heavy nodes in H. We extend the definition of potential function to a collection of skew heaps as follows: .
Here is the key result of this chapter.
Theorem 6.2
Let H1 and H2 be two heaps with n1 and n2 nodes respectively. Let n = n1 + n2. The amortized cost of meld (H1, H2) is O(log n).
Proof. Let h1 and h2 denote the number of heavy nodes in the right most paths of H1 and H2 respectively. The number of light nodes on them will be at most ⌊log n1⌋ and ⌊log n2⌋ respectively. Since a node other than root is either heavy or light, and there are two root nodes here that are neither heavy or light, the total number of nodes in the right most paths is at most
Thus we get a bound for actual cost c as
(6.1) |
|---|
In the process of swapping, the h1 + h2 nodes that were right heavy, will lose their status as right heavy. While they remain heavy, they become left children for their parents hence they do not contribute for the potential of the output tree and this means a drop in potential by h1 + h2. However, the swapping might have created new heavy nodes and let us say, the number of new heavy nodes created in the swapping process is h3. First, observe that all these h3 new nodes are attached to the left most path of the output tree. Secondly, by Lemma 6.1, for each one of these right heavy nodes, its sibling in the left most path is a light node. However, the number of light nodes in the left most path of the output tree is less than or equal to ⌊log n⌋ by Lemma 6.1.
Thus h3 ≤ ⌊log n⌋. Consequently, the net change in the potential is h3 − h1 − h2 ≤ ⌊log n⌋ − h1 − h2.
Hence, the amortized cost of meld operation is O(log n) and this completes the proof. ■
Since insert and delete-min are handled as special cases of meld operation, we conclude
Theorem 6.3
The amortized cost complexity of all the Meldable Priority Queue operations is O(log n) where n is the number of nodes in skew heap or heaps involved in the operation.
Skew Heaps were introduced by Sleator and Tarjan [4]. Leftist Trees have O(log n) worst case complexity for all the Meldable Priority Queue operations but they require heights of each subtree to be maintained as additional information at each node. Skew Heaps are simpler than Leftist Trees in the sense that no additional ‘balancing’ information need to be maintained and the meld operation simply swaps the children of the right most path without any constraints and this results in a simpler code. The bound 3 log2 n + 2 for melding was significantly improved to logϕn (here ϕ denotes the well-known golden ratio which is roughly 1.6) by using a different potential function and an intricate analysis in Reference 5. Recently, this bound was shown to be tight in Reference 6. Pairing Heap, introduced by Fredman et al. [7], is yet another self-adjusting heap structure and its relation to Skew Heaps is explored in Chapter 7 of this handbook.
1.A. Aravind and C. Pandu Rangan, Symmetric Min-Max heaps: A simple data structure for double-ended priority queue, Information Processing Letters, 69:197–199, 1999.
2.S. Carlson, The Deap—A double ended heap to implement a double ended priority queue, Information Processing Letters, 26:33–36, 1987.
3.S. Chang, and M. Du, Diamond dequeue: A simple data structure for priority dequeues, Information Processing Letters, 46:231–237, 1993.
4.D. D. Sleator and R. E. Tarjan, Self-adjusting heaps, Journal on Computing, 15:52–69, 1986.
5.A. Kaldewaij and B. Schoenmakers, The derivation of a tighter bound for top-down skew heaps, Information Processing Letters, 37:265–271, 1991.
6.B. Schoenmakers, A tight lower bound for top-down skew heaps, Information Processing Letters, 61:279–284, 1997.
7.M. L. Fredman, R. Sedgewick, D. D. Sleator, and R. E. Tarjan, The pairing heap: A new form of self-adjusting heap, Algorithmica, 1:111–129, 1986.
*This chapter has been reprinted from first edition of this Handbook, without any content updates.
