Binomial, Fibonacci, and Pairing Heaps
Michael L. Fredman
Rutgers University
Other Variations of Pairing Heaps•Adaptive Properties of Pairing Heaps•Soft Heaps
This chapter presents three algorithmically related data structures for implementing meldable priority queues: binomial heaps, Fibonacci heaps, and pairing heaps. What these three structures have in common is that (a) they are comprised of heap-ordered trees, (b) the comparisons performed to execute extractmin operations exclusively involve keys stored in the roots of trees, and (c) a common side effect of a comparison between two root keys is the linking of the respective roots: one tree becomes a new subtree joined to the other root.
A tree is considered heap-ordered provided that each node contains one item, and the key of the item stored in the parent p(x) of a node x never exceeds the key of the item stored in x. Thus when two roots get linked, the root storing the larger key becomes a child of the other root. By convention, a linking operation positions the new child of a node as its leftmost child. Figure 7.1 illustrates these notions.
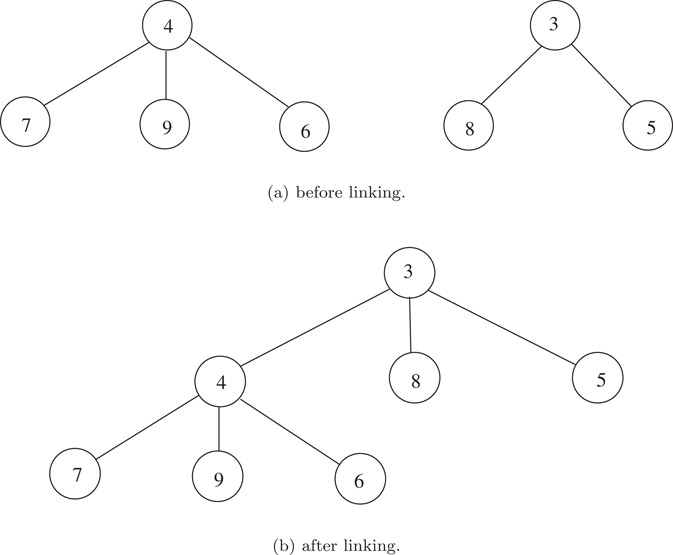
Figure 7.1Two heap-ordered trees and the result of their linking: (a) before linking and (b) after linking.
Of the three data structures, the binomial heap structure was the first to be invented [1], designed to efficiently support the operations: insert, extractmin, delete, and meld. The binomial heap has been highly appreciated as an elegant and conceptually simple data structure, particularly given its ability to support the meld operation. The Fibonacci heap data structure [2] was inspired by and can be viewed as a generalization of the binomial heap structure. The raison d’être of the Fibonacci heap structure is its ability to efficiently execute decrease-key operations. A decrease-key operation replaces the key of an item, specified by location, by a smaller value, for example, decrease-key(P,knew,H). (The arguments specify that the item is located in node P of the priority queue H and that its new key value is knew.) Decrease-key operations are prevalent in many network optimization algorithms, including minimum spanning tree and shortest path. The pairing heap data structure [3] was devised as a self-adjusting analogue of the Fibonacci heap and has proved to be more efficient in practice [4].
Binomial heaps and Fibonacci heaps are primarily of theoretical and historical interest. The pairing heap is the more efficient and versatile data structure from a practical standpoint. The following three sections describe the respective data structures.
We begin with an informal overview. A single binomial heap structure consists of a forest of specially structured trees, referred to as binomial trees. The number of nodes in a binomial tree is always a power of two. Defined recursively, the binomial tree B0 consists of a single node. The binomial tree Bk, for k > 0, is obtained by linking two trees Bk − 1 together: one tree becomes the leftmost subtree of the other. In general, Bk has 2k nodes. Figures 7.2a and b illustrate the recursion and show several trees in the series. An alternative and useful way to view the structure of Bk is depicted in Figure 7.2c: Bk consists of a root and subtrees (in order from left to right) Bk − 1, Bk − 2,…, B0. The root of the binomial tree Bk has k children, and the tree is said to have rank k. We also observe that the height of Bk (maximum number of edges on any path directed away from the root) is k. The name “binomial heap” is inspired by the fact that the root of Bk has descendants at distance j.

Figure 7.2Binomial trees and their recursions: (a) recursion for binomial trees, (b) several binomial trees, and (c) an alternative recursion.
Because binomial trees have restricted sizes, a forest of trees is required to represent a priority queue of arbitrary size. A key observation, indeed a motivation for having tree sizes being powers of two, is that a priority queue of arbitrary size can be represented as a union of trees of distinct sizes. (In fact, the sizes of the constituent trees are uniquely determined and correspond to the powers of two that define the binary expansion of n, the size of the priority queue.) Moreover, because the tree sizes are unique, the number of trees in the forest of a priority queue of size n is at most . Thus finding the minimum key in the priority queue, which clearly lies in the root of one of its constituent trees (due to the heap-order condition), requires searching among at most tree roots. Figure 7.3 gives an example of binomial heap.

Figure 7.3A binomial heap (showing placement of keys among forest nodes).
Now let’s consider, from a high-level perspective, how the various heap operations are performed. As with leftist heaps (cf. Chapter 5), the various priority queue operations are to a large extent comprised of melding operations, and so we consider first the melding of two heaps.
The melding of two heaps proceeds as follows: (a) the trees of the respective forests are combined into a single forest and then (b) consolidation takes place: pairs of trees having common rank are linked together until all remaining trees have distinct ranks. Figure 7.4 illustrates the process. An actual implementation mimics binary addition and proceeds in much the same was as merging two sorted lists in ascending order. We note that insertion is a special case of melding.
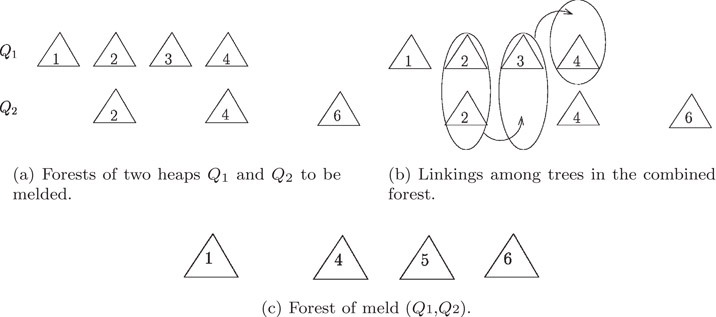
Figure 7.4Melding of two binomial heaps. The encircled objects reflect trees of common rank being linked. (Ranks are shown as numerals positioned within triangles which in turn represent individual trees.) Once linking takes place, the resulting tree becomes eligible for participation in further linkings, as indicated by the arrows that identify these linking results with participants of other linkings. (a) Forests of two heaps Q1 and Q2 to be melded. (b) Linkings among trees in the combined forest. (c) Forest of meld (Q1, Q2).
The extractmin operation is performed in two stages. First, the minimum root, the node containing the minimum key in the data structure, is found by examining the tree roots of the appropriate forest, and this node is removed. Next, the forest consisting of the subtrees of this removed root, whose ranks are distinct (see Figure 7.2c) and thus viewable as constituting a binomial heap, is melded with the forest consisting of the trees that remain from the original forest. Figure 7.5 illustrates the process.

Figure 7.5Extractmin operation: The location of the minimum key is indicated in (a). The two encircled sets of trees shown in (b) represent forests to be melded. The smaller trees were initially subtrees of the root of the tree referenced in (a).
Finally, we consider arbitrary deletion. We assume that the node ν containing the item to be deleted is specified. Proceeding up the path to the root of the tree containing ν, we permute the items among the nodes on this path, placing in the root the item x originally in ν, and shifting each of the other items down one position (away from the root) along the path. This is accomplished through a sequence of exchange operations that move x towards the root. The process is referred to as a sift-up operation. Upon reaching the root r, r is then removed from the forest as though an extractmin operation is underway. Observe that the repositioning of items in the ancestors of ν serves to maintain the heap-order property among the remaining nodes of the forest. Figure 7.6 illustrates the repositioning of the item being deleted to the root.

Figure 7.6Initial phase of deletion—sift-up operation: (a) initial item placement and (b) after movement to root.
This completes our high-level descriptions of the heap operations. For navigational purposes, each node contains a leftmost child pointer and a sibling pointer that points to the next sibling to its right. The children of a node are thus stored in the linked list defined by sibling pointers among these children, and the head of this list can be accessed by the leftmost child pointer of the parent. This provides the required access to the children of a node for the purpose of implementing extractmin operations. Note that when a node obtains a new child as a consequence of a linking operation, the new child is positioned at the head of its list of siblings. To facilitate arbitrary deletions, we need a third pointer in each node pointing to its parent. To facilitate access to the ranks of trees, we maintain in each node the number of children it has, and refer to this quantity as the node rank. Node ranks are readily maintained under linking operations; the node rank of the root gaining a child gets incremented. Figure 7.7 depicts these structural features.

Figure 7.7Structure associated with a binomial heap node: (a) fields of a node and (b) a node and its three children.
As seen in Figure 7.2c, the ranks of the children of a node form a descending sequence in the children’s linked list. However, since the melding operation is implemented by accessing the tree roots in ascending rank order, when deleting a root we first reverse the list order of its children before proceeding with the melding.
Each of the priority queue operations requires in the worst case O(log n) time, where n is the size of the heap that results from the operation. This follows, for melding, from the fact that its execution time is proportional to the combined lengths of the forest lists being merged. For extractmin, this follows from the time for melding, along with the fact that a root node has only O(log n) children. For arbitrary deletion, the time required for the sift-up operation is bounded by an amount proportional to the height of the tree containing the item. Including the time required for extractmin, it follows that the time required for arbitrary deletion is O(log n).
A detailed code for manipulating binomial heaps can be found in Weiss [5].
Fibonacci heaps were specifically designed to efficiently support decrease-key operations. For this purpose, the binomial heap can be regarded as a natural starting point. Why? Consider the class of priority queue data structures that are implemented as forests of heap-ordered trees, as will be the case for Fibonacci heaps. One way to immediately execute a decrease-key operation, remaining within the framework of heap-ordered forests, is to simply change the key of the specified data item and sever its link to its parent, inserting the severed subtree as a new tree in the forest. Figure 7.8 illustrates the process. (Observe that the link to the parent only needs to be cut if the new key value is smaller than the key in the parent node, violating heap order.) Fibonacci heaps accomplish this without degrading the asymptotic efficiency with which other priority queue operations can be supported. Observe that to accommodate node cuts, the list of children of a node needs to be doubly linked. Hence, the nodes of a Fibonacci heap require two sibling pointers.

Figure 7.8Immediate decrease-key operation. The subtree severing (b and c) is necessary only when k′< j. (a) Initial tree. (b) Subtree to be severed. (c) Resulting changes.
Fibonacci heaps support findmin, insertion, meld, and decrease-key operations in constant amortized time, and deletion operations in O(log n) amortized time. For many applications, the distinction between worst-case times versus amortized times is of little significance. A Fibonacci heap consists of a forest of heap-ordered trees. As we shall see, Fibonacci heaps differ from binomial heaps in that there may be many trees in a forest of the same rank, and there is no constraint on the ordering of the trees in the forest list. The heap also includes a pointer to the tree root containing the minimum item, referred to as the min-pointer, that facilitates findmin operations. Figure 7.9 provides an example of a Fibonacci heap and illustrates certain structural aspects.
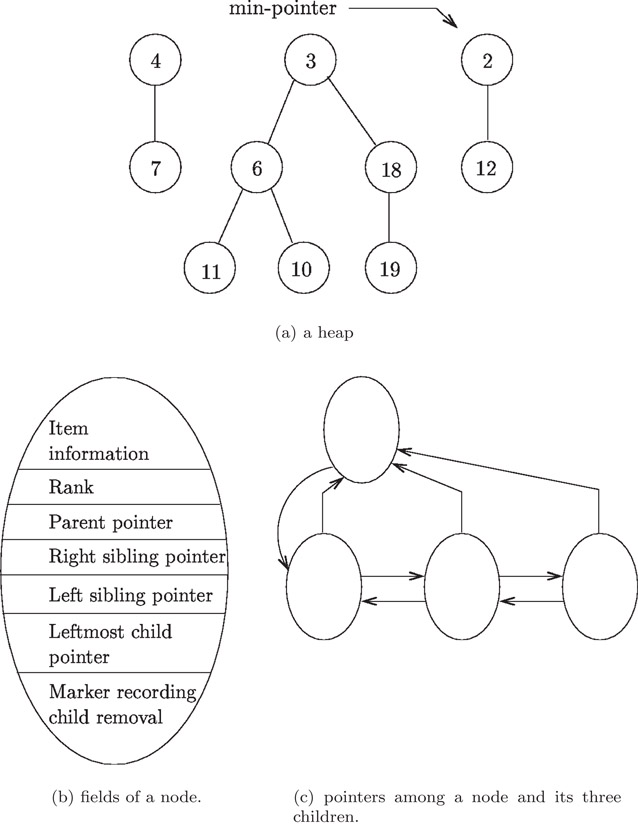
Figure 7.9A Fibonacci heap and associated structure: (a) a heap, (b) fields of a node, and (c) pointers among a node and its three children.
The impact of severing subtrees is clearly incompatible with the pristine structure of the binomial tree that is the hallmark of the binomial heap. Nevertheless, the tree structures that can appear in the Fibonacci heap data structure must sufficiently approximate binomial trees in order to satisfy the performance bounds we seek. The linking constraint imposed by binomial heaps, that trees being linked must have the same size, ensures that the number of children a node has (its rank), grows no faster than the logarithm of the size of the subtree rooted at the node. This rank versus subtree size relation is the key to obtaining the O(log n) deletion time bound. Fibonacci heap manipulations are designed with this in mind.
Fibonacci heaps utilize a protocol referred to as cascading cuts to enforce the required rank versus subtree size relation. Once a node ν has had two of its children removed as a result of cuts, ν’s contribution to the rank of its parent is then considered suspect in terms of rank versus subtree size. The cascading cut protocol requires that the link to ν’s parent be cut, with the subtree rooted at ν then being inserted into the forest as a new tree. If ν’s parent has, as a result, had a second child removed, then it in turn needs to be cut, and the cuts may thus cascade. Cascading cuts ensure that no nonroot node has had more than one child removed subsequent to being linked to its parent.
We keep track of the removal of children by marking a node if one of its children has been cut. A marked node that has another child removed is then subject to being cut from its parent. When a marked node becomes linked as a child to another node, or when it gets cut from its parent, it gets unmarked. Figure 7.10 illustrates the protocol of cascading cuts.

Figure 7.10Illustration of cascading cuts. In (b), the dashed lines reflect cuts that have taken place, two nodes marked in (a) get unmarked, and a third node gets marked. (a) Before decrease-key, (b) after decrease-key.
Now the induced node cuts under the cascading cuts protocol, in contrast with those primary cuts immediately triggered by decrease-key operations, are bounded in number by the number of primary cuts. (This follows from consideration of a potential function defined to be the total number of marked nodes.) Therefore, the burden imposed by cascading cuts can be viewed as effectively only doubling the number of cuts taking place in the absence of the protocol. One can therefore expect that the performance asymptotics are not degraded as a consequence of proliferating cuts. As with binomial heaps, two trees in a Fibonacci heap can only be linked if they have equal rank. With the cascading cuts protocol in place, we claim that the required rank versus subtree size relation holds, a matter which we address next.
Let’s consider how small the subtree rooted at a node ν having rank k can be. Let ω be the mth child of ν from the right. At the time it was linked to ν, ν had at least m − 1 other children (those currently to the right of ω were certainly present). Therefore, ω had rank at least m − 1 when it was linked to ν. Under the cascading cuts protocol, the rank of ω could have decreased by at most one after its linking to ν; otherwise it would have been removed as a child. Therefore, the current rank of ω is at least m − 2. We minimize the size of the subtree rooted at ν by minimizing the sizes (and ranks) of the subtrees rooted at ν’s children. Now let Fj be the minimum possible size of the subtree rooted at a node of rank j, so that the size of the subtree rooted at ν is Fk. We conclude that (for k ≥ 2)
where the final term, 1, reflects the contribution of ν to the subtree size. Clearly, F0 = 1 and F1 = 2. See Figure 7.11 for an illustration of this construction. Based on the preceding recurrence, it is readily shown that Fk is given by the (k + 2)th Fibonacci number (from whence the name “Fibonacci heap” was inspired). Moreover, since the Fibonacci numbers grow exponentially fast, we conclude that the rank of a node is indeed bounded by the logarithm of the size of the subtree rooted at the node.

Figure 7.11Minimal tree of rank k. Node ranks are shown adjacent to each node.
We proceed next to describe how the various operations are performed.
Since we are not seeking worst-case bounds, there are economies to be exploited that could also be applied to obtain a variant of Binomial heaps. (In the absence of cuts, the individual trees generated by Fibonacci heap manipulations would all be binomial trees.) In particular, we shall adopt a lazy approach to melding operations: the respective forests are simply combined by concatenating their tree lists and retaining the appropriate min-pointer. This requires only constant time.
An item is deleted from a Fibonacci heap by deleting the node that originally contains it, in contrast with Binomial heaps. This is accomplished by (a) cutting the link to the node’s parent (as in decrease-key) if the node is not a tree root and (b) appending the list of children of the node to the forest. Now if the deleted node happens to be referenced by the min-pointer, considerable work is required to restore the min-pointer—the work previously deferred by the lazy approach to the operations. In the course of searching among the roots of the forest to discover the new minimum key, we also link trees together in a consolidation process.
Consolidation processes the trees in the forest, linking them in pairs until there are no longer two trees having the same rank, and then places the remaining trees in a new forest list (naturally extending the melding process employed by binomial heaps). This can be accomplished in time proportional to the number of trees in forest plus the maximum possible node rank. Let max-rank denotes the maximum possible node rank. (The preceding discussion implies that max-rank = O(logheap-size).) Consolidation is initialized by setting up an array A of trees (initially empty) indexed by the range [0,max-rank]. A nonempty position A[d] of A contains a tree of rank d. The trees of the forest are then processed using the array A as follows. To process a tree T of rank d, we insert T into A[d] if this position of A is empty, completing the processing of T. However, if A[d] already contains a tree U, then T and U are linked together to form a tree W, and the processing continues as before, but with W in place of T, until eventually an empty location of A is accessed, completing the processing associated with T. After all of the trees have been processed in this manner, the array A is scanned, placing each of its stored trees in a new forest. Apart from the final scanning step, the total time necessary to consolidate a forest is proportional to its number of trees, since the total number of tree pairings that can take place is bounded by this number (each pairing reduces by one the total number of trees present). The time required for the final scanning step is given by max-rank = log(heap-size).
The amortized timing analysis of Fibonacci heaps considers a potential function defined as the total number of trees in the forests of the various heaps being maintained. Ignoring consolidation, each operation takes constant actual time, apart from an amount of time proportional to the number of subtree cuts due to cascading (which, as noted above, is only constant in amortized terms). These cuts also contribute to the potential. The children of a deleted node increase the potential by O(logheap-size). Deletion of a minimum heap node additionally incurs the cost of consolidation. However, consolidation reduces our potential, so that the amortized time it requires is only O(logheap-size). We conclude therefore that all nondeletion operations require constant amortized time, and deletion requires O(log n) amortized time.
An interesting and unresolved issue concerns the protocol of cascading cuts. How would the performance of Fibonacci heaps be affected by the absence of this protocol?
A detailed code for manipulating Fibonacci heaps can be found in Knuth [6].
The pairing heap was designed to be a self-adjusting analogue of the Fibonacci heap, in much the same way that the skew heap is a self-adjusting analogue of the leftist heap (see Chapters 5 and 6). The only structure maintained in a pairing heap node, besides item information, consists of three pointers: leftmost child and two sibling pointers. (The leftmost child of a node uses its left sibling pointer to point to its parent, to facilitate updating the leftmost child pointer its parent.) See Figure 7.12 for an illustration of pointer structure.

Figure 7.12Pointers among a pairing heap node and its three children.
There are no cascading cuts—only simple cuts for decrease-key and deletion operations. With the absence of parent pointers, decrease-key operations uniformly require a single cut (removal from the sibling list, in actuality), as there is no efficient way to check whether heap order would otherwise be violated. Although there are several varieties of pairing heaps, our discussion presents the two-pass version (the simplest), for which a given heap consists of only a single tree. The minimum element is thus uniquely located, and melding requires only a single linking operation. Similarly, a decrease-key operation consists of a subtree cut followed by a linking operation. Extractmin is implemented by removing the tree root and then linking the root’s subtrees in a manner described later. Other deletions involve (a) a subtree cut, (b) an extractmin operation on the cut subtree, and (c) linking the remnant of the cut subtree with the original root.
The extractmin operation combines the subtrees of the root using a process referred to as two-pass pairing. Let x1,…, xk be the subtrees of the root in left-to-right order. The first pass begins by linking x1 and x2. Then x3 and x4 are linked, followed by x5 and x6, and so on, so that the odd positioned trees are linked with neighboring even positioned trees. Let y1,…, yh, h = ⌈k/2⌉, be the resulting trees, respecting left-to-right order. (If k is odd, then y⌈k/2⌉ is xk.) The second pass reduces these to a single tree with linkings that proceed from right-to-left. The rightmost pair of trees, yh and yh − 1 are linked first, followed by the linking of yh − 2 with the result of the preceding linking, and so on, until finally we link y1 with the structure formed from the linkings of y2,…, yh (see Figure 7.13).

Figure 7.13Two-pass pairing. The encircled trees get linked. For example, in (b) trees A and B get linked, and the result then gets linked with the tree C, and so on: (a) first pass, (b) second pass.
Since two-pass pairing is not particularly intuitive, a few motivating remarks are offered. The first pass is natural enough, and one might consider simply repeating the process on the remaining trees, until, after logarithmically many such passes, only one tree remains. Indeed, this is known as the multipass variation. Unfortunately, its behavior is less understood than that of the two-pass pairing variation.
The second (right-to-left) pass is also quite natural. Let H be a binomial heap with exactly 2k items, so that it consists of a single tree. Now suppose that an extractmin followed by an insertion operation are executed. The linkings that take place among the subtrees of the deleted root (after the new node is linked with the rightmost of these subtrees) entail the right-to-left processing that characterizes the second pass. So why not simply rely upon a single right-to-left pass and omit the first? The reason is that although the second pass preserves existing balance within the structure, it doesn’t improve upon poorly balanced situations (manifested when most linkings take place between trees of disparate sizes). For example, using a single-right-to-left-pass version of a pairing heap to sort an increasing sequence of length n (n insertions followed by n extractmin operations) would result in an n2 sorting algorithm. (Each of the extractmin operations yields a tree of height 1 or less.) See Section 7.5, however, for an interesting twist.
In actuality two-pass pairing was inspired [3] by consideration of splay trees (see Chapter 13). If we consider the child, sibling representation that maps a forest of arbitrary trees into a binary tree, then two-pass pairing can be viewed as a splay operation on a search tree path with no bends [3]. The analysis for splay trees then carries over to provide an amortized analysis for pairing heaps.
A detailed code for manipulating pairing heaps can be found in Weiss [5].
The asymptotic behavior of pairing heaps is an interesting and unresolved matter. In the original paper [3], it was demonstrated that the operations require only O(log n) amortized time. The fact that decrease-key operations require only constant actual time makes seemingly plausible the possibility that the amortized costs of the various operations match those of Fibonacci heaps. This line of thought, however, requires addressing the possibility that the presence of decrease-key operations might degrade the efficiency with which extractmin operations can be performed. On the positive side, Pettie [7] has derived a amortized bound for decrease-key and insertion operations (in the presence of a O(log n) bound for the extractmin operation), and it is known that for those applications for which decrease-key operations are highly predominant, pairing heaps provably meet the optimal asymptotic bounds characteristic of Fibonacci heaps [8].
Despite the above positive considerations, as a theoretical matter pairing heaps do not match the asymptotic bounds of Fibonacci heaps. More precisely, it has been demonstrated [8] that there exist operation sequences for which the aggregate execution cost via pairing heaps is not consistent with amortized costs of O(log n) for extractmin and insertion operations, and O(log log n) for decrease-key operations. (We observe that Pettie’s upper bound [7] on the amortized cost of decrease-key operations, cited above, exceeds any fixed power of log log n.) The derivation of this negative result takes place in an information-theoretic framework, so that it is applicable to all data structures encompassed in a suitably defined model of computation, a matter that we shall return to shortly.
In terms of practice, because the pairing heap design dispenses with the rather complicated, carefully crafted constructs put in place primarily to facilitate proving the time bounds enjoyed by Fibonacci heaps, we can expect efficiency gains at the level of elementary steps such as linking operations. The study of Moret and Shapiro [4] provides experimental evidence in support of the conclusion that pairing heaps are superior to Fibonacci heaps in practice.
7.5.1Other Variations of Pairing Heaps
The reader may wonder whether some alternative to two-pass pairing might provably attain the asymptotic performance bounds satisfied by Fibonacci heaps. The strongest result to date is attained by a variation of pairing heap devised by Elmasry [9], for which extractmin is supported with O(log n) amortized cost and decrease-key with O(log log n) amortized cost (and insertion with O(1) amortized cost), thereby matching the known lower bound applicable for two-pass pairing heaps. The information-theoretic framework [8] under which these lower bounds for two-pass pairing heaps have been established, however, does not encompass structures such as Elmasry’s, so there remains the possibility that some other alternative to two-pass pairing might further improve the upper bounds attained by Elmasry’s structure. We mention that Iacono and Özkan [10] have extended the reach of this information-theoretic framework, developing a “Pure Heap Model” that broadens the class of data structures to which the lower bounds established for two-pass pairing apply. The pure heap model, however, does not encompass Elmasry’s data structure, and moreover the Elmasry upper bounds (matching the lower bounds established for two-pass pairing) have not been demonstrated for any data structure in the pure heap model, though one data structure, the “sort heap” [11], comes close.
7.5.2Adaptive Properties of Pairing Heaps
Consider the problem of merging k sorted lists of respective lengths n1, n2,…, nk, with . The standard merging strategy that performs rounds of pairwise list merges requires time. However, a merge pattern based upon the binary Huffman tree, having minimal external path length for the weights n1, n2,…, nk, is more efficient when the lengths ni are nonuniform and provides a near-optimal solution. Pairing heaps can be utilized to provide a rather different solution as follows. Treat each sorted list as a linearly structured pairing heap. Then (a) meld these k heaps together and (b) repeatedly execute extractmin operations to retrieve the n items in their sorted order. The number of comparisons that take place is bounded by
Since the above multinomial coefficient represents the number of possible merge patterns, the information-theoretic bound implies that this result is optimal to within a constant factor. The pairing heap thus self-organizes the sorted list arrangement to approximate an optimal merge pattern. Iacono has derived a “working-set” theorem that quantifies a similar adaptive property satisfied by pairing heaps. Given a sequence of insertion and extractmin operations initiated with an empty heap, at the time a given item x is deleted we can attribute to x a contribution bounded by O(log op(x)) to the total running time of the sequence, where op(x) is the number of heap operations that have taken place since x was inserted (see Reference 12 for a slightly tighter estimate).
An interesting development [13] that builds upon and extends binomial heaps in a different direction is a data structure referred to as a soft heap. The soft heap departs from the standard notion of priority queue by allowing for a type of error, referred to as corruption, which confers enhanced efficiency. When an item becomes corrupted, its key value gets increased. Findmin returns the minimum current key, which might or might not be corrupted. The user has no control over which items become corrupted, this prerogative belonging to the data structure. But the user does control the overall amount of corruption in the following sense.
The user specifies a parameter, 0 < ε ≤ 1/2, referred to as the error rate, that governs the behavior of the data structure as follows. The operations findmin and deletion are supported in constant amortized time, and insertion is supported in O(log 1/ε) amortized time. Moreover, no more than an ε fraction of the items present in the heap are corrupted at any given time.
To illustrate the concept, let x be an item returned by findmin, from a soft heap of size n. Then there are no more than εn items in the heap whose original keys are less than the original key of x.
Soft heaps are rather subtle, and we won’t attempt to discuss specifics of their design. Soft heaps have been used to construct an optimal comparison-based minimum spanning tree algorithm [14], although its actual running time has not been determined. Soft heaps have also been used to construct a comparison-based algorithm with known running time mα(m, n) on a graph with n vertices and m edges [15], where α(m, n) is a functional inverse of the Ackermann function. Chazelle [13] has also observed that soft heaps can be used to implement median selection in linear time, a significant departure from previous methods.
1.J. Vuillemin, A Data Structure for Manipulating Priority Queues, Communications of the ACM, 21, 1978, 309–314.
2.M. L. Fredman and R. E. Tarjan, Fibonacci Heaps and Their Uses in Improved Optimization Algorithms, Journal of the ACM, 34, 1987, 596–615.
3.M. L. Fredman, R. Sedgewick, D. D. Sleator, and R. E. Tarjan, The Pairing Heap: A New Form of Self-adjusting Heap, Algorithmica, 1, 1986, 111–129.
4.B. M. E. Moret and H. D. Shapiro, An Empirical Analysis of Algorithms for Constructing a Minimum Spanning Tree, Proceedings of the Second Workshop on Algorithms and Data Structures, 1991, 400–411.
5.M. A. Weiss, Data Structures and Algorithms in C, 2nd ed., Addison-Wesley, Reading, MA, 1997.
6.D. E. Knuth, The Stanford Graph Base. ACM Press, New York, NY, 1994.
7.S. Pettie, Towards a Final Analysis of Pairing Heaps, FOCS, 2005, 2005, 174–183.
8.M. L. Fredman, On the Efficiency of Pairing Heaps and Related Data Structures, Journal of the ACM, 46, 1999, 473–501.
9.A. Elmasry, Pairing Heaps with O(log log n) Decrease Cost, SODA, 2009, 471–476.
10.J. Iacono and O. Özkan, A Tight Lower Bound for Decrease-key in the Pure Heap Model. CoRR abs/1407.6665, 2014.
11.J. Iacono and O. Özkan, Why Some Heaps Support Constant-Amortized-Time Decrease-key Operations, and Others Do not, ICALP, (1), 2014, 637–649.
12.J. Iacono, Distribution sensitive data structures, PhD Thesis, Rutgers University, 2001.
13.B. Chazelle, The Soft Heap: An Approximate Priority Queue with Optimal Error Rate, Journal of the ACM, 47, 2000, 1012–1027.
14.S. Pettie and V. Ramachandran, An Optimal Minimum Spanning Tree Algorithm, Journal of the ACM, 49, 2002, 16–34.
15.B. Chazelle, A Faster Deterministic Algorithm for Minimum Spanning Trees, Journal of the ACM, 47, 2000, 1028–1047.
